基于主从博弈的多微电网储能容量优化配置

王 涛，钟 浩，李世春，张小兵，陈梓桐

（三峡大学梯级水电站运行与控制湖北省重点实验室，湖北宜昌 443002）

0 引言

随着分布式发电技术的发展，微电网[1]逐渐受到了学者们的关注，成为电力系统的研究热点。储能作为微电网内部的关键元件，可以调节微电网的负荷需求。在负荷低谷时期，存储风光机组发出的多余电能；在负荷高峰时期，释放存储的电能，缓解并网后对配电网的冲击，提升微电网的收益[2-5]。但是微电网储能容量过小，会导致微电网的收益有限，甚至会影响微电网内部的供电可靠性；微电网储能容量过大，则会使得自身投资及运维成本过高，并网后增大配电网的网损电量，导致配电网的运行成本增加[6-9]。因此，合理配置微电网储能容量，对提升储能充放电的协调性具有重要研究意义。

目前，对于微电网储能的配置问题，国内外已有大量相关研究。文献[10-13]针对离网型微电网，以微电网经济性和可靠性等指标作为优化目标，对储能容量进行优化。文献[14]以并网型微电网为研究对象，以微电网自身经济性和供电可靠性为目标优化储能容量。文献[15]以配电网的电能质量和经济性作为目标函数，对微电网进行多目标优化配置。文献[16]提出了一种考虑微电网内多类型需求响应资源可柔性调节区间的储能容量优化配置模型。文献[10-16]仅考虑了微电网或配电网单方的利益需求，文献[17]采用纳什议价理论的合作博弈方法，同时考虑微电网群的利益和群内单个微电网的利益，得出最优纳什议价方案。文献[18]建立了多微电网系统、微电网聚合商、各微电网之间的双层协调优化调度模型，使三方收益均得到提高。文献[19]同时考虑了微电网和配电网的利益，在固定电价下，对微电网的储能容量进行优化，使微电网和配电网的成本最低。文献[20]构建了微电网发电侧、用户侧、配电网之间的非合作博弈模型，可以同时满足微电网、配电网和用户侧三方收益最大化的需求。

为了充分发挥价格杠杆在多微电网储能配置中的作用，提升微电网储能充放电的协调性，本文在微电网储能规划阶段，兼顾微电网和配电网运行经济性，以电价为杠杆，建立配电网和多微电网之间的主从博弈模型，对多微电网的储能容量进行优化配置。通过IEEE 33 节点系统算例表明，本文提出的优化配置方案对于多微电网和配电网的经济性均有所提升。

1 多微电网与配电网的主从博弈框架

多微电网与配电网构成主从博弈结构，博弈主体为配电网，博弈从体为多微电网。具体博弈框架如图1 所示。

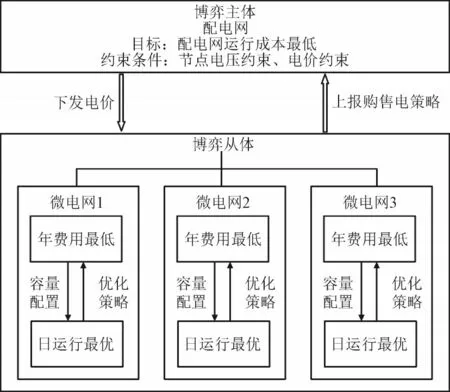
图1 多微电网与配电网的主从博弈框架图Fig.1 Framework diagram of master-slave game between multi-microgrid and distribution network

配电网有制定电价的权力，向多微电网下发电价；多微电网对电价做出响应，考虑运行策略对容量配置的影响，以经济性最优为目标，构建储能容量双层优化配置模型，上层确定储能容量，下层确定微电网运行策略。多微电网将运行策略返回给配电网，配电网基于自身的运行成本对电价进行调整，再次下发给多微电网，循环迭代，直至多微电网和配电网双方达到纳什均衡[21]，输出最优储能容量。本文通过价格杠杆进行多微电网储能容量的优化配置，采用的电价机制为峰谷制电价[22-23]。

2 模型构建

2.1 配电网模型

2.1.1 目标函数

配电网层以配电网年运行成本最低minWT为目标函数，即：

式中:Wloss为配电网年网损成本；Wex为配电网年购售电成本。

其中，

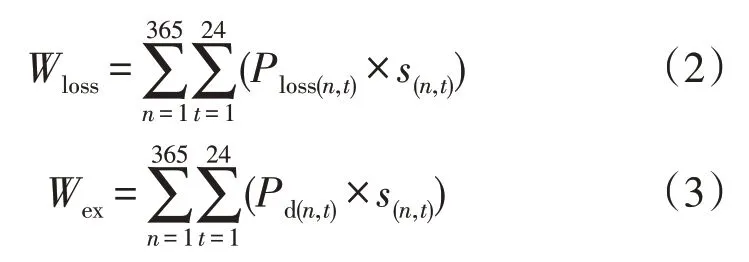
式中：n为天数；t为时刻；Ploss(n,t)为配电网第n天各时刻的有功网损电量；Pd(n,t)为配电网第n天各时刻的购售电功率；s(n,t)为第n天各时刻的电价。

2.1.2 约束条件

1）节点电压约束。即：

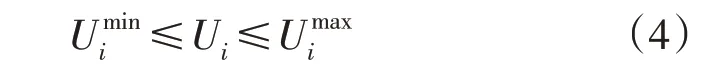
式中：Ui为配电网系统节点中i的电压；分别为配电网系统中节点i电压的最小值和最大值。

2）电价约束。由于微电网和配电网各自是独立的利益主体，需要保证双方的收益。因此，需要对电价加以约束，配电网制定的电价应不低于储能的单位充放电成本，以此确保微电网的收益；制定的电价也不应过大，否则，微电网为了保证自身收益，会拒绝与配电网产生电能交互。即：

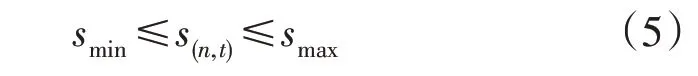
式中：smin为配电网电价的最小值；smax为配电网电价的最大值。

2.2 微电网模型

微电网选取风光柴储式微电网，即由风光机组、微型燃气轮机、储能和负荷组成。

2.2.1 目标函数

微电网模型为双层模型，分为上层和下层。上层以微电网年化总成本最低为目标函数，确定储能容量，将储能容量下发给下层。微电网年化总成本为：

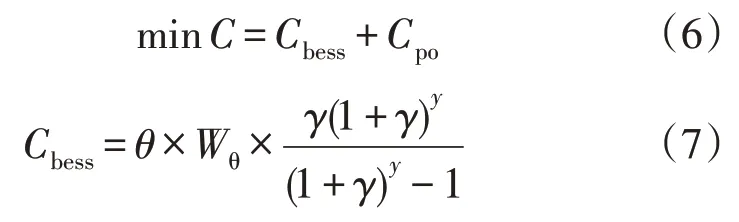
式中：C为微电网年化总成本；Cbess为年化储能容量投资成本；Cpo为微电网的年运行维护费用；θ为储能容量；Wθ为单位容量成本系数；γ为折现率；y为储能寿命。

下层接收到上层确定的容量后，以微电网的年运行维护费用最低为目标函数，对运行策略进行优化，返回上层，形成双层模型。微电网的年运行维护费用为：

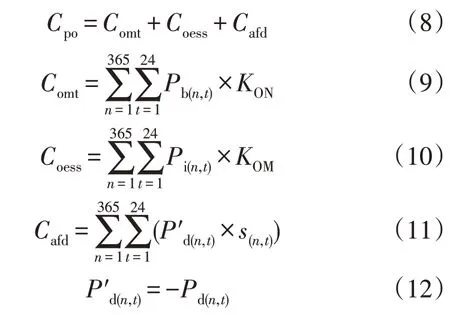
式中：Comt为微型燃气轮机的燃料及碳排放费用；Coess为储能的运行维护费用；Cafd为微电网与配电网的购售电费用；Pb(n,t)为第n天各时刻微燃机的出力；KON为单位燃料及碳排放成本系数；Pi(n,t)为第n天各时刻储能的充放电功率；KOM为单位充放电成本系数；P′d(n,t)为第n天各时刻微电网的购售电功率。

2.2.2 约束条件

微电网模型中主要考虑微电网内部的功率平衡约束、储能和微型燃气轮机的运行约束、与配电网的联络线功率约束。

1）功率平衡约束：

式中：PWT,t，PPV,t，Pi,t，Pb,t，P′d,t，Pload,t分别为微电网1 d 内各时刻风力发电功率、光伏发电功率、储能的充放电功率、微型燃气轮机的出力功率、微电网与配电网的联络线功率、微电网内的负荷功率。

2）储能荷电状态约束：

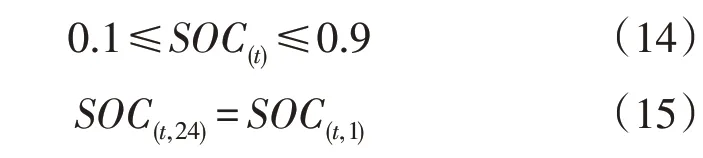
式中：SOC(t)为1 d 内各时刻微电网储能的荷电状态；SOC(t,24)为24：00 时微电网储能的荷电状态；SOC(t,1)为1：00 时微电网储能的荷电状态，SOC(t,1)的取值为0.1。

3）储能充放电功率约束：

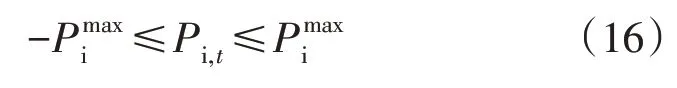
4）微型燃气轮机约束：

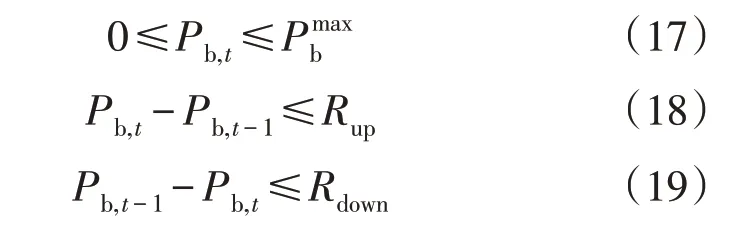
5）联络线功率约束：

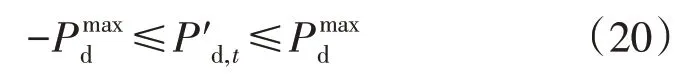
3 模型求解

多微电网主从博弈模型为由配电网模型与多微电网双层模型构成的三层模型。主体配电网模型的优化核心在于求取配电网针对多微电网的最优报价策略。而从体的规划目标在于根据下发报价得出适合该微电网的最优储能容量配置与各时段的购售电功率。基于此，本文采用粒子群算法-退火算法-麻雀搜索算法[24]进行求解。

3.1 配电网模型迭代求解

配电网模型的目标函数受到多微电网的容量及运行策略的影响，因此采用粒子群算法，嵌套微电网双层模型进行迭代求解。配电网模型求解流程图如图2 所示。

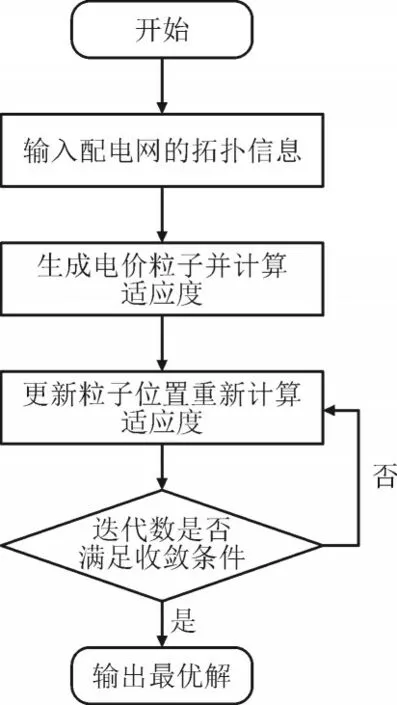
图2 配电网模型求解流程图Fig.2 Solving process of distribution network model

配电网模型求解步骤如下：

1）输入配电网拓扑信息。

2）根据配电网模型约束生成电价粒子。

3）结合微电网双层模型计算各粒子适应度，即配电网年运行成本，得到全局最优解。

4）更新粒子位置。

5）计算更新后粒子适应度，更新全局最优粒子与历代最优粒子。

6）判断迭代数是否满足收敛条件，若满足则输出最优解，否则返回步骤4）。

3.2 微电网模型迭代求解

微电网模型在求解时，电价由配电网下发得到，为已知值，风光出力及负荷采用典型日的数据。双层模型中上层下发容量至下层，容量变化引起运行策略变化；下层将运行策略返回至上层，对容量进行修正。上层采用退火算法，而下层约束条件较多，采用求解速度和精度较高的麻雀搜索算法求解，最终得出各个微电网在该价格下的最优容量和对应最优运行策略。微电网模型求解流程图如图3 所示。

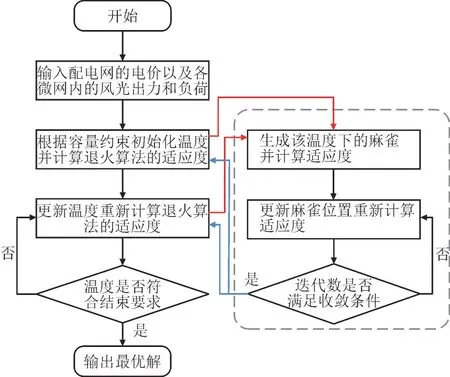
图3 微电网模型求解流程图Fig.3 Solving process of microgrid model

微电网双层模型求解步骤如下：

1）输入配电网下发的各时段电价典型日初始电价、各微网内风光出力和负荷。

2）根据容量约束初始化退火算法的温度。

3）根据微电网模型的约束条件，产生该温度下包含运行策略信息的麻雀。

4）计算各麻雀适应度，即各微电网年运行成本，并将麻雀群分为觅食者、跟随者和警戒者。

5）更新3 类麻雀位置。

6）计算更新后麻雀适应度。

7）判断迭代数是否满足收敛条件，若满足则得到最优运行策略，否则返回步骤4）。

8）根据所得运行策略计算该温度下的目标函数。

9）判断温度是否符合结束要求，若符合则输出最优解，否则降温并返回步骤2）。

4 算例分析

4.1 场景描述

本文在原有的IEEE33 节点系统中接入3 个微电网，分别接在21 节点、24 节点、32 节点处，均通过联络线与配电网相连，系统结构如图4 所示，网络参数见文献[25]。各微电网的典型日风光出力及负荷曲线如图5 所示，模型参数设置如表1 所示。

表1 模型参数设置Table 1 Setting of model parameters

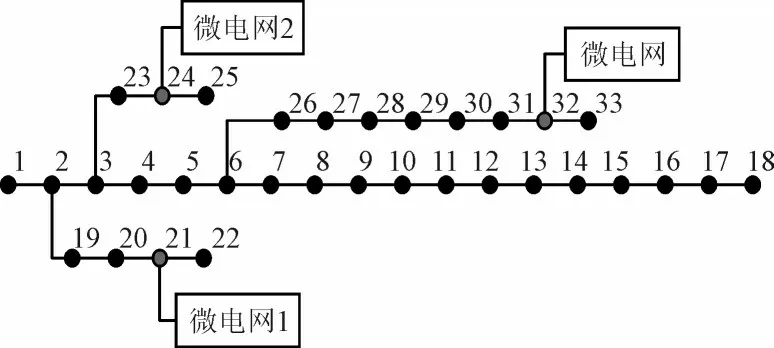
图4 系统结构图Fig.4 System structure

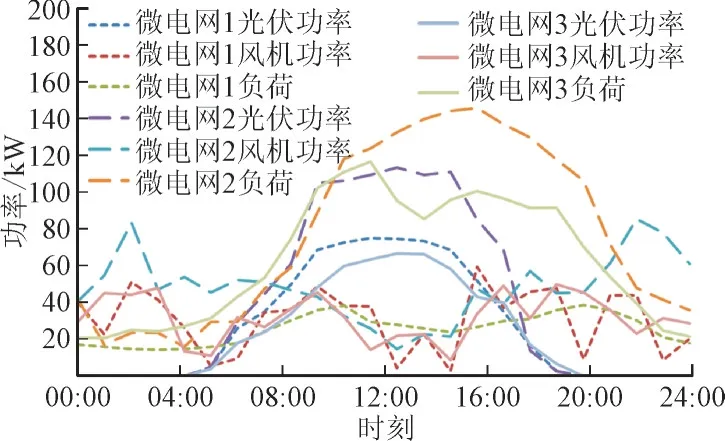
图5 各微电网典型日风光出力及负荷Fig.5 Typical daily wind and photovoltaic power output and load of each microgrid

4.2 配电网的效益分析

主从博弈模型中初始电价采用一般工商业峰谷电价，高峰时段为每日15：00—17：00 和20：00—22：00，低谷时段为1：00—8：00，其余时段为平时段。模型最终收敛后，其电价即为最优电价，优化前后电价对比如表2 所示。

表2 优化前后电价Table 2 Electricity price before and after optimization[元·（kWh）-1]

优化后的电价方案下调了峰时电价和谷时电价，上调了平时电价，使微电网和配电网的收益均得到提升。配电网的运行成本由购售电成本和网损成本组成，因此其取决于微电网的购售电策略和配电网的网损电量。优化前后各微电网的购售电策略及配电网网损电量如图6、图7 所示。图6 中正值为微电网向配电网购电，负值为微电网向配电网售电。

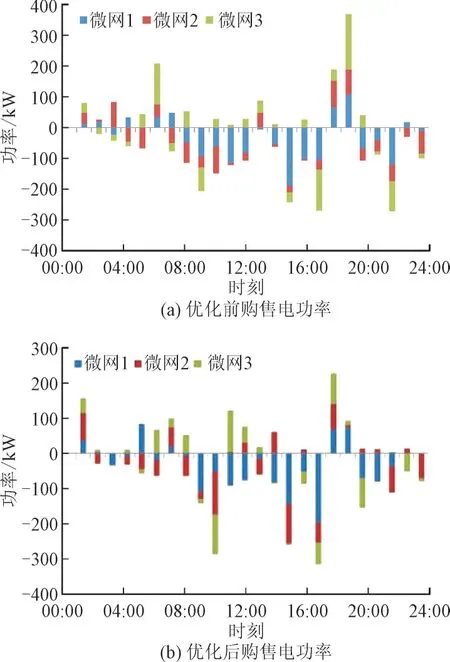
图6 优化前后各微电网的购售电功率Fig.6 Power purchasing and selling of each microgrid before and after optimization

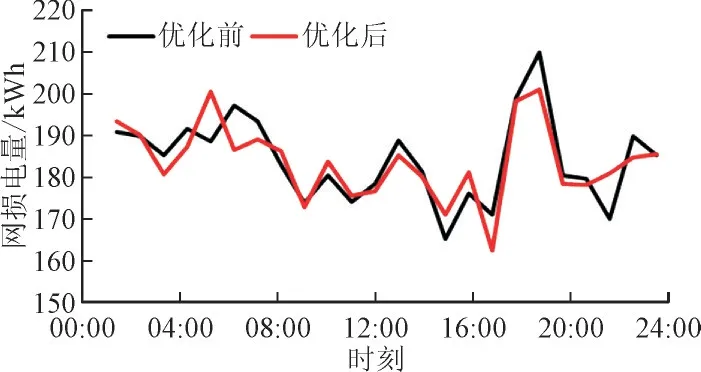
图7 优化前后配电网的网损电量Fig.7 Network loss of distribution network before and after optimization

从图6 可以看出，19:00 时初始电价下的各微网购售电功率达到峰值，3 个微网此时的购电功率均较大，使得配电网的网损电量偏高。在图7 中19:00 时初始电价下的配电网网损电量达到峰值。而电价优化后，配电网通过价格杠杆，适当调高19:00时的电价，即平时电价，使得19:00 时的各微网购电功率大幅下降，从而降低配电网网损，使配电网的网损电量峰值明显降低。

22:00 时属于峰值电价时段，优化后的峰值电价降低，导致各个微电网内的售电功率均降低，但此时配电网的网损电量反而升高。这是由于配电网调低峰值电价，降低各个微网的售电功率，使得此时配电网的交易成本减少，优化后22:00 时配电网减少的交易成本大于增加的网损成本，最终使配电网的年运行成本降低。

表3 给出了电价优化前后配电网的运行成本对比。从表3 可以看出，配电网通过对电价进行调整，从而调控各个微电网的购售电功率，使微电网并网后的网损电量显著降低，从而大幅度降低网损成本。而微电网作为博弈从体，同样追求自身利益最大化，配电网的交易成本增加，微电网通过电能交易获取了更高的收益。配电网的网损成本降低，交易成本升高，一增一减，最终配电网的年运行成本也明显降低，体现了通过价格杠杆对微电网储能容量进行优化配置后，提升了微电网储能充放电的协调性。

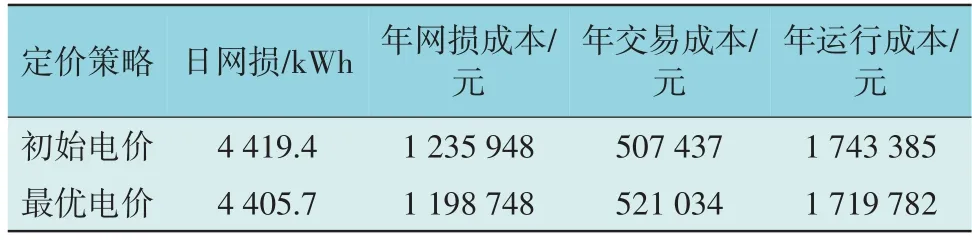
表3 优化前后配电网运行成本Table 3 Operation cost of distribution network before and after optimization

4.3 微电网的效益分析

表4 为优化前后各微电网储能容量对比，表5为优化前后各微电网的年收益对比。

表4 优化前后各微电网储能容量Table 4 Energy storage capacity of each microgrid before and after optimization kWh

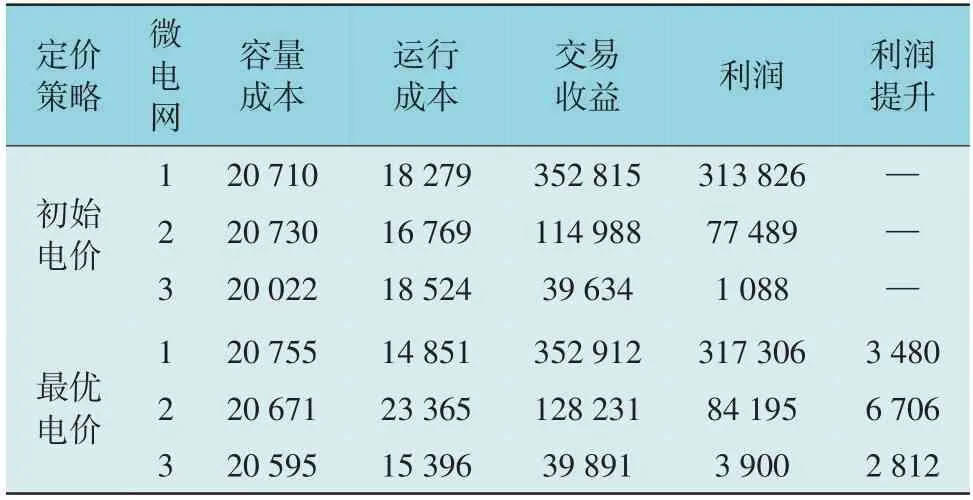
表5 优化前后各微电网的年收益Table 5 Annual revenue of each microgrid before and after optimization 元

由表4 和表5 可以看出，在容量上，微电网1和微电网2 的容量变化较小，而微电网3 的容量则有明显变化，增加了9.31 kWh。虽然容量增大导致相应的容量成本增加，但是微电网3 的运行成本降低，交易收益增加，最终利润提升。在运行成本上，微电网1 和微电网3 的运行成本降低，说明通过配电网对电价的调整，微电网1 和微电网3 减小了储能的充放电功率，运行成本随之降低。微电网2 优化后的运行成本反而升高，说明储能的充放电功率增加，但是更高的运行成本使微电网2 的交易收益显著增加，最优电价下的交易收益较初始电价下提高了11.5%。两相抵消之下，微电网2 的利润也有明显提升。

以微电网3 为例，图8 为微电网3 优化前后的储能充放电功率和购售电功率。红色为微电网购售电功率，正为购电，负为售电。蓝色为储能充放电功率，正为放电，负为充电。由图8 可以看出，初始电价下储能充放电功率和购售电功率的峰值在19:00 时，属于平时段，在图7 中19:00 时配电网的网损电量也达到峰值。因此，配电网调高平时段电价，降低了微电网3 在19:00 时的购电功率，从而使19:00 时的网损电量有明显降低，比初始电价时减少了9 kWh。此外，17:00 时，初始电价下微电网3的储能充放电功率和购售电功率也较高，17:00 时属于峰时段，微电网为了获取高额收益，尽可能多地向配电网售电。配电网调低峰时段电价，降低微电网3 的售电积极性，使微电网3 少售电，降低了17:00 处配电网的网损电量。电价优化后储能充放电功率和购售电功率在10:00 和11:00 时较高，相比初始电价下有明显提升，这是因为微电网3 在博弈过程中需要保证自身的收益。这两个时刻的充放电功率和购售电功率升高，使得配电网的网损电量略微增大，但是增大幅度不明显，总共仅增大了4.7 kWh，远远低于19:00 时配电网降低的网损电量。

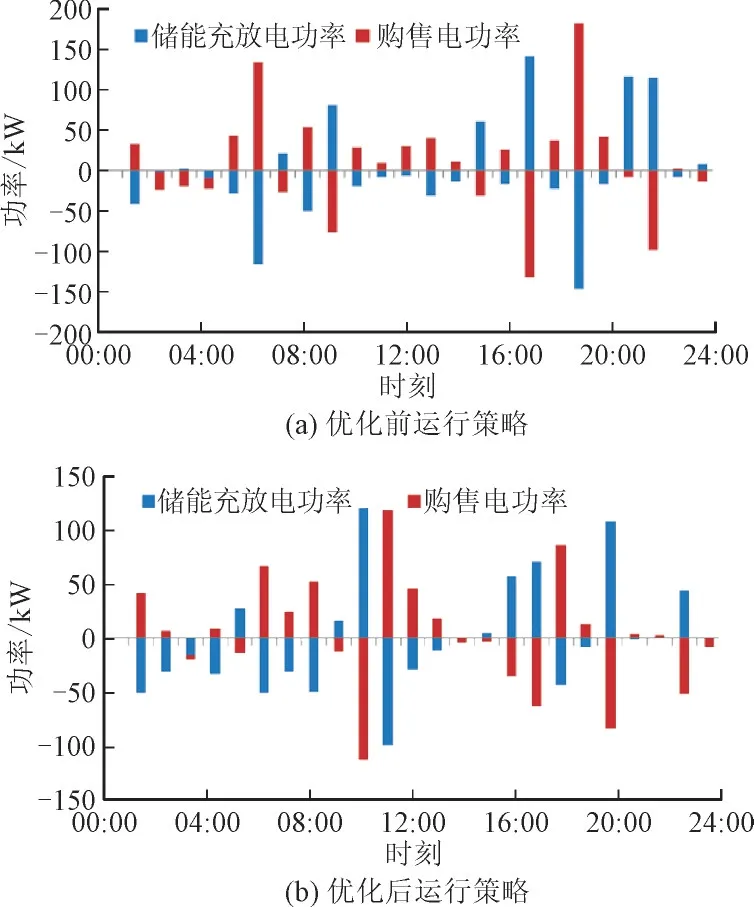
图8 优化前后微电网3的运行策略Fig.8 Operation strategy for microgrid 3 before and after optimization

因此，配电网通过调整电价，从而调控微电网储能的容量和充放电功率，在保证微电网自身收益的基础上，对配电网的运行提供支撑，提升了微电网储能充放电的协调性。

5 结论

本文为了充分发挥价格杠杆在多微电网储能配置中的作用，提升微电网储能充放电协调性，提出了一种基于主从博弈的多微电网储能容量优化配置方法，在多微电网储能建设阶段兼顾微电网和配电网的经济性，以电价为杠杆，对微电网的储能容量进行优化配置。算例分析表明本文提出的优化配置方案有以下特点：

1）在微电网储能容量的配置过程中考虑运行策略对容量规划的影响，以微电网自身经济性为目标，建立储能容量双层优化模型配置，合理调控储能容量和运行策略。

2）引入价格杠杆，同时考虑配电网和多微电网的利益，在保证各微电网收益的前提下，降低了配电网的网损电量，从而减少配电网的运行成本，提升了储能充放电的协调性。

本文暂未考虑风光随机性对微电网储能容量配置的影响，且仅在峰谷制电价模式下验证了所提方法的有效性。后续研究工作中将考虑采用实时电价模式，并对风光随机性进行处理，探索更加完善有效的优化配置方法，以促进微电网和配电网的协调持续发展。