带运算放大器的热敏电阻电桥电路分析与设计
无锡南洋职业技术学院智能装备与信息工程学院 代淑芬
热敏电阻是一种新型的半导体测温元件[1]。热敏电阻应用于温度检测灵敏度高且具有结构简单、电阻率小、适用于动态测量等突出优点,但由于热敏电阻存在其固有的热电非线性,严重影响着温度测量范围的扩大和温度测量精度[2]。NTC 热敏电阻的非线性非常严重,因此在实际应用中对NTC 热敏电阻的非线性处理就非常关键。本设计应用数学建模的方法,通过对接口电路参数的分析计算,推导出最佳的线性化补偿方法。
1 最佳线性化
用模拟电路实现最佳线性化对NTC 热敏电阻的非线性进行线性补偿。首先要选择并实现最佳拟合直线。
如图1 所示为分压式接口电路,首先通过数学建模的方法列出其电路方程,如式(1)所示:
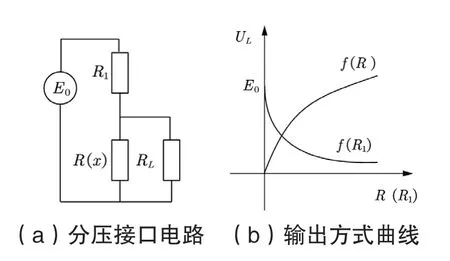
图1 参数式敏感元件分压接口Fig.1 Voltage divider interface of parametric sensitive element

将电路方程进行归一化处理,如式(2)所示:

式中:x是输入信号,。根据输入温度范围条件,选择一平衡点x=x0。为了获得最大线性范围输出,将平衡点选在输入范围的中点。为了电路在平衡点x0附近的小范围内具有最佳线性化输出恃性,将公式(2)在平衡点附近展开成泰勒级数,如式(3)所示:

在式(3)中,若令二次项系数为零k''(x0)=0,并且忽略三阶以上非线性,则可得线性方程如式(4)所示:
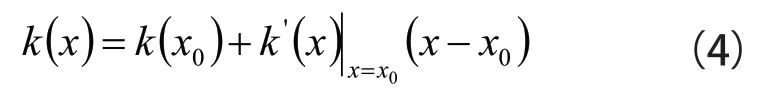
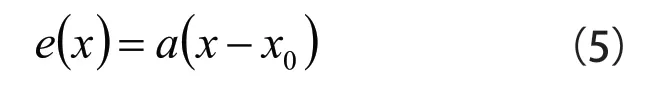
通过公式(5)可知,e(x)与x间具有线性关系,其线性化条件为:
(1)x必须在平衡点x0附近小范围内变化;
(2)k(x)在平衡点x0上具有各阶导数。
在满足上述条件下,线性化的条件是平衡点x0上的二阶导数为零,同时忽略三阶以上导数。
利用泰勒级数,并令二次项系数为零,选择过平衡点的切线(其斜率为常数)的直线作拟合直线,即常数

由此可得线性化条件,如式(6)、式(7)所示:

式(7)表达了定值电阻R1与感温电阻R(x)在平衡点x0上的导数值的关系。一般R(x)为正值;但当R''(x0)为负值时,则定值电阻R1必为负值。这表明,当R(x)的二阶导数为负值时,不能用纯电阻网络实现定值电阻R1的设计,而只能用有源网络实现阻值为负值的R1。本设计中,热敏电阻的二阶导数为正值,如图2 所示,所以热敏电阻电路的线性化可用电阻网络实现。

图2 测温电阻特性Fig.2 Temperature resistance characteristics
2 热敏电阻接口电路分析与设计
传感器接口电路是传感器与检测控制系统之间相连接的中间环节,其性能直接影响到整个系统的测量精度和灵敏度[3]。热敏电阻一般为过渡金属铁族混合氧化物的制备物,实用温度范围-200℃~200℃。热敏电阻接口电路必须外加激励电源。但热敏电阻通电后会产生自加热效应,因而引起温升,影响感温精度。因此,热敏电阻激励电源的电压或电流应有所限制。
热敏电阻具有较高的温度灵敏度,同时也具有很高的非线性,可用指数函数表达热敏电阻方程,如式(8)所示:
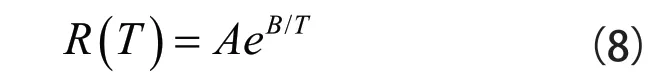
式(8)中T 为绝对温度,A 和B 称热敏电阻常数,与元件及其制备材料的特性有关,可以通过在两个标准温度下的实测确定。
将式(8)代入式(7),可求得串接变换方式最佳线性化条件下的R1取值,如式(9)所示:

式(9)中T0是选择的平衡点温度。设输入温度范围0℃~50℃,平衡温度25℃(T0=298K),热敏电阻常数A=0.0585Ω,B=3260K。取E0=5V,可由式(9)算得R1=2278Ω。由式(4)、式(1)算得最大相对非线性误差约为4%。
3 带运算放大器的热敏电阻电桥电路分析与设计
带运放的热敏电阻电桥电路如图 3 所示。
这种电路的最大优点是输出电压对地可为零,是分压电路、纯电阻电桥电路所不具备的特点。根据图3 电路,并利用理想运放条件,可推导出电路方程如式(10)所示:

图3 带运放电桥电路Fig.3 Bridge circuit with op amp
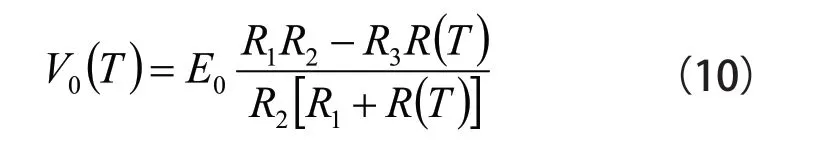
根据热敏电阻公式(8),若设平衡温度为T0,可将热敏电阻方程作如式(11)、式(12)所示的变换:

设平衡温度为T0,即x=1,将归一化电路方程在平衡点x=1 展开成泰勒级数,如式(15)所示:
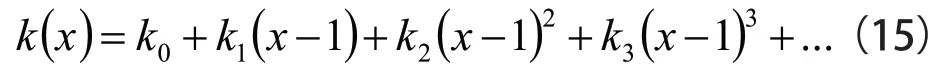
式中展开系数如式(16)-式(19)所示:
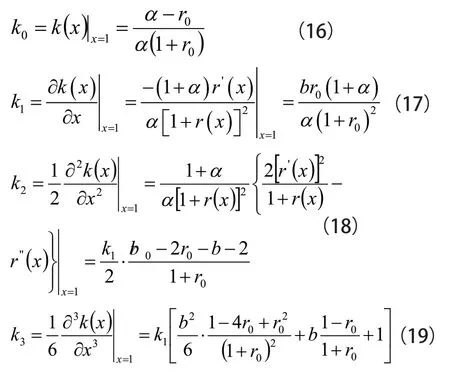
根据最佳线性化条件k2=0可得到如式(20)、式(21)所示:


将式(17)代入式(18),得到如式(22)所示:
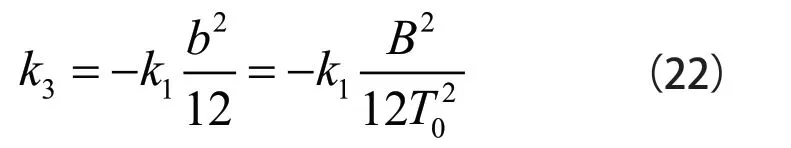
若设计在平衡点时的输出为零,则k0=0,可得如式(23)所示:
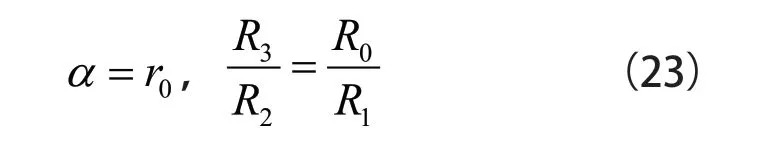
在k0=0、k2=0,平衡点零输出线性化条件下有如式(24)所示:
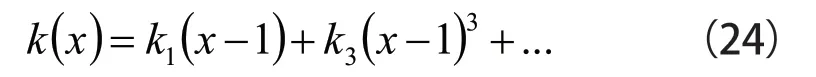
若仅考虑立方项引起的立方非线性误差,则相对立方非线性误差如式(25)所示:

设输入温度范围-25℃~35℃(T=248K~308K),在5℃(T=278K)时输出电压为零,在35℃时的最大输出电压约为1V,最大相对非线性误差为D=0.1,计算图3电路在最佳线性化条件下的电路参数值。
选平衡温度为5℃(T0=278K),则归一化参数x的上限和下限值如式(26)、式(27)所示:

根据最大非线性误差的要求,可列如式(28)所示:
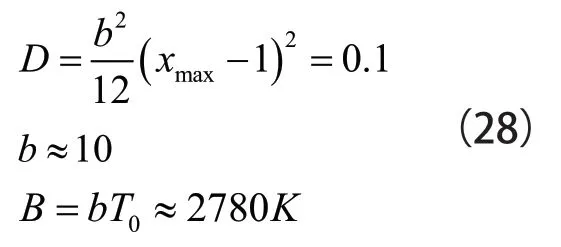
可见,根据最大非线性误差的要求,应选用热敏电阻常数B≈2780K的元件。由式(23)可得到如式(29)所示:

若热敏电阻的另一个常数A=0.4441Ω,则得到如式(30)所示:

若取R3=10Ω,则由,可得R2=1.5KΩ。根据35℃时最大输出电压约为1V 的需求,可得到如式(31)所示:
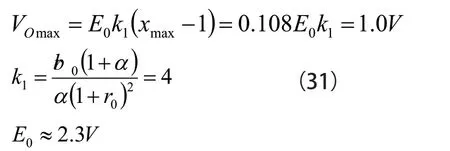
将上面计算的参数代入电路方程可得如式(32)所示:

由此可计算偏离拟合直线的误差并画输出曲线和误差曲线如图4 所示。

图4 带运放电桥输出特性与误差Fig.4 Output characteristic and error of bridge with op amp
4 结语
上述关于NTC 热敏电阻非线性的线性化处理方法,是令电路方程在平衡点的泰勒级数的二次项系数为零,对电路元件参数进行最佳线性化分析和设计,具体总结如下:(1)根据工程实际需要,选择一种热敏电阻接口变换电路方式,并列出电路方程。要拟定或选择一热敏电阻接口变换电路方式,显然需要具备一定数置的热敏电阻接口变换电路的知识积累或实践经验。知识的积累必须通过一定数量的电路分析和实践才能获得;(2)选择一个平衡点,并对电路方程利用泰勒级数进行展开。为了获得较大线性范围的输出,平衡点的选择,对应输入温度范围的中点和输出范围的中点;(3)选择过平衡点的切线为拟合直线。具体做法如下:令泰勒级数的二次项系数为零,则一次项系数必为常数。
引用
[1] 梁森.自动检测与转换技术(第4版)[M].北京:机械工业出版社,2021.
[2] 于丽丽,王剑华,殳伟群.NTC热敏电阻器在高精度温度测量中的应用[J].传感器技术,2004,23(12):75-77.
[3] 王时,晁雯,高菲,等.传感器接口电路中电桥电路的应用[J].电子制作,2016(2):85-86.

