基于塔克分解的浓度重建方法
王才谦 刘石
1.华北电力大学能源动力与机械工程学院;2.华北电力大学控制与计算机工程学院
针对流场中存在复杂机械结构而导致得浓度难以测量的问题,提出了基于塔克分解的浓度重建算法。采用塔克分解对样本数据库进行特征提取,将其运用于浓度分布重建。为了验证算法的可行性,进行了泄漏仿真实验。仿真实验结果表明浓度重建算法可以快速重建浓度分布。最后将本方法与基于主成分分析的重建方法进行比较,实验数据表明本方法在三维浓度重建上具有更好的重建精度。
流场中的浓度信息可以通过实验测量和数值计算获得。其中实验测量主要可分为接触式与非接触式两大类。接触式测量通过将传感器放置在流场中进行采样测量,只能获取流场少数位置的浓度值,无法获取全场的瞬时浓度。若要进行多点同时采样,需要大量的采样仪器与分析设备,测量成本高。非接触式测量利用流体的光学[1]或者声学[2]特性进行浓度测量,但是这些设备也会有结构复杂、布置困难、易受环境影响等问题,一定程度上制约了非接触时测量的应用。近年来,随着计算流体力学的发展与计算机水平的进步,数值计算广泛地运用于流场分析中。但是要想求解流场的浓度值信息,需要获取流场的边界条件,因此在边界条件未知时,就难以使用数值计算方法。而且使用数值计算方法需要大量的计算资源和时间,很难实时获取流场的浓度值信息。
本文的主要工作是将数值计算方法和测量方法结合起来,提出一种基于塔克分解的浓度重建算法。该算法将CFD 数值模拟得到的流场浓度值作为先验信息,然后将先验信息降维提取主要特征后,结合测量的少量浓度值,重建出全场的浓度分布。
1 算法原理
基于特征提取的数据处理方法最早运用于屋盖风压场的重建[3],后来又广泛运用于其他流场参数的重建过程中:QIN 等人[4]将主成分分析、CFD 计算数据结合起来,实现了对风场分布的快速预测;Sun 等人[5]提出一种基于本征正交分解的风速重建方法,并且对测量点位置进行了优化,减少了重建误差;陈敏鑫等人[6]将主成分分析引入到温度分布重建工作中,利用经验数据和少量测量数据快速准确地完成了温度分布重建。但是以上方法研究的均是二维平面上流场参数的重建,所使用的均是基于向量或矩阵的数据降维方法。如果将这些方法运用于三维流场的重建,会在一定程度上造成三维空间特征的损失,为了避免这一情况出现,本文引入了塔克分解作为降维算法对先验信息进行特征提取。
1.1 塔克分解
随着对数据的深入研究,矩阵已经很难完整表述出数据的时空关系。而张量作为可以表征高阶数据的多维数组,可以完整地保留各维度的信息。张量的构成如图1所示。
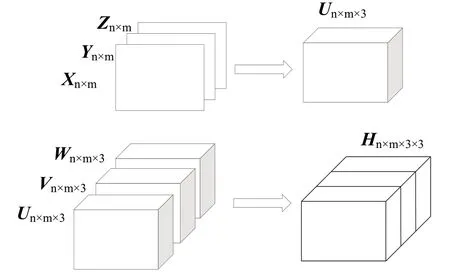
图1 张量示意图Fig.1 Tensor diagram
1963 年Tucker 首次提出了塔克分解,将一个n 阶高维的张量,得到n 个分解因子矩阵和一个n 阶低维的核心张量。n 阶高维张量的分解过程的公式如式(1)所示:


图2 三阶张量塔克分解示意图Fig.2 Schematic diagram of the third-order tensor Tucker decomposition
1.2 浓度分布重建算法
利用经验数据或者测量数据获得n 个工况下的三维浓度分布,组成一份先验数据集XT={X1,X2,…,。对先验数据集XT 进行塔克分解将其分解成核心张量与分解因子矩阵模态积的形式,如式(2)所示。

将XT 与F(4)内的元素展开,公式(2)可转化为如式(3)所示形式:

式中,bi为4 模态方向上的分解因子矩阵中的第i 个因子向量,
由公式(3)可得:

那么对于待重建的三维浓度分布XR,如式(5)所示:

式中,b 为4 模态方向上待重建的三维浓度分布XR所对应的分解因子向量。
根据模态积的定义将式(5)从张量形式转化为矩阵与向量相乘的形式,如式(6)所示:
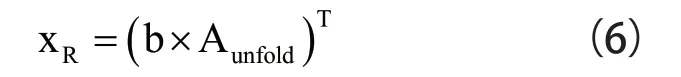
式中,xR为将三维浓度分布XR中的元素转换为向量形式,维度为(n1×n2×n3)×1;Aunfold为将重建系数张量沿着模态4 方向展开的矩阵形式,维度为(n1×n2×n3)×m4。
少量的测量数据与整个流场的浓度分布的位置关系可由式(7)表示。

式中,y 为实际测量得到的数据,维数为r×1,其中r为测点数目;M 为浓度测量矩阵,维数为r×(n1×n2×n3)。浓度测量矩阵M 为0-1 矩阵,每一行只有一个元素的值为1,其余元素的值为0。在第n 行(n 取1 到r),值为1 的元素所在的位置,代表了第n 个测量点与全部浓度点的相对位置。
为了使重建的三维浓度分布与实际的三维浓度分布相等,即x=xR,把式(6)代入到式(7)中,可以得到如式(8)所示:

在式(8)中,y 通过测量获得,M 为测量矩阵,在决定好测点位置后为已知量,通过对样本数据张量XT 进行塔克分解后获得,因此可以先用最小二乘法求解出式(8)中的b,再代入式(6)即可求解出待重建的三维浓度分布。
最后为了检验重建效果,定义相对重建误差:

基于塔克分解的浓度重建算法如图3 所示。从图3中可以看出,完成重建算法的第一步是利用CFD 进行数值模拟,得到边界条件下浓度场分布数据集;第二步是对样本张量进行塔克分解,求解其核心张量与各个模态方向上的分解因子矩阵;第三步是求解重建系数张量,并将其展开为重建系数矩阵;第四步是得到各测点的位置与测量的浓度值;最后计算待重建的浓度分布向量所对应的分解因子向量b,进而求出重建结果。

图3 基于塔克分解的浓度重建算法流程图Fig.3 Flow chart of concentration reconstruction algorithm based on tak decomposition
2 案例验证
为了验证算法的可靠性,建立泄漏模型。使用前处理软件ICEM 建立几何结构并划分网格,使用Fluent17.0进行仿真求解。
2.1 模型几何信息
泄漏模型如图4所示,整个容器的计算尺寸为200mm×200mm×875mm,水流入口取水在容器中经过稳流装置后的截面,金属棒下端固定在距水流入口50mm 高的位置上,每个金属棒长565mm,为了简化计算,固定装置忽略不计,水流出口的截面尺寸为60mm×40mm。冷却水从下方的水流入口进入,经过金属棒然后从水流出口流出。中间的金属棒在高度为420mm 的位置上存在一个直径为3mm 的圆形破口,方向朝着x 轴正方向。泄漏物会由于浓度差以及流体携带等机制向水中扩散和传输,最终随水流从出口排出。
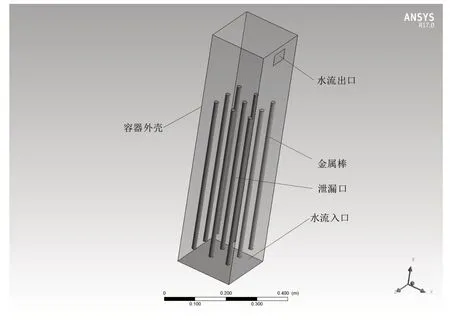
图4 流动模型结构图Fig.4 Flow model structure diagram
从图4 中可以看出,9 根金属棒遮挡了整个容器下半部分的浓度分布,很难直接测量这些区域的浓度值,而金属棒上方的浓度分布是可以利用前文中提到的测量方式测量的。因此泄漏模型验证的目的是利用金属棒上方区域可测量的浓度分布来重建出金属棒遮挡区域不可测量的浓度分布。
2.2 网格划分
结构化网格具有生成速度快、网格质量高、数据结构简单等优点,但是对于不规则区域的适应性较差。由于前文中对本模型进行了简化,几何结构并不复杂,因此使用结构化网格进行网格划分。
一般来说网格数量越多,计算结果就能更加精确,但是计算耗时也会变长。为了在从稀疏到密集的5 组网格中选取一个合适的网格节点数,在保证精度的前提下减少计算耗时,对这5 组网格进行网格无关性检验。5组网格的网格数分别为1131852、1729692、2658972、4526216、6142286。选取中间金属棒顶端中心到水流出口中心所连成的线段上100 个点的流速作为检验计算结果的判断标准,不同网格数目下样本点流速如图5 所示。
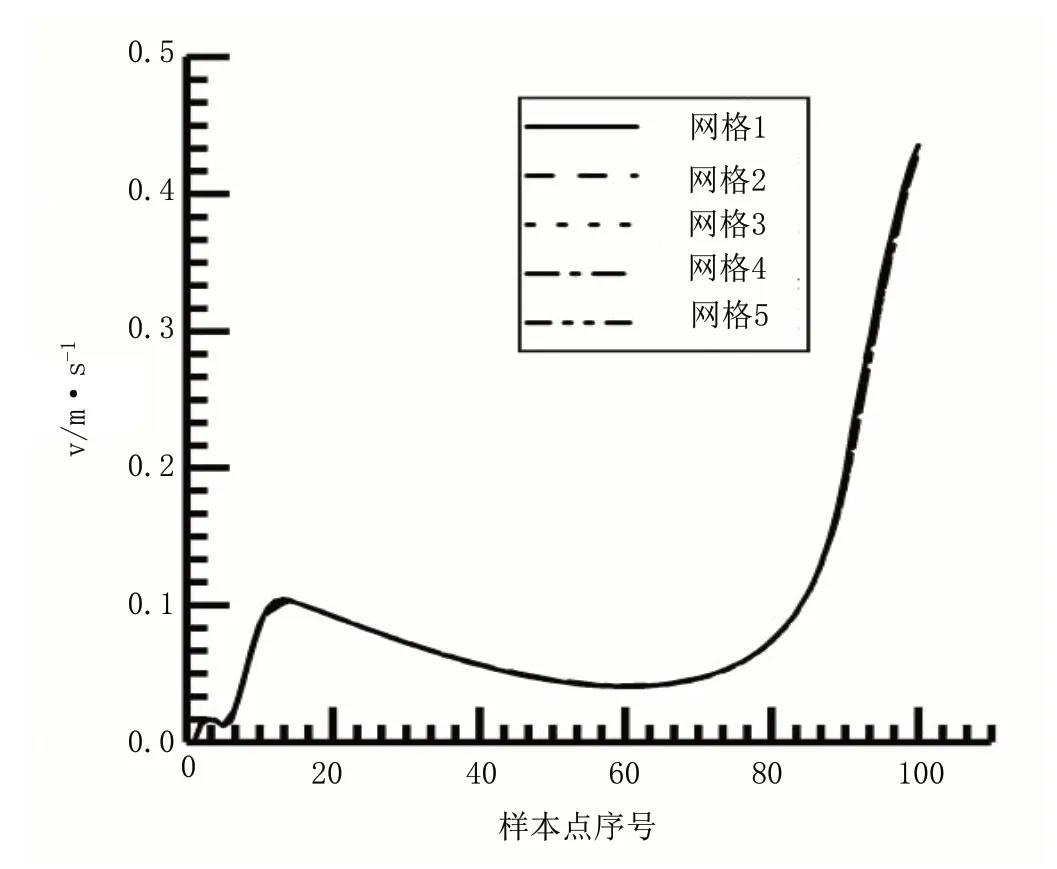
图5 不同网格数下各样本点流速Fig.5 Flow velocity of each sample point under different grid numbers
观察样本点折线可得,使用以上网格所计算出的结果差别不大,考虑到在网格数为1131852 时计算速度最快,因此在本文中仿真使用网格数为1131852 的网格。
2.3 计算模型
泄漏实验的泄漏物为罗丹明B 水溶液,由于溶液的浓度不高,且不会与水发生化学反应,其物理性质仍按照水的性质设置。泄漏物与水都视为不可压缩流体,对于水流的湍流流动,采用k-ε 湍流模型方程并结合连续性方程和动量守恒方程进行三维仿真。选择速度、压力的耦合求解算法,动量和湍动能采用二阶迎风格式求解。水流入口和泄漏口设定为速度入口,水流出口设定为压力出口,出口压力设为0pa。残差的收敛条件设为10e-4,根据残差和出口、入口质量守恒来判断计算是否收敛。
3 重建结果
本文将重建区域的三维空间用几个堆叠的平面来表示。由于计算结果中越靠近z=0m 处的浓度值较高,越靠近z=±0.1m 处的浓度值较低,而浓度值较低的点对浓度重建的意义不大,因此本文中选取z=-0.04m,z=-0.02m,z=0m,z=0.02m,z=0.04m 五个平面来代表整个三维流体域,如图6 阴影部分所示。

图6 堆叠平面示意图Fig.6 Stacked floor plan
每个平面中浓度点的排列方式为:在x 方向上从x=-0.1m 开始到x=0.1m 结束,每隔0.002m 设置一个浓度点,共设置101 个;在y 方向上从y=0.42m 开始到y=0.82m 结束,每隔0.002m 设置一个浓度点,共设置201个,每一个平面的浓度点数目为20301 个。本文根据不同的水流速与泄漏物流速设置36 个边界条件作为样本工况,水流速分别为0.01、0.02、0.03、0.04、0.05 和0.06m/s,泄漏物流速分别为0.01、0.02、0.03、0.04、0.05 和0.06m/s。将样本工况计算完成后,建立一个101×201×5×36 的四维张量样本数据库。
另外,在实际测量的过程中,只知道测量点的浓度分布,不知道水流速度与泄漏物泄漏速度这些边界条件,测量的工况基本上都是在样本工况之外。因此,想要验证浓度重建算法的实用性,还要验证待重建的浓度分布工况位于样本工况外的重建结果,因此除了36 个样本工况外还设置了5 个测试工况,构成了一个维数为101×201×5×5 的四维张量测试数据集。
从高度在0.62m 以上的浓度点(即没有被金属棒遮挡的区域的浓度点)中随机选取400 个点作为测量点数据带入到重建算法中,三维浓度重建所使用的测试工况如表1 所示。
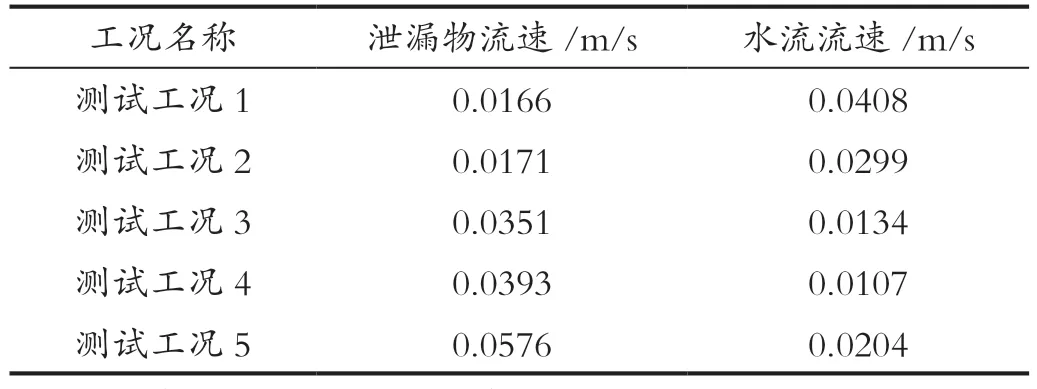
表1 测试工况参数Tab.1 Test condition parameters
经过浓度重建后,5 个测试工况的重建误差如表2所示。

表2 测试工况重建误差Tab.2 Reconstruction error of test conditions
从表2 可得,各测试工况的重建误差均在10%以下,重建时间在1s内,因此只要能够及时获取测量点的浓度值,就可以获得全场的瞬时浓度。重建所得测试工况5的浓度分布如图7 所示,由于各平面的浓度值的数量级差距较大,故将各平面的浓度分布分开展示。
由图7 可以看出,在测试工况不在样本工况范围内的情况下,使用基于塔克分解的浓度重建分布算法在z=±0.02m 和z=0m 这三个平面有较好的重建结果。对于z=±0.04m 两个平面来说,虽然在浓度分布图上的数值计算和重建的结果差距较大,但是这两个平面的浓度值很低,为10-9的数量级,虽然相对重建误差较大,但是绝对误差仍然在一个较小的水平。因此可以认为本算法可以实现对模型浓度分布的有效重建。

图7 各平面数值计算与重建浓度分布对比Fig.7 Comparison of numerical calculation and reconstructed concentration distribution in each plane
此外,在三维浓度分布重建算法的研究中,可以将一个工况下的三维浓度点进行编号,将其储存在一个向量中,计算多个工况的浓度值就形成一个样本矩阵,再采用基于主成分分析的方法来提取特征向量[7]。为了比较该方法与基于塔克分解方法的优劣,另外采用了基于主成分分析的浓度重建算法与基于塔克分解的重建算法进行对比。
如图8 所示,相较于基于塔克分解的重建算法,使用基于主成分分析的重建算法的重建误差在各测试工况下都要更高。而且使用主成分分析的过程中对先验信息的处理会涉及到协方差矩阵的计算,在先验信息维数较高时,计算机甚至会出现内存不足无法处理的情况。因此使用塔克分解的重建算法相较于使用主成分分析的重建算法在三维浓度重建方面具有更好的效果。
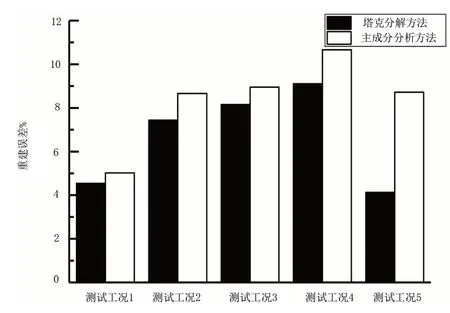
图8 各工况下基于主成分分析与塔克分解的重建算法的重建误差对比Fig.8 Comparison of reconstruction errors of reconstruction algorithms based on principal component analysis and Tucker decomposition under various working conditions
4 结语
本文针对由于技术条件和环境影响难以获取流体域内部浓度信息的问题,将特征提取引入浓度分布重建的研究中,结合了实验测量与数值计算方法,提出了基于塔克分解的三维浓度重建算法,并从原理上论证了算法的可行性,并总结了进行浓度分布重建的计算流程。然后对于泄漏过程进行数值模拟,将数值模拟的结果与重建算法得到的结果进行对比分析,重建结果表明本文的算法能够较准确地重建数值模拟的数据,初步证明了本算法的可行性。最后将本算法与基于主成分分析的浓度重建算法的重建误差进行对比,结果表明了本算法相对于基于主成分分析的浓度重建算法在三维浓度场重建上具有一定的优越性。
本文中的重建误差较大,所使用的测点数目也较多,后期研究将对提升重建精度和降低测量点数目进行进一步探索。
引用
[1] 王雪梅,刘石.基于TDLAS技术的CO_2浓度测量[J].化工自动化及仪表,2016,43(11):1158-1161.
[2] 丁喜波,陈晨,张任,等.基于超声波相位差的气体浓度测量方法[J].高技术通讯,2014,24(2):189-192.
[3] 李元齐,沈祖炎.本征正交分解法在曲面模型风场重构中的应用[J].同济大学学报(自然科学版),2006(1):22-26.
[4] QIN L,LIU S,LONG T,et al.Wind Field Reconstruction Using Dimension-reduction of CFD Data with Experimental Validation[J].Energy,2018,151(May 15):272-288.
[5] SUN S X,LIU S,LIU J,et al.Wind Field Reconstruction Using Inverse Process with Optimal Sensor Placement[J].IEEE Transactions on Sustainable Energy,2018,10(3):1290-1299.
[6] 陈敏鑫,刘石,孙单勋,等.机器学习算法在温度分布重建中的应用[J].自动化仪表,2020,41(1):95-100+105.
[7] 陈敏鑫.基于降维和深度学习方法的温度分布重建[D].北京:华北电力大学(北京),2021.
——以2023年高考湖南卷物理第14题为例

