培养初中生数学问题解决能力的课堂教学实施策略

文/高州市教师发展中心 陈 琼

问题解决是数学教学的中心环节，其目的不是单纯的尽量多和尽量好的解决问题，而应该是以培养问题解决的能力为目的。正如贝格所说：“教授数学的真正理由是因为数学是应用极广的科学，且特别地教授数学还有利于解决各种各样的问题.学习怎样解决问题是学习数学的真正目的。”现在的数学教学不仅是要教学生掌握知识，更重要的是要有由“掌握知识技能为核心”的教学转向“发展思维训练为核心”的教学，形成系统的知识判断能力、高阶思维解决问题能力。

一、把上课的重心转移到预设引领下的生长教学

1.创设切近真实又开放的问题情境

情境化的教学，本质上就是在脱离数学，从实际问题到数学问题的数学抽象的过程，也就是核心素养的抽象能力。开放的情景就是我们利用这个情境素材从不同的维度展开。下面以北师大版数学九年级下册《锐角三角函数》为课例，素材由梯子的倾斜程度问题引入正切的概念，教学时呈现多种形情形；高度相同，底边不同；底边相同，高度不同，等等，让学生讨论，这是一个很好的开放性的问题，学生的回答可能多种多样，比如有的学生可能会想到度量角度，还有的学生可能会想到AC等于ED，因此比较BC和FD的长短，就可判断梯子的倾斜长度。角的改变引起陡的程度的变化，而同样是梯子下滑的素材，但是在2020年的中考题里面，

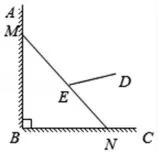
【考题】有一架竖直靠在直角墙面的梯子正在下滑，一只猫紧紧盯住位于梯子正中间的老鼠，等待与老鼠距离最小时扑捉.把墙面、梯子、猫和老鼠都理想化为同一平面内的线或点，模型如图，∠ABC＝90°，点M，N分别在墙面BA，BC上，梯子MN的长度始终保持不变，MN＝6，老鼠E在MN的中点处，猫在D点处，它到墙面BA，BC的距离分别为4和3.在此滑动过程中，猫与老鼠的距离DE的最小值为 .

这个问题观察的重心，跟本节课思考的维度不同，其观察的不是角，而是斜边中线在运动过程中的轨迹问题。

2.预设驱动思考又发散的问题情境

初中数学课堂教学，十多年前在基础知识、基本技能方面落实得比较到位。但缺少了培养学生的数学思维以及四能“发现问题、提出问题、分析问题、解决问题”方面的教学。也就是要用问题引导学生去发现问题、提出问题，同时情境有一定的障碍性，需要一定的逻辑分析能力，要临界于学生的最近发展区，使学生进入“心求通而未得，口欲言而未能”的理想状态.例如：九年级上册《反比例函数的应用》这节课，通过问题设计，引导学生能够运用函数的思维方式去观察、分析现实社会中问题，能用反比例函数解决简单实际问题，

【问题】某蓄水池的排水管每时排水8m3，6h可将满池水全部排空。

（1）蓄水池的容积是____？

（2）如果增加排水管，使每时的排水量达到Q（m3），那么将满池水排空所需的时间t（h）将如何变化？

（3）写出t与Q之间的关系；

（4）如果准备在5h内将满池水排空，那么每时的排水量至少为____？

（5）已知排水管的最大排水量为每时12m3，那么最少____时间可将满池水全部排空？

二、在课堂教学中发展深度学习，培养学生的思维能力

培养学生的思维能力，应该从提高学生的思维品质入手，培养学生思维的深刻性，教育学生学会透过现象看本质，学会全面地思考问题，养成追根究底的习惯。如：我在讲评一道《关于线段、射线、直线概念的理解和运用》的题目“……数轴上表示不小于，且不大于3的点组成的是什么图形？……”孩子们对此不难理解，很快根据定义得出答案：线段！我看到孩子们情绪高涨，抛出一个问题让他们讨论，“数轴上表示大于，且小于3的点组成了什么图形？”。首先题目提出的数轴上的点组成的图形而这图形只能有三种：线段、射线、直线，学生们又从定义和端点个数等多方面展开思考.通过讨论让孩子们加深对相关概念的理解和提高独立思考、分析问题的能力.在教学过程中，一方面要尽量使学生掌握数学概念、原理的本质，提高所掌握的数学知识的抽象程度，因为所掌握的知识越本质、抽象程度越高，其适应的范围就越广泛，思维的灵活性也就越高.在教学中要鼓励学生提出不同的意见，使学生体验到创新思维的乐趣，同时引导学生反思和剖析自身的思维过程，了解自已在学习中运用了哪些基本的思考方法、技能和技巧？它们的合理性如何？效果如何？有没有更好的方法？学习中走过哪些弯路？犯过哪些错误？原因何在？等等.

三、在课堂教学中倡导研究性学习

研究性学习是一种能适应新形势的需要，是培养创新意识和激发创造动机的新兴教学理念。研究性学习进入课堂，是培养学生养成“研究型”认知学习方式的一种有效路径，在研究性学习中以学生为主体，知识的获取途径来自于自身的研究活动，在研究过程中发展学生的分析能力、推理能力、决策能力以及问题解决的能力等。

在课堂上，研究性学习能让学生通过自身的潜能、自主地去获取知识，这种教学模式有助于学生将自已各项技能和各种能力得到最大化的发展，数学问题解决能力得到极大提高。例如，在探索直线平行条件一课中，如何得出“同位角相等，两直线平行”的判定定理时，让学生通过实践“扮演装修工角色”向墙上钉木条，如何使木条a平行木条b，教师从中引导，让学生怎样把实际问题转化为数学问题来，从而得出木条a平行木条b的必要条件是什么？使学生初步感知“同位角”和“同位角相等，两直线平行”的判定定理。接着再引导学生动手操作“借助三角尺画平行线”这一过程，最后学生通过自主探索研究，讨论分析、推理得出结论。

以上是从数学问题解决能力的角度，阐述了在初中数学教学中培养学生问题解决能力的一些基本做法.但问题解决能力是一种综合能力，更需要我们教师在教学中不断探索。