高中数学教师对“高观点数学知识”的理解水平调查

单雪昀（新疆师范大学教育科学学院）

一、问题提出

“会当凌绝顶，一览众山小”对于高观点下的初等数学来说意味着：要站得高、看得远，才能将初等数学问题剖析得简单明了。事实上，自菲利克斯·克莱因提出这一观点后，中国的数学教育也在经历着改革，最直观可见的是高中数学教材新增以大学数学知识为背景的内容，选修教材居多。因此，研究高中数学教师的“高观点数学知识”理解水平现状是有必要的。下面以新疆地区高中数学教师和某大学数学教育方向研究生为测试对象，分成三个数学知识维度（如表1），拟从初等数学问题与大学数学“what”思想或方法有联系的问题入手，探究新疆地区高中数学教师对“高观点数学知识”的理解水平的现状。

表1 数学知识维度具体特征

二、研究设计

1.研究对象

为方便调查师范类准教师与预备教师，针对准高中教师（新疆某大学数学教育方向研究生），以及新疆高中在职数学教师，包括新疆乌鲁木齐市某高中教师、新疆南疆地区暑期国培班高中教师（2018年），采取分层抽样方法，共计发放问卷40份，具体如表2、表3所示。

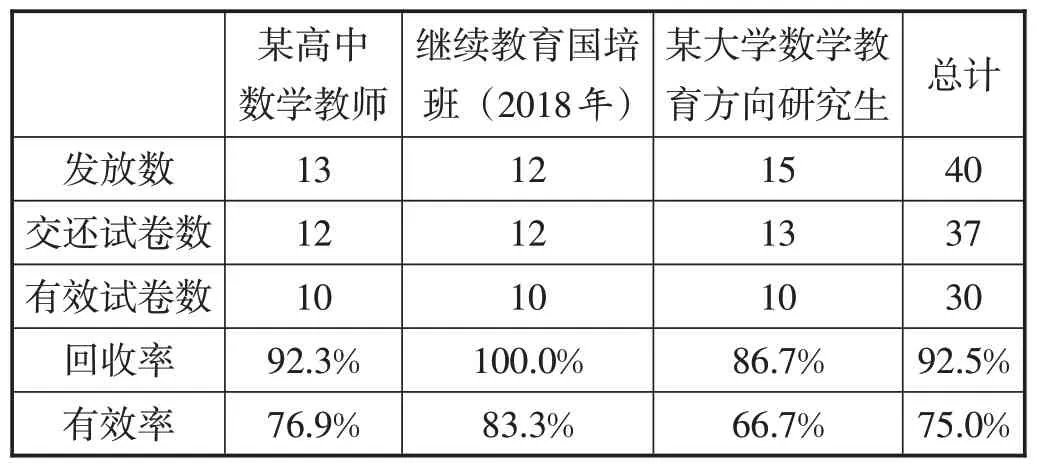
表2 试卷收集情况

表3 被试教师信息分布情况

2.研究工具

（1）评价框架建构。

为建构合理的评价模型，将CIPP教育评价模型作为评价理论基础，以研究问题“高观点数学知识”为核心驱动目标，拟划分三个理解水平维度：操作性、初概念性和探究性，如图1、图2所示。

图1 数学知识结构韦恩图

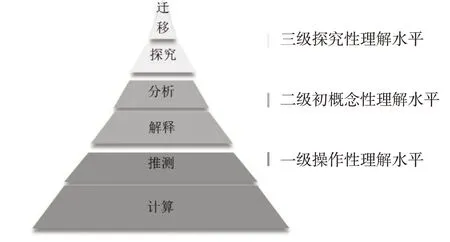
图2 数学理解水平金字塔

这里针对图2中数学理解水平的划分标准进行解释。一级操作性理解水平：教师知道数学的某个事实、概念与方法，但受制于数学教材的初等方法，仅能合情推理，缺乏数学宏观意识。二级初概念性理解水平：教师了解数学概念、性质等，能演绎推理，但易犯循环论证而不自知，无法运用高观点思想窥探初等数学本质。三级探究性理解水平：教师已具备初概念性理解，并能迁移大学数学方法揭示本质解决初等问题，进而纵横地认识数学。

（2）“高观点数学知识”水平测试卷。

测试内容选择与确定考虑最基本问题，以《普通高中数学课程标准（2017年版）》为依据，将内容划分为集合、函数与导数、三角函数与平面向量、数列与不等式、解析几何、立体几何与空间向量、统计与概率、其他部分，又基于彭翕成《从初等数学到高等数学（第1卷）》的观点，将考查视角转到初等数学教材本身，选择函数与导数、数列与不等式、解析几何、立体几何与空间向量、其他部分（二项式定理）5个模块重点考查。采用Microsoft Office Excel数据处理器对被试进行编码录入、汇总，运用SPSS数据软件计算被试关于概念、命题、解题三个方面“高观点数学认知”分别划分探究性、初概念性和操作性层次水平并进行分析。

三、研究结果

1.“高观点”数学概念理解水平

如表4，从数学问题的设计角度看，被测问题属于常规且高频问题，教师理应了解其背后的思想方法。

表4 “高观点”数学理解水平占比表

具体而言，“高观点”数学概念理解水平：探究性理解平均水平较其他数学维度的水平高出10%～18%，大部分教师“高观点”意识高于实际水平。因此，在数学概念方面教师要注重强调对知识的理解与呈现，以看似合理的常识性问题为起点，脱离书本的桎梏，反向思维构建高等数学与初等数学的桥梁，再认识和解决初等问题。“高观点”数学命题理解水平：呈现出被试的探究性和操作性理解水平极不稳定，而初概念及以上理解水平稳定在45%左右的状态，差距大。因此，教师需打破长期教学方式表现的思维恋旧和循环逻辑定式错误，如“导数正（负）则单增（减）的演绎证明”不证自明等现象，逐步培养深度学习，重视并解读学生每一次隐蔽性的数学语言。“高观点”数学解题理解水平：处于初概念及以上水平的教师较之前两个维度要高且稳定，操作性理解水平相对居多。尤其几何和代数这类高考核心问题，教师俯瞰数学问题的广度和深度相对较强，因此“高观点数学知识”理解呈现较高水平。

2.“高观点”数学问题实例分析

问题1：以52为例，解释无理指数幂的含义。

这是人教B版《普通高中课程标准实验教科书·数学1必修》中“基本初等函数（Ⅰ）”第一小节的内容。有4位教师直接类比正整数和分数指数幂的意义，认为“52=，即个5相乘”，曲解数学概念本质，认知水平较低；有16位教师较重视教材涉及的合情推理，从无理数“数”的角度做无限逼近，但欠缺具体、详尽的演绎推理过程；有10位教师是以“数轴”为工具引出夹逼准则，利用不足近似和过剩近似数列逐次逼近，清楚解释52的含义。

问题2：证明指数函数y=2x在(-∞，+∞)上是增函数（试给出每一步充分的推理依据）。

大多数教师在证明过程中极易陷入循环逻辑的怪圈：有21位教师回到单调性的定义，作差（作比），典型的循环论证，出现认知惯性；另有借对数的单调性逆推指数单调性，限定了自变量的取值范围，违反一般性；仅有2位教师运用台阶法，将自变量从整数、有理数、无理数、有理数到无理数逐级证明（高数极限思想），符合大学数学的严谨性分析。

对于解题，如问题“若已知数列的前10项3，5，7，9，11，…，21，求数列的通项”，仅有不足15%的教师能正确运用拉格朗日插值公式解释背后原理，其余教师只是通过观察猜想公式；“求一组组合数之和”，不足25%的教师揭示教材C0n+C1n+C2n+…+Cnn=2n赋值±1的内涵。

四、总结与建议

1.数学概念

“广度—深度”同步理解：数学概念本身具有高度的抽象性，对于概念教学，需要有意识地还原数学概念的数学化语言，即从学生理解的水平层次交代字面含义，结合“高观点”认知，最大化地为学生的概念学习提高广度，同时注意从具体简单到抽象复杂的逐步延伸，进而促进学生明确概念、纠正错误，避免元认知导向错误。

2.数学命题

“内修—教学”双向提高：要实现学生自我发现并创造数学知识，教师不应将整理好的证明直接提供给学生。教师自身的理解水平能够达到引导和帮助学生进行“再创造”，组织自然生成的教学，学生自主完成命题的发现与证明。

3.数学解题

“创造—再创”一以贯之：以往教学注重问题解决方法上的“再创造”，但其实问题的本身更应注意，如增添数学的为什么，探寻源问题的路上层层揭开数学的神秘之纱。另外，还可以跳出数学符号化，将文学艺术与数学符号或思想连通，在问题的根源实现“再创造”，丰富数学的问题形式和解题视角，增添趣味。

五、结束语

解释“数学概念”、证明“数学命题”、探究“数学解题”，无不告诉教师提高自身理解水平亟待加强，观点高了，才能看得深。另外，师范类院校数学专业的学生更要从入校起重视联系“高观点”对初等数学的指导，避免教学断层。