钢轨焊接接头不平顺演变条件下的轮轨接触分析

陈 嵘，孙耀亮，安博洋，王 平，阚前华

(1.西南交通大学高速铁路线路工程教育部重点实验室，成都 610031； 2.西南交通大学土木工程学院，成都 610031；3.西南交通大学力学与航空航天学院，成都 610031)

引言

由于焊接工艺的限制，钢轨焊接接头处容易出现短波几何不平顺，这会显著地加剧钢轨焊接接头区域的轮轨相互作用[1-3]。在轮轨接触荷载循环往复作用下，钢轨焊接接头处容易出现疲劳裂纹，严重制约着钢轨的服役寿命与行车安全[4-5]。

国内外学者对钢轨焊接接头开展了许多有价值的研究。KERR和COX等[6]对钢轨焊接接头进行了理论分析和试验研究，调查了车轮垂向荷载对无缝线路绝缘钢轨接头受力的影响。GROSSONI等[7]利用车辆轨道耦合动力学模型研究了钢轨焊接接头的动力特性，并分析了车辆和轨道参数对钢轨焊接接头处峰值力的影响。翟婉明等[8-9]建立了地铁线路焊接接头区轮轨动力相互作用模型，分析了钢轨焊接接头实测几何不平顺引起的轮轨动力响应特征，调查了不平顺波长波深、行车速度、轨下胶垫刚度和轨道结构形式等影响。STEENBERGEN[10-11]建立了考虑轮轨多点接触的动力学模型，分析了不同轮轨接触状态对钢轨焊接接头处轮轨冲击的影响，并建立了钢轨接头几何梯度、行车速度与动态接触力之间的定量关系，用以评估钢轨接头质量。安博洋[12]在STEENBERGEN方法的基础上提出了特征深度的概念，并利用三维轮轨瞬态滚动接触有限元模型模拟了高速铁路钢轨接头处的轮轨动力相互作用，进而建立了一种更为准确的钢轨接头质量评估方法。

上述研究侧重于模拟钢轨焊接接头处的车辆-轨道动力相互作用以评估车辆运行安全与平稳性，一些学者在此基础上利用有限元方法研究材料的响应。KABO等[13]研究了车轮通过钢轨接头时的动态响应，并对钢轨局部不平顺性、变刚度、接头处塑性变形和滚动接触疲劳进行了预测分析。为更为真实地模拟轮轨滚动接触，WEN等[14-15]建立了三维轮轨滚动接触有限元模型，采用弹塑性线性随动硬化模型模拟轮轨材料，并结合车辆-轨道耦合动力学模型分析了行车速度、轴重和轮轨材料对接头轮轨接触的影响。在此基础上，LI[16]建立了适用于分析曲线轨道的有限元模型，并引入Kalker的Fastsim算法以模拟轮轨切向作用，分析了钢轨接头不平顺对塑性变形的影响。MANDAL[17-18]建立了绝缘钢轨焊接接头的三维有限元分析模型，并基于弹塑性材料非线性运动硬化模型对钢轨材料响应进行分析，研究了绝缘钢轨焊接接头的低周疲劳和钢轨材料的棘轮特性。

从上述研究中可以发现，学者们对钢轨焊接接头的研究主要集中于车辆-轨道动态相互作用以及单次轮对通过后材料的弹塑性响应，对考虑钢轨接头实测几何不平顺演变条件下的轮轨动态相互作用及循环荷载作用下材料响应的研究则鲜有报道。这促使笔者开展钢轨接头不平顺演变条件下的轮轨接触分析研究，以期为钢轨接头养护维修提供理论基础。

1 模型介绍

为实现本文的研究设想，建立两类有限元模型，即三维轮轨瞬态滚动接触有限元模型和考虑材料循环本构关系的局部钢轨有限元模型。其中，三维轮轨瞬态滚动接触有限元模型用以模拟钢轨接头三维几何不平顺处的轮轨滚动接触行为，局部钢轨有限元模型则用以模拟循环接触荷载作用下材料的动态响应。

1.1 考虑实测钢轨接头几何不平顺的三维轮轨瞬态滚动接触模型

图1所示为建立的三维轮轨瞬态滚动接触有限元模型，模拟了我国某25 t重载线路的轮对-轨道系统。重载铁路直线段以轮对中心位于轨道中心并忽略摇头角的影响，为提高计算效率，该模型仅考虑半个轮对和半个轨道[19]。簧上质量简化成质点并通过弹簧和阻尼单元连接到轮轴。在建立有限元模型时，所建立的轨道长度为15 m，即25个轨枕间距，轨下离散支撑由扣件、轨枕和道床三层组成，每组扣件由18个弹簧和阻尼单元模拟，每个轨枕下的支撑采用15组分布的弹簧和阻尼单元表征。

图1 三维瞬态滚动有限元模型

该模型着重考虑了真实的轮轨几何形状，车轮踏面为LM型，钢轨采用CHN75轨并设置1∶20的轨底坡，轮轨均由8节点六面体实体单元模拟，网格尺寸为1 mm。采用基于罚函数法的面-面接触算法求解轮轨间的滚动接触行为。模型具体边界条件如下：轨道底部固结，轨道纵向端部约束纵向和横向位移，车轴外端部约束横向位移，轨道的对称面和车轴内端面施加对称边界条件，扣件只保留垂向自由度。该模型的单元和节点总数分别为1 070 391个和1 201 240个。更多模型细节和建模方法参见文献[12，16]。

为考虑钢轨接头几何不平顺的演变状态，采用铁科院获取的实测数据进行分析[20]。如图2所示测量数据取自轨顶中心线，共测量9次，间隔时间为1个月。由实测数据可知，第1次测量时焊接接头处存在明显的初始不平顺，在随后的4次测量中逐渐趋于稳定。由于钢轨磨损和塑性变形作用，焊接接头在热影响区域K1和K2处很容易形成马鞍形不平顺。第6次测量时发现钢轨接头不平顺的幅值相对较小，在随后的3次测量中发现钢轨接头不平顺急剧发展。

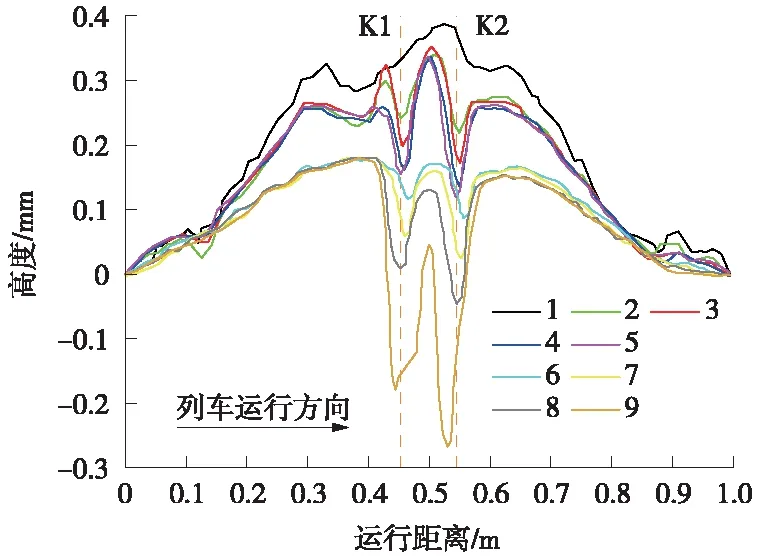
图2 重载线轨道接头不平顺演变过程[17]

上述钢轨接头几何不平顺通过修改模型对应的k文件实现，即利用所编程序修改相关单元的节点坐标，具体实现方法参见文献[12]。

1.2 考虑材料循环本构关系的局部钢轨有限元模型

1.2.1 钢轨模型建立

图3为所建局部钢轨有限元模型。钢轨长度取1 m，考虑到钢轨接头几何不平顺的影响区域，所施加移动荷载的网格细密区长度为200 mm。在钢轨纵向两端面施加纵向约束，钢轨底面则采用全约束方式。该模型的单元和节点总数分别为199 424个和221 713个。

图3 局部钢轨有限元模型

在局部钢轨有限元模型中，采用法向应力和切向应力在滚动方向上的平移来模拟循环滚动过程。考虑钢轨接头处的非稳态滚动接触情况，法向应力和切向应力均随时间变化，荷载历程取自1.1节所建三维轮轨瞬态滚动接触有限元模型动态模拟结果。钢轨表面的循环移动荷载通过自编程序修改inp文件实现，滚动方向如图3所示。在初始位置A点处，接触载荷通过10个增量步逐渐增加，随后接触载荷沿纵向逐步向终点B移动，接触荷载在一个增量步里移动距离为1 mm，滚动总距离为100 mm。经过100步滚动，接触斑到达B点，最后通过10个增量步减小至零。为节省计算成本又不影响计算结果，本文考虑5次荷载循环。

1.2.2 材料本构模型

钢轨接头区材料采用CHABOCHE线性各向同性随动硬化循环塑性模型(以下简称“CHABOCHE模型”)进行模拟，该模型能够合理地描述轮轨滚动接触条件下材料循环塑性应力松弛和棘轮效应[21]。

CHABOCHE模型基于Von Mises屈服准则建立如下公式

(1)

式中，σ为应力张量；α为背应力张量，即屈服面中心；s为偏应力张量；a为偏背应力张量，即偏应力空间中屈服面中心；k为屈服面尺寸，在该随动硬化模型中为常数。

为描述塑性流动，塑性应变沿屈服面梯度方向的增量为

(2)

式中，dεp为塑性应变率；dλ为塑性乘子；f为屈服函数。

硬化准则用来规定材料进入塑性变形后的后继屈服函数在应力空间中的变化准则[21]。CHABOCHE提出一种具有更多材料参数的运动硬化规则[22]。该模型硬化准则表述为

(3)

式中，Ci和γi为材料参数；dp为累积塑性应变率，将其定义为

(4)

模型中相关材料参数取自重载铁路常见的U71Mn[23]，见表1。

表1 CHABOCHE模型材料参数

2 结果分析

2.1 动态接触力

图4展示了第1、5、9三次实测几何不平顺条件下轮轨接触力随运行距离的变化。横轴是车轮滚过的距离，对应于图2中钢轨接头沿纵向的分布位置。从图4中可以发现，在车轮进入钢轨接头局部塌陷区之前，即运行距离小于0.35 m的区域，三种不平顺条件下的轮轨接触力波动幅值几乎保持一致，这说明波长较长的不平顺很难激发明显的轮轨冲击力。运行距离在0.35～0.7 m范围内时，轮轨法向力和切向力均出现了由接头局部塌陷引起的冲击现象。随后，车轮离开局部缺陷区域，轮轨接触力逐渐趋于平稳。

图4 轮轨接触力随运行距离变化情况

图5展示了钢轨接头不平顺演变过程中轮轨法向力和切向力最大值的变化情况。第1次实测不平顺条件下最大轮轨法向力为174 kN，随后逐渐增加到第5次测量的197 kN；由于第6次测量得到的不平顺较为平缓，其最大法向力减小到174 kN，在随后的3次结果中其最大值迅速增加到245 kN，约为静载荷的2倍。总的来讲，钢轨接头几何不平顺在前5次测量中主要表现为凸接头的形式，其几何不平顺幅值发展以及轮轨法向力的变化均较为缓慢；而后4次测量中，钢轨接头的凹型成分占据主导，因而发展更为迅速。

关于轮轨切向力的变化，其变化相对平稳。这主要是因为轮轨处于蠕滑状态，未达到全滑动，法向冲击力对切向的影响不明显。

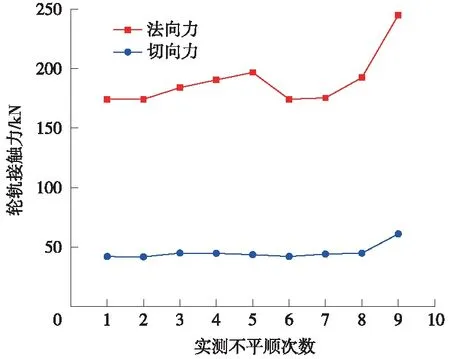
图5 轮轨接触力最大值变化情况

2.2 局部滚动接触解

图6展示了第1、9次实测几何不平顺条件下轮轨接触斑形状及黏滑分布的变化情况，图中包含了10个时刻的结果。为了在图中清晰地展示结果，对该10个时刻结果的横向坐标进行调整。第1次实测几何不平顺条件下，接触斑的形状和黏滑区比例在整个车轮滚动过程中保持相对稳定。虽然第1次实测几何不平顺的平直度最大，但其局部几何变化较为平缓，因而未能引起轮轨接触斑明显的变化。然而，接触斑形状和黏滑分布在第9次测量结果下出现了明显的变化，这是由局部几何不平顺和轮轨冲击力共同引起的。注意到，该不平顺条件下第2个和第6个时刻(对应图2中的两个局部凹陷)出现了近似全滑动的结果，这意味着这两处区域的钢轨材料极易出现明显的磨损现象，这是引起钢轨接头几何不平顺后期急剧变化的主要原因之一。

图6 两次实测不平顺的接触斑黏滑分布变化情况(蓝色代表滑动区，绿色代表黏着区)

图7和图8展示了最大法向和切向接触应力的变化结果。随着接头几何不平顺的演变，在K1和K2区域内接触应力逐渐增大。具体而言，法向接触应力最大值由第1次的1 220 MPa增大到第9次的1 630 MPa，切向接触应力最大值由第1次的447.2 MPa增大到第9次的501.5 MPa。

图7 实测几何不平顺条件下钢轨纵向不同位置处最大法向应力演变过程

此外，由图7和图8可以发现，局部接触应力的波形与接触力并不完全一致，这是因为局部接触几何形状的影响所致。以往研究中通常采用多体动力学求得钢轨接头不平顺处的宏观接触力，再作为输入条件利用基于半空间假设的接触模型(如CONTACT)求解轮轨接触解。这种分开求解的方法无法考虑真实的轮轨接触几何，会损失计算精度。因此，有必要建立一种耦合结构动力学和局部接触的有限元模型进行求解。

图8 实测几何不平顺条件下钢轨纵向不同位置处最大切向应力演变过程

2.3 应力-应变响应

为研究循环荷载作用下钢轨材料的响应情况，将滚动接触应力时程结果施加于局部钢轨模型。图9所示为实测几何不平顺演变条件下最大等效应力对应位置处的应力-应变响应，即考虑最不利的情况。可以发现，所关注的9个实测几何不平顺均会导致材料产生棘轮效应，塑性变形不断累积。

图9 等效应力应变响应曲线

相较前5次应变累积较为平缓的现象，后4次结果中塑性变形累积变化更为明显。具体而言，前5次末循环的累积应变由0.076增大至0.093，而后4次末循环的累积应变由0.079增大至0.121。累积应变变化率相应地由22.4%增大至53.2%。

上述结果分析中考虑了列车的牵引转矩，即轮轨界面存在较大的切向力。而列车在运行过程中还存在惰性工况，即不施加牵引/制动转矩。为此，在上述研究的基础上，考虑了无切向力工况下钢轨的应力应变响应。以第1次和第9次的结果为例，图10展示了无切向力情况下的等效应力-应变响应曲线。可以发现，无切向力工况下两个结果均处于塑性安定状态。由此说明，切向力的施加会显著改变材料的服役状态，破坏形式也会出现本质的差异。因而，为控制钢轨接头区的材料伤损现象，可通过优化列车牵引制动方式提高其服役寿命。

图10 无切向力情况下等效应力-应变响应曲线

3 结论

本文建立三维轮轨瞬态滚动接触有限元模型和考虑材料循环本构关系的局部钢轨弹塑性有限元模型，详细分析我国某线路实测钢轨焊接接头几何不平顺演变下的轮轨动力相互作用和材料动态响应。得出主要结论如下。

(1)随着接头几何不平顺的演变，轮轨动力相互作用愈发强烈。钢轨接头不平顺前期演变过程中，其激发的最大轮轨接触力的变化较为缓慢；而在中后期，其变化则较为迅速。

(2)钢轨接头不平顺发展前期轮轨接触状态变化较为平缓，随着不平顺的演变，接触斑形状及其接触应力分布急剧变化，是加剧几何不平顺发展的主要原因。

(3)考虑列车牵引工况时，在轮轨切向力的作用下，钢轨材料响应在接头不平顺演变中均处于棘轮效应状态。随着接头不平顺的演变，累积的变形逐渐加剧，即恶化速度加快。列车惰行工况下，钢轨材料响应因无切向力而处于塑性安定状态。可通过优化列车牵引制动方式控制钢轨接头区的材料伤损。