五轴数控机床在机测量探头补偿技术研究

葛英飞，张泽宇

（南京工程学院 机械工程学院，南京 211167）

0 引言

我国作为一个制造业大国，对于制造业的产品质量以及生产效率要求越来越高，所以检测是产品制造中的重要保证，目前离线式测量如三坐标测量机是最主要的测量方法之一。但是其设备价格昂贵，并且对检测环境要求极高，加工完成后对待测零件装卸的过程当中，因为需对其进行二次定位装夹，从而造成检测误差，降低检测效率[1]。在机测量技术完美地平衡了检测与生产之间的关系，在机床加工过程中可以与检测紧密联系起来，可根据检测结果继续指导完成加工，避免了二次装夹、找正。在机测量中高精度可接触式探头是在整个检测过程中最重要的一项工具，但是其测量精度受到不同因素的影响会给检测系统带来误差，所以在检测开始前要对探头进行标定以及半径补偿[2]。赵小军[3]提出利用Delaunay三角剖分思想，实现测头的半径补偿消除误差。徐丽丽[4]分别通过二维和三维的方法来实现半径补偿，虽然精度较高，但是该方法只适用于较简单的零件，具有一定局限性。Tibet Erkan等[5]通过迭代算法来分析其几何特征，并通过自己开发的软件补偿收集到的坐标数据。Givi[6-7]在Mir的实验基础上，通过Gauss-Newton法分析了误差了来源，使雅可比矩阵的补偿精度得到了改善。本文采用微平面补偿算法，通过实验分析引起五轴数控机床在机测量误差的原因，并完成探头的半径补偿，从而提升在机测量的检测精度。

1 探头半径补偿误差分析

1.1 在机测量工作原理

在机测量技术由于其成本低、检测效率高、无需二次装夹等优势被广泛用于零件加工测量当中，使得数控机床既是加工设备，同时又兼具测量功能。在机测量系统的构成如图1所示，硬件部分主要是由高精度探头、信号接收器、机床整个本体，软件部分由机床控制系统、测量软件等组成[8]。待零件加工完成后，数控机床会从其存储单元中读取待测零件的测量程序，从而从刀具库中调出测量探头，驱动测头开始检测。当主轴驱动测头缓慢向待测零件靠拢时，测头的红宝石球会与待测件的表面快速接触，此时其前端的测杆会发生微小的位移，测杆内部与弹簧接触产生电流，触发信号发出，然后通过其内部蓝牙传感器将此时记录下的主轴坐标传给信号接收器，测量程序会根据测头与待测件的位置关系，转换出待测件的位置坐标，最后机床停止进给，开始检测下一个测量点。由于待测件一直摆放在工作台上，待测零件坐标系与机床坐标系是重合的，如果加工几何参数检测不合格，可以借助在机测量软件实现加工与测量程序的共享与融合，进行后续的修正与补偿，最终给出检测报告。

1.2 机床探头预行程误差分析

在分析探头半径补偿原理之前，首先要分析引起误差的原因。引起探头误差原因主要有4个方面：探头结构误差、探头位姿误差、探头预行程误差及探头偏心误差。预行程为探头与待测件接触至产生触发信号测杆所移动的距离，探头的预行程对检测精度有着很大的影响。如图1为探头触发过程图，图2为探头触发时序图，两张图的运动过程彼此对应。

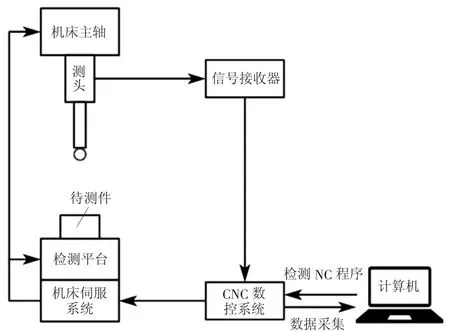
图1 在机测量原理结构图

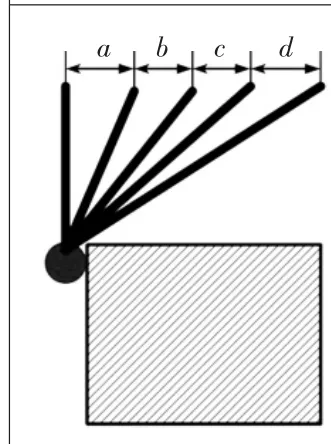
图2 探头触发过程图

探头触发时序图如图3所示。

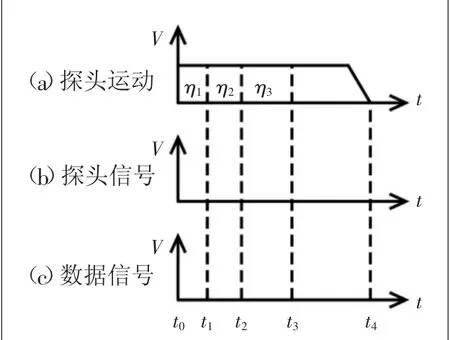
图3 探头触发时序图

t0-t1（对应图2中的a）：此阶段为探头预行程，即探头与待测件接触至测头发出触发信号的时间滞后；

t1-t2（对应图2中的b）：此阶段为接口响应时间，即探头发出接触信号至数控机床的信号接收器的时间滞后；

t2-t3（对应图2中的c）：此阶段为控制器响应时间，即机床储存接收到的坐标数据的时间滞后；

t3-t4（对应图2中的d）：此阶段为减速距离，即检测完成主轴驱动探头驶离测量点。

从上述4个阶段可知，从探头触发信号到机床记录储存下坐标数据的过程中，探头在极短的时间内仍会以触发前的速度移动微小的距离，这段距离即为预行程误差，该误差大小可以表示为

由式（1）可知，预行程误差大小与探头进给速度，以及探头接触待测零件至机床记录下探头所测坐标数据时间有关，当v越大时η越大，当v过大时会导致t4阶段预行程误差过大，但是当v过小时探头的信号触发时间会过长，从而降低检测效率。所以为探头选择合适的进给速度对在机测量的检测效率以及检测精度尤其重要。另外，由式（2）、式（3）可知测杆刚度、逼近距离、探头直径等方面同样对预行程误差产生影响。

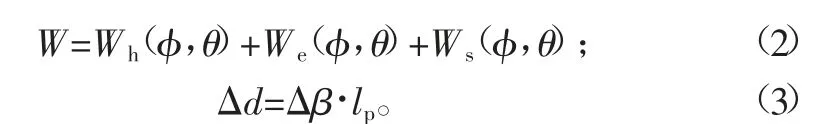
式中：Wh为测量机测杆的弹性变形；We为探头与待测零件接触时所产生的形变；Ws为测杆位移；Δd为瞄准误差；φ、θ分别为探头在红宝石球下的方位角和极角；Δβ为测杆的偏转角；lp为测杆的有效长度。

1.3 机床探头位姿误差分析

由1.2节分析可知，探头的移动速度对探头的预行程误差有着重要影响，但是探头的位姿状态同样对测量产生着影响，因为探头在与待测件接触时获得的是探头的球心坐标，此时应尽量保证探头球心的法矢方向、探头的运动方向、测量点的法向方向保持一致，并且探头的运动速度也要和半径补偿时的速度保持一致，如果这两点要求不能满足，在测量时会产生不同矢量方向的误差。经实验总结归纳，在探头测量过程中主要有以下4种方位。

如图4所示，当探头的运动方向为竖直向下时，待测件的平面为倾斜的，当探头与待测件的平面接触时实际接触点为点A，此时探头获得的坐标值为O点，经半径补偿后获得的是B点的坐标值，但是理想测量点C与实际测量点A并没有重合，理想测量点C 与补偿后数据点B 相差的距离为dr。如图5所示，探头的运动方向与待测件所接触点的法矢方向保持一致，此时探头经半径补偿后所得到的r是准确的，可以正确获得A点所在位置，为了减少预行程所带来的误差此时探头不需要摆角。

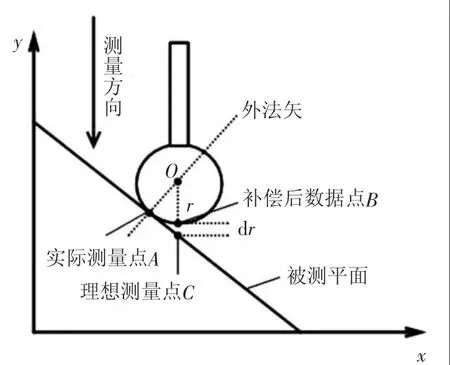
图4 探头补偿示意图1

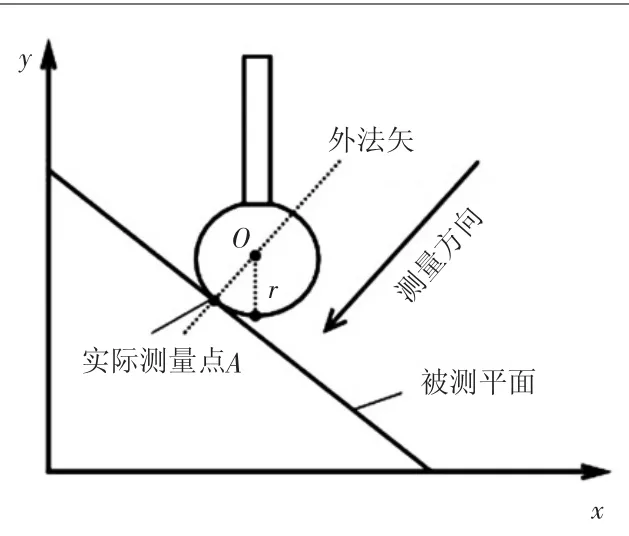
图5 探头补偿示意图2

如图6所示，当待测平面为曲面时，如果待测点所在的曲率半径大于探头的半径，当探头与待测平面接触时，待测点与接触点两点法矢方向保持重合，此时所获得的补偿半径也是准确的。

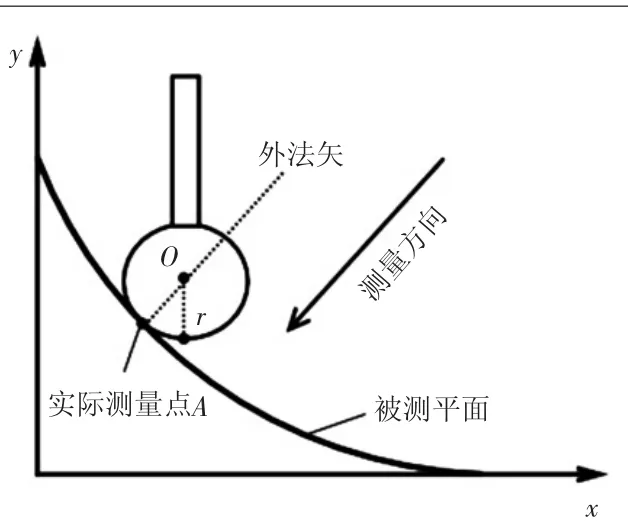
图6 探头补偿示意图3

如图7所示，此时探头以一定的摆角向待测零件运动，此时实际接触点与理想接触点的法矢方向重合，此时经半径补偿后所获得的坐标值仍是准确的。

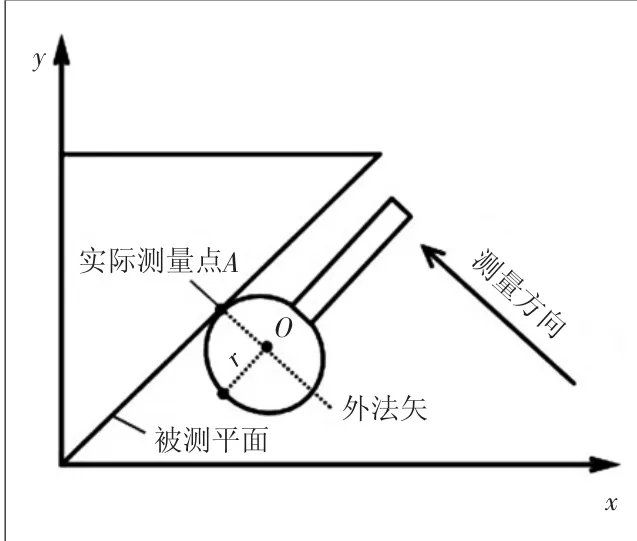
图7 探头补偿示意图4

2 探头半径误差补偿

2.1 探头标定补偿的必要性

由于探球的物理特性的原因，在实际测量中我们需要将考虑到所有引起误差的因素，所以在测量前对探头进行标定补偿是必要的。图8所示为探球球心运动轨迹示意图，其轨迹为与待测件接触表面相差探球半径r的包络线，在探球运动的过程中，机床所获得的是球心O的坐标值，测量软件在补偿时将自动处理数据并加上探球的半径作为实际测量值，但是此时因探头的机械惯性该测量值是一个动态值，考虑到在1.2节中讨论的预行程误差，探头所获得坐标值以及机床实际所获得的坐标值过程中，探头在空间内会产生极小的位移，该位移虽小但其对测量的准确度有着重要影响，所以探头的标定补偿就是使探头在测量时的任意法矢方向上获得准确的测量坐标值。

图8 探球球心运动轨迹示意图

2.2 探头半径补偿算法实现

为了准确地获得测量值，在对探头进行半径补偿时，我们可以通过解析函数来分析所测坐标值，即通过解析的方法来获得所测点的准确法向，通过法线的方向我们可以准确地获得探球球心的运动轨迹。在测量曲面时需用到三维曲面法向，故本实验对于探头补偿将采用微平面法来实现。当空间内存在4个不共面的点时，可以确定唯一一个不共面的球，如图9所示，在测量点P（x，y，z）附近，近似地认为某块极小区域为一球面，所取的P1（x1，y1，z1）、P2（x2，y2，z2）、P3（x3，y3，z3）、P4（x4，y4，z4）通过最小二乘法拟合出最佳平面，并通过4点法线的交点即可确定球心所在位置，因为在测量时所测点云极为密集，所以当所取的4个点无限趋于接近时，我们就可以利用这4个点来求解所测点的法矢，其计算方法为

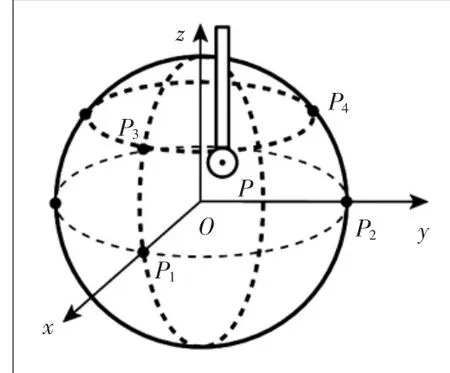
图9 微平面法求曲面法向

通过对上述数值进行单位化处理，所得单位法向矢量即为被测点的法相矢量，经补偿后，求得实际接触点P（x，y，z）的坐标值为

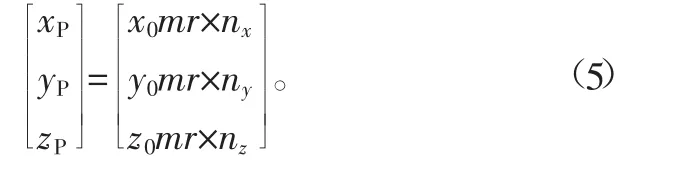
式中，O（x0，y0，z0）为球心坐标。

根据上述方法补偿后的点拟合而成的曲面就是最终的测量曲面，需说明的是,上述测量中所用到的是探头所测得的O1、O2、O3、O4的球心坐标值，通过这4点来拟合曲面，并通过该曲面法向实现补偿。

3 探头补偿实验验证

由2.2节可知该算法适用于复杂的曲面测量，在测量点极多的情况下，进行微平面的多点网格化处理更加简单实用，本实验将基于拓璞C100P五轴数控机床，使用RenishawRMP60接触式探头，红宝石测头半径为5 mm，对直径为50 mm的标准球进行测量实验。本实验将对标准球进行分层测量，每层相隔22.5°，并且在每个圆周上平均地测量8个点，记录下此时的测量值，共测量48个点。

本探头的红宝石球半径为3 mm（如图10），从上述试验结果可以看出,在整个实验测量，其测量半径均小于理想半径，造成这个结果的原因是因探头在测量过程中预行程所引起的误差，即验证了1.2节的分析。与此同时从表1可以看出，随着测量角度的增大，测量半径随之减小，这是因为随着探头的摆角增大，实际测量点与理想测量点之间的dr增大，故而半径r随之减小。

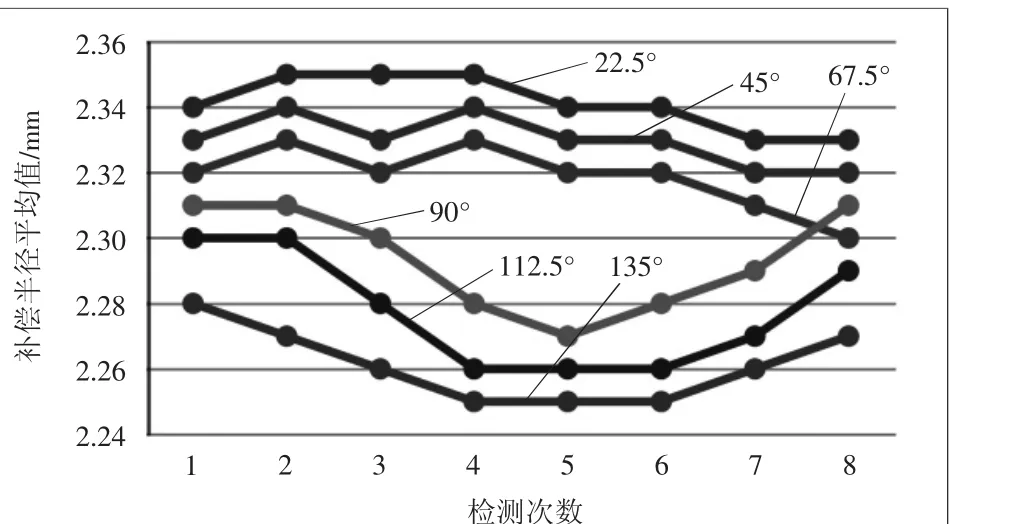
图10 补偿前测量结果

如图11所示，该实验结果是在上一次获得的测量结果的情况下，结合微平面补偿算法得到的最终测量结果，在此基础上与标准球的理论值进行比较。经过计算,在半径补偿后，误差最大值为0.013 mm，误差最小值为0 mm，几乎与理论值相符。从表1可看出补偿后的探头半径与实际值比较相符，验证了补偿算法的可靠性。

表1 平均补偿半径

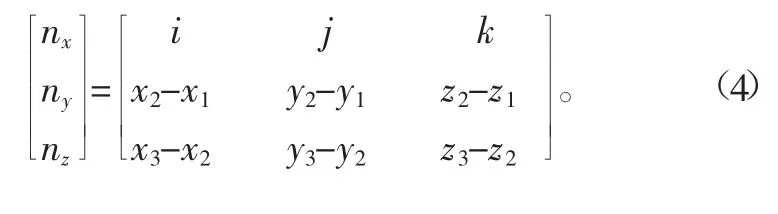
综上分析，计算补偿前所测得的48组数据的半径大小的偏差值，取绝对值，相加平均得出其测量误差为0.196 25 mm，经计算补偿后的补偿半径误差为0.001 625 mm，可以看出经半径补偿后测量精度有着显著的提高，此算法为后续在机测量技术的研发奠定了基础。

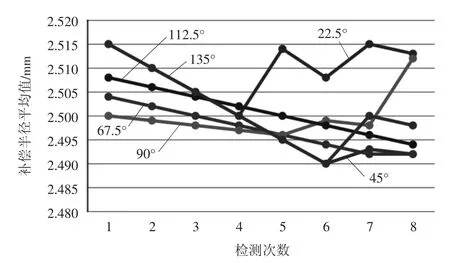
图11 补偿后测量结果

4 结语

为了提高在机测量的检测精度，本文从探头检测过程中的预行程以及位姿状态等角度出发，分析了检测误差的主要来源，提出了通过对探头的半径补偿标定来降低测量误差。通过建立数学模型以及利用数学函数解析的方法，提取出待测点的坐标值，与微平面算法结合，通过最小二乘法拟合出理想测量平面的方法，对任意法矢方向的测量进行半径补偿。经实验验证，在对补偿前后所测量48组数据进行分析，其测量精度得到显著提升，测量误差可以达到0.001 625 mm，说明该半径补偿方法对于在机测量技术的提升是有效的。