立式重载储能飞轮转子动力学特性分析

周传迪，柳亦兵，朱万程，高峻泽，张昊随

(华北电力大学 先进飞轮储能技术研究中心，北京 102206)

0 引 言

飞轮储能系统以其功率密度高、充放电速度快、无污染等优点在解决新能源电力系统的不稳定性和电网的变频调速等方面备受关注[1-3]。由于储能需求的增加使得飞轮储能系统的设计储能量大幅提高，进而导致飞轮的体积、重量和工作转速有了非常大的提升，使得飞轮转子的临界转速不可避免地落在工作转速范围内[4]，导致飞轮产生较大的振动。因此，有必要准确预测飞轮转子-轴承系统的动态特性，以避免飞轮系统工作在临界转速附近，减少共振。

为了探索飞轮转子-轴承系统的动力学特性，许多学者建立了飞轮转子-轴承系统的动力学模型并进行了动力学特性分析。C.Tang[5，6]等建立了柔性支承的飞轮转子-轴承-阻尼器的动力学模型，并计算了其在不同转速下的动力学特性。C.peng[7]建立了磁悬浮飞轮的微振动动力学模型，包括转子动力学、磁悬浮轴承控制系统，并对系统的微振动进行了研究。H.Wang[8]利用拉格朗日方程建立了具有混合轴承支承的储能飞轮系统的动力学模型，计算了飞轮系统的动态特性。研究表明，飞轮转子由于转速较高，在通过临界转速时会产生较大的振动，为了解决这一问题，利用阻尼抑制飞轮转子振动的方法越来越受到重视。阻尼器的类型包括挤压油膜阻尼器[9-13]、摆锤调谐质量阻尼器[14，15]和阻尼动力吸振器[16]等。通过相关研究表明，阻尼器能有效地降低飞轮转子的振动。使转子更好地通过临界转速。对于电磁轴承支承的飞轮转子，通过调整刚度、阻尼等控制参数[15,17，18]和控制算法[19，20]同样也可以抑制飞轮振动，效果显著。

上述研究中，飞轮转子普遍质量较小，多数都在百公斤级以下，以小型刚性飞轮转子为主。随着储能需求的增加，飞轮转子的重量和转速都逐渐增加，由于其重量大、转速高，结构轴向尺寸大，导致飞轮转子成为柔性转子，而且其电机转子部分的质量和刚度效应往往不可忽略，对动力学模型的精确性要求较高，其振动特性还需进行探究。本文针对某立式重载储能飞轮转子-轴承系统的动力学建模问题进行研究，加入电机转子部分的质量，建立飞轮转子-电机转子-轴承系统的动力学模型，并分析轴承支撑刚度、阻尼以及飞轮升速速率对飞轮转子振动特性的影响，为飞轮转子的动特性分析和振动抑制提供一定参考。

1 储能飞轮系统结构简介

图1所示为某立式重载飞轮转子系统结构示意图，其主要结构有上机械轴承、永磁轴承、飞轮转子、电机转子、电机、下机械轴承及飞轮外壳等。飞轮转子由永磁轴承在轴向进行承载，保持转子处于稳定悬浮状态。转子上下两端通过机械轴承支撑，承担径向载荷。双向电机位于飞轮下部，电机转子嵌套于飞轮转子轴段上。飞轮系统的部件全部置于飞轮外壳中，由真空泵将内部空气抽出形成真空环境以降低损耗。

图1中所示的飞轮转子重量集中在飞轮转子本体以及电机转子两部分，且飞轮转子的重量与电机转子的重量相差较大。由于电机转子嵌套于飞轮转子细长轴段上，与飞轮转子下部轴段紧密连接，因此在建模时需要考虑电机转子质量及其刚度带来的影响[21]。

图1 飞轮结构示意图Fig.1 Schematic diagram of flywheel structure

2 飞轮转子-轴承系统动力学建模

2.1 飞轮转子-轴承系统动力学模型

采用集中质量法，基于以下假设建立了如图2所示的飞轮转子-电机转子-轴承系统的动力学模型：

(1)只考虑了转子的横向振动。

(2)飞轮转子本体部分视为具有集中质量的刚体。

(3)飞轮转子的细长轴段是柔性的，将其视为无质量的弹簧。

(4)考虑了电机转子部分的质量和刚度。

(5)轴承简化为具有集中质量、刚度和阻尼系数的线性结构，且是各向同性的。

(6)转子不平衡量假设均匀分布于转子上下表面。

飞轮转子、电机转子及上下机械轴承均简化为相应的集中质量，图中m1、m5分别为上机械轴承和下机械轴承的质量，m、m4分别为飞轮转子和电机转子的质量。k1、c1分别上机械轴承处的刚度和阻尼，k5、c5分别下机械轴承处的刚度和阻尼。k2为飞轮转子上部轴段刚度，k3为电机转子上部轴段刚度，k4为电机转子下部轴段刚度。

转子转动过程中由于受到不平衡力和力矩作用，转子会发生偏转，其各点的运动位置关系如图2所示。图中x1、x5分别为上轴承和下轴承质量点位置坐标，x2、x3分别为飞轮转子本体部分上下端中心点坐标，x4为电机质心位置坐标，xc为转子形心的位置坐标，xe为转子质心的位置坐标，偏心距为e，θy为转子在xoz平面的转角。转子为轴对称结构，转速为ω，转子的赤道转动惯量为Jd，极转动惯量为Jp。转子在yoz上的各坐标位置可参考xoz平面的坐标位置，在此处不再列出。

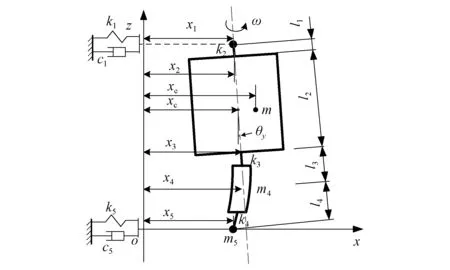
图2 飞轮转子动力学简化模型Fig.2 Simplified model of flywheel rotor dynamics

2.2 飞轮转子-轴承系统运动方程

对图2所示的飞轮转子采用拉格朗日法建立转子系统的运动方程，第二类拉格朗日方程如下：

(1)

飞轮转子在转速ω为定值状态下，动能，势能以及损耗能分析如下。

(1)动能T：

由图2可得转子形心坐标(xc,yc)与质心位移坐标(xe,ye)的关系如下：

(2)

在小振动情况下，由图2(b)可得

(3)

假设转子本体的动能为Tz，轴承系统动能为Tb，电机转子动能为Tr。则飞轮转子-轴承系统的总动能为

T=Tz+Tb+Tr=

(2)势能U：

飞轮转子-轴承系统的总势能为

(5)

(3)耗散能Z：

飞轮转子-轴承系统总耗散能为

(6)

(4)外力Q：

转子稳态运动状态，转子上的外力为零，即

Q=0

(7)

将式(4)、(5)、(6)、(7)代入式(1)，得到飞轮转子-轴承系统的稳态涡动方程为

写成矩阵形式：

(9)

(10)

m2=m/4+Jd/l22,m3=m/4-Jd/l22

(11)

式(9)为飞轮转子-轴承系统的稳态涡动方程，可以求解得到飞轮转子-轴承系统的稳态响应。

在飞轮充放电过程中，由于转子转速会随时间发生变化，此时ω是随时间变化的变量，不再是定值，因此需要推导转子的瞬态涡动响应方程。

(12)

将式(12) 代入式(4)、(5)、(6)，并将(4)、(5)、(6)代入式(1)中，整理可得飞轮转子-轴承系统的瞬态涡动方程为

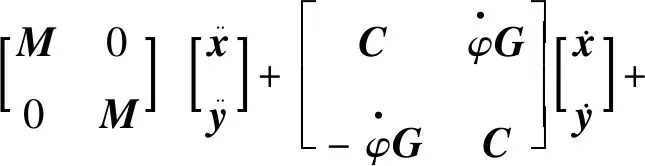
(13)

其中：

(14)

由式(13)可以求解得到飞轮转子-轴承系统的瞬态响应。

3 飞轮转子-轴承系统动力学特性分析

以图1所示的大容量飞轮储能转子系统为对象进行动力学特性建模分析，根据转子结构尺寸，利用三维建模软件Solidworks建立转子模型，计算转子的质量、转动惯量、轴段刚度等精确参数，参考文献[22]中的方法，先设定了轴承的支撑刚度和阻尼的取值范围，并根据实测数据进行了调整，最终得到各参数取值列于表1。

表1 飞轮转子-轴承系统各参数值Tab.1 Parameters of flywheel rotor-bearing system

3.1 临界转速分析

图3所示为飞轮转子系统的坎贝尔图。图中所示曲线分别为飞轮转子前两阶正反进动固有频率随转速变化曲线以及转子转速曲线。由于转子陀螺效应，导致转子固有频率随转速而变化，其中正进动曲线随转速增加而增大，反进动曲线随转速增加而减小。飞轮转速曲线在飞轮转子工作范围内与4条进动曲线共有4个交点，然而由于转子在实际转动过程中，不平衡量始终与转子同向旋转，因此转子的实际临界转速应为转速曲线与飞轮转子正进动曲线的交点。从图3所示的坎贝尔图中可以得到飞轮转子的一阶临界转速为1 900 r/min，二阶临界转速为7 300 r/min。飞轮转子在充放电过程中，转速在最低(3 000 r/min)和最高工作转速(10 000 r/min)之间不断变化，需要经常经过第二阶临界转速，因此第二阶临界转速对转子动力学特性影响较大，需要重点关注。

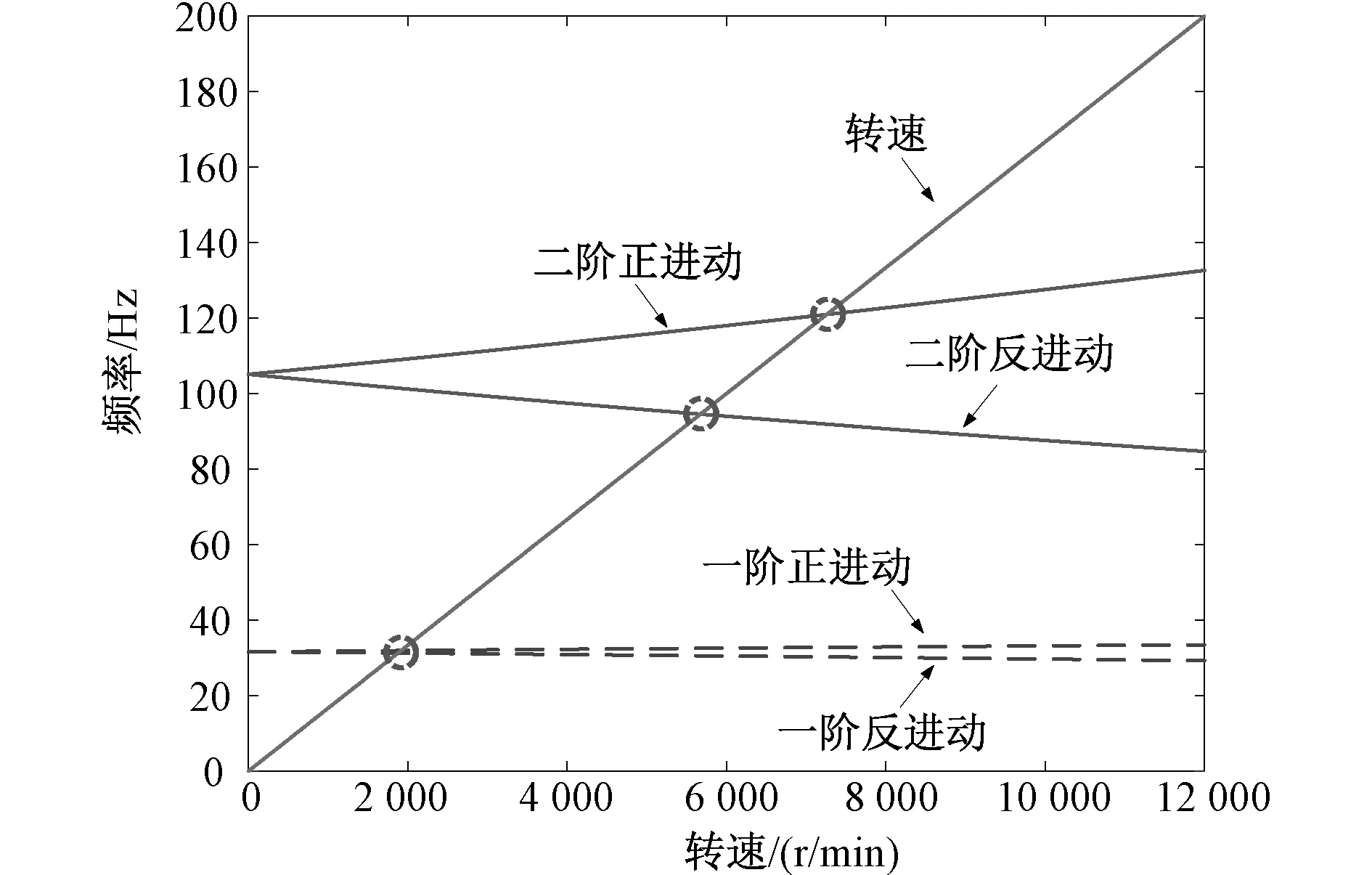
图3 飞轮转子坎贝尔图Fig.3 Flywheel rotor campbell diagram

3.2 轴承支撑刚度对转子振动特性的影响

为探究轴承刚度对飞轮转子动力学特性的影响，将上下轴承刚度在0.5e9～3e9 N/m范围内取不同值，计算转子稳态振动响应。图4和图5以瀑布图形式分别示出飞轮转子上下轴承处的频响函数曲线随轴承刚度变化情况。可以看出，飞轮转子频响函数曲线有两个峰值，分别对应飞轮转子的第一和第二阶临界转速。

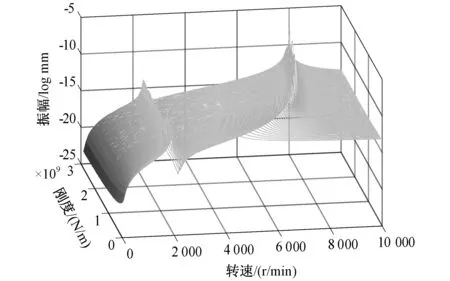
图4 上轴承处振动响应随刚度变化情况Fig.4 Vibration response at the upper bearing changes with stiffness

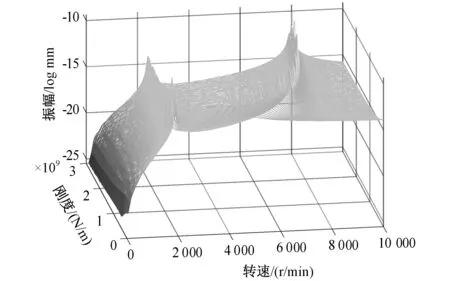
图5 下轴承处振动响应随刚度变化情况Fig.5 Vibration response at the lower bearing changes with stiffness

图6示出飞轮转子两阶临界转速随轴承刚度变化曲线，可以看出，随着轴承刚度增加，飞轮转子临界转速逐渐增大，当刚度较小时，两个临界转速增加较为明显，当刚度增大到一定程度以后，临界转速的增加速度变缓。

图6 飞轮转子临界转速随刚度变化曲线Fig.6 Critical speed of flywheel rotor changes with stiffness

图7示出飞轮转子过临界时，上下轴承处的共振幅值随轴承支撑刚度的变化情况，可以看到，随着刚度增加，上下轴承处共振幅值出现高低交错的波动现象，在某些刚度下，幅值达到最大值，在某些刚度降到最小，而且波动周期不是定值。这种现象表明，轴承刚度在一定范围的调整，可以改变转子的动刚度，降低转子系统振动。

图7 飞轮转子临界转速对应峰值随刚度变化曲线Fig.7 Critical speed of flywheel rotor corresponds to peak value versus stiffness change curve

3.3 轴承阻尼对转子振动特性的影响

为探究轴承阻尼对飞轮转子动力学特性的影响，将上下轴承阻尼在1 500～1e6 Ns/m范围内取不同值，计算飞轮转子稳态振动响应。图8和图9示出飞轮转子上下轴承处的频响函数曲线随轴承阻尼变化的瀑布图，图10和图11为两个临界转速及其共振幅值随轴承阻尼变化关系曲线，可以看到，在文中所计算的阻尼范围内，两阶临界转速随阻尼的变化而有小幅度改变，在阻尼范围为1 500～2e5 Ns/m区间内，阻尼对系统临界转速影响较小，两阶临界转速改变不明显，在阻尼范围为2e5～1e6 Ns/m区间内，第二阶临界转速相较于第一阶临界转速变化明显。此外，共振幅值随着阻尼的增大而呈明显的下降趋势，说明轴承阻尼对飞轮转子轴承处的振动具有抑制作用，且当阻尼较小时，振动幅值下降较为明显，当阻尼增大到一定程度时振动幅值下降变缓。

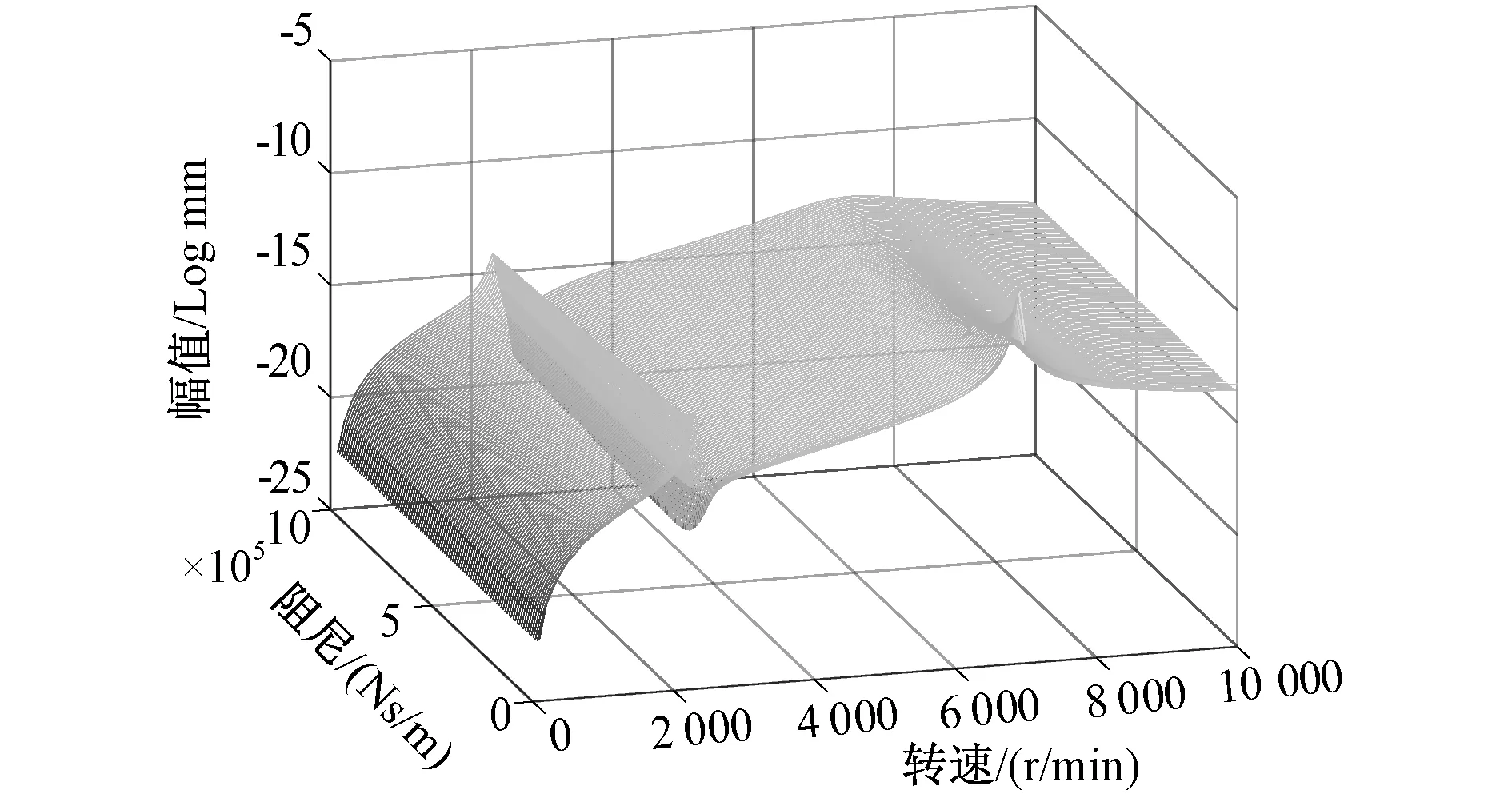
图8 上轴承处振动响应随阻尼变化情况Fig.8 Vibration response at the upper bearing changes with damping

图9 下轴承处振动响应随阻尼变化情况Fig.9 Vibration response at the lower bearing changes with damping

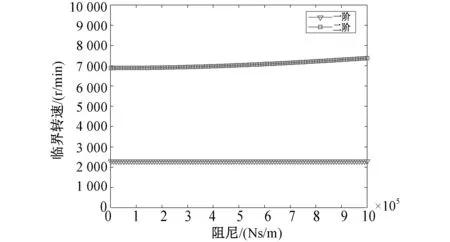
图10 飞轮转子临界转速随阻尼变化曲线Fig.10 Curve of the critical speed of flywheel rotor with damping

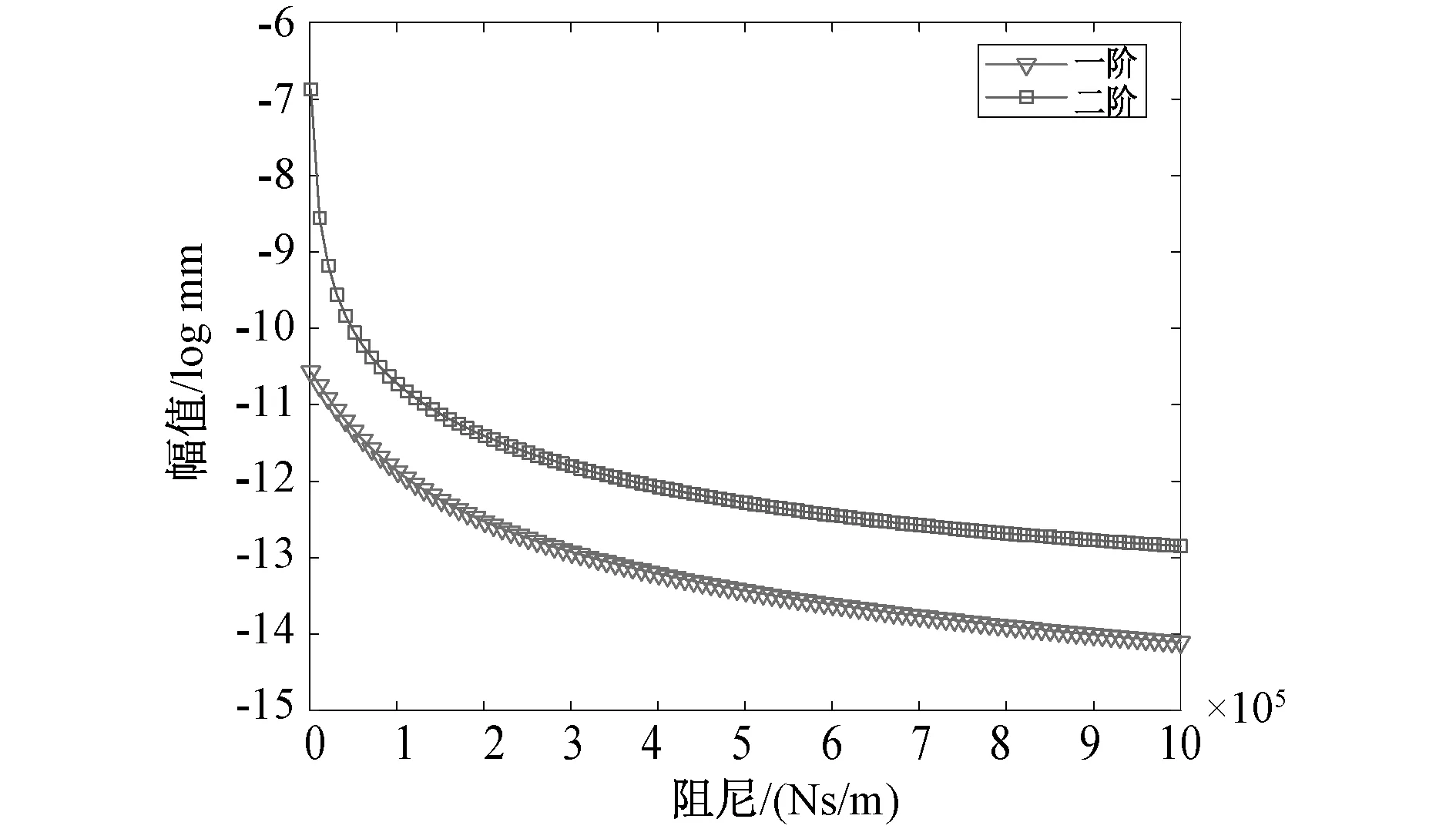
图11 飞轮转子临界转速峰值随阻尼变化曲线Fig.11 Curve of the critical speed peak of flywheel rotor with damping

3.4 升速速率对升速瞬态响应的影响

飞轮储能系统通过飞轮转子升降转速实现动能的存储和释放，因此在运行过程中，转速可能反复通过临界转速，为了避免转子在通过临界转速时产生较大振动，可以通过使飞轮转子快速通过其临界转速来达到降低振动的目的。本节分析飞轮转子在不同升速速率下的振动响应的变化情况，为飞轮转子如何通过临界转速提供理论依据。

对飞轮转子的瞬态涡动方程进行求解，参数取表1所列参数，计算得到飞轮转子在不同升速速率下的振动响应情况。共计算了4种升速速率下的飞轮转子振动响应，升速速率分别取2π rad/s、5π rad/s、10π rad/s以及20π rad/s。图12示出不同升速速率下飞轮转子上轴承处的振动响应幅值曲线，图13示出了飞轮转子通过临界转速时的共振峰值大小变化趋势，图14示出了飞轮转子临界转速变化趋势，可以看出，当转子以低速率升速时，过临界的振动幅度较大，当转子升速速率提高时，转子过临界振动幅值明显减小，而临界转速略有增大。分析表明，通过提升转子升速速率，可以在一定程度上降低转子过临界的振动幅度。

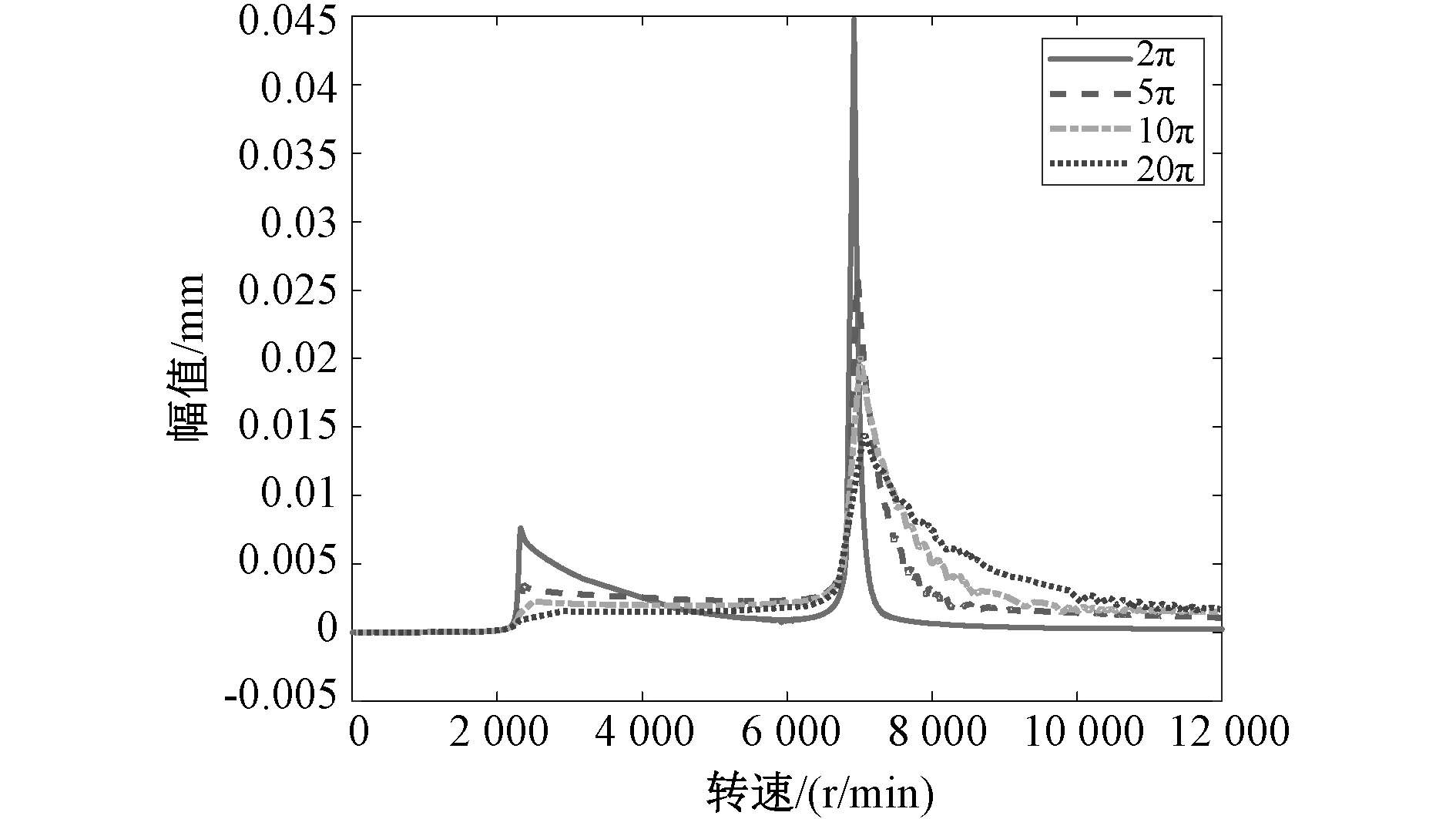
图12 飞轮转子不同升速速率下的振动响应Fig.12 Vibration response of flywheel rotor at different speed-up rates

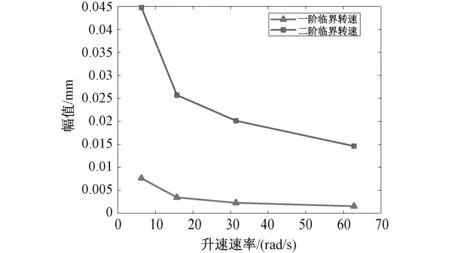
图13 飞轮转子共振峰值随升速速率变化曲线Fig.13 Curve of resonant peak value of flywheel rotor with speed-up rate

图14 飞轮转子临界转速随升速速率变化曲线Fig.14 Critical Speed of flywheel rotor variation curve with speed up rate

3.5 实验验证

为掌握飞轮系统的运行特性，并验证文中建立的飞轮转子动力学模型的合理性，对大容量储能飞轮转子系统进行升速试验。在飞轮转子外壳的上轴承和下轴承位置各放置一个振动传感器，用于测试升速过程中飞轮转子上下轴承处的振动情况。升速过程从转速为0开始，直至升速到10 000 r/min结束。

图15示出升速过程中的轴承振动响应幅值变化趋势，从图中可以看出，在升速过程中，上下轴承处均有三个较为明显的共振峰，对应转速分别为1 712 r/min，2 661 r/min以及7 336 r/min。与图12数值计算结果相对比，数值计算结果与飞轮转子实测结果基本符合，略有差异。飞轮数值计算结果在转速4 000 r/min以内范围内有一个共振峰，而实际测试结果有多个共振峰，分析原因可能是飞轮升速实测过程中传感器安装于飞轮外壳上，测得的数据受到飞轮外壳和其他部件的影响，从而在该转速范围内产生了共振所致。

图15 飞轮转子实测升速振动响应曲线Fig.15 Flywheel rotor actual measured speed-up vibration response curve

4 结 论

本文建立了立式重载飞轮转子的动力学模型，对飞轮转子动力学方程进行了动特性参数求解，获得了飞轮转子的固有频率、临界转速以及升速过程的响应曲线。通过分析轴承支撑刚度、阻尼以及飞轮转子升速速率对飞轮转子动力学特性的影响，可以得出以下结论：

(1)本文研究的大容量储能飞轮转子在0～10 000 r/min转速范围内存在两阶临界转速，与飞轮转子实际振动测试所获取的结果相一致，表明建立的飞轮转子-轴承系统动力学模型较为合理。

(2)飞轮转子的临界转速随着轴承支撑刚度的增大而增大，当支撑刚度增大到一定程度时，临界转速增加缓慢；飞轮转子过临界时的共振幅值随刚度增加出现波动现象，在某些刚度下出现极值；飞轮转子临界转速随轴承阻尼的改变而略有变化，但是飞轮转子振动幅值随阻尼的增大呈减小的趋势。

(3)通过改变飞轮转子的升速速率可以改变飞轮转子振动响应的幅值大小，升速速率越快则飞轮转子的振动响应幅值越小，因此在飞轮转子通过临界转速时可考虑通过控制策略提升转子的升速速率，进而降低飞轮转子过临界时产生的振动，使飞轮转子稳定运行。