C4F7N/CO2混合气体中粗糙度对环氧树脂表面闪络特性的影响

律方成，宋景萱，宋曼青，朱玫盈，张亚辉，路修权，谢 庆

(1.新能源电力系统国家重点实验室(华北电力大学)，北京 102206；2.输变电设备安全防御重点实验室(华北电力大学)，河北 保定 071003；3.国家电网福建检修公司，福建 福州 350013)

0 引 言

环氧树脂由于其优异的绝缘性能，常用于电气设备的绝缘[1-3]。然而，在直流电场作用下，绝缘材料表面容易发生电荷积聚，尤其是在高压设备中[4-6]。因此，抑制电荷积聚引起的表面闪络，提高环氧树脂的直流绝缘性能具有重要意义。

固体绝缘介质的表面特性是影响材料沿面绝缘性能的关键参数。一些学者提出了物理或化学方法改性方法来处理绝缘材料的表面，以改变闪络特性[7-10]。最近有研究表明，表面粗糙度处理是简单有效的方法。研究者们发现，较大的表面粗糙度可以抑制二次电子发射雪崩，且表面粗糙度是决定电荷积累量的有效因素之一[11，12]。对于环氧树脂材料，可借助机械打磨、涂层涂覆等手段对其进行表面粗糙度的调控，从而实现抑制电荷的积累，改善闪络性能的效果[13，14]。

目前，针对表面粗糙度-电荷行为-沿面闪络特性三者关联关系的研究大多数停留于现象记录与规律获取层面，仿真计算、机理研究鲜见；同时，随着用于替代SF6的混合气体C4F7N/CO2[15，16]逐渐推广，表面粗糙度改性策略能否在新型环保气体中发挥效用亟待实验验证[17-20]。

针对上述问题，本文基于有限元方法建立了表面电荷行为仿真模型，计算了粗糙度对环氧树脂表面电荷特性[21]的影响规律，从沿面电场强度、理论陷阱分布的角度，分析了粗糙度引起表面闪络电压变化的原因。并在C4F7N/CO2混合气体中开展了粗糙度改性环氧树脂材料的直流闪络实验，获得了粗糙度对闪络电压的实验影响规律，验证了仿真结果的合理性。

1 表面电荷模拟

1.1 主模型和子模型的建立

本文建立了环氧树脂表面电荷转移的二维模型。由于环氧树脂表面粗糙度是微米级的，因此，采用主模型和子模型两个不同尺度的模型研究了环氧树脂电极附近的表面电荷运动。在主模型中，手指型电极由不锈钢制成，直径为10 mm；两个电极之间的距离为10 mm。环氧树脂试样厚度为5 mm，长度为50 mm。对手指型电极施加1 kV的直流电压，由于电极附近表面电荷积聚较多，对表面电荷分布的影响最大，因此子模型关注电极附近的500×1000μm局部空间，引入高斯随机粗糙面来模拟环氧树脂的表面的微观特征。图1(a)和(b)分别为主模型和子模型。

1.2 无填料的子模型

首先考虑的是子模型中没有掺杂填料的情况，考虑了4种粗糙度，分别为Ra=0.3μm、0.8μm、1.3μm和2.2μm。区域P表示高压电极附近；区域G表示接地极附近。粗糙度Ra=0.3、0.8、1.3和2.2μm分别被命名为子模型P0、P1、P2、P3和G0、G1、G2、G3。主模型以及子模型G0、P0的电场分布如图1(c)和(d)所示。子模型的平均电场幅值为2.13×105V/m，主模型平均电场幅值为2.07×105V/m，比值接近1，说明子模型P/G建立的合理性。

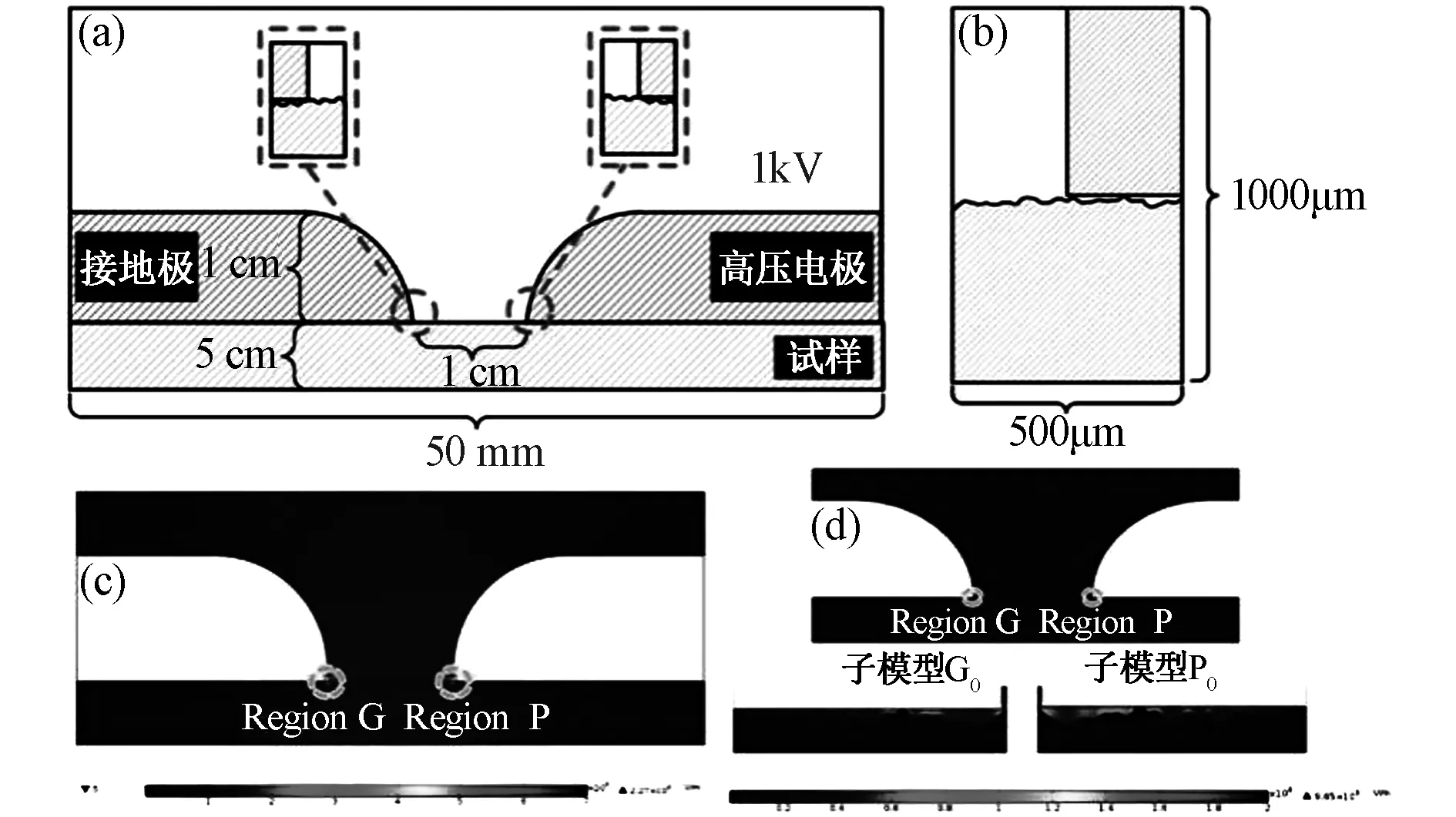
图1 主模型(a)和子模型(b)以及相应的电场分布(c)和(d)Fig.1 Main model (a),sub-model (b) and corresponding electric field distribution (c) and (d)

不同子模型的表面电荷密度和最大电场强度幅值如图2所示。负电荷在高压电极附近环氧树脂表面积累，正电荷在接地极附近环氧树脂表面积累。通过图2可以看出，随着粗糙度的增大，平均表面电荷密度和最大电场强度幅值均呈现先减小后增大的趋势。

图2 子模型P/G的表面电荷密度和最大电场幅值Fig.2 Surface charge density and maximum electric field amplitude of sub-model P/G

聚合物材料在运行中发生的物理老化和化学老化导致缺陷[22]，载流子陷阱与空间电荷积累密切相关[23]。表面粗糙度的深度为微米级，可能引起材料的陷阱参数的变化[24-26]。我们对环氧树脂的陷阱特性进行了分析。

图3(a)和3(b)为子模型P/G归一化表面电荷耗散曲线。图3(c)和图3(d)分别显示了子模型P的电子陷阱能量分布和子模型G的空穴陷阱能量分布。可以看出，子模型的表面电荷耗散速度随表面粗糙度的增大而增大，而后趋于平稳。从图3(c)可以看出，电子陷阱主要分布在0.90～0.97 eV之间。子模型P1、P2、P3的电子陷阱峰值密度低于子模型P0。从图3(d)可以看出，空穴陷阱主要分布在0.89～0.98 eV之间。子模型G1、G2、G3的空穴陷阱峰值密度低于子模型G0。

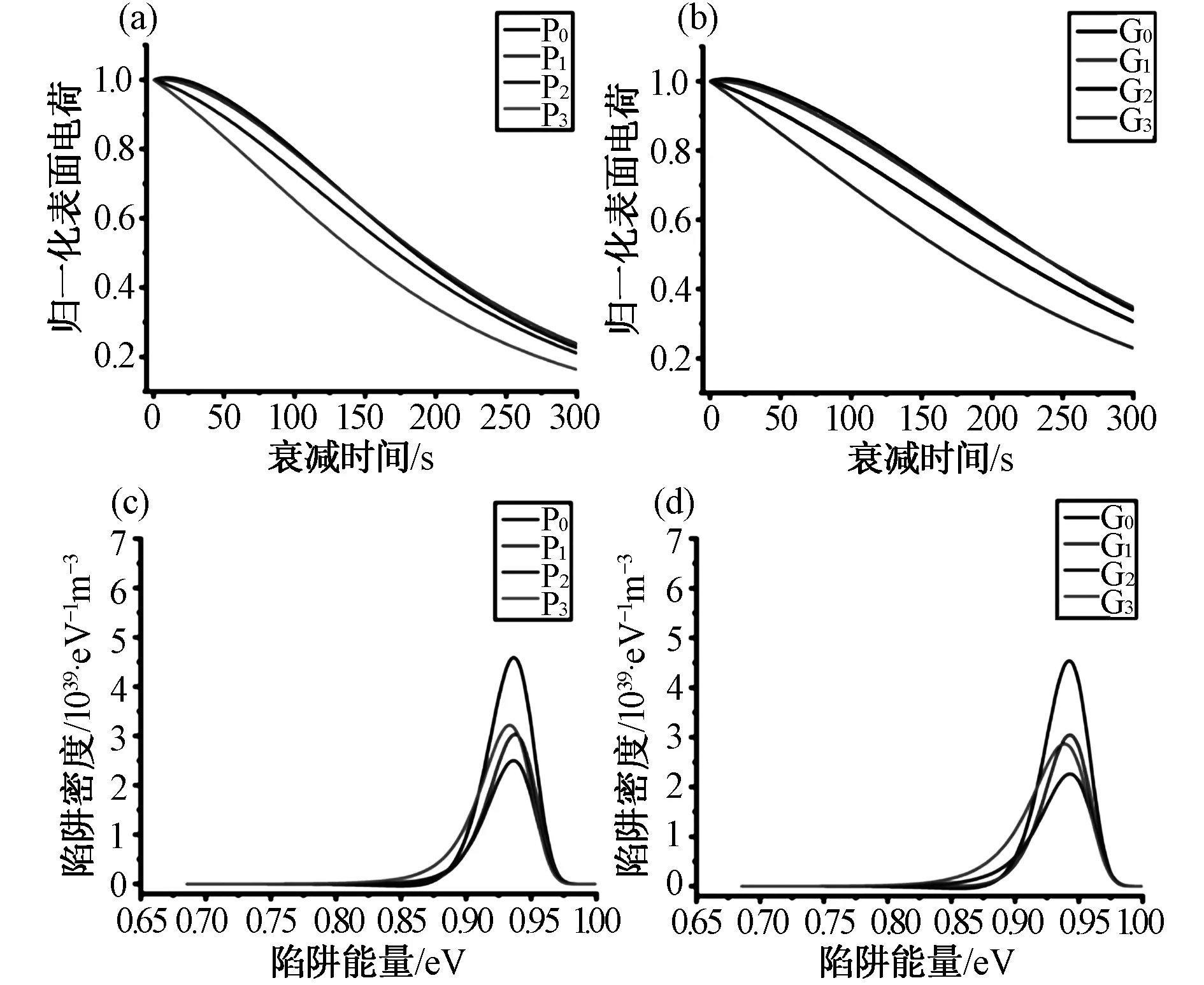
图3 (a)子模型P的表面电荷耗散曲线 (b)子模型G的表面电荷耗散曲线 (c)子模型P的电子陷阱能量 (d)子模型G的空穴陷阱能量Fig.3 (a) Surface charge dissipation curve of sub-model P (b) Surface charge dissipation curve of sub-model G (c) electron trap energy of sub-model P (d) positive hole trap energy of sub-model G

1.3 掺杂填料的子模型

当建立掺杂Al2O3纳米填料的模型时，认为暴露在表面的不同粒径的Al2O3纳米填料可以产生具有不同表面粗糙度的表面，采用随机生成的平均直径为25μm的球来表征子模型中环氧树脂中的Al2O3填料。设置Al2O3填料的相对介电常数为9，电导率为1×10-12S/m。Al2O3填料在环氧树脂内部的位置采用正态分布的随机数生成，体积分数为70%，严格贴近盆式绝缘子实际运行工况。四个子模型分别为P0/G0,P1/G1,P2/G2,和P3/G3。图4(a)为掺杂填料的子模型结构图，图4(b)为其电场分布。

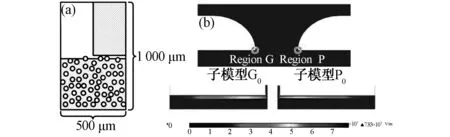
图4 掺杂填料的子模型结构图(a)和电场分布(b)Fig.4 Structure diagram (a) and electric field distribution (b) of sub-model of doped filler

表1给出了子模型P和G的平均电场幅值及其与主模型中相应区域的平均电场幅值的比值。由表1可以看出，比值接近于1，说明主模型和子模型具有相似的电场分布。即建立的子模型P/G的合理性。

表1 主模型和子模型的平均电场幅值Tab.1 Average electric field amplitude of main model and sub-model

图5为子模型P/G的表面电荷密度和最大电场幅值曲线。对于子模型P和G，电极附近的表面电荷密度和最大电场幅值均随表面粗糙度的增大而减小。

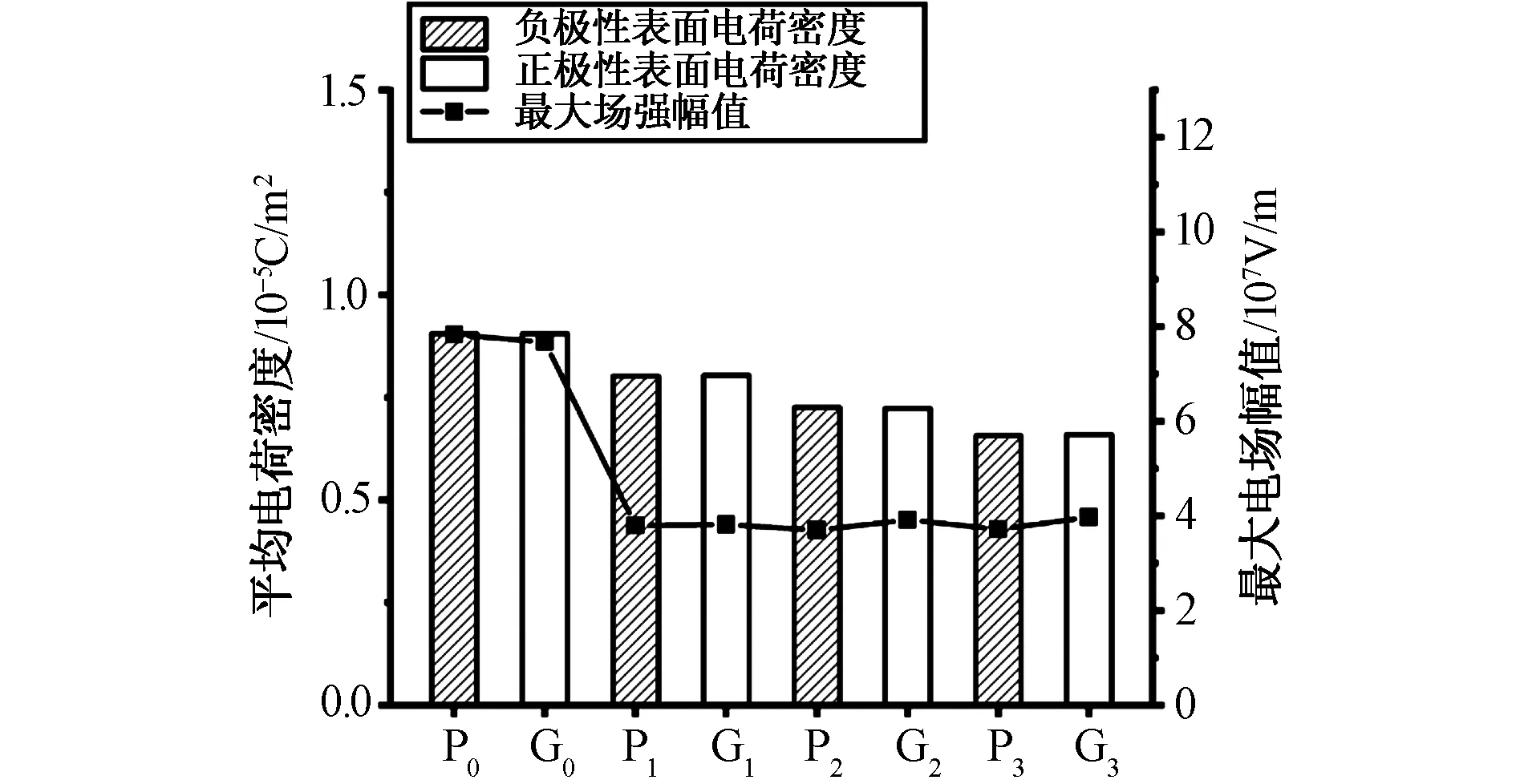
图5 子模型P/G的平均表面电荷密度和最大电场幅值Fig.5 Average surface charge density and maximum electric field amplitude of sub-model P/G

表2显示了子模型P/G峰值陷阱密度，可以看出，随着表面粗糙度的增大，峰值陷阱密度持续减小，子模型的表面电荷耗散率增大。

表2 子模型P/G的峰值陷阱密度Tab.2 Peak trap density of sub-model P/G

图6(a)和图6(b)为子模型P/G归一化表面电荷曲线。图6 (c)和图6 (d)为子模型P的电子陷阱能量分布和子模型G的空穴陷阱能量分布。子模型P的电子陷阱主要分布在0.89～0.97 eV之间，其中P0的峰值陷阱密度最大。对于子模型G，其空穴陷阱密度位于0.90～0.97 eV。子模型G0的空穴陷阱峰值密度最大。

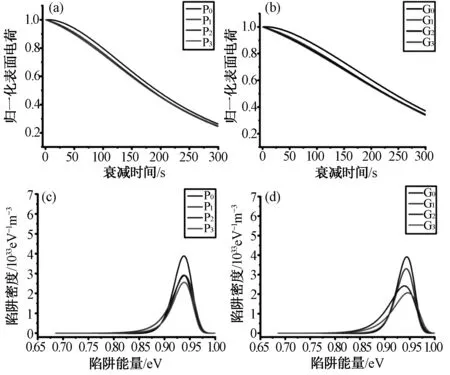
图6 (a)子模型P的归一化表面电荷曲线 (b)子模型G的归一化表面电荷曲线 (c)子模型P的电子陷阱能量分布 (d)子模型G的空穴陷阱能量分布Fig.6 (a) Normalized surface charge curve of sub-model P (b) Normalized surface charge curve of sub-model G (c) Electron trap energy distribution of sub-model P (d) Positive hole trap energy distribution of sub-model G

1.4 有无填料子模型的比较

模拟结果表明，当表面粗糙度增大时，无填料子模型和有填料子模型的表面电荷密度、最大电场幅值和峰值陷阱密度均呈大致减小的趋势。当环氧树脂表面粗糙度Ra在0.8～2.2μm范围内时，无填料子模型的表面电荷密度、最大电场幅值和表面电荷曲线变化显著。当表面粗糙度为1.3μm时，表面电荷密度和最大电场幅值最小。而在添加填料的子模型中，当环氧树脂表面粗糙度Ra在0.8～2.2μm范围内时，最大电场幅值和表面电荷曲线变化不明显。因此，环氧树脂表面粗糙度的变化和Al2O3填料的掺杂都会影响环氧树脂的表面电荷特性，且前者的影响要大于后者。

2 混合气体闪络试验

为了验证仿真的合理性，探索环氧树脂表面闪络特性与表面电荷特性之间的关系，在C4F7N/CO2混合气体中进行了闪络实验。

2.1 表面粗糙度控制

山东泰开集团环氧树脂的圆形样品厚度为5 mm，直径为50 mm。样品的体积电阻率为1×1015Ω·cm，介电常数为3.5。样品表面用电动磨床手工磨削；磨削方向为平行于电极磨削、垂直于电极磨削和无序磨削。采用TR130A表面粗糙度仪测量，取样长度为0.8 mm。从磨削表面取10个点测量Ra，保证误差不超过±0.05μm，表面粗糙度相对均匀。将样品的Ra控制在0.3μm、0.8μm、1.3μm和2.2μm。为防止测试点环氧树脂表面严重损坏，制备多个样品。图7为磨后样品的表面状态。

图7 磨削样品的表面状态(SEM扫描电镜，放大100倍)(a)Ra=0.3μm (b)顺序磨削Ra=0.8μm (c)顺序磨削Ra=1.3μm (d)顺序磨削Ra=2.2μm (e)未处理Ra=0.3μm (f)无序磨削Ra=0.8μm (g)无序磨削Ra=1.3μm (h)无序磨削Ra=2.2μmFig.7 Surface state of the grinding sample (SEM,magnified 100 times) (a)Ra=0.3μm (b) Sequential grinding Ra=0.8μm (C) Sequential grinding Ra=1.3μm (d) Sequential grinding Ra=2.2μm (e) Untreated Ra=0.3μm (f) Disordered grinding Ra=0.8μm (g) Disordered grinding Ra=1.3μm (h) Disordered grinding Ra=2.2μm

图8(a)为直流闪络实验平台，直流电压发生器(FVG±150 kV)通过保护电阻与高压电极连接。实验电极由直径为10 mm的不锈钢制成;两个电极之间的距离为10 mm。在密封的玻璃室中，将上表面紧贴电极的样品置于聚四氟乙烯平台上。闪络实验采用的气体环境为C4F7N/CO2混合气体(C4F7N/CO2比例为1∶4)，压力为0.1 MPa。

图8 直流闪络实验接线图(a)和俯视图(b)Fig.8 Wiring diagram of DC flashover experiment (a) and planform (b)

实验前，用无水乙醇擦拭电极和环氧树脂样品表面，样品自然干燥后固定在手指型电极之间，以保证表面清洁无电荷残留。将电极置于试验腔体内，用真空泵将试验腔体内的气体抽出。将混合比为1∶4的C4F7N/CO2混合气体处理至压力为0.1 MPa。待试样完全静止后，以平均1 kV/s的速度逐步升高电压，直至试样表面发生闪络。记录闪络电压值，并测量10个有效数据，然后更换气体和样品，并重复上述步骤。

2.2 表面粗糙度对表面闪络的影响

图9 (a)和(b)为三种磨削方式后样品表面正、负闪络电压对比图。可以看出，无序磨削后样品的闪络电压增强效果要优于有序磨削样品。

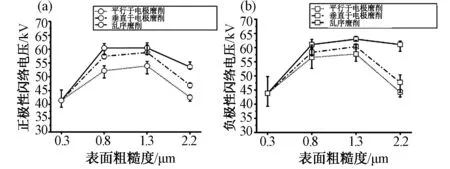
图9 不同极性闪络电压随Ra的变化曲线 (a)三种电极磨削方式下的正表面闪络电压 (b) 三种电极磨削方式下的负表面闪络电压Fig.9 Flashover voltage curve with Ra under different polarities (a) Positive surface flashover voltage under three electrode grinding modes (b) Negative surface flashover voltage under three electrode grinding modes

对于Ra=0.8μm的样品，无序磨削后样品表面正闪络电压比平行磨削和垂直磨削后样品分别提高了8.01%、4.75%。当Ra=1.3μm时，无序磨削后样品表面正闪络电压分别提高了9.09%、4.41%;当Ra=2.2μm时，无序磨削后样品表面正闪络电压分别提高了38.04%、27.92%。

对于Ra=0.8μm的样品，无序磨削后样品的负表面闪络电压比平行于电极和垂直于电极磨削的样品分别提高了15.75%、5.21%。对于Ra=1.3μm的样品，无序磨削后试样表面负闪络电压分别提高了12.05%、2.82%。对于Ra=2.2μm的样品，无序磨削后试样表面负闪络电压分别提高了25.82%和14.00%。

表3为环氧树脂样品表面闪络电压的Weibull分布参数β。图10(a)～(c)为环氧树脂样品表面闪络的Weibull分布。

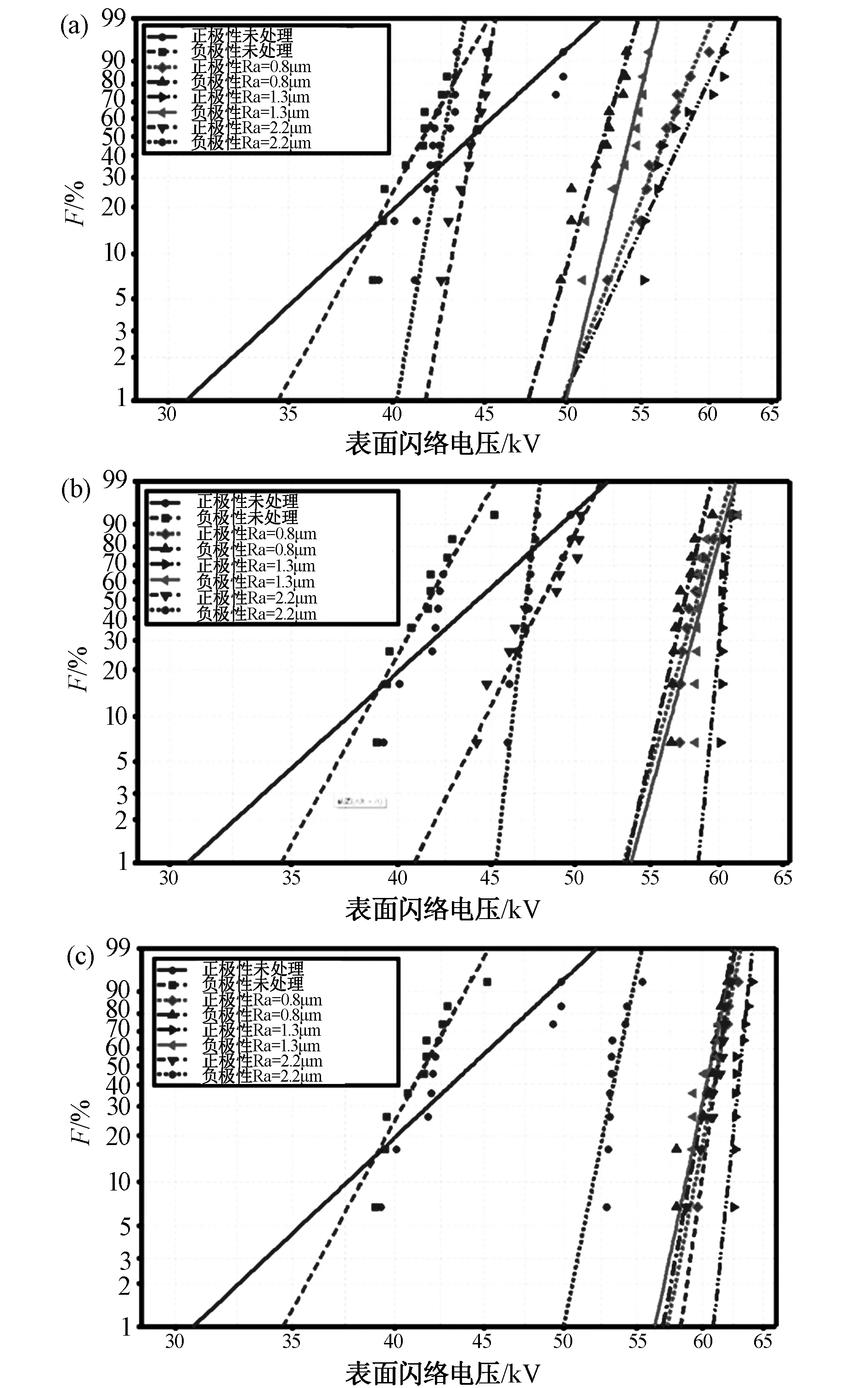
图10 表面闪络电压的Weibull分布 (a)平行于电极磨削 (b)垂直于电极磨削 (c)无序磨削Fig.10 Weibull distribution of surface flashover voltage (a) Grinding parallel to the electrode (b) grinding perpendicular to the electrode (c) disordered grinding

表3 环氧树脂样品表面闪络电压的Weibull分布参数βTab.3 Weibull distribution parameters β of flashover voltage on epoxy resin surface

双参数Weibull分布密度函数如下：

(1)

尺度参数α代表失效概率为0.63(1-1/e)时的闪络电压，形状参数β代表拟合曲线的斜率。β值越大，闪络电压分散性越小。通过对实验测试结果的Weibull分布拟合，可以评价环氧树脂样品的闪络电压离散度。可以看出，在C4F7N/CO2混合气体中，对样品进行粗糙度处理的表面闪络电压的形状参数β增大，即粗糙度处理会降低表面闪络电压的分散程度。

2.3 分析

粗糙度对环氧树脂表面闪络电压的影响表现为沿面闪络电压随表面粗糙度的增大先提高后降低。结合仿真和实验，这种效应主要通过表面电场和表面电荷运动的影响来实现的。

由于在闪络的过程中正电荷和负电荷的运动是相对的，所以本文以电子为例说明闪络过程中的表面电荷运动机理。当表面粗糙度较小时，提高样品表面粗糙度相当于增加环氧树脂表面沟槽的数量和深度，这使得电荷在电场的作用下增加了爬电距离，在运动过程中有更大的概率被环氧树脂表面的陷阱捕获。能够产生电子崩的种子电子的数量大大减少。且二次电子发射有一定的概率被沟槽阻挡，从而阻止了表面闪络，此时环氧树脂的沿面闪络电压提高。但是当环氧树脂表面粗糙度过大时，相当数目的电子可能进入环氧树脂样片表面的凹槽中，无法运动出来，当凹槽半径大于电子碰撞电离所需的自由行程，反而会促进电子崩的形成。因而对于粗糙度过大的情况，沿面闪络电压反而存在降低的可能。

表面电荷积聚与表面粗糙度有关。本文认为，一方面，表面粗糙度处理引起的材料表面的波动相当于表层气隙增大，改变了局部电导率，注入气体间隙的电流增加，陷阱电荷减少，相当于降低了环氧树脂的陷阱密度；同时，表面积的增加增大了脱困电荷与气体中载流子相遇的概率，因此粗糙度越大表面电荷越不易集聚，即环氧树脂表面电荷消散速率随表面粗糙度的增大而增大。

与有序磨削相比，无序磨削后的样品使环氧树脂样品表面形貌复杂化，因此环氧树脂表面凹槽分布的随机性和分散性更大。粗糙表面增大了电荷沿电场方向的移动和放电路径，阻碍了电子雪崩的形成，所以闪络电压上升得更多。

3 结 论

本文建立了表面电荷模拟模型，探讨了粗糙度对环氧树脂表面电荷特性的影响。此外，还进行了闪络实验，探讨了环氧树脂表面闪络特性与表面电荷特性的关系。主要结论如下：

(1)环氧树脂表面粗糙度的变化比掺杂Al2O3填料对表面电荷特性的影响更大。

(2)在C4F7N/CO2混合气体中，样品的表面闪络电压随表面粗糙度的变化先增大后减小。

(3)表面粗糙度处理通过改变表面电荷特性和局部电场来影响绝缘材料的表面闪络特性，合理调控表面粗糙度可以提高环氧树脂的绝缘性能。