结合卷积神经网络和迁移学习的电机轴承故障诊断方法

李俊卿，刘 静

(华北电力大学 电气与电子工程学院，保定 071003)

0 引 言

轴承是电机设备中十分重要的基础元件，但同时也是最易损的部件之一。由轴承故障诊断的现有研究来看，基于振动信号的诊断方法是国内外最为普及且较为有效的检测方法[1-3]。传统的诊断步骤主要是通过传感器采集大量振动信号后，利用信号处理手段分析故障特征从而实现故障诊断。

针对轴承故障信号处理的传统方法有时域法、频域法以及时频分析法[4]。其中，时频法能从时域和频域两个维度获取信息，可以反映信号的局部特征，从而提取更准确的特征。小波分析是时频法的代表方法之一，其利用有限长的会衰减的小波基达到了同时获取频率与时间特征的效果，得到了广泛应用。然而，对时频图的人工特征提取需要大量的经验和专业知识。随着智能化时代的到来，仅仅依赖于传统特征提取的方法不再适用，其效率低、工作量大、受限于先验知识和专家经验的问题逐渐凸显。

2006年，深度学习的先驱者Hinton在《Science》的发表了一篇轰动一时的论文，打破了神经网络发展的瓶颈[5]，各行各业都掀起深度学习的浪潮。作为属于人工智能领域下机器学习里的分支[6]，深度学习具有特征工程完全自动化的优势，克服了传统的机器学习技术存在的需要进行人工选择特征的问题，极大地简化了工作流程。

深度学习的兴起开拓出故障诊断的一个新领域，近年来在故障诊断领域的应用逐渐广泛。文献[7]提出了一种结合卷积神经网络(Convolutional Neural Network，CNN)和峭度的故障诊断方法，将振动信号分段处理得到峭度指标，将峭度指标转换为灰度图，送入卷积神经网络完成故障分类。文献[8]将一维振动信号以400个数据点为样本长度进行截取，按分段组合的方式构建二维矩阵，并将得到的数据矩阵直接输入卷积神经网络。文献[9,10]采用相似的分段组合的方式将原始的一维时域信号转换为二维的灰度图，使用二维卷积神经网络进行特征提取。文献[11]通过分段组合的方式将原始监测信号映射到二维矩阵中，经卷积神经网络自动学习高维特征实现轴承的故障诊断。文献[12]建立了基于一维卷积神经网络的自适应故障诊断模型，以原始振动数据直接作为输入实现故障分类。文献[13]提出了一种长短期记忆网络(Long short-term memory，LSTM)与Softmax多分类器结合的诊断方法，将采集的振动信号进行归一化后，利用长短期记忆网络处理数据提取特征。

可以看出，现有方法的思路大多是将采集到的信号进行分段截取，通过分段组合的方法构建为二维数据矩阵，或是将一维的振动信号直接输入长短时记忆网络或一维卷积神经网络进行训练，此类方法的缺点是不能充分提取样本中的特征。此外，现阶段针对电机轴承故障诊断的研究大多基于同一工况下的数据，提出的方法仅在固定的工况下有较高的准确率。由于实际工程应用中设备的工况多变，要获取每个工况下大量带标签的数据比较困难，有效数据的缺乏导致方法的泛化性和实用性不高，成了基于深度学习的故障诊断技术的发展和应用的瓶颈之一。因此，研究一种新的方法能充分提取有限样本中的特征，并解决变工况下有效样本不足导致故障诊断效果不佳的问题是必要的。

迁移学习也是机器学习的一个分支，能将学习到的知识迁移到不同但相关的学习任务，在文本、情感和图像分类上应用广泛[14]。由于深度学习模型本质上具有高度的可复用性，其与迁移学习相结合的方法可以利用现有的数据帮助实现新领域的分类。因此，针对以上问题，本文提出了一种结合卷积神经网络和迁移学习的电机轴承故障诊断方法，利用卷积神经网络强大的图像处理能力，对振动信号小波变换后的彩色时频图进行特征提取，并引入迁移学习提升模型在其他工况下的泛化性。

1 故障诊断方法

1.1 小波变换

小波变换是时频法的代表方法之一，其利用的小波基有限长且会衰减，可以同时获取频率与时间的信息。相较于傅里叶变换具有了更高的分辨率[15]。相比于同样是时频法的短时傅里叶变换，小波变换能更好地平衡时间分辨率和频率分辨率的表现。相比于离散小波变换，连续小波变换生成小波系数能直观表达信号的全局特征，从而更好的提出信号的特征值，有利于相似信号的辨别和分析。

对函数f(t)∈L2(R)，其连续小波变换的表达式为

(1)

式中：a表示尺度因子；τ表示平移因子，而Ψa,τ(t)为小波基函数。由于连续小波变换在选取小波基时，其函数波形应与分析对象的特征相似，本文选取cmor小波基。

1.2 卷积神经网络

卷积神经网络是一种应用广泛的深度学习模型，具有强大的图像处理能力。CNN由若干卷积层(Convolutional layer)、池化层(Pooling layer)、全连接层(Fully connected layer)组成，如图1所示。由于卷积层学到的是局部模式，且具有平移不变性，因此对于感知任务可以高效地利用数据。此外，CNN的多层次结构可以从大量数据中提取深层次关系，避免了人工特征提取的操作，即实现了特征工程自动化[16]。

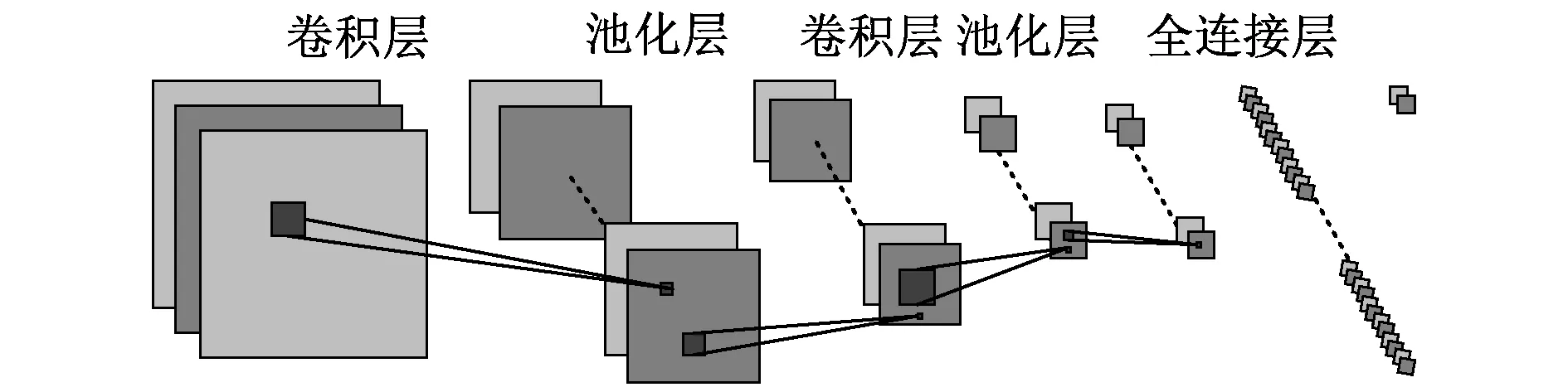
图1 CNN模型示意图Fig.1 Schematic diagram of CNN model

在卷积神经网络的应用中，过拟合往往是核心难题，其原因是训练样本较少，导致模型在有限的训练数据上过于优化，最终学到的只适用于训练数据，而在从未训练过的数据上表现很差。针对此问题，可以从数据样本和网络结构两方面入手改进卷积神经网络。本文利用数据增强和Dropout机制进行了网络的优化，抑制了过拟合从而提升模型泛化性。

数据增强在计算机视觉领域是一种强大的降低过拟合的技术。其方法通过旋转、剪裁和平移等方式，在不改变特征空间结构的前提下，从现有的样本数据中生成更多的有效样本。由于数据是一切机器学习问题的基础，任何深度学习模型都需要在大量且有效的数据上进行训练，进而获取准确分类或拟合的能力。数据越多，训练出的模型效果越好。因此，在实际工程应用中遇到样本不足导致诊断精度不高的问题时，数据增强能显著提升有效样本的个数，抑制模型过拟合。本文在训练网络过程中，通过对图像随机进行轻微程度的小角度旋转、小范围剪裁和平移，从而生成更多可训练的可信图像样本，因此，增加了网络训练样本的数量，使得训练好的模型能学习到更多内容。

此外，Dropout机制也是防止神经网络过拟合的有效方法之一，对网络中的某一层使用Dropout机制就是在训练中随机地将一些特征设置为0，通过随机地舍弃特征减少每次训练的神经元数量，相当于在每一层的输出里加入噪声，增强了泛化能力。

1.3 迁移学习

迁移学习也是机器学习领域的一个分支，分为样本迁移、特征迁移、模型迁移、关系迁移等方法。通常来讲，基于海量数据提取特征的深度学习方法都是通过历史数据进行训练，然后使用同一学习任务下的数据在训练好的网络里进行预测或拟合。与之不同的是，迁移学习能从源域中的现有样本中得到训练，当有新的应用场景出现时，能利用源域中学习到的知识实现目标域的分类，此时源域和目标域的数据不必严格满足独立同分布的假设[17]。

本文采取的是模型迁移，将训练过程分为两个步骤。首先用样本充足的某一工况下的数据集训练网络，确定网络的结构和参数并进行优化，使网络学习到可通用的泛化特征。通常，网络结构里越靠底部的层所学习到的特征会越通用，顶层结构则会学习到更加抽象以及专业化的特征表示。因此，需要应用到不同工况的小样本数据集时，将训练好的底层卷积层和池化层的参数权重冻结，仅将全连接层和顶层卷积基的参数设置为可训练的。通过冻结顶层结构并设置一个学习率非常小的优化器，用不同工况的小样本数据再次训练，对顶层结构的参数进行微调，使得网络大部分参数不变，仅让顶层学习到针对不同工况下更专业的特征。

1.4 提出方法的步骤

本文提出的诊断方法的步骤如下：

(1)小波变换得到时频图：对原始信号批量进行小波变换，得到有利于进行CNN训练的图像；

(2)数据集划分：将所有得到的样本划分为训练集、验证集和测试集。其中，训练集用于让模型学习知识，验证集用于确定模型的最优参数，测试集用于评估模型的最终效果；

(3)用时频图训练CNN：对时频图进行预处理，构建卷积神经网络进行训练，根据训练结果确定参数，通过数据增强和Dropout机制增加有效样本并抑制过拟合，从而优化网络；

(4)引入迁移学习提升泛化性：冻结网络的底层结构，用不同工况的小样本数据对网络的顶层结构进行微调。

2 实例分析

2.1 小波变换构建数据集

本文的数据选自来自美国凯斯西储大学(Case Western Reserve University)的滚动轴承试验台，该试验台主要由电机、轴承和负载电机组成。其故障方式为人为钻孔或切割，用加速度传感器采样振动信号，采样频率为12kHz和48kHz。该数据集共包括了正常状态、内圈故障、滚子故障和外圈故障四种类型的样本。本文选取12kHz采样频率下，转速为1797r/min、1772r/min、1750r/min以及1730r/min时的驱动端振动数据，分别对应0HP、1HP、2HP、3HP四种不同的工况。图2为1797r/min转速下采集到的原始加速度振动信号(前2 000个数据点)。

图2 振动信号时域图Fig.2 Time domain diagram of vibration signal

构建数据集A、B、C和D，如表1所示，数据集A选取0HP工况下的振动数据，用以训练模型，数据集B、C和D分别选取1HP、2HP和3HP工况下的数据，用以验证模型在其他工况的小样本下的泛化性和迁移效果。将采集到的数据进行分割，在数据集A中，每种状态只保留前115200个数据点，以1280个数据点为一个样本，包含大约转动三圈的数据，形成90个样本。依据此规则建立4种轴承运行状态的数据集，包括不同的故障类型和故障程度(故障直径分别为7in，14in，21in)。为了更好地训练和评估模型，将正常状态下的90个样本分为60个样本的训练集、20个样本的验证集以及10个样本的测试集。同理，将三种故障(内圈故障、滚子故障和外圈故障)的各270个样本分为180个训练样本、60个验证样本以及30个测试样本。其中，训练样本由三种故障程度(7in，14in，21in)各60个样本组成，验证样本由三种故障程度各20个样本组成，测试样本由三种故障程度各10个样本组成。经过构建，数据集A共有600个训练样本、200个验证样本以及100个测试样本，每个样本包含1 280个数据点。以相似的方式构建另外三个数据集，各包含200个训练样本、100个验证样本以及100个测试样本。

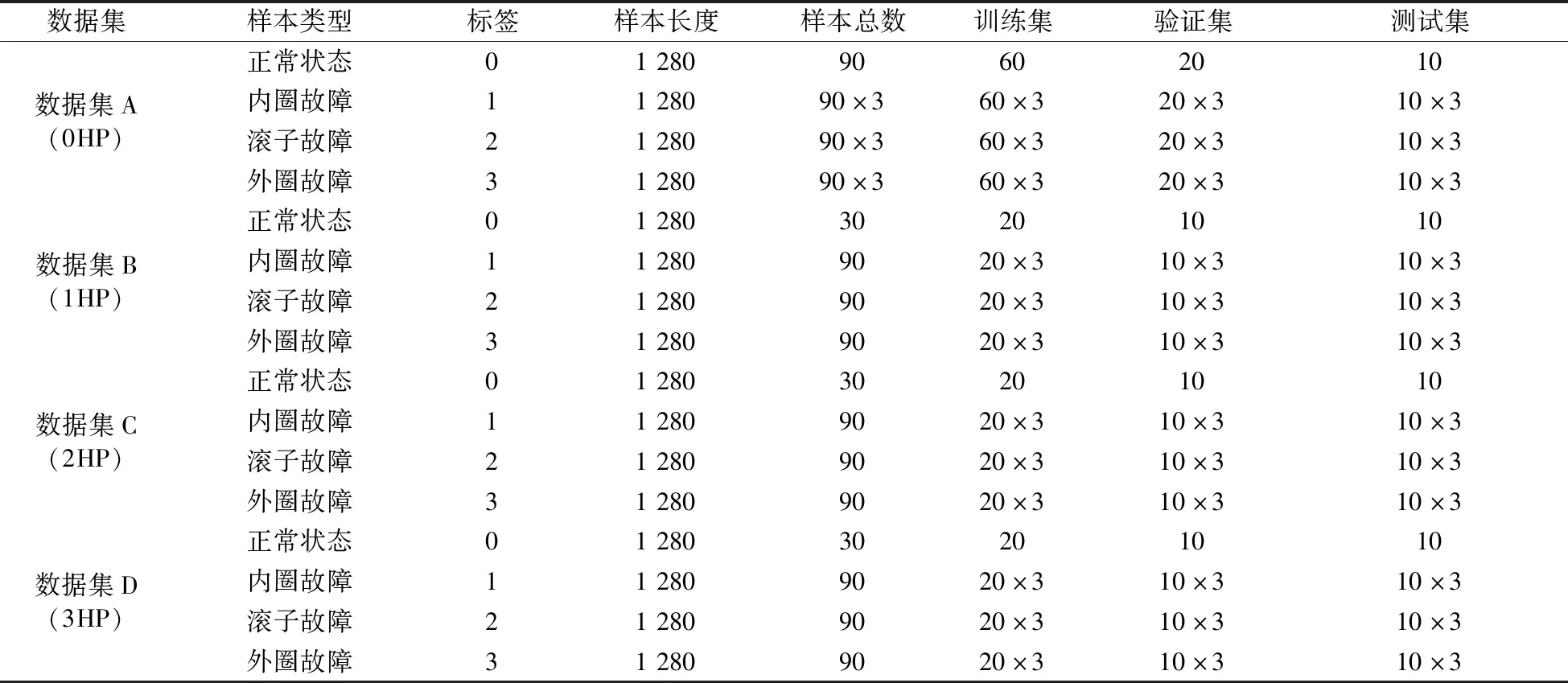
表1 实验数据集Tab.1 Experimental datasets

结合振动信号的时域图，选用自适应性能良好的 cmor小波基，对4种状态下每个样本的振动信号分别进行小波变换，得到用于CNN训练的时频图(800×800像素)，如图3所示。

图3 小波变换时频图Fig.3 Wavelet transform time-frequency diagram

2.2 卷积神经网络构建与训练

在实验过程中，使用数据集A的样本按批量样本的输入方式进行卷积神经网络的训练，用该数据集的验证样本确定模型的最优参数。在网络构建过程中，按照前文所述的理论在网络的密集连接分类器前加入了Dropout层，并在训练中使用了数据增强技术以抑制过拟合。所有样本的训练和测试过程都是基于python语言在pycharm平台上实现的，其中，本文选取的深度学习前端框架是基于Tensorflow的Keras，本文的数据增强的过程是在Kera中通过类ImageDataGenerator实现的，通过随机旋转、移动、剪切图像生成更多可信样本，可以起到抑制过拟合的作用，进而增强模型泛化性。本文模型需要通过实验确定的网络参数有优化器类型、卷积层数、批量样本大小，按照单一变量法的原则改变参数进行实验。

(1)优化器的选择

优化器的作用在于决定如何基于损失函数对网络进行更新，即确定梯度下降的具体方法。本文备选的优化器有 SGD、Adam 和RMSprop，均采用其默认的学习率用于模型训练。当采用不同优化器时，训练精度随着训练批次的变化趋势如图4所示。纵坐标为训练精度，横坐标为训练批次，即所有训练数据的迭代次数。可以看到，相较于SGD和RMSprop优化器，Adam的训练精度的最终值较高，且在迭代次数较小时便达到了稳定，因此选择Adam优化器。

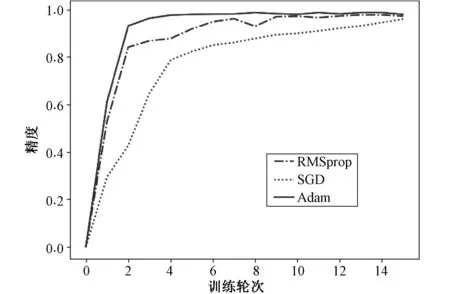
图4 不同优化器的对比Fig.4 Comparison of different optimizers

(2)网络层的选择

在卷积神经网络中，卷积层的作用是从数据中提取特征，池化层的作用是减少需要处理的特征图的元素个数，并让最后一个卷积层包含全部的输入信息。网络层数的选择对构建网络来说至关重要，如果网络层数过少，那么较小的网络容量容易出现信息瓶颈，不能处理复杂问题，如果网络层数太大，会使得其结构比较复杂，对比较简单的分类问题来说容易出现过拟合。如表2所示，采用以下五种方案，分别包含不同的卷积层和池化层，对数据集进行训练，在验证集上的精度如表2所示。从实验结果可以看出，方案2的精度更高，即应选择3个卷积层和4个池化层的网络结构。

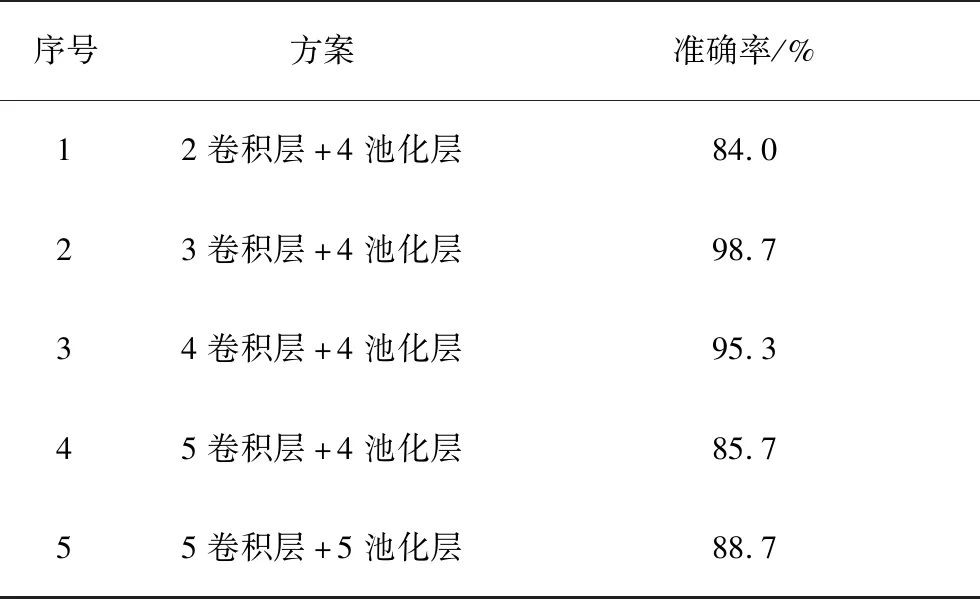
表2 不同网络结构的对比Tab.2 Comparison of different network structures

(3)批处理样本数的选择

网络在训练的过程中，目标是找到一组模型参数，使得在给定的训练样本和对应目标值上的损失最小。为了不使模型陷入局部最优，减小损失是通过小批量迭代来实现的，即将训练样本分成多个批次进行迭代训练。选择不同的批处理样本数，以每轮的平均训练时间和验证集准确率作为评价指标，实验结果如表3所示。可以看到，批处理样本为5或者10时，准确率差别不大，但相较于批处理样本数为5而言，批处理样本数为10时训练时间明显较少，训练速度更快，因此确定批处理样本数目为10。

表3 不同批样本数的对比Tab.3 Comparison of different batch-sizes

综合以上实验结果，本文确定网络使用Adam优化器，批处理样本数目为10，网络结构如下表4所示。该CNN网络输入特征图的大小为150×150，含三个卷积层和四个最大池化层，一个Dropout层，两个全连接层，共有429万个参数需要训练。三层卷积与四层池化的组合增大了网络容量，也减小了特征图的尺寸，使得网络具备处理复杂图像的能力，且计算代价不会太大。由于本文的故障诊断本质上是一个四分类问题，所以网络的最后一层用的softmax分类器实现状态分类，并用分类交叉熵作为损失函数。

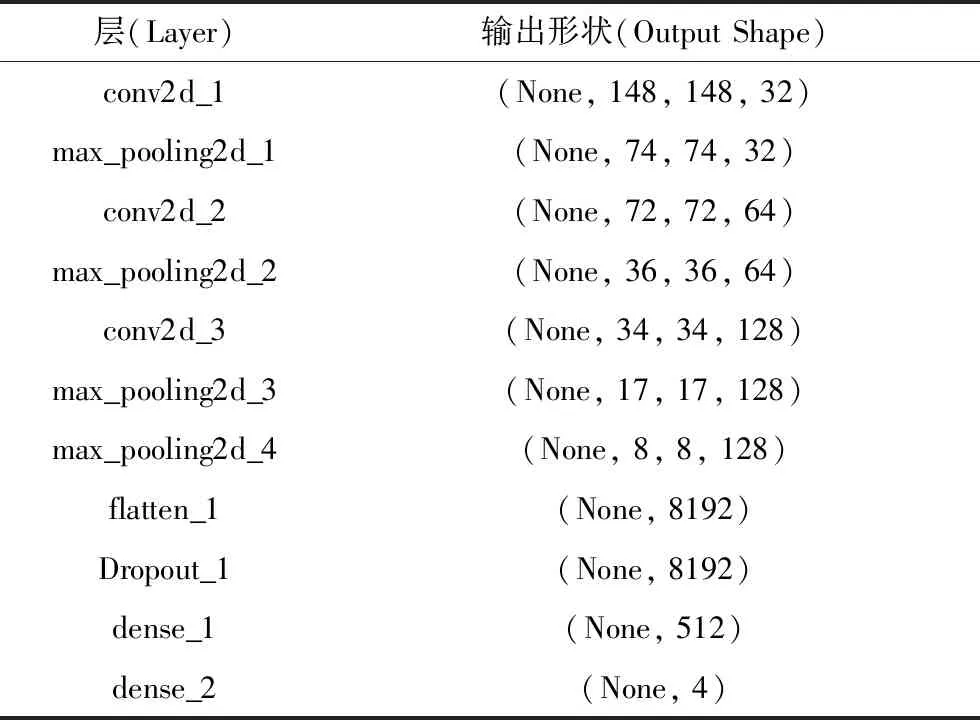
表4 网络结构Tab.4 Network structure

经小波变换后，数据以JPEG文件的形式保存。将保存的图像解码为RGB三维矩阵数据，再将像素值(0～255)缩放到[0,1]区间。用经过预处理后的数据对使用了数据增强的网络进行训练，分别绘制网络在训练集和验证集上的损失和精度，如图5和图6所示。从图像中可以看到，训练精度和验证精度随着时间增加，到第九轮时接近100%，分类效果非常好，训练损失和验证损失也在第九轮时接近至0，后面不再变化。

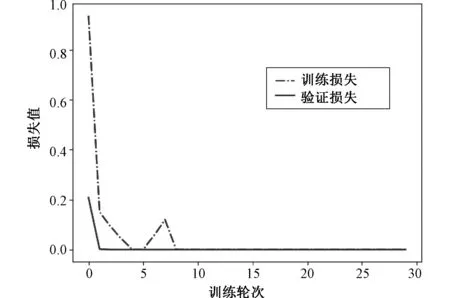
图5 训练损失和验证损失Fig.5 Training and validation loss

图6 训练精度和验证精度Fig.6 Training and validation accuracy

2.3 迁移学习

前文的训练都是基于有充足数据的数据集A，但在实际工程应用中，往往会出现变工况下有效样本不足的问题，为了对未训练工况下的小样本实现高精度的故障诊断，引入迁移学习的方法。将数据集A作为源域数据集，其他三个数据集作为目标域数据集。模型在数据集A上训练完成后，冻结网络的底层结构，用数据集B、C和D的各200个训练样本对网络的顶层结构进行微调，再分别在数据集B、C和D的各100个测试样本上评估分类效果。微调的具体过程是在对200个样本进行训练时通过设置学习率非常小(为1×10-5)的优化器来实现的，在底层结构冻结的前提下，极小的学习率使得顶层结构参数的变化范围很小，即这次训练仅会微调全连接层以及顶层卷积基的参数，不会破坏之前学习到的更加通用的特征。实验结果如表5所示，可以看到，在有充足训练样本的数据集A上，准确率达到了99.8%。数据集B、C和D的训练样本虽然只有数据集A的三分之一，但在引入迁移学习后，准确率也能高达95%以上。可见结合卷积神经网络和迁移学习的方法在其他工况样本不足的情况下是有效的，能极大提升泛化性。

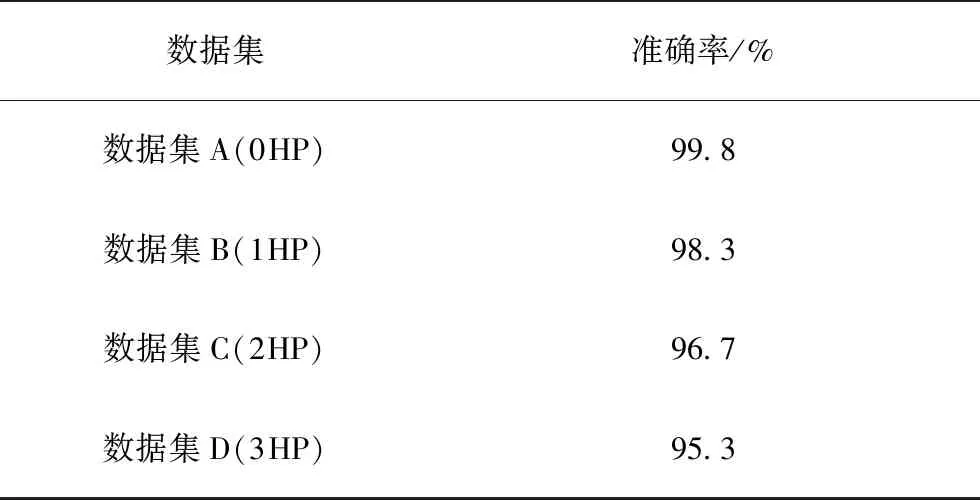
表5 不同数据集的准确率Tab.5 Accuracy of different datasets

2.4 对比分析

为了说明提出方法的优势，对比分析了提出方法与以下方法的测试结果。方法一采用卷积神经网络，不进行小波变换和迁移学习，按横向插样的方式构建二维数据矩阵，构建和本文数量相同的样本，并将数据矩阵直接作为卷积神经网络的输入。方法二结合了小波变换和卷积神经网络，但不进行迁移学习。方法三为本文方法，结合了小波变换和卷积神经网络，并引入了迁移学习。

将以上三种方法分别在数据集A、B、C和D上进行训练，为了避免实验结果的偶然性，对三种方法分别进行10次实验，取准确率的平均值作为该方法的最终精度，实验结果如表6所示。

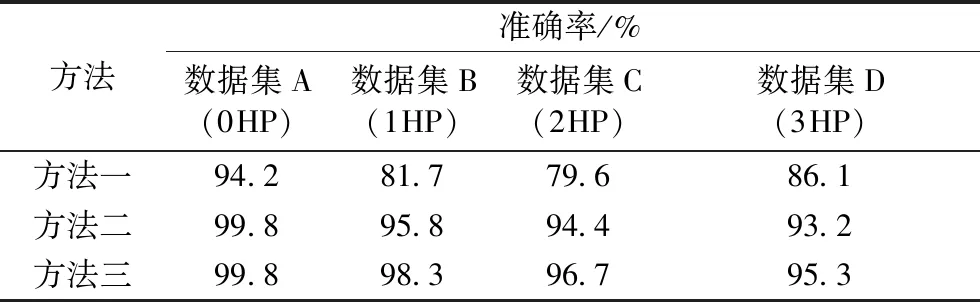
表6 三种方法对比Tab.6 Comparision of three methods

分析实验结果可得以下结论。三种方法均在数据集A上的准确率最高，在数据集B、C和D上较低，说明当训练样本充足时，能获得更好的分类效果，当训练样本不足时，分类精度将相应降低。对比三种方法，方法一的准确率明显不如方法二，说明相比于直接将原始信号以数据形式输入，提出方法结合了小波变换，使得卷积神经网络能更好地从时频图里能提取特征。此外，方法三在数据集B、C和D上的准确率优于方法二，说明提出方法在同是小样本的情况下，通过引入了迁移学习实现了更高的精度。因此，实验结果证明，小波变换与卷积神经网络结合的方法能充分提取数据特征并高效利用样本，而迁移学习方法的引入使得在变工况时，能利用极少的样本和训练时间实现较高的分类精度。

由于数据集为不平衡样本，为了进一步说明提出方法分类的准确性，对本文方法对数据集B的分类结果绘制混淆矩阵，如图7所示。其中，横坐标的标签表示模型所预测的运行状态，纵坐标表示实际的运行状态，右侧条形图的颜色越深，表明越多的样本被正确分类。由图可得，100个样本中，正常状态下的10个样本全部诊断正确，外圈故障的30个样本和滚子故障的30个样本也全部正确分类，仅有内圈故障的两个样本被错误诊断为外圈故障，整体准确率为98%，说明分类效果良好，诊断精度较高。

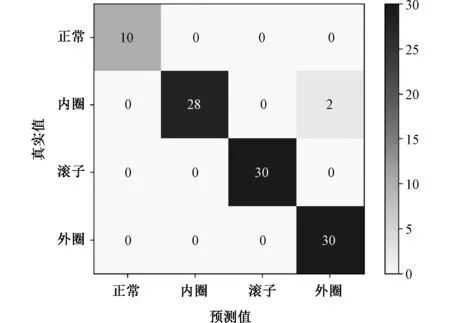
图7 混淆矩阵Fig.7 Confusion matrix

3 结 论

本文提出了一种基于卷积神经网络和迁移学习的电机轴承故障诊断方法，在实际的复杂工况中样本不足，构建可靠分类模型比较困难时，提出方法能利用极少的样本实现不同工况下的准确故障诊断。提出方法对振动信号小波变换得到有利于卷积神经网络训练的彩色时频图；通过训练确定网络的结构和参数，利用数据增强技术和Dropout机制优化网络；采用模型迁移的方式，对不同工况下的小样本实现了准确识别；并通过对比分析验证了提出方法的有效性。主要创新点如下：

(1)提出方法结合了小波变换和卷积神经网络，利用小波变换获取时域频域两个维度的信息，凭借多层次结构的卷积神经网络强大的图像处理能力实现特征工程自动化，从大量数据中提取深层次关系，充分利用了样本里的信息；

(2)针对卷积神经网络的过拟合问题，提出方法利用数据增强技术和Dropout机制进行了网络结构和数据的优化，增加了有效样本，抑制了过拟合；

(3)提出方法引入了迁移学习，与需要大量带标签数据的传统方法相比，能在变工况下的小样本数据上实现较高的准确率，提升了模型的泛化能力，具有明显优势。