浅析物理竞赛对迈克尔逊干涉仪原理和实验的考查
何文明
(河北邯郸市第一中学,河北 邯郸 056002)
2021年第38届全国中学生物理竞赛有两道关于迈克尔逊干涉仪的试题,其一是复赛(扬州福建赛区)理论题,其二是决赛的实验题.同一年份在同一内容处编写两道大题的情况并不多见,这提醒教练和考生,物理学发展过程中起到关键作用的新理论、新仪器的学习和应用,应当引起足够的重视.
迈克尔逊干涉仪是1883年美国物理学家迈克尔逊和莫雷合作,为研究“以太”漂移而设计制造出来的精密光学仪器.它是利用分振幅法得到双光束来实现的干涉.在近代物理(如引力波的测量)和近代计量技术(如标定标准米单位、光谱精细结构)中迈克尔逊干涉仪有着精彩的表现.迈克尔逊本人也因此荣获1907年度诺贝尔物理学奖.
1 迈克尔逊干涉仪的工作原理
如图1是迈克尔逊干涉仪的结构,包括光源S、分束板G1、补偿板G2、反射镜 M1(固定)和 M2(可调)、观察屏P.分束板后表面镀有一层半透半反膜,当光波入射到分束板上时,被分为两束光1和2,光束1经平面镜M1反射,光束2经平面镜M2反射,最后两束反射光在观察屏P处相遇发生干涉.注意图中的M2′不是干涉仪中的一个元件,而是M2相对分束板G1镀膜的镜像,正因为这样,光束1、2也可看成经M1和M2′之间形成的空气薄膜反射后发生干涉.

图1
(1)等倾干涉.
当M1和M2′平行时,所观察到的是等倾干涉条纹,如果光线在空气薄膜中的折射角用θ表示,则明纹中心(注意:不是圆环中心)满足光程差δ=2nd cosθk=kλ;暗纹中心满足光程差δ=2nd cosθk=(2k+1)λ/2.
等倾干涉条纹的特点:① 条纹为一系列同心圆;② 条纹内疏外密,级次内高外低;③ 圆环中心处不一定是明条纹或暗条纹中心,即光束1、2光程差不一定是光波长的整数倍或半整数倍;④ 当d变大时,圆形干涉条纹更高级次的环从中心冒出,所有的环都向外扩;反之,当d减小时,原更高级次的环从中心缩进,所有的环都向中心收缩.随着M1和M2′的间距d改变,观察屏上的条纹变化情况为如图2所示.
(2)等厚干涉.
当M1和M2′不平行时,形成劈尖,干涉条纹为等厚干涉条纹.这里有一个问题应当注意,就是用白光实验时,由于白光的光谱范围大,相干长度很小,等厚条纹主要出现在M1和M2′的交棱位置附近,所以实验时寻找等光程交棱位置必不可少.但不能用单色光寻找交棱位置,因为用单色光实验时总有几条暗线位置,无法确定哪条暗线对应等光程交棱位置,而且用单色光实验不必使用补偿板G2.使用白光来精确定位交棱这个等光程位置,必有补偿板G2,因为只有加上它,等光程交棱位置成为唯一的暗条纹位置.等厚干涉随间距变化如图3所示.
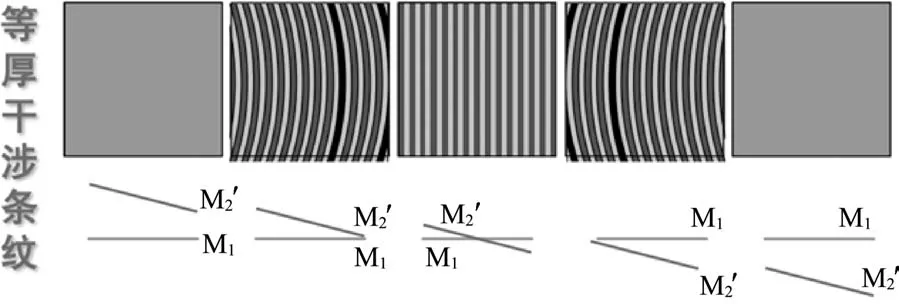
图3
2 竞赛真题赏析
题1.(第38届中学生物理竞赛复赛扬州福建赛区第七题)迈克尔逊干涉仪的光路原理图如图4所示.在焦距为f的透镜L的焦平面上放置观察屏,观察到的干涉图样是一系列同心圆环.
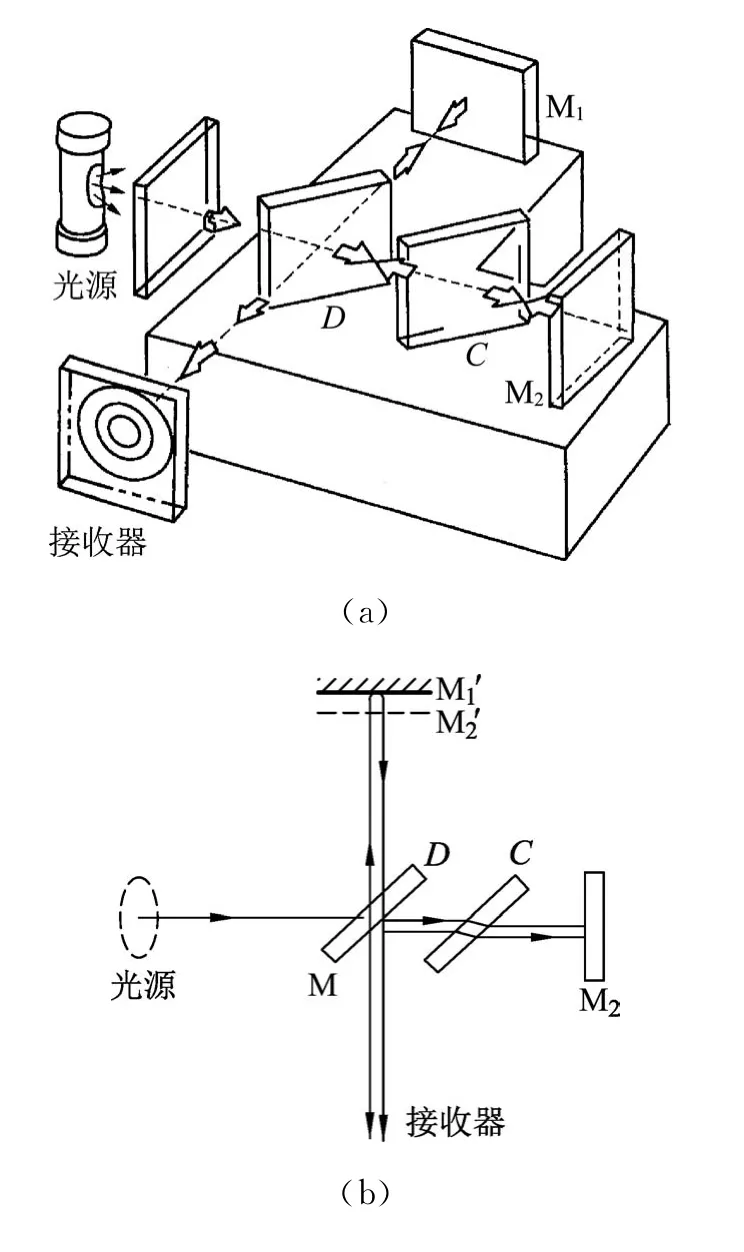
图4
(1)此干涉图样是等倾干涉还是等厚干涉?设光源的波长为λ,两臂上反射镜M1和M2到半反半透镜M的距离之差为t.试求屏上k级亮环的半径rk.条纹疏密分布如何?
(2)若用钠光灯(含有λ1=589 nm 和λ2=589.6 nm两条分立的谱线)照明迈克尔逊干涉仪,只考虑中心附近的干涉条纹.首先调整干涉仪得到最清晰的干涉条纹,然后移动M1,干涉图样逐渐变得模糊.至第一次干涉现象消失时,M1由原来位置移动了多少距离?
(3)若光源的光谱为589 nm到589.6 nm的连续谱,只考虑中心附近的干涉条纹,则能看到的最高干涉级数为多少?此时两臂的距离差是多少?(光路如图5所示)
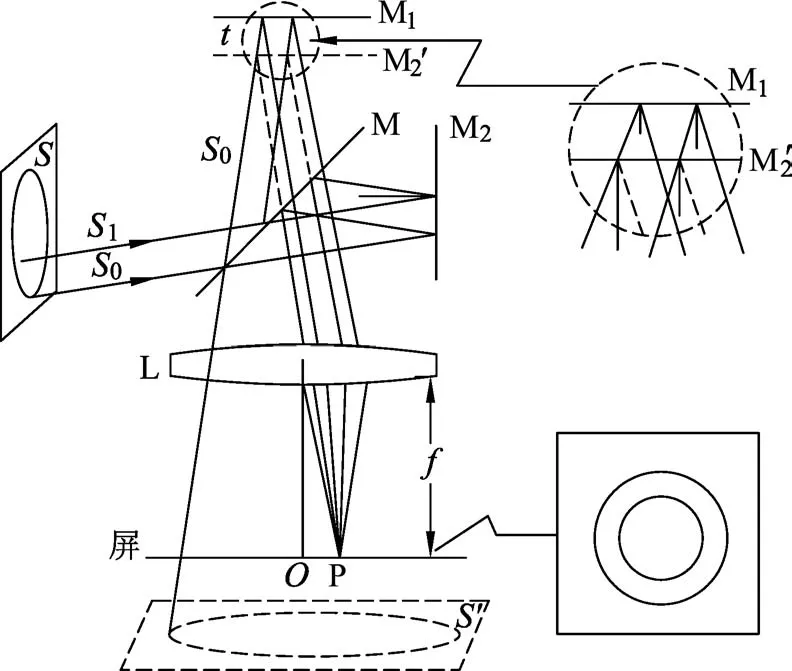
图5
解析:(1)根据前面对迈克尔逊干涉仪知识的讲解,可知干涉图样是一系列同心圆环时,属于等倾干涉.在 M1和 M2′空气薄膜处光程差2t cosθ,θ为空气薄膜内折射角.



赏析:第(1)问属于基本问题,考生应当熟练掌握.第(2)(3)问实际上是以迈克尔逊干涉仪为载体考核干涉的基础理论,请注意,第(2)问考核的是两单色光谱干涉消失问题,第(3)问改为连续光谱求最大干涉消失的级次问题,所要求的光程差条件完全不同.这些内容比较抽象,需要考生仔细研读相关教材,真正弄懂才能顺利求解.
题2.(第38届中学物理竞赛决赛实验题试题的B部分)如图6所示,迈克尔逊干涉仪利用分束镜G1将入射光束分成两束,两束光分别经过两个反射镜M1和M2反射到分束镜处合束后,在空间相干叠加形成干涉图样.反射镜M1可沿导轨前后移动改变位置.图7为其实物图.如用白光扩展光源照射并适当调节干涉仪,可实现白光的等厚干涉.

图6 迈克尔逊干涉仪光路图

图7 迈克尔逊干涉仪实物图
B1.在反射镜M1和M2偏离相互垂直状态一个微小角度α时,转动大转轮移动M1镜,在两路光束光程相等(此时M1镜位置为d0)附近可观察到白光等厚干涉的彩色直条纹.分别顺时针和逆时针转动转轮寻找出现彩色直条纹的准确位置,这两种情况下图7中大转轮读数窗的读数是否相同?请说明原因.在d0位置时,调小夹角α,干涉条纹有何变化?
B2.在d0位置时,调节α角尽量小,再在M1镜前平行放置一平板玻璃(忽略平板玻璃反射),白光的干涉条纹消失.此时换成激光扩展光源照明,能观察到圆环条纹,进一步微调α角直至圆环条纹不随眼睛观察位置变动而发生吞吐.在放置平板玻璃前,通过眼睛看到的M1和M2镜的相对位置为:(a)M1镜离眼睛更近;(b)M2镜离眼睛更近;(c)M1和M2镜重合.放置平板玻璃后,通过眼睛看到的M1和M2镜的相对位置为:(a)M1镜离眼睛更近;(b)M2镜离眼睛更近;(c)M1和M2镜重合.
此时,若大范围移动M1镜远离观察者,圆环条纹吞吐情况如何,两臂之间的光程差如何变化?若反方向大范围移动M1镜,结果又是如何?
B3.假定移动M1镜离开d0位置,使得条纹吞进,直至整个视场呈现完全均匀亮度,此时M1镜位置为d1,其位移量为Δ=|d1-d0|,请给出折射率n用玻璃板厚度t和Δ表示的关系式.若分别用σt和σΔ表示t和Δ的不确定度,请给出用t、Δ、σt和σΔ表示的n的不确定度.已测得Δ=(2.776±0.005)mm,平板玻璃厚度t用螺旋测微器测量结果如表1所示,螺旋测微器零点读数为0.009 mm,允差为0.004 mm,允差满足均匀分布.请分别计算出t和n的测量结果及其不确定度.

表1 平板玻璃厚度测量实验数据
解析:B1.由于精密螺纹的螺纹间距(就是齿轮与齿轮之间由于咬合上存在空隙),往回倒转大转轮,就会造成回程误差.所以顺时针和逆时针转动时大转轮读数窗的读数不同.在d0位置时,调小夹角α,由于微小放大作用,干涉条纹会变粗变稀疏.
B2.放置平板玻璃前,用白光进行等厚干涉来确定等光程交棱位置,所以M1和M2镜的相对位置为重合.放置平板玻璃后,相当于拉近M1与分束板的位置(类似于河底变浅),所以M1镜离眼睛更近.当调节M1镜远离观察者,观察者直观上认为空气薄膜厚度先变小后变大,所以干涉条纹先吞后吐.如果单从光程角度分析,M1镜前插入玻璃增大了该条光路的光程,所以当 M1镜远离时,光程差一直增大.若开始向观察者大范围移动M1时,相当于空气薄膜间距一直增大,所以干涉条纹一直吐出,光程则先减小后增加.


赏析:这道实验题全面地考查了干涉仪的原理、操作和数据处理,对于考生有一定的难度.B1中的等厚干涉,当平移反射镜M1时,干涉条纹只有左右移动;当改变镜面间夹角时,干涉条纹既有疏密变化,又会看到整体平移效果.B2中插入玻璃板后,我们会感觉到调节M1在玻璃板中的视觉距离导致的圆环吞吐似乎与课堂上讲的光程差的变化之间有矛盾,具体地说,就是从视觉上看,调节反射镜M1的像与M2的像再次重合过程,实际是M1光路与M2光路的光程差不断增大的过程,所显示的现象是圆环吞进,而我们课堂上分析和演示的现象却是M1光路与M2光路的光程差减小时圆环吞进,光程差增大圆环吐出.之所以这样,是因为插入玻璃板后,迈克尔逊干涉仪条纹级数不再是圆环中心最大,而是圆环边缘更大,这就容易理解为什么光程变大条纹反被吞进去的原因了.

