基于MATLAB的机械臂运动学分析和轨迹规划

马艳艳，曾台英，江海林

基于MATLAB的机械臂运动学分析和轨迹规划

马艳艳，曾台英，江海林

（上海理工大学，上海 200093）

研究包装机械臂运动学和轨迹规划，以实现机器臂的平稳运行和精确控制。以六自由度包装机械臂模型为研究对象，采用改进的D–H参数法建立坐标系，推导运动学方程，运用MATLAB搭建机械臂模型并进行正逆运动学仿真，以验证模型的正确性。其次，采用五次多项式插值算法对机械臂关节空间进行轨迹规划。最后，针对包装作业中待包装产品的定点抓取搬运任务进行轨迹规划和仿真。搭建的机械臂模型正确，五次多项式插值法轨迹优化效果好，可保证各关节角度、速度和加速度曲线光滑连续；计算出抓取搬运任务中各关节的关节量，并得到了末端执行器运动轨迹曲线。机械臂能以预期的运动精度完成抓取搬运的动作，为进一步探究机械臂的运动控制和实际应用奠定了基础。

六自由度机械臂；包装机械；轨迹规划；多项式插值法

在包装行业中，包装机械占据着十分重要的位置。在某种程度上，包装机械水平直接决定了整个包装行业的发展水平[1-2]。传统的手工包装作业由于劳动强度大、生产效率低、质量不稳定等缺点已经无法满足人们日益增长的生产生活的需要，因此，机械臂以其智能、高效、安全等优点在包装作业中得到了越来越广泛的应用。由于抓取搬运等工序对包装流水线的高效工作非常重要，因此对机械臂的要求也越来越高[3-5]。

为了提高机械臂的运动精度和稳定性，对其进行运动学分析和轨迹规划是机器人技术的核心内容之一，国内外很多学者在这一领域进行了研究。付香雪等[6]基于标准D–H法对包装分拣机械手进行了运动学分析和轨迹规划，结果表明建立的运动学方程正确可行，仿真所获得的数据可以应用到实际机械臂的运动控制中，实现准确、可靠的运行。孙绍杰等[7]基于多项式插值对机械臂轨迹规划方法进行了研究，结果表明插值算法实现了机械臂的轨迹规划要求。Parikh等[8]以五自由度机器人为例研究了利用六次多项式计算多自由度机器人的光滑轨迹方法，可减少对末端执行器的冲击，保护关节免受机械振动。Guo等[9]使用直接方法来获得最佳轨迹规划和最大动态载荷，提出了一种五自由度混合动力机械臂的容量算法。文中以六自由度机械臂为研究对象，利用改进的D–H参数法建立机械臂的运动模型，用MATLAB搭建机械臂仿真模型并进行正逆运动学分析，最后用多项式插值算法进行关节空间轨迹规划，并对实际工程应用进行仿真验证，以期为进一步探究机械臂运动的精确控制和实际在包装自动化中的应用奠定基础。

1 包装机械臂运动学分析

1.1 机械臂D–H模型

文中以某六自由度包装机械臂为研究对象，该机械臂是串联开链式机械臂，见图1。坐标系{0}是基坐标系，其中坐标系{0}和坐标系{1}重合，坐标系{3}和坐标系{4}重合，轴2、轴5和轴6相互平行，轴1和轴3相互平行。已知两轴朝向，可由右手法则确定第三轴[10]。

考虑到改进的D–H方法有着便于建模和计算的优点，文中在描述相邻连杆和相邻关节的相对位置关系时采用了改进的D–H方法建立坐标系。与原D–H方法相比，改进D–H方法坐标系前置，即改进的D–H方法是描述连杆−1至连杆的相对位置关系[10]。按照改进D−H方法，确定六自由度机械臂的改进D−H参数，见表1。

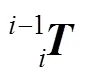
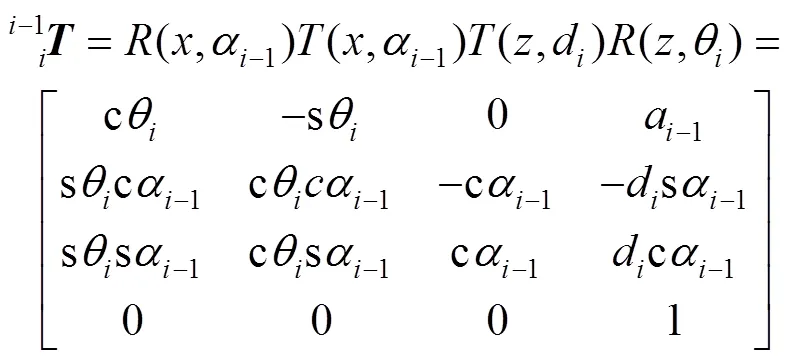
表1 六自由度机械臂改进D–H参数

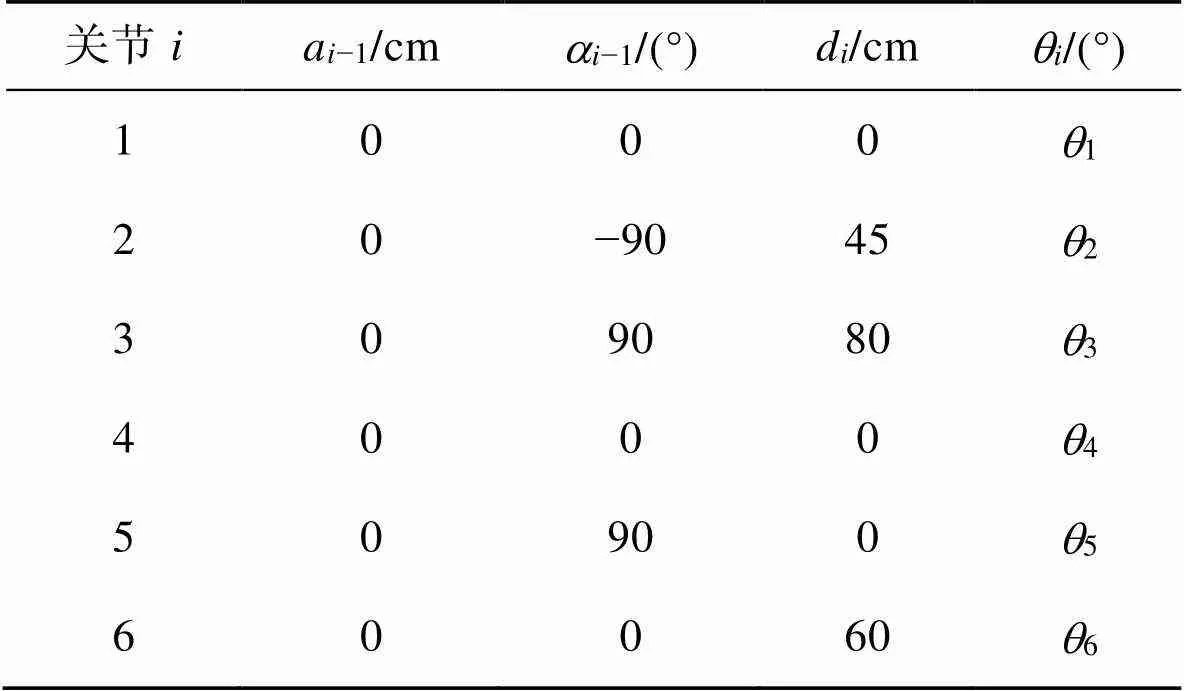
Tab.1 Modified D-H parameter for 6-DOF manipulator

将表1中各关节参数代入式（1）可得各个关节的变换矩阵，然后将这些变换矩阵相乘，则可得基坐标系和末端执行器间的变换矩阵为：

由式（2）可得坐标系{6}相对于坐标系{0}的变换矩阵，通过计算可以获得机械臂末端执行器的位姿。

1.2 MATLAB仿真模型及正逆运动学分析

根据改进的D–H参数，用MATLAB Robotics Toolbox工具箱搭建包装机械臂仿真模型。机械臂初始状态时，各关节参数为0，机械臂末端空间位置为（0, −105, 80），建立的机械臂仿真模型见图2。

对模型进行正运动学分析，起始点位置为[0 0 0 0 0 0]，终止点位置为[3×π/4 π/8 0 π/5 π/6 0]。用正运动学求解指令fkine解得初始点位姿矩阵a见式（3），终止点位姿矩阵b见式（4）。

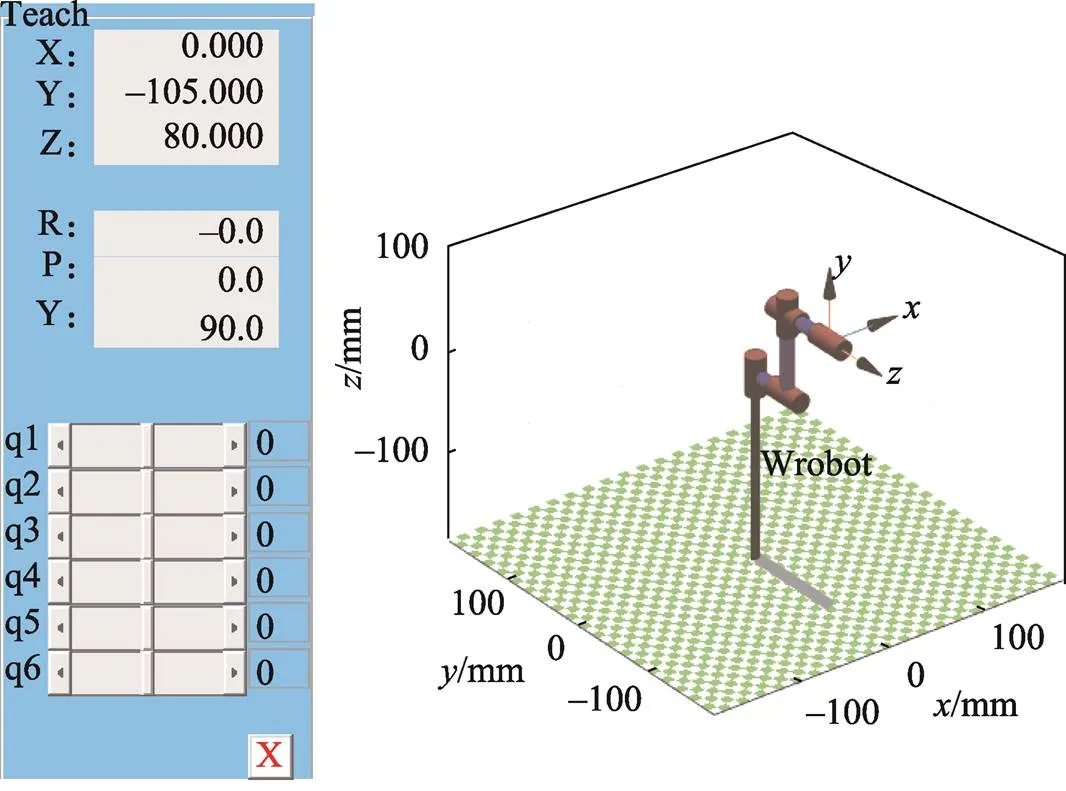
图2 机械臂仿真模型

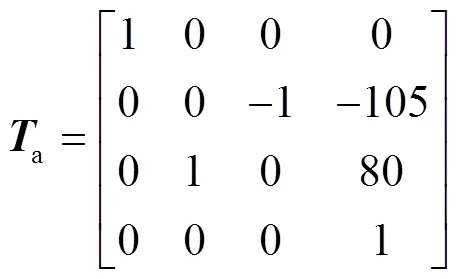
对模型进行逆运动学分析，用逆运动学求解指令ikine来求解各个关节的角度，起始位置的关节角度a=robot.ikine（a），终止位置的关节角b=robot.ikine（b），将其输入到Matlab命令窗口解得：a=[0 0 0 0 0 0]，b=[2.356 2 0.392 7 0.314 2 0.314 2 −2.879 8 −2.879 8]。结果表明关节角a与起始点位置相一致，关节角b与起始点位置不一致，再对关节角b进行正运动学分析可得位姿矩阵c，且c=b。结果表明，对逆运动学计算求出的关节角再进行正运动学求解得出的位姿矩阵c与正运动学求解得出的位姿矩阵b一致，从而验证了机械臂的参数设定和仿真模型是正确的。

2 机械臂轨迹规划

机械臂的轨迹规划目的是在完成作业任务的过程中，保证各个角关节变量的位置、速度及加速度函数曲线是连续的，且在起点和终点位置的速度和加速度均为零。通过轨迹规划可实现机械臂的平稳运动，减少振动和冲击，保证其运动轨迹精度的同时还可以避免额外的能量消耗，减少机械部件磨损，提高运动稳定性和准确度，从而提高作业的效率和任务完成的效果。

机械臂轨迹规划可分为笛卡尔空间轨迹规划和关节空间轨迹规划，由于笛卡尔空间轨迹规划要进行逆运动学求解得出各关节的关节角，求解不便，而关节空间的轨迹规划通过控制各个关节角的规划轨迹，可实现机械臂的实时控制[11-12]。根据包装作业的要求，机器人的轨迹规划为点到点运动，因此，可采用关节空间轨迹规划，通过控制各个关节角来实现机械臂的实时控制。

2.1 多项式插值法

关节空间轨迹规划是用逆运动学方法将笛卡尔空间中的路径点转换为其对应的关节角，然后用插值计算法计算机械臂的各个关节插值点，使其各个关节同步并且顺滑地到达目标点。现在进行轨迹规划时大多采用多项式插值计算方法中的三次多项式和五次多项式插值函数。由于低于三次函数的插值方法的阶次低，求导得到的加速度是常数，故无法保证加速度轨迹的连续性，而高次多项式插值函数的阶次过高会使插值区间两端出现大幅度的纵向波动[13]。利用三次多项式插值法得到的机械臂运动的关节角度、角速度是连续的，其缺点是没有对关节角加速度进行约束，因此其加速度有突变，且加速度的变化率很大，这会导致机械臂运动不稳定，机械系统会产生一定的冲击[14-15]。五次多项式插值法不仅对路径起点和终点的角度和角速度进行约束，还对角加速度有约束，故可保证关节角度、角速度和角加速度的光滑连续。综上，五次多项式插值法为关节空间轨迹规划的理想算法[16]。

已知在初始和终止时刻的关节位置、速度和加速度，则可采用五次多项式保证关节角度、角速度以及角加速度的光滑连续，即[10]：

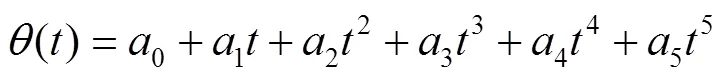
若初始关节和终止关节的角度、角速度和角加速度的6个约束条件为：

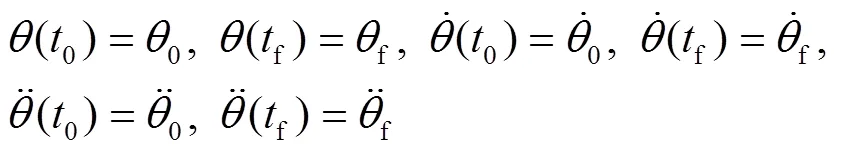
对式（5）求一阶导数可得角速度函数为：

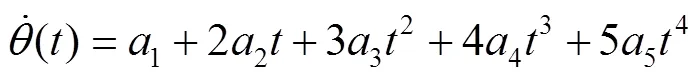
对式（5）求二阶导数可得角加速度函数为：

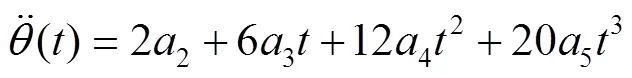
联立式（6）—（8）的方程组求解可得五次多项式系数为：

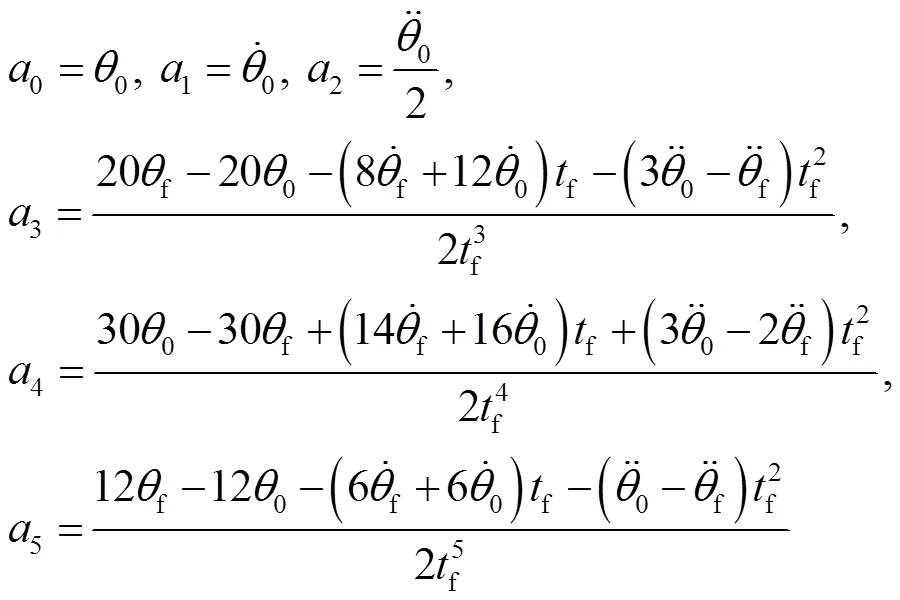
2.2 轨迹规划仿真结果与分析

上述机械臂从初始点（0 −105 80）到终止点（64.7 67.5 87.4）末端执行器的位移见图3。在0～2 s时，关节1角度从0°到135°，关节2角度从0°到22.5°，关节3和关节6角度不变，关节4角度从0°到36°，关节5角度从0°到30°。

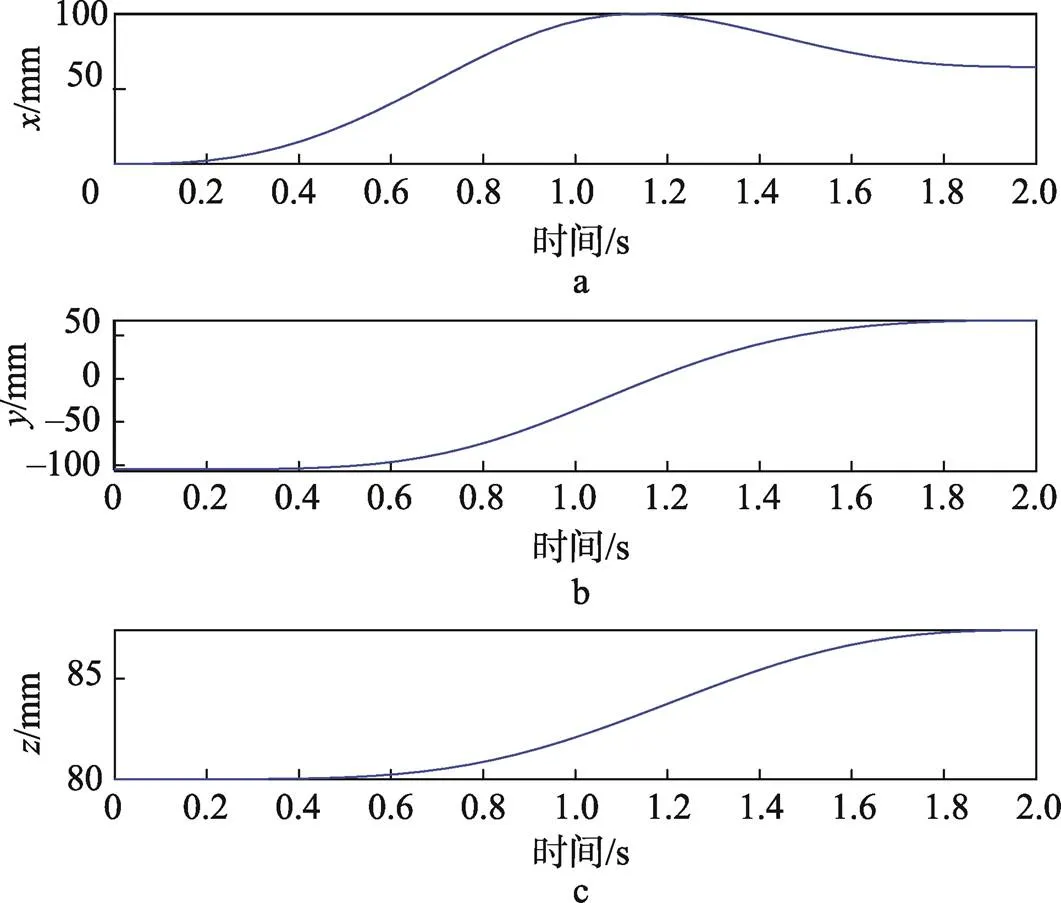
图3 末端执行器位移图

设初始时间=0 s和终止时间f=2 s，对各关节的关节角、关节角速度以及关节角加速度进行仿真分析，得到了机械臂的各关节位置、速度和加速度变化的曲线图，结果见图4—6。

从图4—6中可以看出，各关节的启停角速度、角加速度均为零，机械臂各关节位置、速度和加速度曲线均光滑连续，得到的各关节最大角度、角速度、角加速度差别不大。关节3和关节6不转动，关节1、2、4和5在运动过程中角速度先从零逐渐增大到极值，然后又逐渐减小到零，而关节角加速度有2个方向相反的极值点，运动过程中加速度先从零增大到极大值后减小，又反方向增大到极值后再减小到零，说明机械臂的运动是一个先加速后减速的过程。符合机械臂实际运动过程中加速度先增大后减小的实际情况。因此，仿真分析结果与实际使用情况相符合。

从机械臂各关节位置、角速度和角加速度的仿真结果表明，五次多项式插值法轨迹规划使得各个关节角的角度、角速度以及角加速度呈光滑连续的曲线，运动时期无突变现象，机械臂从初始点运动到终止点的过程中，各关节运动平稳，无冲击和振动，各关节性能良好。综上，可以证明前面所建立的模型正确，且五次多项式插值法优化效果好，能够较好地解决关节空间轨迹规划的问题，同时也验证了多项式插值法的有效性，确保了机械臂较高的工作效率和平稳性。

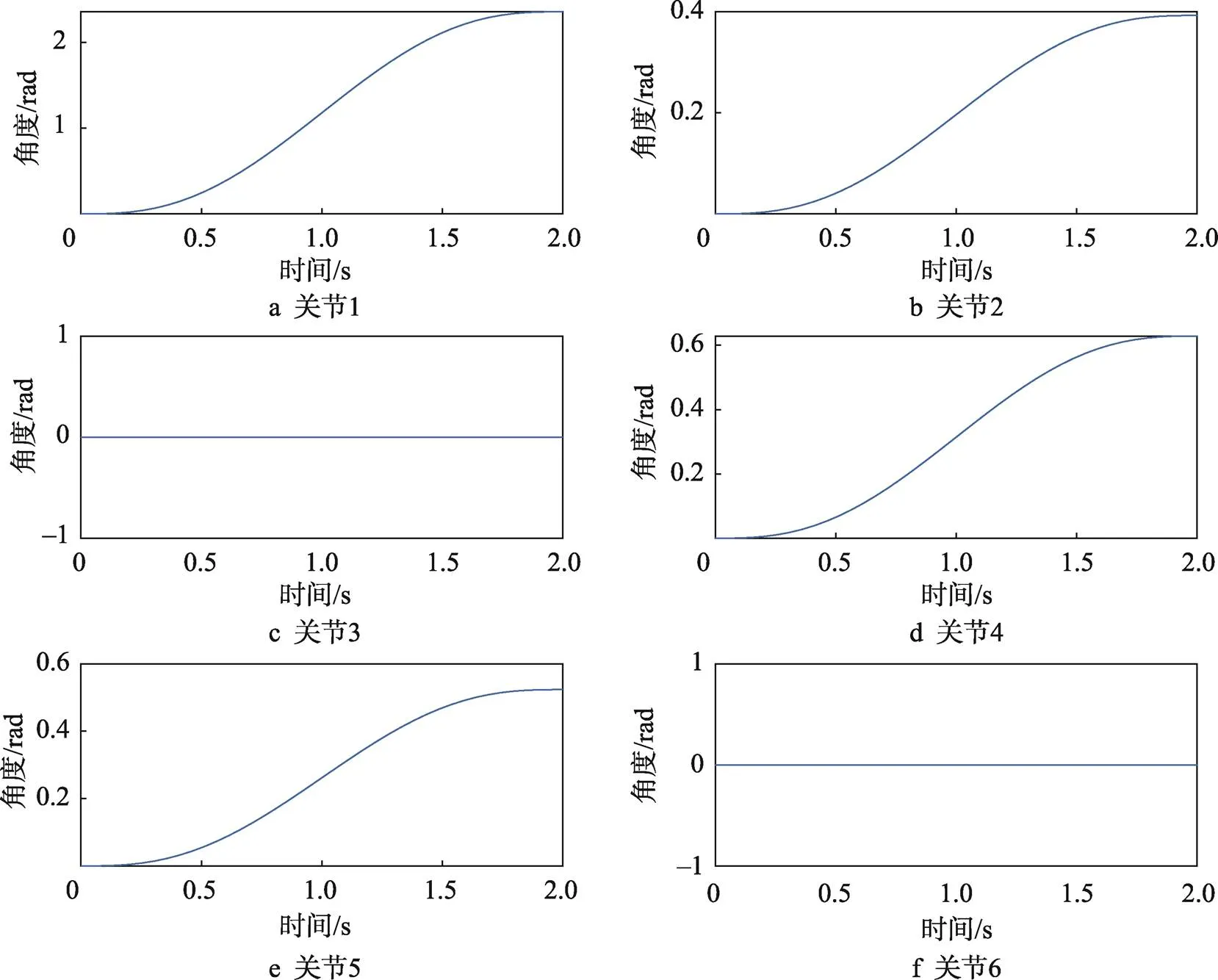
图4 各关节位置曲线

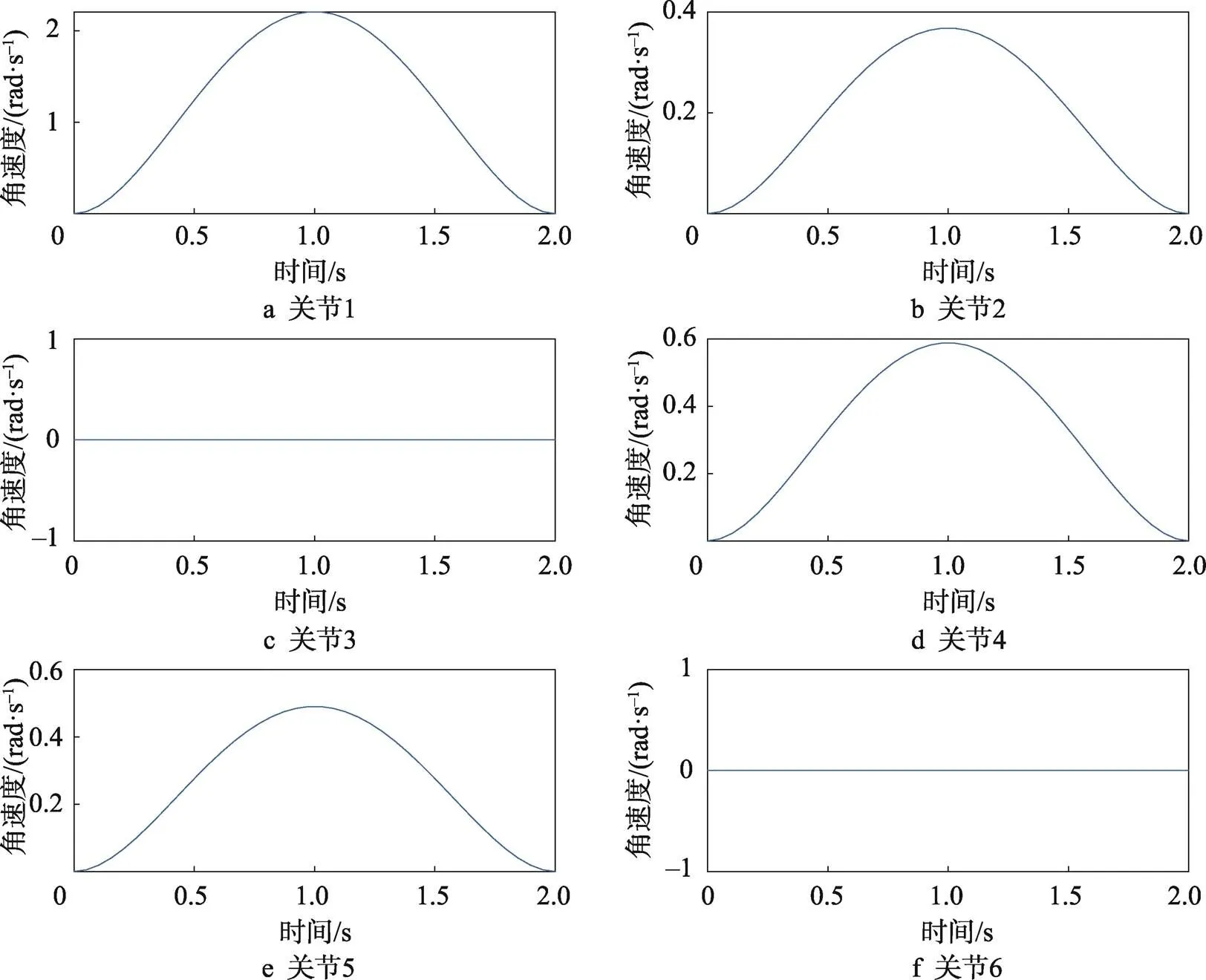
图5 各关节角速度曲线

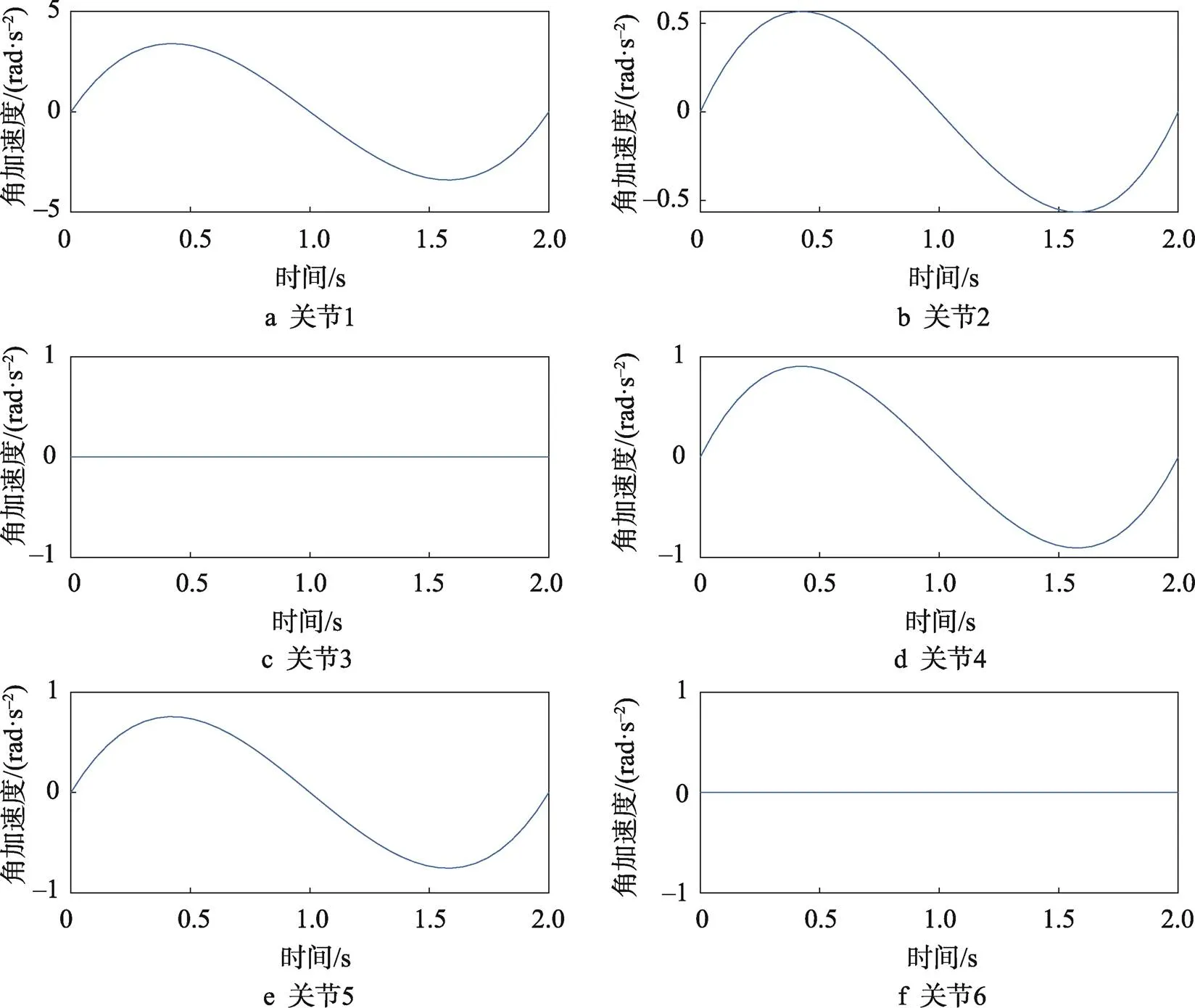
图6 各关节角加速度曲线

3 机械臂轨迹运动试验

在实际的工程应用中，包装作业中常使用机械臂运送流水线传送带上的产品，即将传送带上的产品搬运到目的点处，这种情况下机械臂运行轨迹的起始点和终止点均是固定的，可采用PTP点位作业。设计一个模拟生产线上的定点抓取搬运任务，给定4个关键路径点，机械臂用来搬运固定位置的工件，送至固定位置的存放点。现以机械臂的基坐标系为参考坐标系，设待包装产品起始点位置为1，将产品搬运到目标点4的位置，给定2个中间路径点2、3，机械臂抓取点目标和其位置坐标见表2。根据MATLAB进行仿真计算各关节的关节量，由逆运动学求解可得各路径点关节空间的变量值，见表3。机械臂执行器末端位置的运行轨迹见图7。仿真结果证明了轨迹规划的正确性，表明机械臂能以预期的运动精度完成待包装产品的抓取搬运工作。

表2 抓取点位置坐标

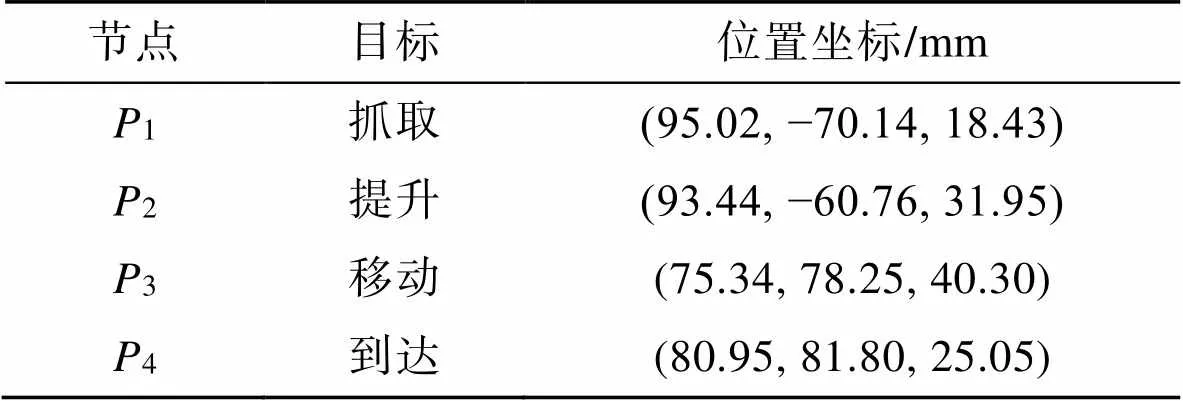
Tab.2 Position coordinate of grabbing point

表3 关节路径点

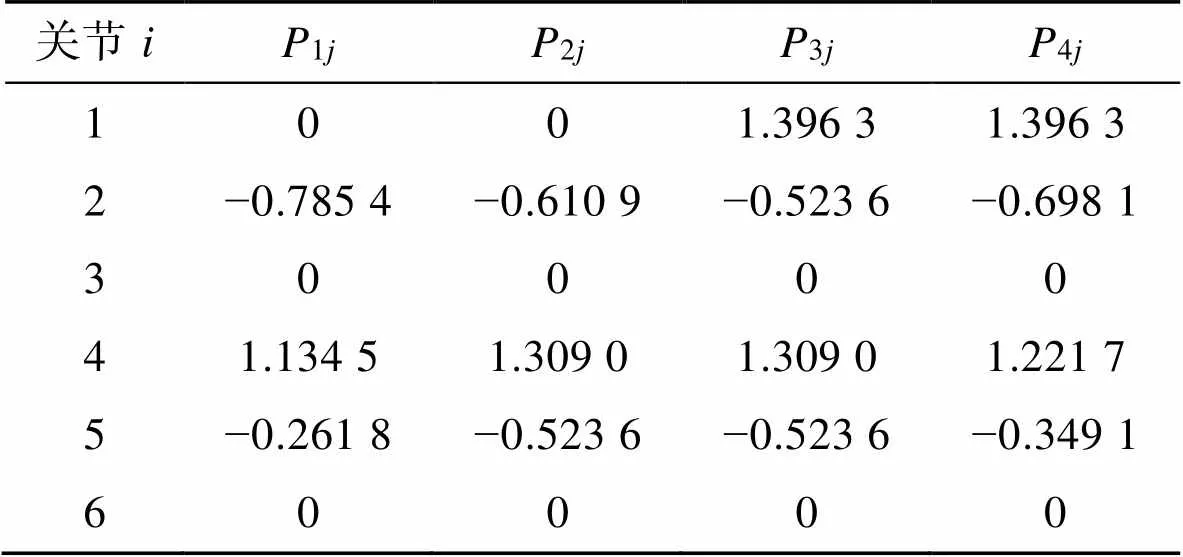
Tab.3 Joint path point

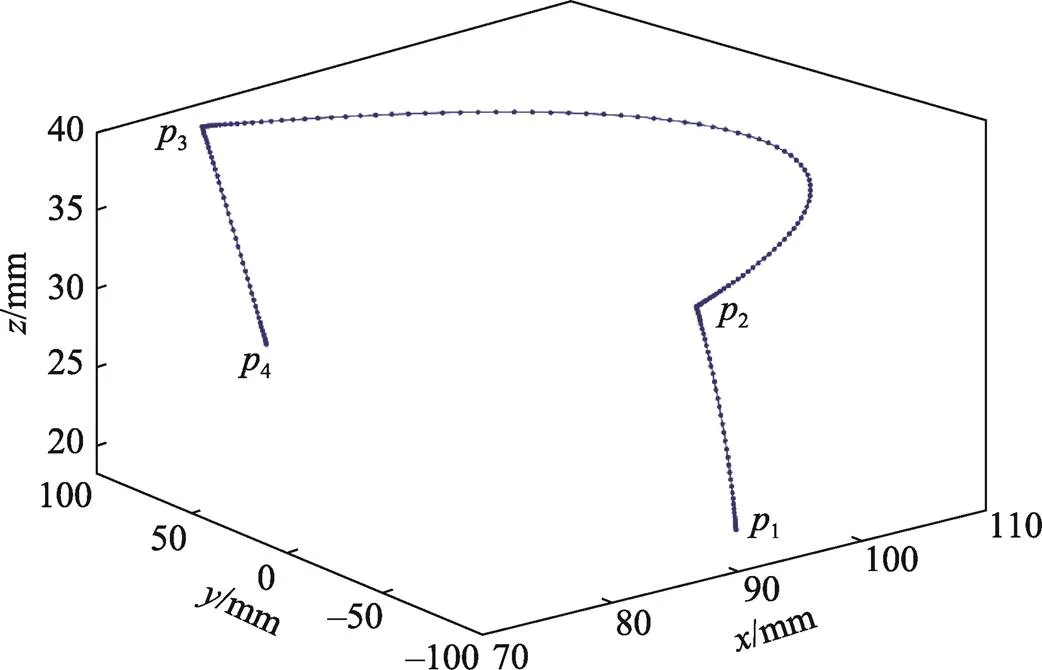
图7 末端执行器运动轨迹曲线

4 结语

以六自由度机械臂为研究对象，首先采用改进的D–H参数法建立了坐标系，推导运动学方程，运用MATLAB搭建机械臂仿真模型并进行正逆运动学分析，验证了模型的正确性。其次，采用五次多项式插值算法对机械臂关节空间进行了轨迹规划，给定机器人初始位姿和终止位姿，对末端执行器的运动轨迹进行分析，得到了各关节的运动曲线、角速度曲线和角加速度曲线，并对仿真结果进行了分析。结果表明，五次多项式插值法优化效果好，各个关节角的角度、角速度以及角加速度呈光滑连续的曲线，运动过程中加速度先增大后减小，运动时期无突变现象，能够很好地解决关节空间轨迹规划的问题，同时也验证了五次多项式插值算法的有效性，确保了机械臂较高的工作效率和运动平稳性。最后针对包装作业中的待包装产品的定点抓取搬运任务，根据MATLAB进行仿真计算各关节的关节量，并得到了末端执行器运动轨迹曲线。仿真结果表明，机械臂能够以预期的精度完成抓取搬运作业，达到预期运动精度和平稳性的要求。机器臂轨迹规划的顺利完成，可保证机械臂在作业环境中运动平稳和安全可靠，为机器臂的平稳、实时和精确控制奠定了理论基础，对机械臂后续用于包装作业具有一定的理论意义和工程应用价值。

[1] 温景阳, 杜宇凡, 秦涛, 等. 基于Dobot机械臂的包装自动线运动规划与仿真[J]. 包装工程, 2021, 42(21): 231-238.

WEN Jing-yang, DU Yu-fan, QIN Tao, et al. Motion Planning and Simulation of Automatic Packaging Line Based on Dobot Manipulator[J]. Packaging Engineering, 2021, 42(21): 231-238.

[2] 曹华, 李伟. 基于遗传算法的包装机械臂位置精度控制方法[J]. 包装工程, 2021, 42(9): 249-253.

CAO Hua, LI Wei. Position Accuracy Control Method of Packaging Manipulator Based on Genetic Algorithm[J]. Packaging Engineering, 2021, 42(9): 249-253.

[3] 李宪华, 范凯杰, 疏杨, 等. 六自由度模块化机械臂的轨迹规划与仿真[J]. 制造技术与机床, 2018(9): 73-77.

LI Xian-hua, FAN Kai-jie, SHU Yang, et al. Trajectory Planning and Simulation of Six Degrees of Freedom Modular Manipulator[J]. Manufacturing Technology & Machine Tool, 2018(9): 73-77.

[4] 梅江平, 臧家炜, 乔正宇, 等. 三自由度Delta并联机械手轨迹规划方法[J]. 机械工程学报, 2016, 52(19): 9-17.

MEI Jiang-ping, ZANG Jia-wei, QIAO Zheng-yu, et al. Trajectory Planning of 3-DOF Delta Parallel Manipulator[J]. Journal of Mechanical Engineering, 2016, 52(19): 9-17.

[5] 郑涛, 刘满禄. 一种机械臂分段插值轨迹规划方法[J]. 机械设计与制造, 2020(3): 261-264.

ZHENG Tao, LIU Man-lu. A Method of Segmental Interpolation Trajectory Planning for Robotic Arm[J]. Machinery Design & Manufacture, 2020(3): 261-264.

[6] 付香雪, 韩顺杰, 张冬冬, 等. 基于D–H法的包装分拣机械手运动学分析和轨迹规划[J]. 包装与食品机械, 2018, 36(5): 47-50.

FU Xiang-xue, HAN Shun-jie, ZHANG Dong-dong, et al. Kinematics Analysis and Trajectory Planning of Package Sorting Manipulator Based on D-H Method[J]. Packaging and Food Machinery, 2018, 36(5): 47-50.

[7] 孙绍杰, 齐晓慧, 苏立军, 等. 基于多项式插值的五自由度机械臂轨迹规划方法研究[J]. 机电一体化, 2011, 17(11): 33-37.

Sun Shao-jie, Qi Xiao-hui, Su Li-jun, et al. Trajectory Planning of 5 - DOF Manipulator Based on Plynomial Method[J]. Mechatronics, 2011, 17(11): 33-37.

[8] PARIKH P A, TRIVEDI R R, JOSHI K D. Trajectory Planning of a 5 DOF Feeding Serial Manipulator Using 6th Order Polynomial Method[C]// Journal of Physics: Conference Series, Bristol, 2021.

[9] GUO Wan-jin, LI Rui-feng, CAO Chu-qing, et al. A New Methodology for Solving Trajectory Planning and Dynamic Load-Carrying Capacity of a Robot Manipulator[J].Mathematical Problems in Engineering, 2016, 1302537: 1-28.

[10] 韩建海. 工业机器人[M]. 4版. 武汉: 华中科技大学出版社, 2019: 1-5.

HAN Jian-hai. Industrial Robot[M]. 4th ed. Wuhan: Huazhong University of Science and Technology Press, 2019: 1-5.

[11] BOURBONNAIS F, BIGRAS P, BONEV I A. Minimum-Time Trajectory Planning and Control of a Pick- And-Place Five-Bar Parallel Robot[J]. IEEE/ASME Trans Mech, 2015, 20: 740-749.

[12] ZHANG Xiao-qing, MING Zheng-feng. Trajectory Planning and Optimization for a Par4 Parallel Robot Based on Energy Consumption[J]. Applied Sciences, 2019, 9: 1-19.

[13] GIL A, REINOSO O, MARIN J M, et al. Development and Deployment of a New Robotics Toolbox for Education[J]. Computer Applications in Engineering Education, 2015, 23(3): 443-454.

[14] LI Xian-hua, LYU Lei, SHENG Rui, et al. An Effective Construction Method of Modular Manipulator 3D Virtual Simulation Platform [J]. 3D Research, 2018, 9(24): 1-12.

[15] 李琳琳, 寇子明, 吴娟. 六自由度机械臂的设计与轨迹规划研究[J]. 煤矿机械, 2019, 40(8): 43-46.

LI Lin-lin, KOU Zi-ming, WU Juan. Research on Design and Trajectory Planning of Six Degrees of Freedom Manipulator[J]. Coal Mine Machinery, 2019, 40(8): 43-46.

[16] 王文坛. 机械臂轨迹规划及动力学研究[D]. 济南: 山东大学, 2017: 31-34.

WANG Wen-tan. Research on Trajectory Planning and Dynamics of Manipulator[D]. Jinan: Shandong University, 2017: 31-34.

Kinematics Analysis and Trajectory Planning of Manipulator Based on MATLAB

MA Yan-yan, ZENG Tai-ying, JIANG Hai-lin

(University of Shanghai for Science and Technology, Shanghai 200093, China)

The work aims to study the kinematics and trajectory planning of packaging manipulator to achieve smooth operation and accurate control. With 6-DOF packaging manipulator model as research object, the coordinate system was established by the modified D-H parameter method, and the kinematics equation was deduced. Based on MATLAB, the manipulator model was built and direct and inverse kinematics simulation was carried out to verify the correctness of the model. Secondly, a quintic polynomial interpolation algorithm was used to plan the trajectory of joint space. In the end, the trajectory planning and simulation was carried out for the fixed-point grabbing and carrying tasks of the products to be packed in the packaging operation. The model of the manipulator was correct, and the trajectory optimization effect of the quintic polynomial interpolation method was good, which could ensure smooth and continuous angle, velocity and acceleration curves of each joint. The joint parameters in grabbing tasks were calculated and the trajectory curve of the end-effector was obtained. The manipulator can complete grabbing and carrying tasks with expected precision, which lays a foundation for further research on the motion control and practical application of the manipulator.

6-DOF manipulator; packaging machinery; trajectory planning; polynomial interpolation method

TB486；TP242.2

A

1001-3563(2023)03-0187-07

10.19554/j.cnki.1001-3563.2023.03.023

2022−03−13

马艳艳（1977—），女，博士，副教授，主要研究方向为机械设计与机器人技术。

责任编辑：曾钰婵