自行封装的烟草打包装置机械式均载控制技术
范 忠,熊 涛,刘礼欲,胡晓蕾
(湖北中烟工业有限责任公司恩施卷烟厂,湖北 恩施 445099)
0 引言
在20世纪80年代以前,国内烟草企业逐渐发展,在企业发展初期,通常按照生产自动化方向为主进行设计,使得生产加工更为简便[1],但这种模式下,并没有为烟草输送自动化预留合理的外部条件,使得企业在后续改进过程中存在条件差等问题。后来随着部分烟草企业的改建[2],大多数企业统一设计生产与物流自动化模式,使自动化烟草机械具有更大的应用前景,同时,随着烟草机械的快速发展,机械的自动化程度也日益完善[3],其中,烟草打包装置在烟草的物流传输自动化过程中显得尤为重要,但打包装置在日常运行过程中,通常存在运动速度、加速度难以精确控制等问题[4],导致烟草打包效率变低。为此,盛凯等[5]研究青贮秸秆高压缩比打包机压缩装置的控制,但该控制方法不适用于烟草打包装置,且在控制后依然存在较高的电机故障现象;张秀丽等[6]研究烟草颗粒肥配比混施装置控制,但该控制技术应用后仍然无法提高烟草打包产量。
总结以往研究经验,本文提出自行封装的烟草打包装置机械式均载控制技术,采用幂函数速度曲线算法实现烟草打包装置电机的均载控制。
1 烟草打包装置机械式均载控制
1.1 自行封装的烟草打包装置设计
由于现有烟草打包方法操作时间过长,耗费人力过多,导致打包效率低下[7-8],为此设计一种自行封装的烟草打包装置,如图1所示。

图1 自行封装的烟草打包装置
在自行封装的烟草打包装置中,主要利用电机实现整体运行。在装置横向设置压紧平台,在该平台上方设计移动式压紧面板,并将液压杆放置在压紧面板两侧,通过液压缸驱动液压杆,使该液压杆可以完成竖向移动[9-11],带动压紧面板同时可以竖向移动。在压紧面板下端面,与压紧平台的上端面对齐,并在压紧平台外侧装置第1竖向板,该板与平台上端面对齐;同时在第1竖向板的上端面中,均匀装置连接帽嵌置孔,在孔内装置连接帽,在压紧面板外侧装置第2竖向板,其下端与压紧面板下端平齐,并在该竖向板下端装置连接销嵌置槽,在槽内装置连接销,且每个连接销均与连接帽相对应,在2个竖向板的下端与上端长度之和与设想打包的烟草厚度相等。
1.2 自行封装的烟草打包装置同步控制系统
本文采用PLC控制器搭建烟草打包装置的控制系统,实现该装置的打包控制任务。PLC控制器可实现自动控制[12-13],完成烟草的自动打包,其可以控制烟草打包装置完成烟草的输送和打包等工作,全部动作程序均按照PLC控制自动完成。该烟草打包装置控制器的工作流程如图2所示。

图2 烟草打包装置控制系统流程
根据图2可知,在烟草打包装置控制程序中,采用多流程控制,因此,需采用均载控制技术对打包装置电机进行控制。
1.3 自行封装的烟草打包装置机械式均载控制方法
由于自行封装的烟草打包装置在日常运行时速度较高,使得装置在启动与制动过程中伺服电机对装置造成冲击[14-15],导致烟草打包装置出现机械式故障。为此,本文提出烟草打包装置同步控制技术,使装置机械式均载得到控制,以降低烟草打包装置的齿轮磨损程度,从而延长装置使用时间。
1.3.1 机械式均载控制技术
按照力学中的定轴转动理论,若刚体按照固定轴进行转动,则刚体在进行转动时产生的转动惯量与固定轴的角加速度相乘,可以得出刚体沿固定轴转动时的合外力矩,具体计算式为
(1)
J为刚体的转动惯量;ω为角速度;β为角加速度;M为合外力矩。烟草打包装置采用电机驱动齿轮,因此针对齿轮进行研究。在合外力矩中,主要包含电机驱动力、机械传动装置齿轮摩擦力等,推导式(1)能够得出
(2)
θ为转动角度。对式(2)两边积分,可得
(3)
通过式(3)可以计算得到,当刚体处于定轴转动时,转动动能产生的增量与刚体产生合力矩过程中制造的功相等。因此,在某一时间段内合外力矩对齿轮所做的功一致,即在该时间段内,齿轮转动时的动能变化率未出现变化,说明在进行齿轮加减速时烟草打包装置受到的冲击为均载冲击。设转动动能为E,则式(4)成立,即
(4)
K、J为常量值,则ωβ为常量,即通过常量值可以描述刚体角速度与角加速度的乘积时,转动动能变化率不会发生变化,在此时满足均载冲击。利用如下方法判定启停算法能否满足均载冲击。
1.3.2 基于幂函数速度曲线的启停速度算法
在当前工业装置控制系统中,几乎都需要使用加减速算法来控制机械运动状态。传统控制系统中通常会选用梯形速度曲线实现控制,本文采用幂函数速度曲线,对烟草打包装置机械式均载进行控制。

(5)
根据式(5)可知,其中第2项存在t变量,因此当C1不等于0且C3等于0时,ωβ才属于不等于0的常量,在此时,可以获取启动烟草打包装置电机时的角速度函数为
(6)

(7)
式(7)中,第2项包含t变量,因此当P1不等于0且P3等于0时,ωβ才属于不等于0的常量,在此时,可以获取制动状态下烟草打包装置电机角速度函数为
(8)
若电机处于正常运行,则时间t的增加不会改变角速度ω,所以在此时,将正常运行状态下的角速度ω设为常量B。同时,将式(6)和式(8)中常量C1、C2、P1、P2依次设为C、-t1、P、t4。此时,角速度曲线方程为
(9)
B、C、P均为常数;Δt1为电机启动时间,由t-t1计算;Δt2为电机制动时间,由t4-t计算。



通过以上幂函数曲线算法,可以实现电机启动、制动时的均载控制,且实时性较高,可在较短的时间内快速响应达到正常运转状态。
2 实验分析
将本文技术应用至烟草加工领域,对本文技术的烟草打包装置均载控制能力进行分析。
分析应用本文控制技术控制打包装置后,装置运行期间的连续维修时长以及停机次数,分析结果如表1所示。
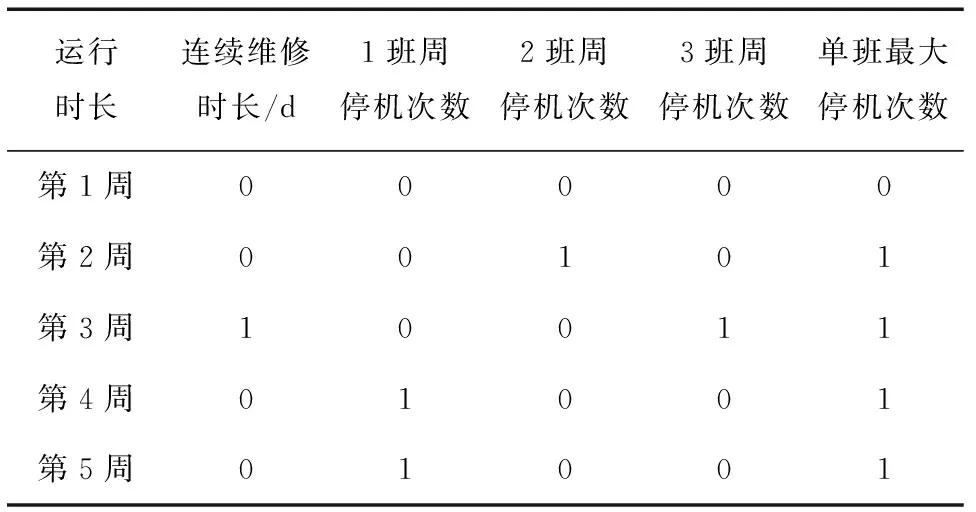
表1 装置运行期间的停机次数分析
根据表1可知,应用本文技术后,每个烟草打包班组仅在第3周出现1 d的维修,在其他运行周期内均未出现维修情况,说明本文技术可有效降低装置运行故障,减少维修概率,同时,每班组停机次数较少,单班最大停机次数每周仅为1次,说明应用本文技术后可减少停机次数,保障装置正常运行。
分析应用本文技术前、后烟草打包后的密度与产量,分析结果如图3所示。
根据图3a可知,在应用本文技术前,烟草打包后的打包密度明显较低,说明打包过程中比较浪费存储空间,而应用本文技术后,打包密度的得到一定提升,使得烟草打包更为牢固;由图3b可知,在初始烟草喂入量下,应用本文技术前后的烟草产量几乎一致,但随着烟草喂入量的增加,未应用本文技术时的产量上升幅度较小,而应用本文技术后产量迅速提升,说明采用本文技术控制烟草打包装置可有效提高打包时的产量。
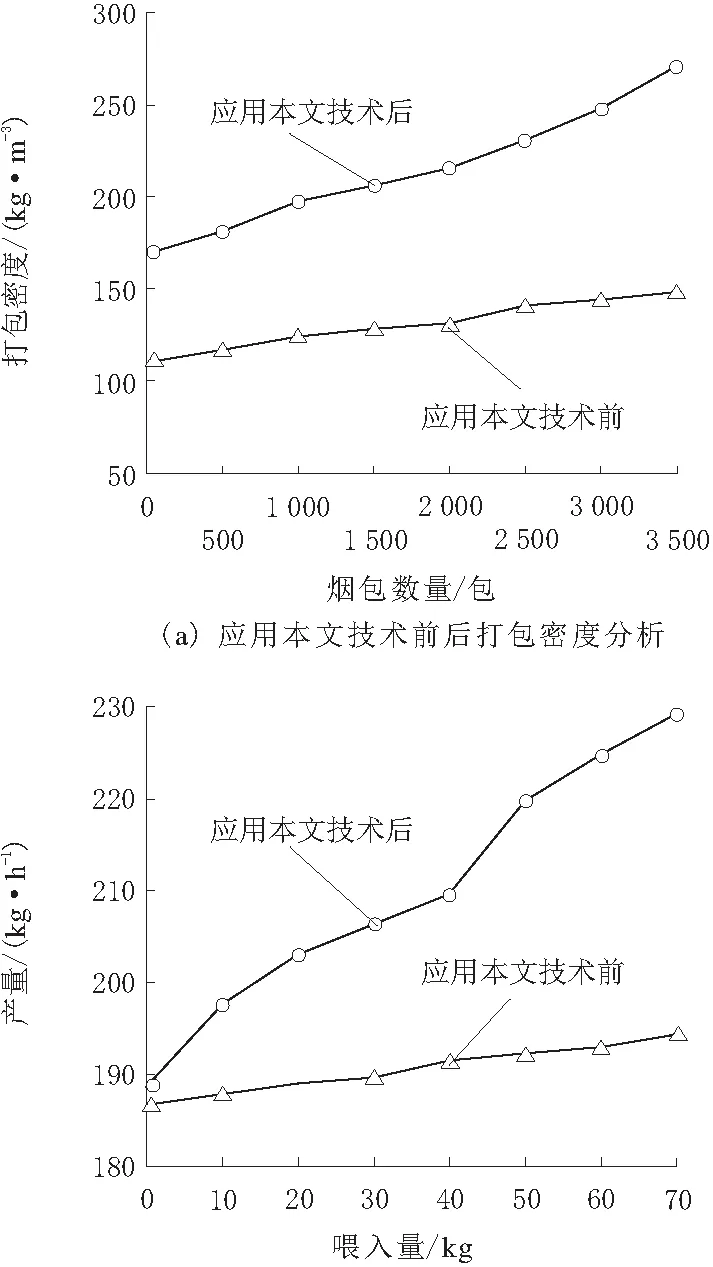
图3 烟草打包情况分析
利用本文技术对烟草打包装置进行均载控制,假设烟草打包装置的驱动轴扭矩正常运行在20 kN·m左右,分析应用本文技术控制前、后装置驱动轴扭矩在不同时间下的变化,分析结果如图4所示。
根据图4a可知,在应用本文技术前,烟草打包装置的驱动轴扭矩在不同运行时间下的波动范围较大,始终在5~30 kN·m之间波动,而应用本文技术后,装置驱动轴扭矩的波动范围几乎在20 kN·m左右,说明应用本文技术后可有效保障烟草打包装置的驱动轴扭矩更加稳定。
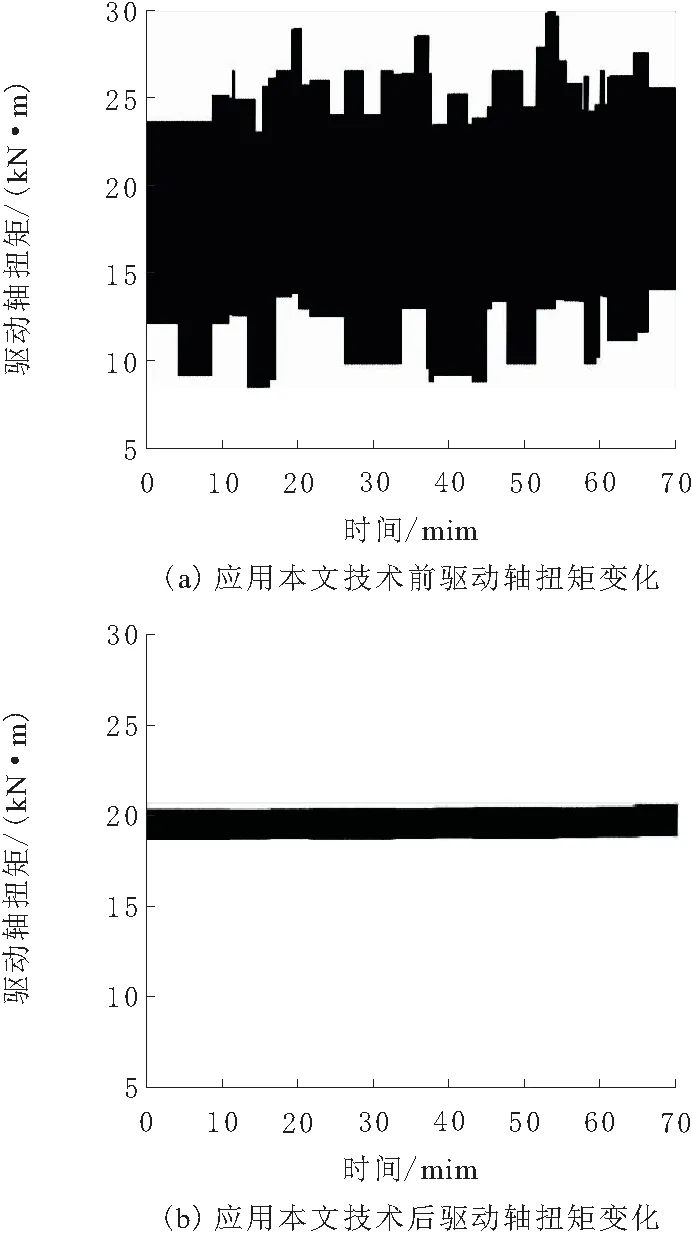
图4 应用本文技术前、后装置驱动轴扭矩变化情况
分析应用本文控制方法后烟草打包装置电机的负载扭矩变化,假设在装置运行30 min时,将负载扭矩从8 kN·m调整为10 kN·m,分析本文技术能否对装置主、从电机进行有效控制,分析结果如图5所示。

图5 主、从电机负载扭矩控制能力分析
根据图5可知,应用本文技术后,主从电机均能够在所需时间内完成负载扭矩的调整,由此说明本文技术具有较高的均载控制能力。
3 结束语
研究自行封装的烟草打包装置机械式均载控制技术,构建制动状态下的烟草打包装置电机角速度函数,判断烟草打包装置的电机能否承受不同大小的均载冲击,将均载控制技术与基于幂函数速度曲线的启停速度算法相结合,进行自行封装的烟草打包装置机械式均载控制,保证控制烟草打包装置运行期间的停机次数较少,解决了烟草打包过程操作时间过长,耗费人力过多的问题。
但是本文技术的研究与应用过程尚未提及在打包速度、上料过程控制方面的优势,烟草打包装置的运行效率验证结果还需完善。

