考虑光伏调频的新型电力系统频率态势预测

茆 超，张冲标，毕江林，陈金威

(国网浙江省电力有限公司嘉善县供电公司，浙江 嘉兴 314199)

0 引言

随着双碳目标的提出，中国电网的发电物理架构正在飞速的发生改变[1-2]。其中，电网源侧发电资源的低碳、高清洁化逐渐成为趋势[3]。以光伏为代表的可再生能源大规模应用使得传统煤炭污染、高能耗、高成本问题得到了有效缓解。然而，高比例同步发电单元的被替代措施使得电力系统的传统惯量迅速下降，带来了众多电力系统频率稳定性问题[4]。2016年南澳“9.28”大停电、2019年英国“8.9”大停电等事故都是归因于新能源电力系统高占比新能源机组导致的惯量支撑能力不足。因此，如何预测分析高比例光伏并网后运行的频率安全稳定问题亟需研究。

当前，针对电网源侧发电单元主动参与调频的研究较为丰富。文献[5]提出灵活利用负载变化控制，基于离散的电气数据将减载率参考值转变为光伏直流电压参考值，通过光伏阵列的调节实现电网有功调制；文献[6]提出一种自适应控制策略，定量分析虚拟惯量大小与频率变化率的关系，利用区间分析对频率实现调整；文献[7]提出附加功率环和调压算法，以调频功率为研究对象，使用步长跟踪方式实现对功率动态、稳态性能的提高，从而提升电力系统的频率稳定性；文献[8]提出考虑光伏单元P-U外特性，结合常规虚拟惯量控制对电力系统频率进行控制。

然而，针对光伏参与调频的电力系统频率态势研究较为匮乏。本文基于传统火电频率响应模型，考虑光伏附加频率控制单元，分析了光伏参与调频的新型电力系统频率特性。首先建立了传统电力系统频率响应模型及光伏单元频率响应模型，综合各调频单元的控制方式建立了考虑光伏参与调频的电力系统频率响应模型。利用模型分析法对多资源参与调频下的电力系统频率特征进行定量分析，计算了系统频率特性传递函数、初始频率变化率及稳态频率误差。最后通过MATLAB/Simulink仿真平台对本文所提光伏参与电力系统频率特性进行验证。

1 电力系统频率响应模型

随着新能源的大规模渗透[9-10]，众多电力电子器件被应用，因而电力系统物理架构逐渐呈现出复杂化与电气量解耦的特性[11-12]。当前，为分析新型电力系统下的频率稳定性，针对电力系统频率特性的分析方法主要分为3类，分别为时域仿真法[13]、模型分析法[14]及人工智能算法[15]。其中，模型分析法利用低阶简化模型将电力系统的频率动态响应过程通过多阶数学表达式量化表示。本文在传统频率响应模型的基础上，建立光伏参与调频下的电力系统频率响应模型。

1.1 传统电力系统频率响应模型

传统电力系统频率响应模型保留了同步发电机的相关控制参数[16]，并基于电力系统的频率传递特性，建立同步发电机调速器工作下P-f的数量关系，如图1所示。其中，H为系统等效惯性时间常数,D为阻尼常数，PL为负荷消耗有功大小，R为一次调频下垂系数，FH为原动机高压缸做功系数，TR为再热时间常数，km为机械功率因数，Psp为电力系统冲击负荷占系统总负荷的比重，Pm为机械功率，Δωg为同步机频率扰动量，s为拉氏算子。

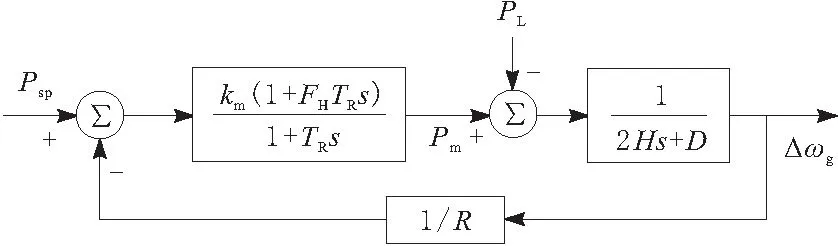
图1 传统电力系统频率响应模型

根据图1可计算从负荷扰动ΔPL到频率扰动Δωg的传递函数为

(1)

ωn为无阻尼自然频率；ζ为阻尼比；Go为比例系数；zo为原动机再热时间常数的倒数。

且满足

(2)

若电力系统出现负荷有功阶跃扰动，则电网频率s域表达式为

(3)

ωd为阻尼自然频率；fpu为电网频率的参考值(标幺值)，fref_pu=1/s；G(s)/s为频率扰动值(标幺值)。

(4)

对式(3)进行拉普拉斯逆变换，得到电网频率的时域下的频率表达式为

(5)

A为幅值；β为相位，且

(6)

1.2 光伏调频频率响应模型

1.2.1 光伏常规虚拟惯量调频频率响应模型

光伏的常规惯量控制策略通过锁相环动态特性实现，锁相环控制下的频率为

(7)

Utq为逆变器端电压的q轴分量；kp、ki为锁相环控制参数。

根据式(7)可得有功功率ΔPPV1增量为

(8)

即

ΔPPV1=2HPV·Δf·s

(9)

HPV为光伏虚拟惯量时间常数。

因此，若光伏只采用常规虚拟惯量控制方式时，其频率模型传递函数为

(10)

1.2.2 考虑P-U外特性的光伏调频频率响应模型

当光伏阵列与低压直流电容相连时，通过改变电容电压可实现光伏阵列输出功率的变化。为此，设计光伏阵列运行于最大功率点的左侧。利用线性化拟合手段，其输出功率P2为

P2=aUpv+b

(11)

a、b为拟合系数。

将式(11)线性化处理得

ΔPPV2=a·ΔUpv=a·k·Δf

(12)

k为控制系数。因此，若光伏只采用该调频策略时，其频率响应模型传递函数为

(13)

1.2.3 综合虚拟惯量控制及P-U外特性的光伏调频频率响应模型

本文光伏采用双极式发电结构，其中存在一个高压直流电容Cb，同时在逆变器电压外环中引入f-Udc频率弥补环节。参考文献[8]所提双极式发电的高压直流电容电压方程为

(14)

Cb、Udc、Udczero、Pdc、Pg分别为高压直流电容、高压直流电压、高压直流电压初始值、直流输出功率、光伏发电输出功率。

对式(14)线性化处理得

(15)

ΔPpv、ΔUdc分别为光伏单元功率变化量、高压直流电压变化量。

根据式(14)和式(15)可得光伏发电单元频率响应模型传递函数为

(kpvCbUdczero+Hpv)·s

(16)

kpv为光伏单元时间常数。

光伏单元频率响应模型如图2所示。

图2 光伏单元频率响应模型

1.3 光伏参与调频的电力系统频率响应模型

新能源发电单元的渗透使得电网调频资源对非同步发电单元的考虑逐渐增加。本文考虑传统火电及光伏同时参与电力系统有功调制，从而实现系统调频。如图3所示为考虑光伏参与调频的电力系统频率响应模型。

图3 聚合电力系统频率响应模型

由图3可知电力系统频率、功率的数量关系为

(17)

当电网出现功率扰动ΔPL时，电力系统功率变化量为

ΔP=-ΔPL-ΔPpv-ΔPR=

-ΔPL-{Gpv(s)+GR(s)}·Δf

(18)

GR(s)为传统火电频率响应传递函数，且满足

(19)

2 光伏参与调频的电力系统频率态势预测

2.1 电力系统频率特性模型

利用模型分析法，基于经典的低阶电力系统频率相应模型，考虑传统同步发电机、光伏参与调频，建立新能源参与调频下的电力系统频率响应模型。根据式(17)和式(18)可得电力系统频率特性传递函数为

(20)

由式(20)可得电力系统频率变化频域表达式为

Δf(s)=Gsys(s)·ΔPL(s)=

(21)

其中，A为关于频域微分算子s的多项式，且满足

A=kpvCbUdczero+Hpv+2H

(22)

2.2 初始频率变化率定量分析

当电力系统出现扰动时，根据初值定理(式(23))计算光伏参与调频下的电力系统频率初始变化率，即

(23)

(24)

由式(24)可知，光伏发电采取双极式发电且在外环中引入f-Udc频率弥补环节，当发生一定的功率扰动时，电力系统初始频率变化率与光伏响应系数、高压直流电容、直流电压初始值、光伏单元时间常数和电力系统惯性时间常数有关，即电力系统初始频率变化率只与光伏调频单元控制参数及系统等效惯量有关。

图4是根据式(24)所得的初始频率变化率三维因素图，且初始频率变化率值为标幺值。

图4 电力系统初始频率变化率三维因素

由图4可知，系统等效惯性时间常数、光伏惯性时间常数越大，电力系统频率初始变化率绝对值越小。

2.3 电力系统稳态特性定量分析

稳态频率误差直接反映了电力系统的稳态频率特性，基于终值定理(式(25))定量计算在受到功率扰动后的电力系统稳态频率误差。

(25)

(26)

根据式(26)可知，稳态频率误差与火电一次调频下垂系数有关，但是与光伏调频单元的控制系数无关。

考察负荷阻尼大小对电力系统频率的影响。根据式(26)对阻尼系数求导，即

(27)

根据式(27)推导结果可知，当ΔPL大于0时，稳态频率误差对阻尼系数D的偏导大于0，即随着阻尼系数的增加，电力系统的稳态频率误差值大小增加。根据式(26)可知，当同步发电机一次调频下垂系数、阻尼系数、功率扰动值都大于0时，电力系统稳态频率误差值小于0。因此，可知随着阻尼系数的增加，电力系统稳态特性相应提高。

3 算例仿真

基于MATLAB/Simulink建立考虑光伏调频的新能源电力系统频率响应模型。光伏模块采用双极式光伏发电结构，逆变器采集高压侧直流电容的动态特性来模拟同步发电机的惯量响应，低压直流电压维持在定值且光伏阵列输出功率的稳态值不变。分析不同工况下电力系统的频率特性变化，负荷为1 000 MW，风电额定功率为200 MW，负荷扰动为60 MW(0.06 pu)。

3.1 光伏参与调频下电力系统频率特性分析对比

为验证光伏参与调频的可行性，对2种情况下频率特性进行定量分析，考察不同调频方式下电力系统的频率偏差情况。

风电场风速恒定，各机组参数如表1所示。

表1 系统参数设定值

不同调频方式下电力系统频率变化如图5所示。

图5 不同调频方式下系统频率曲线

由图5可知，相较于传统同步发电机单独调频，光伏参与调频下的电力系统频率稳定性更强，最大频率偏差绝对值减小，且最大频率偏差时间点延迟；光伏参与调频下其稳态频率误差没有变化，因此在电力系统趋于稳定时，稳态频率误差与光伏调频控制参数无关，即光伏调频单元不参与电力系统调频。

3.2 光伏惯性时间常数对电力系统频率的影响分析

讨论在传统同步发电机组、新能源光伏机组参与调频控制参数确定时，光伏惯性时间常数对电力系统频率变化率的影响。

其中，传统火电机组、新能源机组调频控制参数参考表1，设置光伏惯性时间常数分别为2 s、4 s、6 s，考察不同光伏惯性时间常数下的电力系统初始频率变化率、最大频率偏差时间等相关电力系统频率特征指标，结果如图6所示。

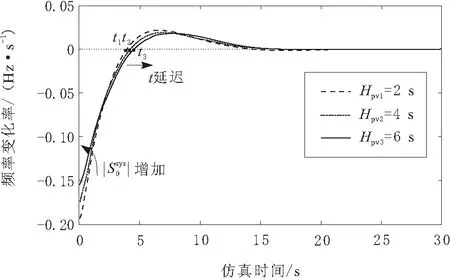
图6 不同光伏惯性时间常数下系统频率变化率曲线

由图6可知，随着光伏惯性时间常数的增加，电力系统初始频率变化率绝对值减小；光伏惯性时间常数增加，t1

3.3 阻尼系数对电力系统频率的影响

随着负荷侧频率响应能力的提升，新型电力系统的源荷协调能力得到加强，设置不同电力系统阻尼系数，通过仿真分析电力系统的频率稳定性。其中，传统火电机组、新能源机组控制参数参照表1，分别设置不同等效惯性时间常数D分别为2、4、8，系统仿真波形如图7所示。

图7 不同阻尼系数下系统频率曲线

由图7可知，随着负荷阻尼系数的增加，电力系统初始频率变化率绝对值不变，即初始频率变化率的大小与负荷阻尼系数无关；随着电力系统阻尼系数的增加，稳态频率误差绝对值减小，即光伏参与调频模式下电力系统稳态频率特性提升；当光伏参与传统电力系统调频控制时，阻尼系数的增加使得最大频率偏差减小，且最大频率偏差时间提前。

4 结束语

针对新型电力系统频率稳定问题，本文考虑了光伏参与电力系统频率调节，通过理论定量分析、仿真验证了光伏参与调频控制策略下电力系统频率稳定性的影响因素，研究结果表明：

a.传统同步发电机、光伏单元联合参与调频控制策略下，电力系统频率较单一火电调频控制策略更加稳定，新能源光伏参与调频的控制策略是可行的。

b.光伏参与调频下的电力系统初始频率变化率与光伏调频单元控制参数及系统等效惯量有关；在机组控制参数确定时，负荷阻尼系数的提升可减小电力系统初始频率变化率绝对值，同时可提升电网稳态频率，增加电网的频率稳定性。