电梯导轨校准机器人力位控制研究
汪 洋,俞建峰,俞俊楠,蒋 毅,化春键,钱陈豪
(1.江南大学机械工程学院,江苏 无锡 214122;2.江苏省食品先进制造装备技术重点实验室,江苏 无锡 214122)
0 引言
随着国内建筑数量的不断增加,对电梯的使用需求量也逐年递增。电梯导轨的校准精度直接影响乘梯舒适性和安全性[1]。在机器人实际校准导轨的过程中,既需要考虑校准的精度,又需要控制校准力,以防止因校准力太大,固定导轨的支架出现断裂等安全问题。因此,需要研究一种机器人的位置/力控制策略,有效控制导轨的位置精度和校准力的大小。
目前,在机器人的位置/力控制策略[2]中,优先保证位置精度,同时控制机器人接触力的算法鲜有。因此,本文设计了一种基于改进的粒子群-模糊PD的力位控制系统,并应用在电梯导轨校准机器人中,期望力可以根据位置控制要求实时调整,并且可根据机器人当前运动状态灵活切换控制模式。研究结果表明,本文所提出的控制策略可以同时保证力和位置的跟随精度,并且调整精度满足国家标准对电梯导轨垂直度偏差范围的规定。
1 控制系统方案
当电梯导轨校准机器人处于不同的工作空间时,要对末端执行器的控制需求进行相应调整。当机器人在无约束空间运动时,应着重调整末端执行器的位姿,让其按照规划好的参考轨迹进行运动,以便快速、准确地到达目标导轨位置;当机器人末端执行器夹持住导轨,进行导轨的校准时,需要控制校准精度的同时控制导轨的校准力,使校准力满足期望的接触力,以便使末端执行器与导轨之间保持一定的柔顺性,在稳定可控的期望力下,快速、灵敏地实现校准目的。本文控制系统如图1所示。

图1 电梯导轨校准机器人力位控制系统
图1中,基于改进的粒子群算法和模糊PD(improved particle swarm optimization-fuzzy PD,PsoFuzzyPD)的电梯导轨校准机器人力位控制方案由位置内环和阻抗外环组成。位置内环采用粒子群优化模糊PD+前馈动态控制,模糊控制器的输入为机器人关节转角误差和机器人关节角速度误差,先通过改进粒子群算法寻找PD控制器的kP和kD参数的初值,之后通过模糊自整定技术自调节PD控制器的kP和kD参数的值,以保证机器人位置控制的精度。
阻抗控制外环通过建立的机器人环境动力学模型,先将机器人末端实际位移x转换为末端实际接触力Fext,之后将Fext与机器人的末端期望接触力Fr的差值Fe输入至阻抗环节,输出调整量e修正机器人的期望运动轨迹,稳定控制电梯导轨校准机器人的末端实际接触力,从而确保电梯导轨调整时所受的校准力可控,保证机器人能高效、精准、可控并且安全地调整电梯导轨。同时,末端期望接触力根据实际调整需求进行限制,并设计PID调节器,通过参考轨迹xr与末端实际位移x的偏差进行末端期望接触力稳定的控制。对电梯导轨校准机器人的逆向运动学分析,将笛卡尔空间的参考轨迹xr经过修正后转换为机器人关节空间下的参考轨迹θr,输入至设计好的位置内环,保证在力跟踪稳定的情况下,提高机器人的位置控制精度。
2 机器人位置控制系统设计
基于动力学模型设计了改进粒子群优化模糊PD控制算法,使电梯导轨校准机器人的实际关节转角渐近收敛到期望关节转角,最终实现机器人的位置控制。
2.1 模糊PD+前馈控制器设计
以课题组自主设计的5轴关节型电梯导轨校准机器人为研究对象,由拉格朗日方程推导出机器人的动力学模型为

(1)
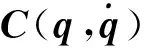
考虑到对各关节独立地使用PD控制这种线性反馈控制律,可以保证系统的渐进稳定性,因此控制器中引入PD控制。独立的PD控制率为
(2)
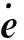
如果仅采用前馈控制,由于得不到反馈,受到扰动时关节转角一直会有跟随误差出现,仅采用PD控制则平衡不了系统产生的非线性误差[3],结合式(1)和式(2),得出此时机器人的控制方程为
(3)
(4)

(5)
kP0和kD0通过粒子群优化算法获得,且都为PD控制器中的初始参数;ΔkP和ΔkD为模糊控制器输出的参数修整值。
2.2 模糊化和模糊控制规则
2.2.1 输入变量及其模糊化

2.2.2 输出变量及其模糊化
模糊控制器的输出变量为比例增益的变化量ΔkP和微分增益的变化量ΔkD,量化后的论域分别取为[0,400]和[0,100]。输出变量在相应的论域上的参考模糊集定义为:NB(负大)、NM(负中)、NS(负小)、ZO(零)、PS(正小)、PM(正中)、PB(正大)。
2.2.3 模糊控制规则
模糊控制算法在PD+前馈控制器的基础上进行参数调整,并且基于整定原则以及专家经验[4],得到模糊控制器的输出曲面如图2所示。
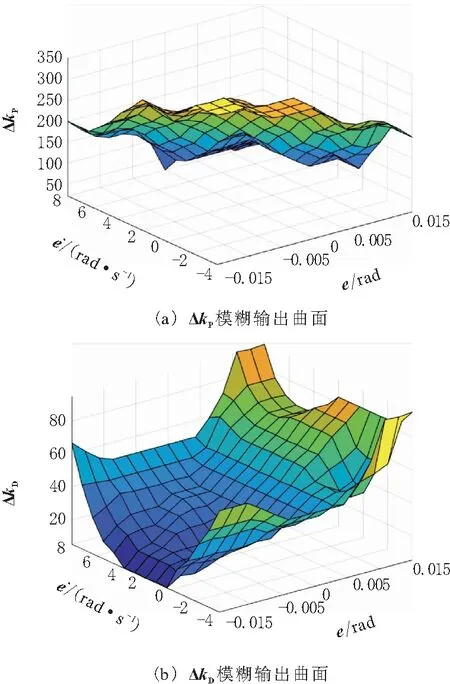
图2 模糊控制器输出曲面
2.2.4 精确化计算
先按照模糊规则表进行模糊决策,并通过重心法解模糊,最后通过式(6)确定机器人每个关节的比例增益和微分增益,填入ΔkP和ΔkD矩阵中。重心法计算式为[5]
(6)
z0为解模糊化后的准确值;zi为模糊论域内的值;uc(zi)为zi对应模糊规则中的隶属度值。
2.3 改进的粒子群算法优化模糊PD
传统的模糊PD控制(FuzzyPD)的kP和kD的初值都是人为选择的,完全依赖于经验知识和模拟调试的参数,很难达到预期的效果[6]。因此,本文采用改进的粒子群优化算法对模糊PD进行优化,选取机器人每个关节的比例和微分增益的初值,之后确定kP和kD的初值。
基本的粒子群算法容易陷入局部最优值,导致后面全局最优解收敛过慢,因此,本文采用带惯性权重的粒子群算法来提高粒子群的全局搜索能力,同时考虑模拟退火算法可以在初始温度选择和温度下降合理的条件下,能以一定的概率突跳并收敛到全局最优值,通过模拟退火算法改进粒子群算法,可以提高粒子跳出局部最优解的概率。
PsoFuzzyPD控制过程由初始化粒子群、适应度函数、位置和速度更新以及模拟退火过程7个步骤组成。优化步骤流程如图3所示。
a.对每个粒子的位置x和速度v进行随机初始化,粒子数本文取30。
b.计算每个粒子的当前适应度值ffit(xi),本文选择的适应度函数的表达式取误差绝对值积分型,表达式为
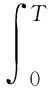
(7)
e(t)为t时刻机器人关节空间下,期望关节角度与实际关节角度的偏差;T为完成一次仿真花费的总时间。
c.计算个体的最优值(Pbest)和群体的最优值(gbest),每次迭代得到适应度值最优的个体极值存储在群体最优之中。
d.根据个体最优值和群体最优值,按照式(8)和式(9)对个体的速度vi和位置xi进行更新。
(8)
(9)
c1和c2为学习因子,通常为0到2之间;r1和r2为均匀分布的2个独立随机函数,随机生成0~1之间的实数;w为惯性权重因子。
e.判断粒子群优化过程是否达到全局最优或达到最大迭代次数,如果没有达到,重新返回步骤b,达到则执行模拟退火操作。
f.判断是否达到最低温度要求,若没有达到,则按照式(12)进行降温操作,根据式(10)进行温度初始化操作。若达到则直接输出结果。
g.随机生1个新的粒子种群,并且按照式(11)计算新解的接受概率,同时引入1个随机数,用来和新解的接受概率P比较,判断是否接受恶劣解,有利于增强算法跳出局部最优的能力,并代入式(8)和式(9)进行粒子的位置x和速度v的更新。
温度初始化公式为
Ttemp=-ffit(xi)/log0.2
(10)
每个粒子新解的接受概率P为
(11)
ffit(xi)和ffit(xi+1)为当前温度下目前粒子适应度值和新的粒子适应度值。
降温操作的公式为
Ttemp=γTtemp
(12)
本算法中γ取0.5。

图3 改进的粒子群算法流程
3 机器人基于位置的阻抗控制模型的建立
3.1 机器人阻抗控制模型
课题组设计的电梯导轨校准机器人调整导轨时,采用阻抗控制方法,将导轨与机器人末端夹持器的关系模型等效为质量-弹簧-阻尼物理系统,如图4所示。xe为导轨实际位置,Ke为环境刚度参数n×n维正定对角阵,x为机器人末端夹持器的实际位移,xr为末端夹持器的期望位置。二者之间产生的交互力Fext[7]为
(13)
z为机器人末端夹持器的实际位置;ze为末端夹持器夹持导轨时与环境接触时的初始实际位置,并且z和ze都是n×1维的矢量。

图4 机器人末端执行器与导轨之间的物理模型
机器人末端执行器与导轨之间的物理模型等效为
Fr-Fext
(14)
Fr为末端期望力;Md为惯性参数;Bd为阻尼参数;Kd为刚度系数。
阻抗控制的原理是将需要控制的末端交互力用等效阻抗代替,当电梯导轨校准机器人调整导轨,与导轨之间存在交互力时,接触处将产生阻抗力进行补偿,从而实现位置和力的动态交互与控制[8]。
在阻抗控制过程中,机器人从自由空间进入到受限空间时,机器人末端交互力需要实现过渡平滑,力误差响应快,超调量小。此时机器人的期望阻抗参数应满足[9]
(15)
当机器人运动实际位置满足阻抗控制需求时,通过末端实际接触力进行判别,并通过式(16)切换至阻抗控制,切换条件中的接触力阈值可以根据实际情况设定。
(16)
Fw为接触力阈值。
3.2 基于位置的阻抗控制方法
通过计算机器人与环境间的交互力,并结合式(14)的物理模型生成位置修正量,修正机器人的期望运动轨迹,内环的位置控制器则按照修正后的轨迹进行运动[10]。其中,反馈作用力Fe等于末端期望力Fr减去末端实际力Fext,位置修正量的频域表达式为
(17)
通过式(17)生成机器人的位置修正量e。位置修正量e对参考轨迹Zr修正后,生成机器人的控制轨迹Zd。当机器人和环境没有接触时,机器人正常运动,位置修正量e= 0,此时Zd=Zr。当机器人与环境进行交互时,此时e=Zd-Zr。
3.3 末端期望力自校正方法
机器人的末端期望力在导轨实际校准过程中,并不能提前知晓,因此,需要根据校准精度要求对机器人末端期望力实时调节,并且限制校准力的大小,所以建立末端期望校准力的模型为
(18)
KP为比例增益对角矩阵;KI为积分增益对角矩阵;KD为微分增益对角矩阵;Frmax为允许的最大期望力大小,可根据实际情况调整。
末端期望力经过阻抗控制环节,使末端校准力稳定可控,并且根据机器人末端位置误差实时调整校准力的大小,以保证导轨校准精度。
4 仿真实验分析
为了验证本文所提出的基于粒子群-模糊PD的电梯导轨校准机器人力位控制策略的有效性和可靠性,将利用MATLAB的Simulink仿真模块进行模拟。仿真对象为本课题组自主设计的5轴关节型电梯导轨校准机器人,电梯导轨校准机器人连杆参数如表1所示,ai为连杆长度,αi为连杆扭角,di为连杆偏置,θi为关节转角,其中,连杆参数为:a1= 0.14 m,a2= 0.35 m,a3= 0.32 m,d1= 0.134 m,d5= 0.108 m。

表1 电梯导轨校准机器人连杆参数
根据阻抗控制器的参数分析,并且结合式(16)和电梯导轨校准机器人的实际控制模型,取惯性参数Md=diag[1,1],阻尼参数Kd=diag[300,1 300],刚度参数Bd=diag[0.5,0.5],环境刚度Ke=diag[10 000,100 000] N/m。
设定机器人末端执行器的笛卡尔初始坐标为[x,y,z] = [0.81,0,0.242],导轨的坐标为[x,y,z] = [0.7,0.025 8,0.242],导轨校准终止坐标为[x,y,z] = [0.682,0.03,0.242],单位为m,在笛卡尔空间中进行轨迹规划。并且结合实际情况考虑机器人末端执行器校准导轨时,导轨会在x方向和y方向上受到导轨支架的限制,所以既需要防止因导轨支架对受力过大,固定导轨的支架出现断裂、导轨产生弹塑性形变而损坏导轨等安全问题,又需要稳定地控制导轨校准力,防止校准力波动过大导致机器人的晃动影响校准精度,所以在导轨的x和y方向进行力控,机器人末端的接触力由式(13)产生,末端期望接触力由式(18)产生,并模拟机器人校准电梯导轨时的运动轨迹。
仿真步长为变步长,总时长为10 s,机器人在自由空间中运动8.6 s接触到导轨后,开始调整导轨。如图5和图6所示,通过对比NormalPD、FuzzyPD和PsoFuzzyPD可以发现,采用本文方法时,机器人末端的导轨校准力和机器人末端x和y方向的位移控制更为平滑,无波动,超调更小,进入稳态的时间更快,震荡次数更少,从而使得导轨调节时间更短,可以防止在实际调整过程中出现的安全问题,并且可以精确地控制调整精度。

图5 导轨校准力变化曲线
如图7所示,模拟仿真的机器人关节误差采样周期取0.002 s,并在机器人的运动规划过程中得到各关节的轨迹跟踪偏差,在8.6 s接触到导轨后,关节误差波动明显,3种控制器均可快速调节误差,表现有不错的快速响应性,通过对比NormalPD、FuzzyPD和PsoFuzzyPD可以发现,本文设计的力位控制器利用PsoFuzzyPD对PD的2个参数进行自动寻优和自调整,相比于NormalPD和FuzzyPD在轨迹跟踪偏差上有最小的上升时间和最小的超调量。进一步采用式(7)可计算得到机器人末端关节在关节空间中的目标函数值如表2所示,并用该值表征机器人末端关节的仿真轨迹与期望轨迹的偏差[11],可见采用PsoFuzzyPD的控制器具有更小的轨迹跟踪误差,在笛卡尔空间中轨迹跟踪偏差分别比FuzzyPD控制器和NormalPD控制器小42.92%和47.39%。

图6 机器人末端夹持器x和y方向位移
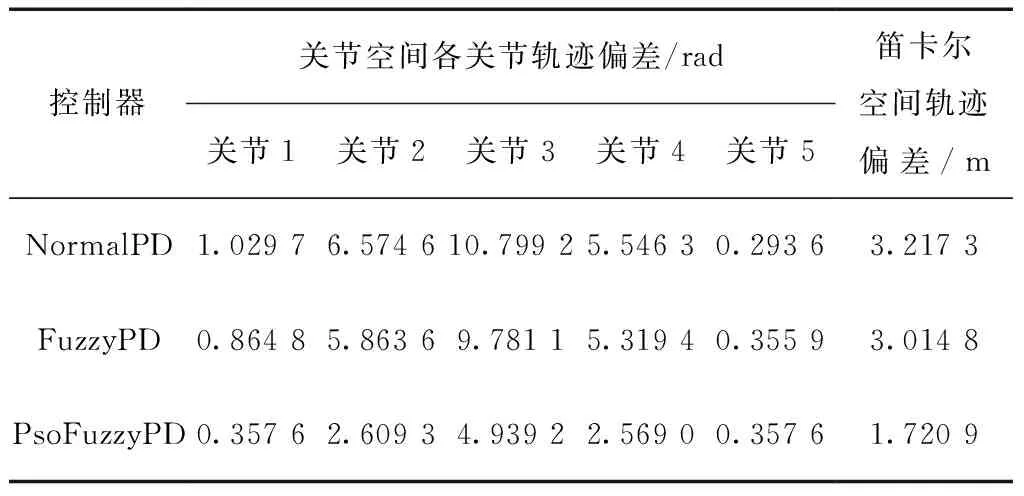
表2 轨迹偏差
仿真结果表明,采用本文方法进行仿真时,末端执行器实际终止坐标为[x,y,z] = [0.682 2,0.029 5,0.242 0],单位为m,在x方向上有0.2 mm的位置误差,在y方向上有0.5 mm的位置误差,符合位置控制精度要求。并且校准力控制平滑,无波动,在x方向上最终稳定在178.33 N,在y方向上最终稳定在373.59 N,均未超过最大校准力限制。

图7 关节空间轨迹跟踪偏差
5 结束语
针对电梯导轨校准机器人的位置/力控制问题,本文提出了一种基于改进粒子群算法和模糊PD的电梯导轨校准机器人力位控制方法,通过该控制方法可使电梯导轨垂直度的重复调整精度达到±0.5 mm,提高电梯导轨校准力的控制精度和稳定性。首先建立了电梯导轨校准机器人的整体控制框架,之后设计了改进的粒子群优化模糊PD+前馈控制器作为机器人的位置控制器,可以自适应不同的接触环境和工作条件,自动改变PD控制器的参数,提高位置控制精度,最后设计了阻抗控制外环,对末端期望力进行自适应调整,实现平滑稳定的校准力控制。通过现场实际使用反馈,该控制系统运行稳定、实用性强、满足用户对导轨垂直度精确调整和校准力大小控制稳定的使用需求,具有一定的应用推广价值。

