论如何培养初中学生的数学核心素养——以“一元一次方程”的教学为例

苏州太湖国家旅游度假区香山中学 徐 萍

1 数学核心素养的本质

义务教育数学新课程标准中提出了数据分析观念、运算能力、模型思想等十个有关核心素养，这些素养是教师在教学实践中应当培养学生的有关数学的思维、感悟和能力等的着重点，更是打造新世纪高素质人才的重点.因此，将这些核心素养的培养作为初中数学课堂上的教学目标，是当前教学的重中之重.

2 数学课堂中培养学生核心素养的思路

要想在初中数学课堂中实现培养学生核心素养这一教学目标，教师的教学体系和教学思路应该完整且具备一定的目的性.不管是课前先导教学、课下的习题演练，抑或是课后的教学反思，内容都应该丰富，且教学环节应该紧密.教学设计要遵循由浅到深这一基本原则.下面笔者以“一元一次方程”这一章的教学为例，谈一谈如何在课堂教学中培养初中生的核心素养.

2.1 从“从算式到方程”出发，增强数据分析能力

数据分析能力是指学生对于数据的认识、收集、整理、表述以及探究能力的集合.在教学课堂上培养学生的数据分析能力，有助于学生认识现实生活中的数据，并通过自己的感知收集和整理数据，是帮助学生将数学联系到生活实际中的关键点.在初中数学的学习阶段，教师应该认识到对学生的数据分析素养的培养不应该只停留在对数据的整理而应该着重于对数据的探究以及发现隐藏的数据关系上.而“从算式到方程”这一小节的内容，则是教师引导学生开始探究数据的最好落脚点.

“从算式到方程”这节课的教学，以一道常见的应用题导入.

例1春季来临，某商场对原来每件进价为200元的一批冬装进行打折促销活动，以减少库存，利于春装销售，决定将这批冬装按标价打六折销售，打折后每件服装还能获利20%，则该冬装每件的标价是多少元？

分析：这是一道常见的应用题.设该冬装每件的标价是x元，用x表示出六折出售价，每件冬装的进价乘20%求出单件利润，再由六折出售价减去进价等于所获利润，进而列方程求解.

解：设该冬装每件的标价是x元，根据题意列出一元一次方程0.6x-200=200×20%，解得x=400.

所以该冬装每件的标价是400元.

设计意图：本小节教学先以一个常见的应用题导入，让学生了解什么是未知数、方程、一元一次方程，以及方程的解.再通过分析解题思路，帮助学生学会将实际问题转化为数学问题，学会用未知数以及方程将数量关系符号化并能挖掘出隐含的数据关系，进而开展数据探究活动.本小节内容作为小学与初中数学的衔接知识点，应该着重培养学生对概念认识以及挖掘数据、发现问题的能力，为后续解决复杂型应用题、条件隐含型应用题夯实基础.

2.2 从“解一元一次方程”出发，增强运算能力

运算能力是指能够依据法则和运算规律正确开展运算的能力.培养运算能力要求学生能理解运算规律和法则并能用简洁的运算来解决问题.运算能力的形成分为两个阶段：其一是能够按照一定的程序和步骤进行正确运算，这要求学生熟悉运算过程；其二是要求学生能根据题目条件和特殊情境，寻找合理以及简洁的运算途径和方式.在初中数学学习阶段，一元一次方程的解法即是通过移项和合并同类项来化简方程进而求解，其实求解的过程是对学生运算能力的综合考量.因此，对学生运算能力的培养不仅要求学生能正确求解方程，更要能做到简洁快速.

下面以两道较复杂的含分数的一元一次方程为例.

分析：这是一道含有分数的较复杂的一元一次方程，在求解此类方程时，要遵循解一元一次方程的思路——去分母、去括号、移项、合并同类项、系数化为1，根据步骤求解.

解:去分母，得2x-6-5x+20=-1.

移项合并同类项，得-3x=-15.

系数化为1，解得x=5.

例3关于x的方程3x-mx=3m-3的解是方程3x+1=2x+2的解的3倍，求m的值.

分析：分别求方程3x-mx=3m-3和3x+1=2x+2的解，再由题意列出关于m的方程，通过解方程即可求出m的值.

解方程3x+1=2x+2，得x=1.

设计意图：本小节内容主要是讲授一元一次方程的解法和基本步骤，让学生学会从去分母、去括号到移项、合并同类项再到系数化为1，最后求得方程的解.这一章节对学生的运算能力要求较高，也是教师注重培养学生运算能力的关键章节.因此在教学前期教师应着重于教学步骤和教学思路的搭建，让学生切记不可为了追求快速解题而省略步骤，只有将每个步骤的基础打牢，积累经验，学生才能在后续的运用中做到简洁且快速地解题.

2.3 从“实际问题与一元一次方程”出发，培养模型思想

模型思想指的就是学生在数学中建立模型的思想，而使用数学语言描述的数学结构就称为数学模型，数学建模属于一门应用数学.它要求学生学会如何将实际问题通过分析、整理演变成一个数学问题，然后用合适的数学方法解决.建立模型的过程必须准确、合理且适用，只有模型与实际情况吻合，计算结果才有实际意义.在初中数学学习阶段，实际问题是数学建模思想最广泛的表现领域，它不仅要求学生能灵活分析题目中的条件，准确抓取数据信息，还要求学生有搭建模型的能力.在“实际问题与一元一次方程”这个章节的学习中，教师要着重培养学生搭建数学模型的能力，为后续学习复杂型应用题做好基础准备.

下面以常出现在应用题中的“工程问题”为例.

例4一项工程，甲单独做a天完成，乙单独做b天完成.

(1)甲的工作效率为，乙的工作效率为;

(2)若甲先单独工作6天后，甲、乙又合作2天完成了这项工程，则可以列出的等式为；

(3)若甲、乙合作n天完成了整个工程的一半，则可列等式为；

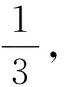
分析：第(1)问用工程总量1除以甲单独做完成的天数，即为甲的工作效率，同理可求乙的工作效率；第(2)～(4)小问均可根据等量关系列出方程即可.

设计意图：“工程问题”是一类较典型的应用问题，需要学生搭建模型，而搭建模型的依据是工程量=工作效率×工作时间.在解决工程问题时，等量关系都是从以上三个量中找.在实际解答过程中，我们通常将工程量看作整体“1”，以保证在仅知道工作效率或是仅知道工作时间的条件下，仍然能表示出剩下的单位.这就是搭建“工程问题”模型的基本思路.教师在讲解“实际问题与一元一次方程”这一小节的内容时，除了要培养学生分析条件、整理数据的能力之外，还要帮助学生学会搭建各种数学模型，比如“利润问题”“浓度问题”“行程问题”“利息问题”等，让学生在解题过程中学会举一反三，并能将这一思维延续到后续的数学学习过程中.

3 总结

数学学习是一个缓慢且长期的过程，教师需要在每节课的教学中不断渗透对学生核心素养的培养，让学生在学习中能感知到数学的魅力，从而更好地掌握数学知识，并能将课堂上所学习到的知识灵活应用到实际生活中去解决实际问题，让学生真正领会到数学学习的快乐.