一道两线段长乘积为定值月考题的背景与性质应用

北京市第十二中学高中部(100071) 刘刚

1.试题呈现

(1)求椭圆C的方程及A点坐标;

(2) 设直线l与x轴交于点B,过点B的直线与椭圆C交于E,F两点,记A在x轴上的投影为G,T为BG的中点,直线AE,AF与x轴分别交于M,N两点,试探究|TM|·|TN|是否为定值,若为定值,求出此定值;否则,请说明理由.

试题考查了椭圆的标准方程、几何性质、直线与椭圆的位置关系以及定值问题,考查了方程、转化与化归等数学思想以及坐标法的应用,检验了数学运算、逻辑推理等数学核心素养.试题平中见奇,内涵丰富,符合新课标理念.

2.试题解答

3.试题背景

为了揭示题1 的背景,下面先给出高等几何中的几个定义和性质.

(1)调和点列与调和线束

定义1一条直线上的四个点A,B,C,D如果满足,那么称A,B,C,D为调和点列,亦称B,D调和分割线段AC.过调和点列A,B,C,D所在直线外一点P,向A,B,C,D引四条线束,称这四条线束PA,PB,PC,PD为调和线束.

性质1如图1,设直线l与调和线束PA,PB,PC,PD分别交于点A′,B′,C′,D′,则A′,B′,C′,D′为调和点列.

图1

性质2如图2,如果PA,PB,PC,PD为调和线束,且PD//AC,则PB平分线段AC.

图2

(2)极点与极线

定义2如图3,若点P不在圆锥曲线Γ 上,过点P引两条割线与Γ 依次交于E,F,G,H四点,直线EH与FG交于点M,直线EG与FH交于点N,则直线MN为点P关于Γ 的极线,直线PM为点N关于Γ 的极线,直线PN为点M关于Γ 的极线.若点P在圆锥曲线Γ 上,则过点P的切线即为极线.

图3

定义3已知有心圆锥曲线Γ:ax2+by2=1 (ab/=0),极点P(x0,y0),则点P关于圆锥曲线Γ 的极线方程为ax0x+by0y=1,当y0=0 时,极线方程为ax0x=1.

若圆锥曲线Γ 是抛物线y2=2px(p ＞0),极点P(x0,y0),则点P关于圆锥曲线Γ 的极线方程为y0y=p(x+x0),当y0=0 时,极线方程为x0+x=0.

性质3如图4,已知点P是圆锥曲线Γ 外一点,点P关于Γ 的极线AB与Γ 相交于A,B两点,则PA、PB是Γ 的两条切线;过点P的一条割线交Γ 及极线AB于点M,N,Q,则P,M,Q,N为调和点列.

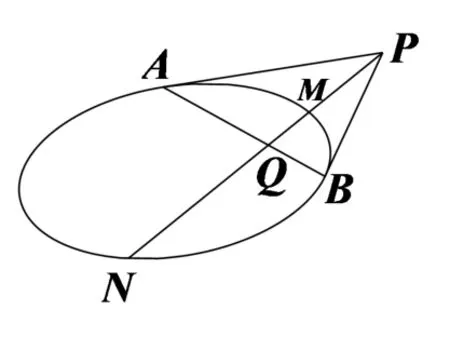
图4

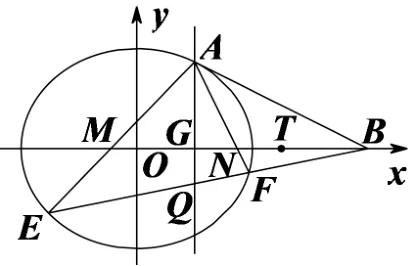
图5

本题经过推广,还可以得到更一般的结论.

定理如图6,已知椭圆C:=1 (a ＞b ＞0),点B是椭圆C外一点,过点B作椭圆C的两条切线PA、PD,其中A、D是切点,直线OB与直线AD交于点G,T为BG的中点,过点B的直线与椭圆C交于E,F两点,直线AE,AF与直线OB分别交于M,N两点,则|TM|·|TN|为定值|TG|2.

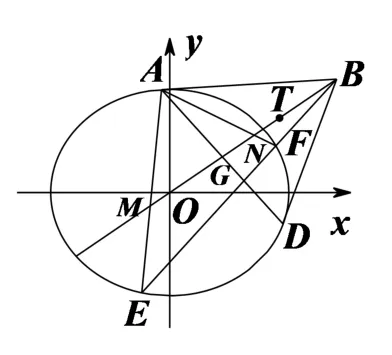
图6

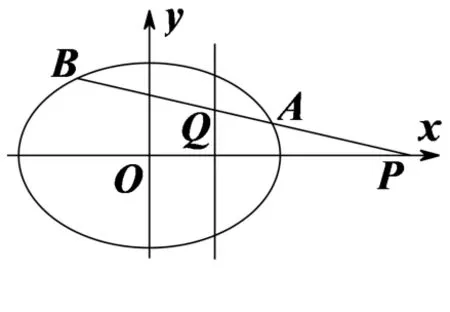
图7

4.性质应用

简解(1)椭圆C的方程为=1.

(2)如图8,连接AB,设l与直线x=-2 交于点D,因为B(-4,0),所以点B关于椭圆C的极线方程是x=-2,于是点B,M,D,N是调和点列,即AB,AM,AD,AN是调和线束.因为PQ//AD,所以AB平分线段PQ,故

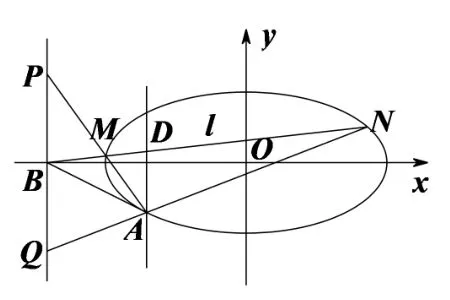
图8

题目4(2018 年高考北京卷理科第19 题)已知抛物线C:y2=2px经过点P(1,2),过点Q(0,1)的直线l与抛物线C有两个不同的交点A,B,且直线PA交y轴于M,直线PB交y轴于N.

(1) 求直线l的斜率的取值范围;(2) 设O为原点,为定值.

简解(1) 略,直线l的斜率的取值范围是(-∞,-3)∪(-3,0)∪(0,1).

(2) 如图9,连接PQ,OP,设l与OP交于点D,不妨设M在线段OQ上,N在线段OQ的延长线上,即λ ＞0,µ ＜0.由已知可得直线PQ的方程为y=x+1,与抛物线C的方程y2=4x联立,得x2-2x+1=0,此时Δ=0,所以直线PQ是抛物线C的切线,P是切点.又y轴也是抛物线C的切线,O是切点,所以点Q关于抛物线C的极线是OP,所以Q,A,D,B是调和点列,于是PQ,PA,PD,PB是调和线束,由此得Q,M,O,N是调和点列,所以,即,整理得=2,即为定值.

图9