一道测试题的解法剖析

浙江省宁波市第四中学(315016) 董亚

一、试题呈现

题目(广东省2022 届高三数学综合能力测试(二))已知函数f(x)=4x3+ax+b,当x ∈[-1,1]时,|f(x)|≤1 恒成立,则a+b=____.

这是以初等函数为载体,通过数形结合、分类讨论等数学思想来解决最值、单调性、不等式恒成立问题,试题以三次函数形式出现,新颖独特,有着深刻的数学背景,本文将全方位对这个问题进行剖析.

二、解法剖析

1.特值探求法

由当x ∈[-1,1]时,|f(x)|≤1 恒成立,得:

2.图象探求法

作出函数g(x)=-4x3+1 的图象,与直线x=1交于点A(1,-3),过点A作函数y=g(x) 图象的切线 (如图1),其方程为y=-3x.由于h(x)=-4x3-1 与g(x)=-4x3+1 的图象关于原点对称,故直线y=-3x.也过点(-1,3),且与函数y=g(x) 图象相切,故当a=-3,b=0 时,恒成立,即a+b=-3.

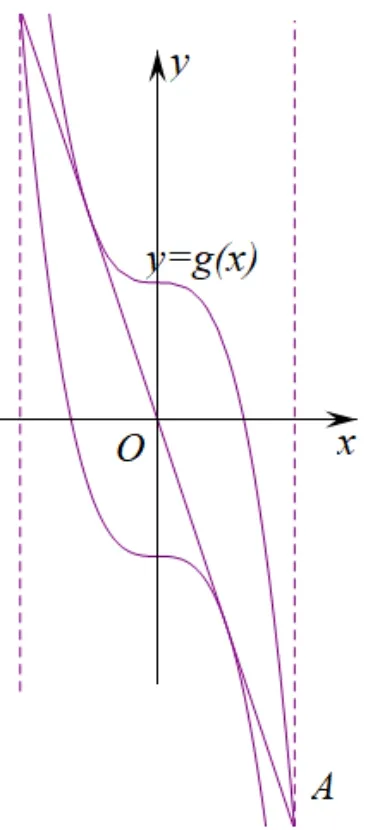
图1

3.最值探求法

4.模型探求法

令x=cosα ∈[-1,1],联系三倍角的余弦公式cos 3α=4cos3α-3 cosα.故f(x)=4cos3α-3 cosα+(a+3)cosα+b=cos 3α+(a+3)cosα+b,注意到|cos 3α|≤1恒成立,只须(a+3)cosα+b恒为零,即a=-3,b=0.所以a+b=-3.

评析这类题就是大家熟知的切比雪夫的最佳逼近问题,在以往试题中多是以二次函数形式出现,对于三次函数来说,还可借用三角函数模型:cos 3α=4cos3α-3 cosα,sin 3α=3 sinα-4sin3α.

三、相关问题

例1(2008 年高考江苏卷)f(x)=ax3-3x+1 对于x ∈[-1,1]时,总有f(x)≥0 成立,求实数a的值.

三、相关结论

定理设实系数三次函数f(x)=ax3+bx2+cx+d,当x ∈[-1,1]时,|f(x)|≤1 恒成立,则|a|+|b|+|c|+|d|≤7.

证明由于|f(±x)|≤1,不妨设a ＞0,b≥0.