基于广义梯形模糊数的基本概率指派方法
宋香鹏,肖建于,吴克凤,伏明兰
(淮北师范大学 计算机科学与技术学院,安徽 淮北 235000)
D-S证据理论[1]中基本概率指派(Basic Probability Assignment,BPA)是应用D-S证据理论识别框架(Frame of Discernment,FOD)的核心和关键。其中BPA的构造与确定并没有一个固定的模式,需要考虑不同应用背景下的复杂条件,这是制约证据理论应用推广的首要原因[2-3]。国内外众多学者对此问题进行了研究,并且也提出了不同的解决方案。Deng和Wang[4]提出在信任区间上使用多子集焦点元素的BPA转换方法;Zhang和Deng[5]提出了根据属性值构造的三角模糊数来指派BPA;Fan等[6]提出利用基于三角模糊数的K-means++算法构造BPA;Qin和Xiao[7]使用测试样本与模型间的相似度来进行基本概率赋值。
文献[4-7]主要思想是通过利用模糊数对不同目标类的各种属性进行建模,然后根据模糊数的隶属度得到各个焦元的信任度,最终进行归一化处理,计算出满足条件的BPA。其中三角模糊数在处理BPA的构造具有很高的应用性,但是当处理区分度较小的数据时,容易引起焦元“爆炸”(即焦元呈指数级数增长)。本文利用机器学习中的鸢尾花数据集,以广义梯形模糊数为基础,建立了单元素命题和多元素命题的表示模型,并计算出模糊数的隶属度来构造BPA。此构造方法相对简捷,有效减少了焦元增加问题,对各类数据有更强的适用性,为证据理论在目标识别和变压器故障诊断等工业应用中提供了理论依据。
1 广义模糊数的构造
1.1 广义模糊数的定义
论域U到[0,1]上任意映射,确定U上的广义梯形模糊数为A=(a,b,c,d;w),对应的隶属度函数为[8]:
(1)
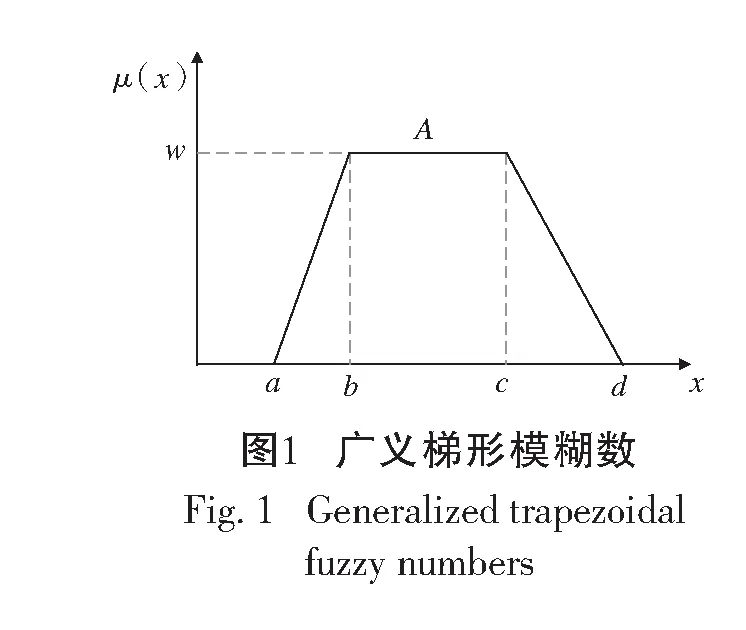
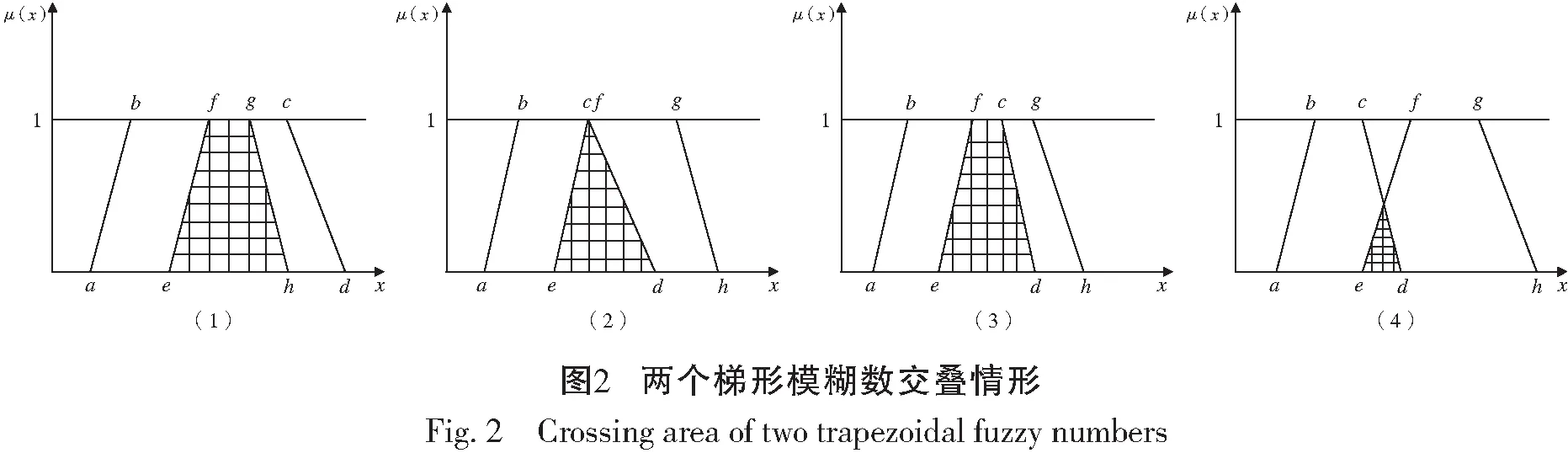
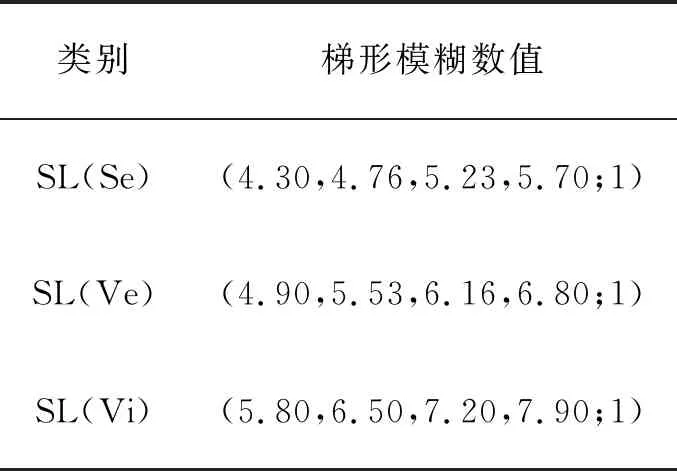
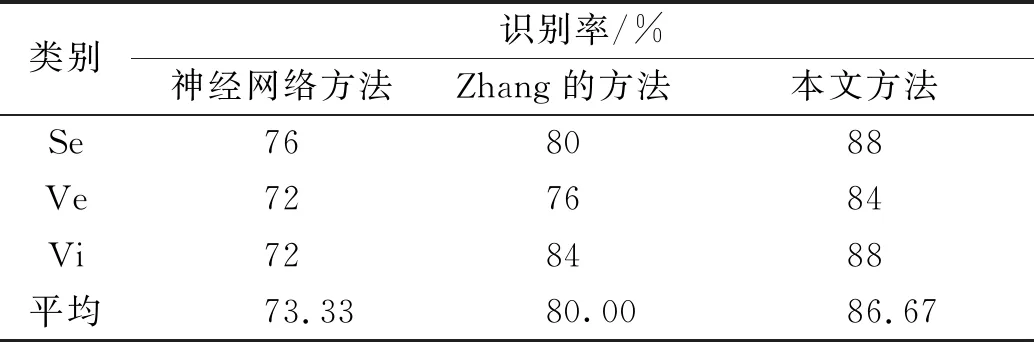
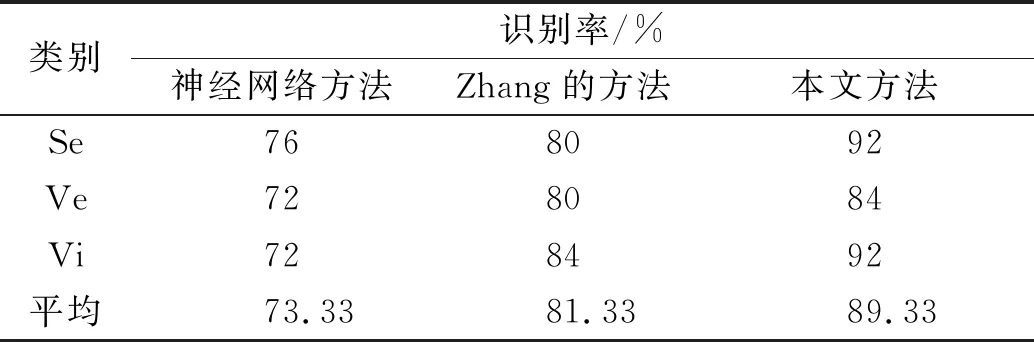
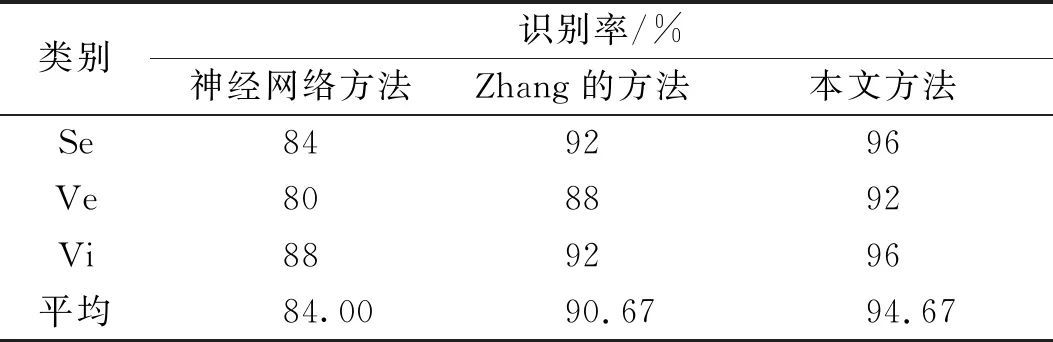
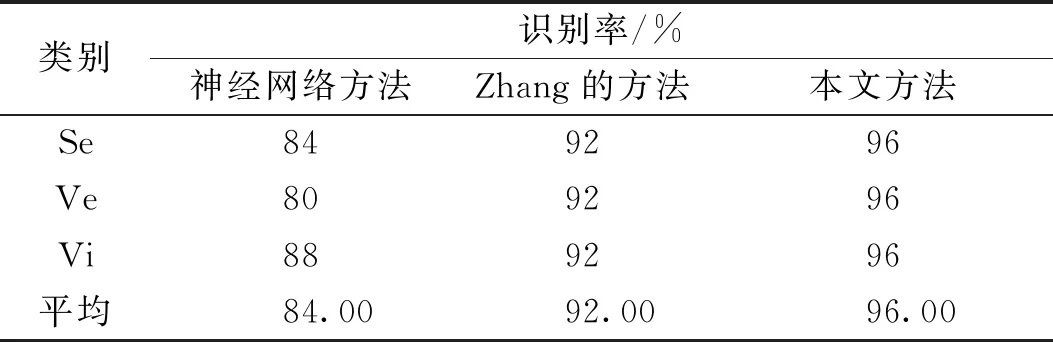
其中-∞ 针对目标识别问题,可以利用已有的历史数据集获得其中某指标的最大值和最小值,并且求得其中的三等分均值。基于这三等分均值可以构造出一个梯形模糊数来描述命题。假设某识别问题的FOD为Θ={θ1,θ2,…θi,…,θn},且Θ中的每个元素都是互斥的。系统中用S表示传感器,即传感器收集的识别类别的第m个指标为Sm;系统需要识别的目标可表示为p(p∈θi,i=1,…,n);属于θi类的样本为Hik,Tm(Hik)为传感器Sm对此样本的度量向量。构造梯形模糊数表示模型的具体步骤如下: Step 1:确定度量向量。 针对每个类别θi,各传感器Sm对于某类别θi的训练样本Hik的度量向量为 Step 2:计算梯形模糊数值。 假设类别θi有Zm个训练样本,其中属于指标m的梯形模糊数值为: (2) (4) (3) (5) Step 3:梯形模糊数交集分析。 Step 4:确定广义模糊数。 梯形模糊数的交集部分可能为梯形或三角形,根据实际情况确定隶属度w,称此类模糊数为广义梯形模糊数或是广义三角模糊数。 2)若测量值并未出现在初始梯形模糊数表示模型范围中,则有两种处理方式:①当系统属于开放世界假设情况下,说明此测量值属于未知的类别,处理方法则是将BPA全部指派给空集∅,即表示为m(∅)=1。②当系统属于封闭世界假设情况下,说明训练集选择可能不完善,处理方法则是将BPA全部指派给全集Θ,即表示为m(Θ)=1。但是在实际工程应用中,一般在确定此数据类型后,然后将其加入到训练集中,重新修正并确定相应类别的梯形模糊数。 3)依次计算出各命题的隶属度之后,可通过以下方法进行BPA的指派:首先用1减去最大隶属度,然后赋值给全集Θ,即认为此部分的信息属于未知空间。为计算方便以及保证BPA之和为1,将计算出的隶属度进行归一化处理。具体公式如下: (6) (7) (9) (8) (10) 其中p,q,z分别是梯形模糊数、交叠的梯形模糊数、三角模糊数模型的焦元个数。根据公式依次计算出各属性的BPA指派。 4)某一证据对某属性的基本概率分配为0,会导致最终合成的mass函数结果为0,即使其他证据对该事件分配的概率较高或增加新证据表明该事件有较大概率也无法影响合成结果[10-11]。为避免冲突证据影响合成结果不准确,故使用以下合成方法:m1,m2,…,mn所对应的证据集为F1,F2,…,Fn,并设证据集i和j之间的冲突大小为kij,则 (11) m(Θ)=0, m(A)=p(A)+k·ε·q(A),A≠∅,X, (12) (14) m(X)=p(X)+k·ε·q(X)+k(1-ε), (13) (15) 鸢尾花数据集(Iris data)共有150个样本数据,包含3个类别,分别是Setosa(Se)、Versicolour(Ve)和Virginica(Vi),每个类别各有50个实例样本。并且Iris数据集还提供4个属性:萼片长度(SL)、萼片宽度(SW)、花瓣长度(PL)、花瓣宽度(PW)。在以下实验中,每个属性都被认为是独立的传感信息源,每类各随机抽取25个实例样本数据,剩下的25个实例样本数据作为测试样本[12]。 本实验中,根据随机抽取的样本数据得到鸢尾花萼片长度的梯形模糊数值如表1所示,图3给出了鸢尾花4个属性的梯形模糊数表示模型,表2则是3类鸢尾花交叠部分为三角形的三角模糊数值。 表1 萼片长度的梯形模糊数值 表2 3类鸢尾花交叠部分的广义模糊数 假设由传感器系统测得一个鸢尾花的样本值为(4.70、3.20、1.60、0.20 cm),对于此花的萼片长度4.70 cm,利用本文的BPA指派方法,得到的BPA如下: m(Se)=0.8696,m(Θ)=0.1304, 此样本的4个属性指派的BPA如表3所示。 为避免冲突证据的影响,使用公式(11)—(15)进行证据间的合成。其合成结果为: m(Se)=0.7860,m(Se,Vi)=0.0521,m(Θ)=0.1619。 最后根据决策支持系统中,BPA最大的种类即为样本所属类别,故此样本属于Se。 表3 某样本生成的BPA 采取封闭世界假设实验[13],即认为样本数据集是完全的,在本实验中则是确定数据集中具有Se、Ve和Vi的类别数据。将利用神经网络方法[14],Zhang的三角模糊数方法[5]和本文的BPA指派方法进行对比实验。实验数据同上,数据中50%作为训练集,剩下50%作为测试集。实验结果如表4和表5所示: 表4 有噪声环境下完全FOD的不同方法识别率 表5 无噪声环境下完全FOD的不同方法识别率 在本节中,使用Iris数据集所有类别来建立目标模型,即识别框架是完全的,测试实例也是已知的。主要区别是有无噪声环境,即训练数据集中是否含有每个类别的最大值与最小值,若无最大值或最小值,则认为是噪声环境,反之则认为是无噪声环境。从表4和表5中的实验结果可以得出:在完全FOD下使用神经网络方法进行识别分类,在有无噪声环境情况下,平均识别率都为73.3%,这是因为训练数据过少,导致神经网络的学习并不完善,从而影响到识别率较低。Zhang使用的三角模糊数交叉区域识别方法在噪声环境下的平均识别率为80.00%,无噪声环境下平均识别率为81.33%,相比于神经网络方法,识别率显著提高。但与本文改进的方法相比,由于其焦元的增加,识别率并没有本文的方法表现优良。本文利用梯形模糊数模型的方法在有无噪声环境下的平均识别率分别达到86.67%和89.33%。 在开放世界假设实验下[15-16],将Se类和Ve类视为已知类,Vi类为未知类,其他的参数与之前实验相同。通过Se类和Ve类训练出的梯形模糊数模型分别识别测试样本中的Se类和Ve类,同时根据此模型识别未知类Vi。实验结果如表6和表7所示: 表6 有噪声环境下不完全FOD的不同方法识别率 表7 无噪声环境下不完全FOD的不同方法识别率 通过对比实验发现,在不完全的识别框架下,噪声环境是否存在对识别率的影响并不是很大,由于整体的未知量增加,对已知类判断更加准确。其中本文的改进方法效果最好,在无噪声环境下,对各类别的识别率均达到了96.00%。其根本原因是利用梯形模糊数的模型有效减少了焦元的生成量,可以更加准确地完成BPA的指派,由此说明改进的方法在实际分类中应用有效。 本文利用广义梯形模糊数模型中的隶属度进行证据理论中的基本概率指派,解决了证据理论在应用中的关键性问题。通过在经典的鸢尾花数据集上的对比实验,证明了本文提出的方法在目标分类应用中是有效的,并且此方法在处理小规模数据集时有着独特的优势,在实际工程应用中,只要有一定的数据,均能使用此方法进行基本概率的指派。与其他方法相比,此方法生成的焦元更少,可以更准确地得到量化指标,较好地解决了评价体系中的主观性问题。实验结果也证明,此方法在开放世界和封闭世界中都可以很好地进行识别。由于利用基本概率赋值函数的形式构造BPA可以有效处理各类基础信息,在未来研究中可以将此方法应用在多源信息融合领域中。1.2 广义模糊数的构造
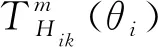
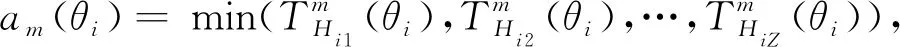
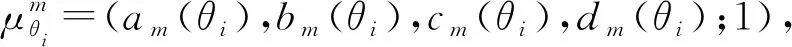
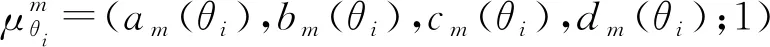
2 基于广义梯形模糊数的BPA指派
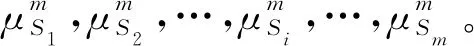
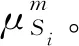
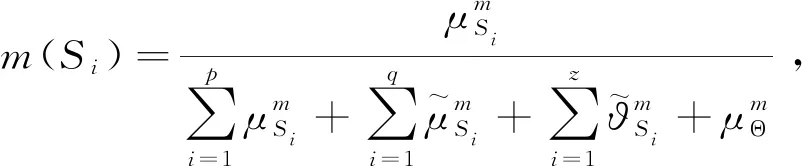
3 目标识别实验
3.1 基本识别实验


3.2 封闭世界假设模拟实验
3.3 开放世界假设模拟实验
4 结 论

