从一个四维左对称代数构造一些八维相空间
侯冬平,丁梦菲
(云南师范大学 数学学院,昆明 650500)
李代数与约当代数、交错代数被并称为三类非常重要的非结合代数。19世纪后期,挪威数学家S.Lie在研究连续变换群时引进了李代数。李代数与李群有密切的关系,之后作为一门独立的学科迅速发展,并且广泛应用于数学及物理的许多领域。
如果一个李代数上存在一个非退化的反对称的辛形式,则称这样的李代数为辛李代数[1-3]。在辛李代数上存在一种新的代数结构,称之为左对称代数(也称为预李代数),是一类非常重要的非结合代数[4]。左对称代数与很多数学学科和数学物理的许多领域都有密切的关系,如仿射流形[5]、李群上的仿射结构[6]、李代数[7]等。通过一个左对称代数上的S-方程的一个对称解,可以构造出一个特殊的辛李代数(也称为相空间)。文献[8]中给出了一些四维和六维的相空间,然而,对于更高维数的相空间人们还知之甚少。
文献[9]给出了一类特殊的n维左对称代数An(域的直和),设e1,e2,…,en是An的一组基,则:eiej=δijei,1≤i,j≤n。当n<4时,An上的S-方程的对称解及其对应的相空间都已经通过直接计算得到。本文主要给出A4上的S-方程的所有对称解及其对应的相空间,其中
矩阵中(i,j)元为ei,ej的乘积。
1 基本概念
定义1[4,10]设g是数域F上的一个线性空间,在g中定义双线性乘法[,]满足下列条件:
[x,x]=0;[[x,y],z]+[[y,z],x]+[[z,x],y]=0,∀x,y,z∈g,
(1)
则称g是数域F上的一个李代数。
定义2[4]设g是数域F上的一个李代数,V是数域F上的一个线性空间,若g到gl(V)线性映射f满足等式:
f([x,y])=f(x)f(y)-f(y)f(x),∀x,y∈g,
(2)
则称f是李代数g的一个以V为表示空间的线性表示,记为(f,V)或f。如:
ad:g→gl(g),xadx,∀x∈g,adx(y)=[x,y],∀y∈g,
称为g的伴随表示。
定义3[4,10]设A是数域F的一个线性空间,在A中定义双线性乘法“·”满足等式:
(x·y)·z-x·(y·z)=(y·x)·z-y·(x·z),∀x,y,z∈A,
(3)
则称A是一个左对称代数或预李代数。此时,定义乘法“[,]”:
[x,y]=x·y-y·x,∀x,y∈A,
(4)
则(A,[,])是一个李代数,称为左对称代数A的邻接李代数,记为G(A)。
定义4[4]设V是数域F上的一个线性空间,V*是V的对偶空间,则存在一个自然的非退化对称的V*×V到F的双线性映射“〈,〉”满足:
〈v,a*〉=〈a*,v〉=a*(v),∀a*∈V*,v∈V。
(5)
性质1[4]设(A,·)是一个左对称代数,G(A)是它的邻接李代数,则:
1)线性映射:
L.∶G(A)→gl(A),xL.(x),∀x∈A,其中L.(x)(y)=x·y,∀y∈A,
是李代数G(A)的一个表示,称为G(A)的正则表示。
2)线性映射:
L.*∶G(A)→gl(A*),xL.*(x),∀x∈A,
〈L.*(x)(a*),y〉=-〈a*,x·y〉,∀x,y∈A,a*∈A*,
(6)
是李代数G(A)一个表示,称为G(A)的正则表示的对偶表示。
定义5[4]设g是一个李代数,g上的非退化的反对称双线性型f,如果满足:
f([x,y],z)+f([y,z],x)+f([z,x],y)=0,x,y,z∈A,
(7)
则称f是g上的一个辛形式。具有辛形式的李代数称为辛李代数。
性质2[4]设g是一个李代数,f是g上的辛形式,则在g上存在一个相容的左对称代数结构“·”如下:
f(x·y,z)=-f(y,[x,z]),x,y,z∈A。
(8)
定义6[8]称李代数T(g)是一个相空间,若以下条件成立:
1)作为线性空间,T(g)是g与g*的直和,且g与g*是T(g)的子代数;
2)反对称双线性型:
fp(x+a*,y+b*)=-〈x,b*〉+〈a*,y〉,∀x,y∈g,a*,b*∈g*
(9)
是T(g)上的辛形式。
定义7[8]设(A,·)一个左对称代数,r是A与A的张量空间里的一个元素,称方程:
-r12·r13+r12·r23+[r13,r23]=0
(10)
为(A,·)上的S-方程。其中符号如下:
(11)
(12)
(13)
引理1[8]设(A,·)是一个左对称代数,r是A上的S-方程的一个对称解,则r可以被看作A*到A的一个线性映射:
〈r(a*),b*〉=〈r,a*⊗b*〉,∀a*,b*∈A*。
(14)
从而r可以诱导出A*的一个左对称代数结构“·”相空间T(G(A)),且T(G(A))上的左对称代数结构“*”和李代数结构如下:
a**b*=a*·b*=-r.*(r(b*))a*+ad*(r(a*))b*,∀a*,b*∈A*;
(15)
[a*,b*]=L.*(r(a*))b*-L.*(r(b*))a*,∀a*,b*∈A*;
(16)
x*a*=x·r(a*)-r(ad*(x)a*)+ad*(x)a*,∀x∈A,a*∈A*;
(17)
a**x=r(a*)·x+r(R.*(x)a*)-R.*(x)a*,∀x∈A,a*∈A*;
(18)
[x,a*]=[x,r(a*)]-r(L.*(x)a*)+L.*(x)a*,∀x∈A,a*∈A*。
(19)
2 四维左对称代数A4上的S-方程的对称解和其对应的相空间
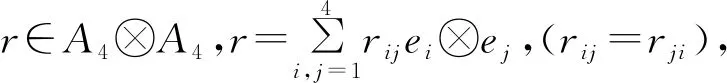
r12(r12-r11)=r12(r22-r12)=r12(r23-r13)=r12(r24-r14)=0;
r13(r13-r11)=r13(r23-r12)=r13(r33-r13)=r13(r34-r14)=0;
r14(r14-r11)=r14(r24-r12)=r14(r34-r13)=r14(r44-r14)=0;
r23(r13-r12)=r23(r23-r22)=r23(r33-r23)=r23(r34-r24)=0;
r24(r14-r12)=r24(r24-r22)=r24(r34-r23)=r24(r44-r24)=0;
r34(r14-r13)=r34(r24-r23)=r34(r34-r33)=r34(r44-r34)=0。
证明根据定义7,由于A4交换,直接计算可以得到
-r12·r13+r12·r23+[r13,r23]=-r12·r13+r12·r23
由于向量组ei⊗ej⊗ek,1≤i 定理1设e1,e2,e3,e4为左对称代数A4的一组基,e1*,e2*,e3*,e4*为其对偶基,则由A4上的S-方程的对称解r=(rij)诱导出的相空间T(G(A))上的李代数结构如下(只写出非零的括号积): 证明首先证明左对称代数A4上的S-方程的对称解只有以上15种。 由命题1知道,r=(rij)是A4上的S-方程的对称解当且仅当rij是命题1中的方程组的解。 1)当r12,r13,r14都不等于0时,结合命题1中的方程可得 r11=r12=r13=r14=r22=r23=r24=r33=r34=r44≠0, 得到r=r1。 2)当r12,r13不等于0,且r14=0时,代入命题1中的方程可得: 3)当r12,r14不等于0,且r13=0时,根据命题1中的方程可得: 4)当r12不等于0,且r13=r14=0时,命题1中的方程组同解于以下方程组: 4a)当r34不等于0时,易知,r33=r44=r34,得到r=r4。 4b)当r34等于0时,得到r=r5。 5)当r12=0,且r13,r14不等于0,代入命题1中的方程可得: 6)当r12=r14=0,且r13不等于0,命题1中的方程组同解于以下方程组: 6a)当r24不等于0,易知:r22=r44=r24,解得:r=r7。 6b)当r24=0时,解得:r=r8。 7)当r12=r13=0,且r14不等于0,命题1中的方程组同解于以下方程组: 7a)当r23不等于0,得到:r22=r33=r23,解得r=r9。 7b)当r23=0时,解得r=r10。 8)当r12=r13=r14=0时,命题1中的方程组同解于以下方程组: r23(r23-r22)=r23(r33-r23)=r23(r34-r24)=0; r24(r24-r22)=r24(r34-r23)=r24(r44-r24)=0; (r24-r23)=r34(r34-r33)=r34(r44-r34)=0。 8a)当r23,r24不等于0时,得到: 8b)当r23不等于0,r24=0时,得到: 故A4上的S-方程的对称解只有以上15种。 L.*(ek)ek*=-ek*,1≤k≤4,l.*(ei)ej*=0,i≠j。 根据引理1,得到: 所以,结论(1)成立。即 同理,也可以证明其余结论成立。 本文通过一个四维的左对称代数A4上的S-方程的对称解,得到了一些非平凡的八维相空间。在一定程度上丰富了高维数相空间的例子。由于本文所用方法涉及到非线性方程组的求解,很难把这种方法推广到维数较高的代数上。因此,寻找一个比较好的解决方案是以后研究工作的一个目标。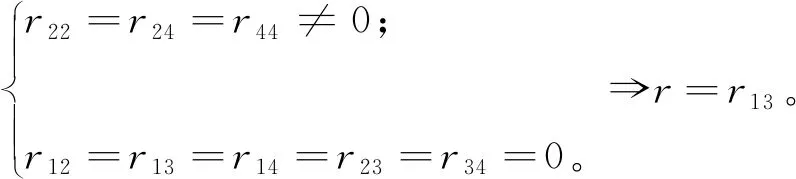

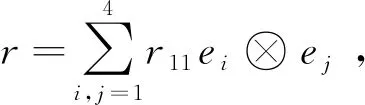

3 结 语

