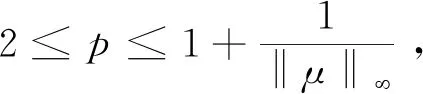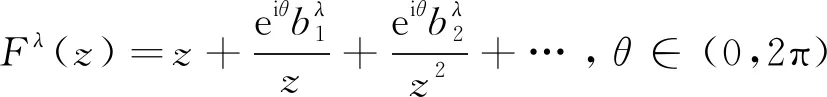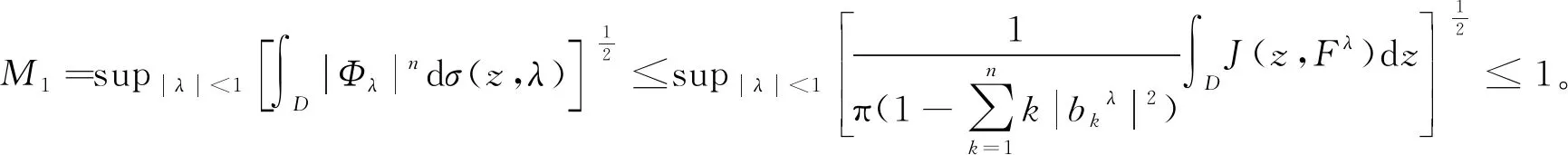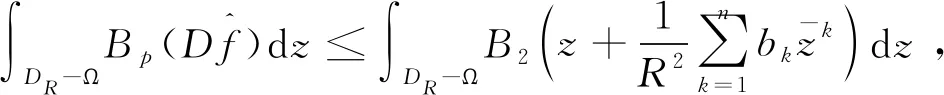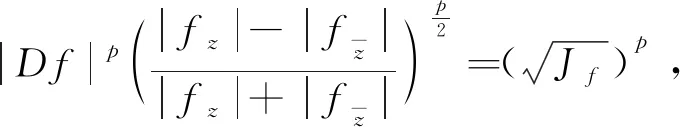一类Burkholder积分的上界及其应用
杨 敏,张 莉
(西华师范大学 a .数学与信息学院,b.公共数学学院,四川 南充 637009)
1 预备知识
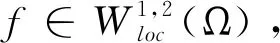
(1)
其中Beltrami系数无穷范数有界:‖μf‖∞≤k<1,则称f为k-拟共形映射。

f(z)=z+b1z-1+b2z-2+…,|z|→∞,
(2)
则称f为Beltrami方程(1)的主要解。


定义2E:n×n→是连续泛函,若对任一n),有
(3)
则称E为拟凸的。其中A表示任一线性映射(或矩阵),Ω是n上任一有界区域。
对任一固定矩阵A和任意秩为一的矩阵X,若有t→E(A+tX)是凸的,则称E是秩一凸的。相反地,如果-E是秩一凸的,则E是秩一凹的,便可以利用凹性来研究凸性。在二维中最著名的秩一凹泛函就是Burkholder泛函:
(4)
其中A是任意二阶矩阵并且|A|是A的算子范数[1-3]。
Morrey[4]指出拟凸性能推导出秩一凸,而verák[5]的研究表明在高维(维数大于2)中秩一凸不一定能推出拟凸,这就使得在二维中可能出现不同的结果[6-7]。Astala等[8]对这一问题作出了如下猜想:
猜想A秩一凸泛函E:2×2→是拟凸的。
同时,Astala等[8]根据插值引理和面积定理得到下面的定理:
定理1对于A=Id,在恒等变换的拟共形扰动下Burkholder泛函是拟凹的,当f是Ω到自身的k-拟共形映射并且在边界上是恒等时,有
(5)


2 主要引理
引理1[8](圆盘上的插值引理)令0 (6) (7) (8) 在下面定理2的条件下文献[10]得出: 本文在文献[8-10]的启发下,得到以下理论: 注意:(1)当n=0时,满足定理1的结论; (2)当n=1时,满足文献[10]中的结论。 (9) 其中τλ(z)是解析函数且满足 (10) 也就是说 (11) (12) (13) 在圆盘上的度量空间M(D,σ)上应用引理1(插值引理),其中 (14) (15) (16) 结合(14)式得到 (17) (18) 即: 定理1得证。 证明DR表示以R为半径的圆盘,由定理中R的取值情况可知Ω⊂DR,只需令定理1中 可以得到 (19) 由(19)式可得 (20) (21) 结合(20)(21)式可以得到 (22) (23) (24) 定理3得证。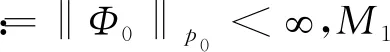

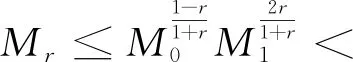


3 主要结果及其证明