负载下碳纤维布加固钢结构受弯构件理论研究
张建鹏
(1.山东省建筑科学研究院有限公司,山东 济南 250031;2.山东省建筑工程质量检验检测中心有限公司,山东 济南 250031)
0 引言
近年来,随着社会发展,我国建筑行业步入一个以既有建筑改造为主,新建建筑为辅的阶段,实际工程中,钢结构具有施工周期短,成本低,已成为被广泛应用的结构形式,但钢结构受外界条件影响较大,容易产生损伤,此时需要对结构进行加固,此类加固往往是负载条件下的加固。目前传统加固钢结构构件的方法主要包括粘钢加固、焊接加固、粘贴碳纤维等,此类加固往往在加固前首先卸载。本文主要对负载下碳纤维加固钢结构构件的理论研究,首先对粘贴碳纤维加固钢结构构件的破坏形式进行介绍,其次,由于实际工程中很容易发生端部剥离破坏,本文提出并推定出碳纤维布滞后应变的计算方法,最后,通过对构件受力变形过程进行分析,计算其弯矩特征值,对界面应力进行分析,得出粘结剪应力方程、剥离应力方程,为实际工程提供参考作用。
1 碳纤维布加固钢结构试件破坏模形式
在实际工程中,碳纤维加固钢结构受弯构件一般情况粘贴于下翼缘,通过专用结构胶进行粘结,使组合构件共同受力,分担原构件的荷载,达到预期加固效果。根据相关试验及实际工程,组合构件的破坏形式主要分为三种情况[1-4],钢试件的弯曲破坏,碳纤维布拉断破坏、界面间的粘结破坏(见图 1)。
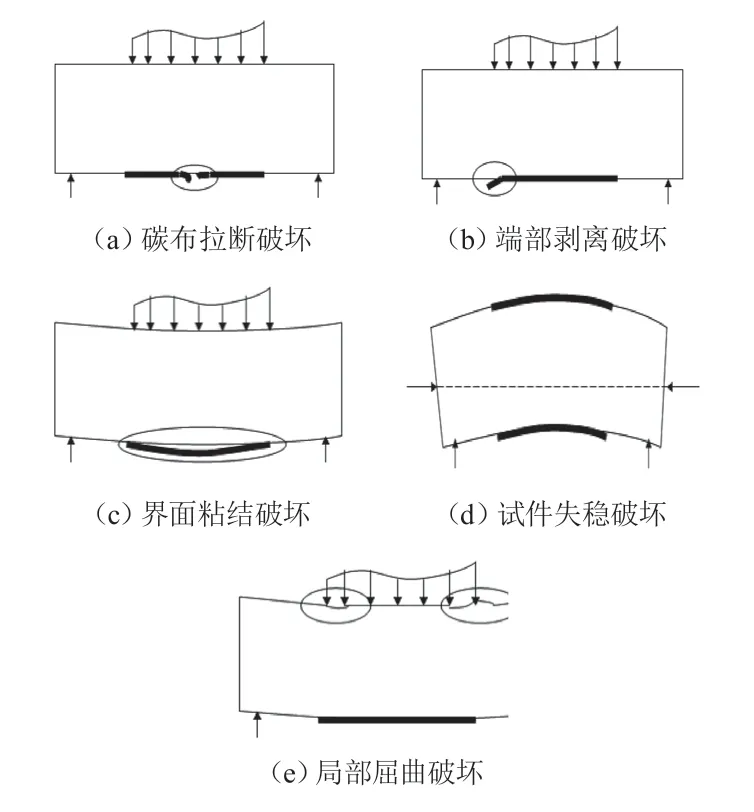
图1 试件的破坏形式
图 1 中①碳布拉断破坏:主要发生在当试件跨中弯矩达到最大值,碳布拉应力达到其极限应力,此时碳布发生拉断破坏的情况。②端部剥离破坏:碳布拉应力通过结构胶体的剪力来传送给原试件,从而达到加固效果,实际过程中往往会发生端部应力集中导致产生背离试件的剥离应力,最终试件发生剥离破坏,此时加固效果较低,实际工程中建议采取端部锚固措施避免此类破坏。③界面粘结破坏:碳布与试件主要通过结构胶来传递应力,实际过程中,粘贴施工质量较差或结构胶性能较差,此时界面为薄弱环节,容易发生粘贴破坏,此类破坏属于非正常破坏,为避免这种破坏,尽量采用正规施工工艺及性能较好的结构胶。④试件失稳破坏:试件达到其极限荷载阶段,试件可能发生侧向弯曲或扭转变形,为避免这种破坏,建议设计过程中对构件稳定性进行计算。⑤局部屈曲破坏:试件腹板及翼缘厚度过小,可能在失稳之前,试件翼缘或腹板发生凹凸变形,为避免这种破坏,建议可以对试件形状进行设计或承载点采取焊接加劲肋方式进行加强。
以上几种破坏形式,其中,碳布拉断破坏属于正截面弯曲破坏,端部剥离破坏和界面粘贴破坏属于非正常破坏,工程实际中尽量避免这种破坏,试件失稳破坏、局部屈曲破坏属于对试件未考虑规范构造措施导致的破坏。各种破坏形式的承载力计算方法也不相同,本文重点研究负载下试件的剥离破坏形式,通过对碳布滞后应变的计算,分析端部剥离破坏的机理,推定出粘结剪应力方程、剥离应力方程,为实际工程提供参考。
2 碳布滞后应变的计算
工程实际中,一般情况下对钢结构构件加固过程,构件未卸载,通过粘贴碳布以期提高承载能力,粘贴碳纤维布前期,其应变小于原构件应变,从而产生应变滞后现象。若忽略应变滞后现象,会导致对原构件的承载力评估过高[5-10]。本文依据钢结构理论及加固原理,对负载下粘贴碳纤维布加固钢结构构件计算方法进行了推定。
2.1 基本假定
1)原试件及加固后试件沿截面高度应变分布符合平截面假定。
2)试件为理想状态下的弹塑性材料,具体如图 2 所示。

图2 试件应力-应变关系

3)因为碳纤维布及结构胶厚度非常小,因此,加固前后试件截面高度可等效基本不变,试件梁底下翼缘滞后应变εpi和碳纤维布的拉应变εt近似相近。
2.2 计算公式
本文假定试件负载处于未达到屈服荷载,因此,试件受力区处于弹性阶段(见图 3)。

图3 试件应力应变关系
基于平截面假定,可以得式(3)。

式中:εc为受压翼缘边缘应变;εt受拉翼缘边缘应变;h为试件截面高度;y0为试件受拉翼缘边缘到中性轴距离。
由应力图可以得出式(4)及式(5)。

式(4)、(5)中,σt为受拉翼缘边缘应力;σcf为试件腹板与受压翼缘边缘应力;σtf、σc为腹板与受拉翼缘边缘应力、受压翼缘边缘应力;t为翼缘厚度。
试件合力作用点至中性轴的距离yci(m)、受压区合力Cci(N)分别为:
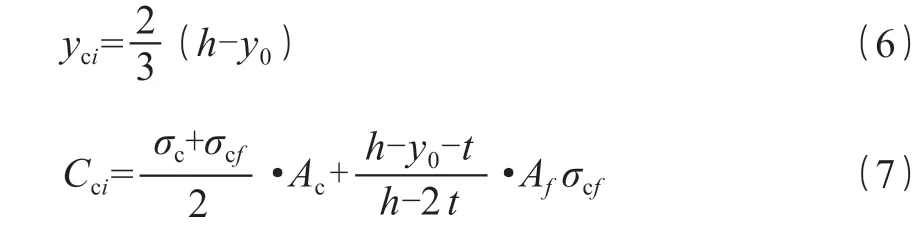
式(6)、(7)中,Ac为试件受压区翼缘截面面积;Af为试件腹板截面面积;其余符号与前相同。
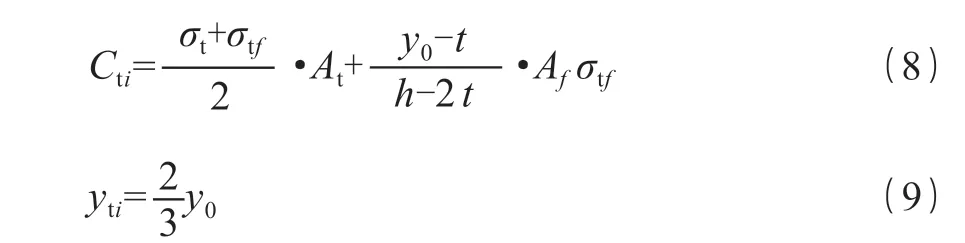
式(8)、(9)中,At为试件受拉区翼缘截面面积;其余符号与前相同。
由平衡条件可以得出:

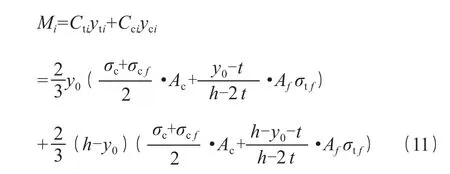
依据初始荷载下计算得到的初始弯矩,根据式(10)、(11),计算出试件受拉翼缘边缘到中性轴的距离y0及相应受压区翼缘边缘应变εc,从而可求出负载下碳布其滞后应变εc计算如式(12)所示。

3 试件受力变形过程分析
为进一步研究负载下组合构件受力变形过程,本文考虑材料的非线性本构关系,对构件受力变形全过程进行研究分析。
3.1 基本假定
为深入研究负载下组合构件力学性能,本文依据钢结构理论、结构加固理论,基本假定如下。
1)试验构件负载前后基本符合平截面假定;当构件服役时,依据实际荷载情况,按照第 2 章节的方法来计算碳纤维布的滞后应变。
2)组合构件界面粘贴牢靠。
3)试件应力应变按照 2.1 节中的假定。
4)碳纤维的应力σp等于碳纤维布的弹性模量Ep乘以其相应的应变εp,即:σp=Epεp,如图 4 所示。
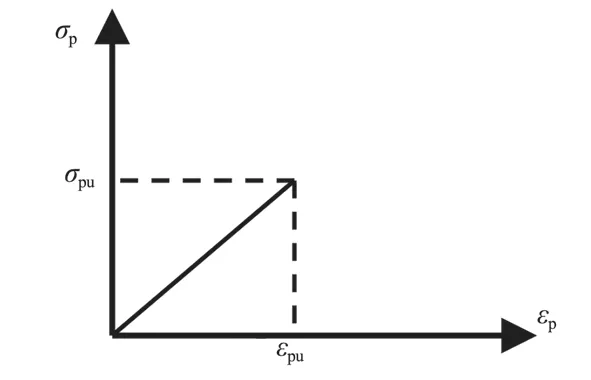
图4 碳纤维布应力-应变曲线
3.2 基本方程
基于分层法,对组合构件进行有限元计算,将试件沿截面高度分为n个应力均匀的条带,面积用ΔA表示,条带形心至试件截面中性轴的距离为y,如图 5 所示。假定中性轴以下y为负值,居于中性轴以上为正值,组合构件上应力,正值为拉应力,负值为压应力。
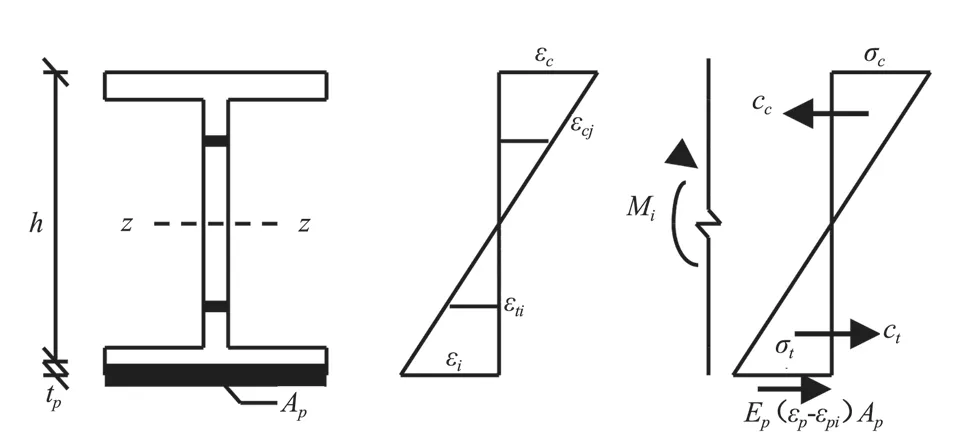
图5 负载下试件截面分层及其应力应变分布图
基于平截面假定,截面曲率φ计算如式(13)所示。

可以求出第i、j条形处试件处应变εci、εt及试件受拉翼缘、受压翼缘和碳纤维布的应变(εc、εt、εp)分别为:

式(14)~(18)中,εz为试件截面中心的z-z轴处的应变;tp、εpi为碳布的厚度、滞后应变,按公式(12)进行计算。
基于前节所述假定组合构件应力应变曲线,计算得出试件条带处、试件受力区、碳布上应力。通过静力平衡条件,计算推出截面弯矩M。
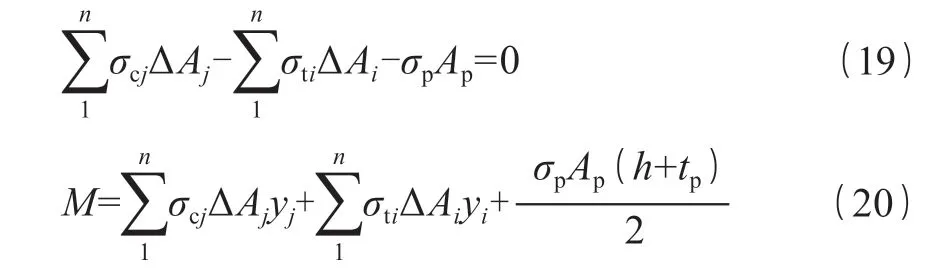
通过截面弯矩M、截面曲率的关系,分析其受力状态,进一步计算出截面任意处弯曲挠度,进而分析研究负载下组合构件受力变形过程。
4 弯矩特征值的计算
弯矩特征值即:在负载条件下,试件的屈服弯矩My、跨中挠度达到有效计算长度的 1/200 时所对应极限弯矩Mu、试件破坏时的破坏弯矩Mp。
根据本文第 3 章所描述,基于截面曲率的变化,计算出试件特征弯矩值,并根据 CECS77:96《钢结构加固技术规范》[12]、CECS 146:2003《碳纤维片材加固混凝土结构技术规范》[13]、GB 50017-2017《钢结构设计规范》[14]中的理论假定,推定出试件极限弯矩Mu、屈服弯矩My计算公式。
4.1 屈服弯矩的计算
根据图6,试件达到屈服阶段之前,此时下翼缘接近于极限拉应变εtu,此时有:

图6 截面屈服弯矩

式(21)、(22)中:xy为中和轴距上翼缘的距离;tp为碳布厚度;其余符号与前相同。
接近屈服阶段,此时试件处于弹塑性的界限阶段,试件应变沿截面高度呈线性关系,为方便计算,试件受力区域近似等效为三角形,具体如图 6 所示,通过静力平衡条件,推定如式(23)所示。

式(23)中:Ap、Ep为碳布截面面积、弹性模量;εpi为滞后应变;t为翼缘厚度;其余符号与前相同。
由式(21)~(23)可得试件弹性阶段截面中和轴位置高度,xy对中和轴取矩,推出试件负载条件下屈服弯矩的计算公式,具体如下式(24)。
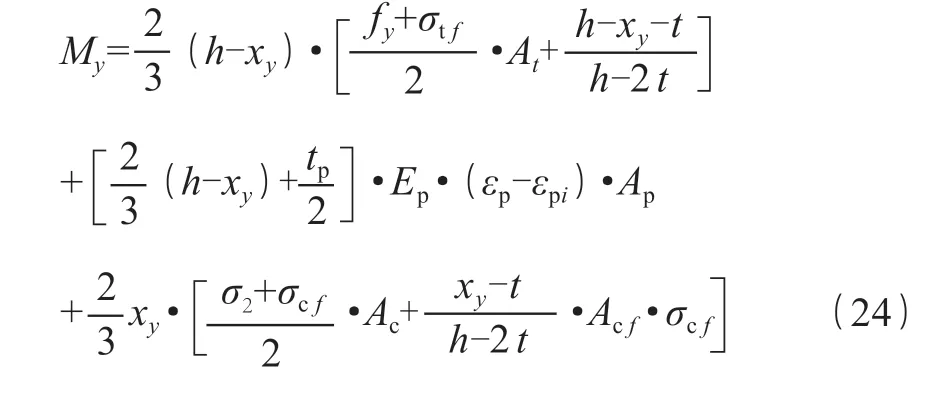
4.2 极限弯矩的计算
本文主要针对上下翼缘达到极限承载力、碳布拉断两种破坏形态,具体如图7。
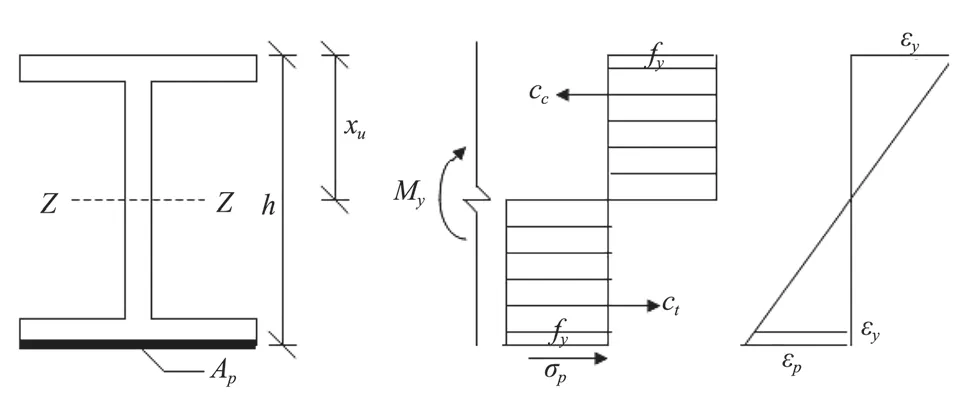
图7 截面屈极限矩计算
在此种破坏模式下,εp=εpu+εpi,其中:为碳纤维布的极限拉应变。受压区高度为h/2。因此,由截面静力平衡条件可以得到式(25)。
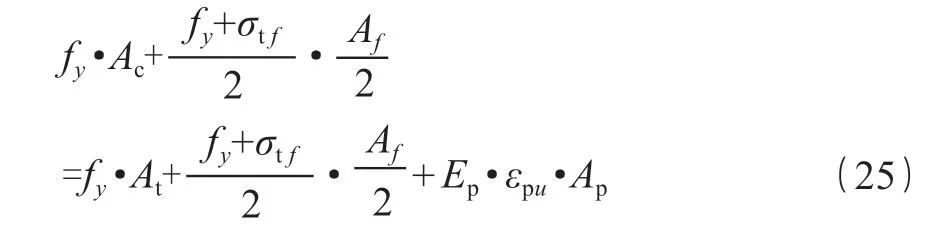
同理,对中性轴进行取矩,负载下试件极限弯矩计算公式推定如下式(26)。

5 试件的界面应力分析
对负载下试件进行粘贴碳纤维,主要通过碳纤维布与试件界面间粘结来传递有效应力,减小原试件应力,分担原试件荷载,以期达到加固效果,因此,界面处理在其中起到重要作用,现对界面应力方面进行分析,以期为实际工程提供科学有效依据。试件示意图,如图 8 所示。

图8 试件示意图
5.1 基本假定
为方便对组合试件界面分析,假定如下:
1)原试件理想成弹塑性材料,胶体、碳布理想成弹性材料;
2)组合构件上应变沿截面高度呈线性关系;
3)结构胶粘贴良好,厚度均匀,仅考虑剪切变形;
4)忽略碳纤维布、试件的剪切变形对界面应力的影响。
5.2 界面粘结剪应力分析
本节为方便对界面应力的研究分析,抽取一个理想单元体 dx,其具体受力状态如图 9 所示,依次对试件梁单元、结构胶单元、碳纤维布单元进行研究。

图9 试件、碳纤维布、结构胶单元受力图
5.2.1 梁单元体的受力分析
分析原试件梁单元体受力情况,受力分析如图 9 所示(a)所示,根据静力平衡,可得式(27)及(28)。
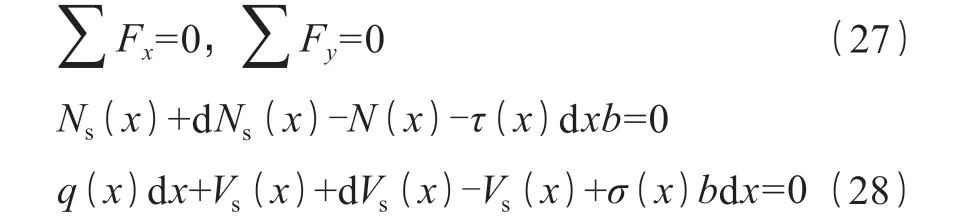
对梁单元体形心取矩,根据弯矩平衡条件可得式(29)及(30)。

联立方程(28)、(30)可以得到:
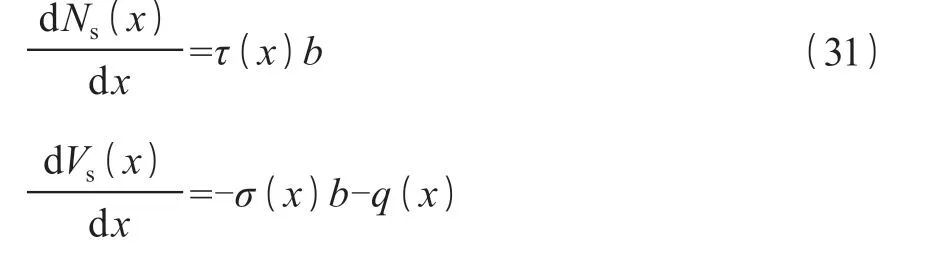

式(27)~(31)中:Ns为试件沿x轴的轴力;Ms为试件截面内的弯矩;Vs为试件截面内的弯矩;τ(x)为试件界面上的粘结剪应力;hc为试件形心轴到试件下翼缘下表面的距离;σ(x)为试件截面上的剥离应力;b为翼缘宽度。
引入物理方程可以得式(25)。

式(32)中:ws(x)、θs(x)、us(x)为横向位移、截面转角、轴向位移;Es、As、Is、αs为弹性模量、截面面积、截面惯性矩、横截面剪力系数。
5.2.2 碳纤维布单元体的受力分析
分析碳纤维布单元体受力情况,受力分析图见 9(c)所示,根据静力平衡,可得到以下:

式(33)中:Nc、Vc、Mc为碳纤维布的轴力、剪力、弯矩;tc为碳纤维布的厚度。
同理,引入物理方程可以得到:

式(34)中:uc(x)、ωc(x)分别为碳纤维布的轴向位移、横向位移;Ec、Ac、Ic分别为碳纤维布的弹性模量、截面面积、惯性矩。
5.2.3 结构胶体单元体的受力分析
分析结构胶单元体受力情况,受力分析图见 9(b)所示,结构胶体的剪应变计算公式如下:

式(35)中:ub(x)、ut(x)分别为胶体上下表面的水平位移;wa、ta分别为胶体的竖向位移和厚度。
结构胶体单元上下水平位移计算公式如下:

根据 5.1 中的假定,胶体理想成弹性材料,胶体厚度方向剪应力计算公式如下:

式(38)中:Ga为结构胶体的剪切模量。
由式(36)、(37)可以得出:

对式(38)微分,整理可得:

5.2.4 根据组合截面弯矩,计算可得组合构件曲率如下:

其中:Mt(x)为组合试件的截面弯矩;(EI)t为组合试件的抗弯刚度。
为方便分析研究,近似理想为原试件与碳布曲率相同,具体如下:

根据静力平衡条件,可以计算出式(44):

上式将剥离应力、界面剪应力进行综合耦合,因此,为方便计算研究,并对方程进行简化计算处理,最终推定出剪应力方程如式(47)所示。

其中,式中的系数C1、C2受试件的边界条件限制。
5.3 界面剥离应力分析
基于以上过程,结构胶体沿厚度方向法向剪应力、正应变计算公式如下:

式(48)及(49)中:Ea为结构胶体的弹性模量;wc(x)、ws(x)为分别为碳纤维布和试件的竖向位移。
对式(48)进行微分:

联立式(32)可以得到:
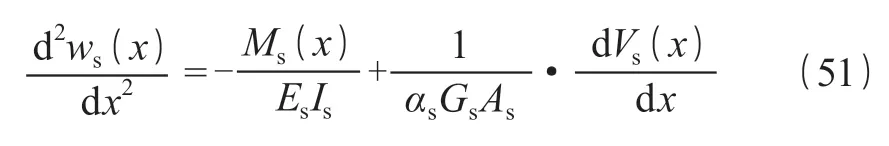
联立式(34)、(50)、(51)并对其进行微分处理可以分别得到式(52)、(53):

可忽略部分较小的系数,将式(53)进行简化处理,具体如下:

其中式中的β4可以按式(55)进行计算:

对式(54)进行微分处理,可推出界面剥离应力计算公式,具体如下:

其中,f(x)按式(57)进行计算:

实际过程中,x与剥离应力呈反比,x增大,剥离应力逐步趋于零,有D3=D4且D1、D2由边界条件来确定,则式(56)可以简化为:

6 结论
1)对碳纤维加固钢结构的破坏形态进行了详细描述。
2)根据实际受力状态,依据钢结构理论、加固原理,本文简要描述了加固过程中滞后应对对构件承载力影响,并对滞后应变公式进行推定。
3)考虑到材料的非线性本构关系,通过对试件弯矩、曲率关系进行分析研究,对负载下加固构件的受力过程进行分析研究。
4)基于对负载下加固构件的受力过程,推定出此类组合构件的极限荷载、屈服荷载计算公式。
5)基于对组合构件各单元受力状态的分别分析,进而对粘贴剪应力、剥离应力有整体了解,最终推定出粘结剪应力方程、剥离应力方程。Q

