基于层次分析与变权原理的空间钢结构健康状态研究

袁金兴，丁双双，孙 亚，李祖辉，缪明明

（1.苏州中正工程检测有限公司，江苏 苏州 215026；2.如东恒正建设工程质量检测有限公司，江苏 如东 226400；3.苏州科技大学，江苏 苏州 215000）

0 引言

现有的空间钢结构的健康监测研究主要集中于加速度、竖向变形、应力应变等评价指标，对于结构的安全性评价仅通过对构件实测值与理论值分别进行比较，多个评价指标相互独立，以单构件的安全与否，评价整个结构的健康状态［1-3］。此外，对不同重要性程度的监测对象，采集数据的评价权重固定统一，无法适应空间钢结构的多变复杂的结构体系，得出的评价结果的可靠性有待商榷［4，5］。本文基于层次分析与变权原理，对大跨空间钢结构健康状态的评价方法进行研究，提出一种可以根据构件重要程度采用不同权重、多评价指标共同参与评价的综合评价方法。

1 层次分析法

层次分析法是一种多个指标综合评价的方法，可以最大程度减少主观因素或者偶然因素的影响。它将研究对象看作一个系统，通过分解、比较判断、综合分析等方法，将复杂的问题按照属性的不同划分为相互联系且有递阶关系的不同的层次。同一层次的各评价指标赋予初始的量值，利用数学方法计算各层次的所有元素的权重，依照递阶关系，依次从底层向最高层进行分析问题［6，7］。

层次分析法的操作步骤如下。

1）明确目标，确定评价指标及评价标度。

对需要评价的对象进行分析研究，确定影响评定结果的主次因素。确保主要因素无遗漏，次要因素所赋权重不会过大。

2）建立递阶层次。

将需要研究的对象层次化，建立递阶层次结构。按照项目之间的隶属关系，层次一般分为目标层、准则层、方案层。例如空间钢结构的健康状态评价，目标层为整个空间钢结构的评价分数；准则层为应力评价分数，挠度评价分数，模态评价分数等；方案层为各监测对象的监测数据。

3）构建各层的判断矩阵。

按照同一层次中各因素的重要程度进行定量赋值。对于空间钢结构可以通过专家根据经验赋值或者各种模拟计算方法确定。将赋值的各元素构建成符合一致性条件的判断矩阵。例如对层次A的各影响因素A1，A2，…，An构建如表 1 的判断矩阵。

表1 层次 A 的判断矩阵

层次A构建的判断矩阵需要具有一致性的特点，即矩阵对角线各元素值为 1；对角线上三角与下三角对应的赋值互为倒数；影响因素Ai比Ai-1具有优先权重。

4）采用幂法计算各元素的相对权重。

得到判断矩阵A后，最为关键就是求出权重向量，层次分析法一般采用和法或者幂法。对于空间钢结构的健康状态评价，本文采用幂法。通过将A的各个列向量首先进行几何平均计算后，然后将得到的新向量归一化处理后得出的列向量就是权重向量。计算公式如下：

式中：aij为影响因素Ai对影响因素Aj的重要程度赋值。

对于一个复杂问题，人们的主观认识具有片面性，主观性、随意性，构建的判断矩阵中影响因素Ai比Ai-1具有优先权重实现起来比较困难，完全符合一致性条件几乎不可能。一般通过计算判断矩阵的最大特征根λmax，引入三个判断指标检验一致性条件，校核判断矩阵是否进行调整。

式中：A为判断矩阵，λmax为最大特征根，ω为最大特征根对应的特征向量。

（a）一致性检验指标CI。

式中：n为判断矩阵的阶数。

（b）平均随机一致性指标RI。

矩阵阶数的不同和判断矩阵重复计算次数的不同，对应着不同的平均随机一致性指标，表 2 为 1～10 阶判断矩阵重复计算 1 000 次后，平均随机一致性指标。

表2 平均随机一致性指标RI

（c）相对一致性指标CR。

一般认为CR≤0.1 时，认为判断矩阵符合一致性要求，否则不满足，应修改判断矩阵。

2 变权综合原理

对于复杂空间结构的评价，需要综合考虑诸多影响因素。现有的空间钢结构监测体系，对于同一层次的同一评价指标权重恒定，即采用常权分析法对结构健康状态进行评价。其具有一定的局限性：空间钢结构各种构件的重要程度不完全相同；同类构件，安全储备不尽相同，容变量不同。因此，根据构件在相同工况下的各构件的安全储备，变权综合法应当用于评价指标权重的调整。

2.1 基本原理

式中：α为变权系数，0＜α≤1，当α=1时，即为常权公式。

2.2 变权系数α的确定

变权系数α的取值反映了决策者对于监测指标优缺点的均衡性的要求。α值越大，表明决策者对于监测指标的优点越重视，对其缺点比较漠视。α值越小，表明对缺陷的容忍度越小。在确定空间钢结构健康状态时，首先可以确定各项指标的最低评价值，当所有指标均高于该评价值时，可以确保结构的安全，当任一指标低于该值时，结构的安全性得不到保证，以此来反算α值。一般认为，当 0.2≤α≤0.5 时，可以满足大多数工程要求。

3 层次分析法应用于空间钢结构

3.1 工程概况

趣店科技金融创新园区项目基地位于厦门市同安区与集美区交界处，环东海域东部新城、滨海西大道与美社路交叉口东侧地块。主楼为一幢 9 层的综合办公楼，建筑高度 48 m，主楼平面呈回字形布置，结构外边尺寸 139.2 m，内边尺寸 84.0 m。主体由核心筒、楼层钢梁、巨型拱、水平桁架和吊柱组成，采用钢骨混凝土筒—巨型拱悬吊结构体系，主楼下部为不规则曲屋面裙房。东南西北 4 条边上各设置 2 个，总计 8 个钢骨混凝土核心筒。核心筒之间设置巨型折线拱，拱上部及中部分别设置水平桁架和拉梁，拱下部设置拉索共同形成自平衡体系。钢梁楼面通过吊柱传递给巨型拱，如图 1、图 2 所示。

图1 结构三维示意图

图2 吊柱及钢梁结构立面示意图

3.2 结构的有限元模型

结构的质量、刚度、边界条件的精确模拟对于空间钢结构的健康监测至关重要。其直接影响建模结构的动力特性，理论值与监测值的拟合程度。健康监测要求有限元的模型在真实反映结构几何与物理特征的基础上，谋求正确反映结构的静力与动力特性。对于趣店项目采用 MIDAS/GEN 有限元分析软件，建立分析模型，如图 3 所示。

图3 趣店项目 Midas 模型

3.3 监测项目与监测位置的确定

如图 4 所示，本工程主楼上部设置两层水平桁架，八层由核心筒之间结构向内外各悬挑 9 m，上下层桁架间通过箱型钢柱和斜拉杆连接。巨型拱位于 8 个核心筒之间，单跨拱长约 57 m。直线段拱脚设置 4 根Φ125 mm 拉索，拱上部设置箱型水平梁共同形成自平衡体系。根据结构形式将整个结构分为八个监测分区，如图 5 所示。通过模型分析，对巨型拱、吊杆、桁架上下弦，腹杆等布置 96 个单通道正弦式应力采集装置，32 个位移采集点。对分区一、二内外吊杆布置 4 个加速度传感器。

图4 巨型拱构成的 8 个分区

图5 结构的监测分区

3.4 应力监测的层次分析

3.4.1 应力监测分区权重

先进的数据采集系统和存储系统，在钢结构健康监测中，采集了海量的应力监测数据。假如未能对海量数据进行科学合理的处理，反而容易造成监测系统的误导作用［8］。截面位置不同、强度储备不同，使各个应力监测截面与测点的权重是不能完全相等对的。采用各监测截面在不同工况下所剩的强度储备（极值差值的最小绝对值）确定截面与测点的权重，能够更加客观地评价空间结构的健康状态。根据模型计算 8 个分区的各个截面的应力极值与强度储备，如表 3 所示。

根据表 3，取出 8 个分区的极值差值绝对值两两比较确定递阶关系为：146，170，179，183，197，213，225，238，构建一个符合一致性的条件的判断矩阵。

表3 分区应力极限值表 MPa

采用幂法计算各分区的权重，第一步：按照列相乘得到一个新向量。

第二步：将新向量的每个分量开8次方。

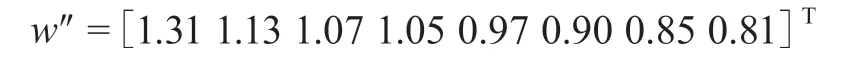
第三步：将所得向量除以向量的代数和即得到权重向量。

表4 应力监测分区权重

3.4.2 各监测截面测点权重

桁架结构的腹板、上下弦杆、拉杆受力复杂，各自承担的角色各不相同，各监测截面的权重同样不能取相同的权重。按照上面的方法计算各分区上各个监测截面的强度储备，如表 5、表 6 所示。

表5 各分区各监测截面应力极限表 MPa

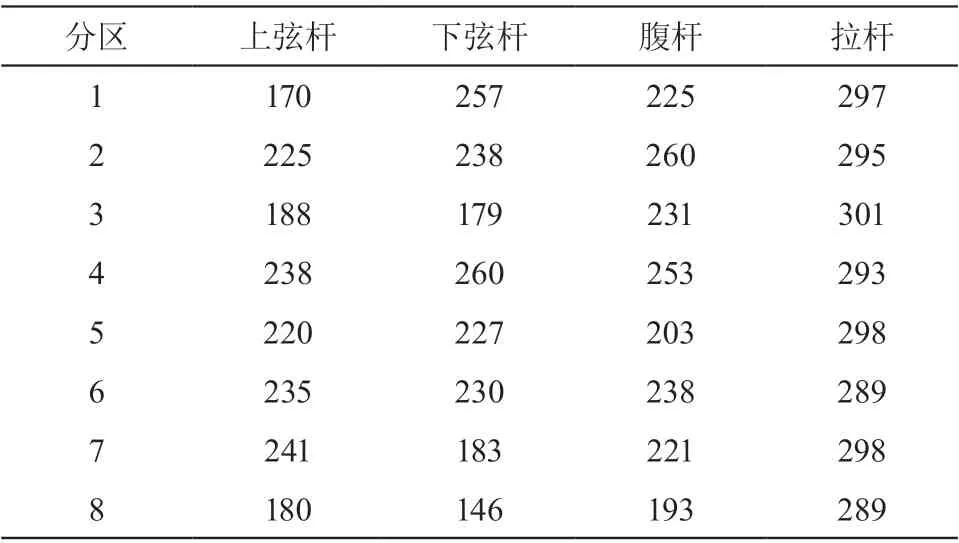
表6 各监测截面强度储备 MPa

通过幂法计算，并满足一致性条件，得到各分区监测点的权重，如表 7 所示。

表7 各监测截面权重

将分区权重与各分区的测点权重相乘，可以得到各测点在整个空间结构应力状态评价的权重，如表 8 所示。

表8 各分区测点权重

3.5 应力监测的变权分析

为了准确把握空间结构在施工阶段的损伤、安装误差、焊接缺陷等不确定的危险因素，修正以理想的有限元模型为基础建立的层次分析法，引入一种更加客观、使用范围更加广泛的变权分析法。

3.5.1 各监测分区测点应力上下限值

为了更加合理客观地使用变权原理分析修正层次分析法，应根据实际荷载组合下，实测应力值与理论模型的阈值进行对比分析。对于已经投入使用的空间钢结构，变化因素为活荷载与环境因素，各分区的应力上下限值可以取自重作用下的安全储备作为阈值，基准值取为 0。在 1.0 活荷载组合下，各分区的阈值如表 9 所示。

表9 各分区各监测点的阈值 MPa

3.5.2 评价指标值

取 2021 年 12 月 5 日 10∶34 的监测数据，进行评价指标值计算。表 10 为各个分区的安装监测传感器的监测点位置与阈值差值绝对值最小的应力值。

表10 各分区各测点实测应力值 MPa

应力数据属于一系列有量纲的数值，将其按照式（6）进行无量纲处理。

式中：x0为基准值，xmax为上限值，xmin为下限值。

通过无量纲计算，得到各分区各监测点的评价指标值如表 11 所示。

表11 无量纲处理后各测点的评价指标值

3.5.3 变权修正后的各测点的权重值

变权修正的核心思想就是将评价指标值较低的权重进行惩罚，重点考虑该评价指标，按照公式：

将分区各个测点进行变权修正，式中α=0.2。具体如表 12 所示。

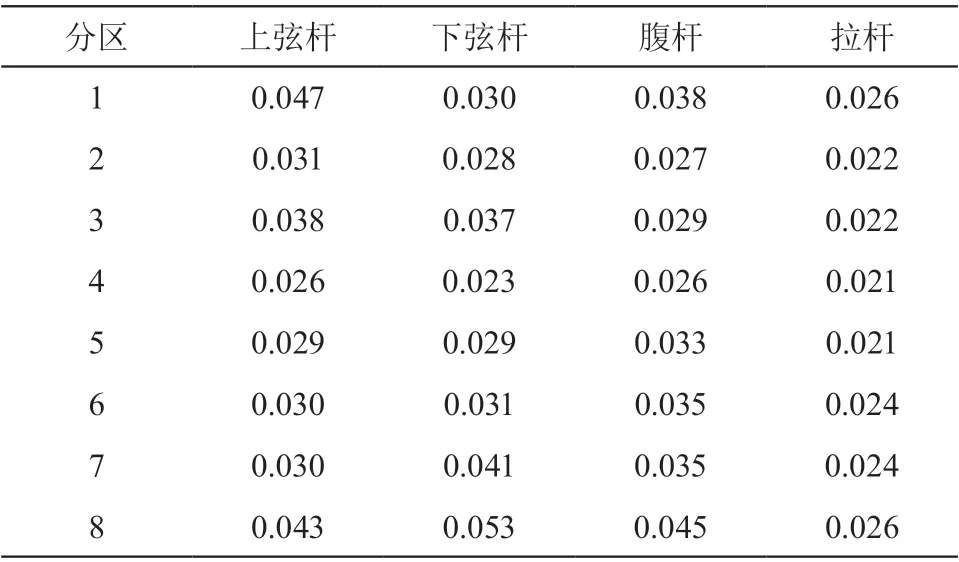
表12 变权修正后各监测点的权重值

3.6 空间结构应力总体评价

通过层次分析和变权修正后，将各分区各监测点的评价指标值与评价权重相乘，得到空间钢结构应力值的总体评价。厦门趣店项目空间钢结构的的应力健康状态总体评分为：

由于篇幅所限，空间钢结构评价指标不限于钢结构应力，还包括结构挠度、模态等。但是通过层次递阶与无量纲处理后，可以将不同的评价指标归一至同一评价体系中，从而更加全面地评价空间钢结构的健康状态。

4 结语

1）通过层次分析法和变权原理，对厦门趣店项目应力健康状态进行了总体评价，其应力健康状态良好。

2）层次分析法与变权原理可以为空间钢结构的健康监测评价提供理论支撑。层次分析法将复杂问题逐层递阶分解，层次分明，容易理解，变权原理修正了有限模型理论分析与实际施工相差较大的影响，评价更加客观合理。

3）层次分析法与变权原理，采用无量纲的分析方法，可以将不同的评价指标归一至同一评价体系，避免了单一评价指标的偶然性，可靠性得到较大的提高，评价结果具有较大的可信度。Q