基本事件:辨析古典概率问题的关键
郑 燕
西华师范大学数学与信息学院
在古典概率的学习中,学生总是容易混淆“非等可能”与“等可能”、“有放回”与“不放回”问题,究其原因就是对试验所包含的基本事件的认识存在问题.针对这种情况,笔者从具体案例入手分析如何从基本事件角度解决问题.
1 “非等可能”与“等可能”
例1同时掷两枚骰子,求向上的点数之和为5的概率.
正解:设向上的点数之和为5的事件为A.把两个骰子标上记号1,2以便区分,试验所包括基本事件如表1所示.
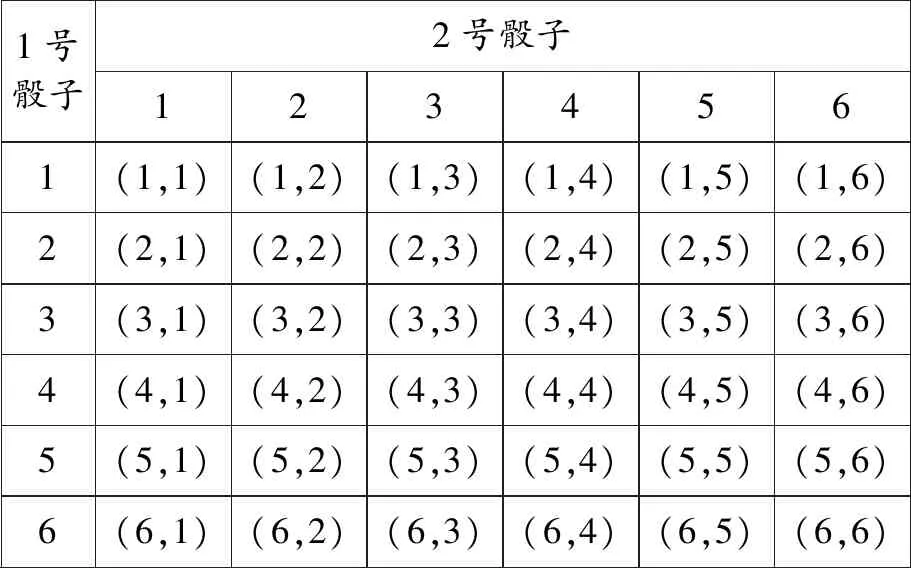
表1 一次试验包括的基本事件

错解:设向上的点数之和为5的事件为A.两个骰子不标识,则可列出基本事件如表2所示.
从表2可以知道一次试验包含的基本事件有21个,向上的点数之和为5包含的基本事件有(1,4),(2,3)共2个.

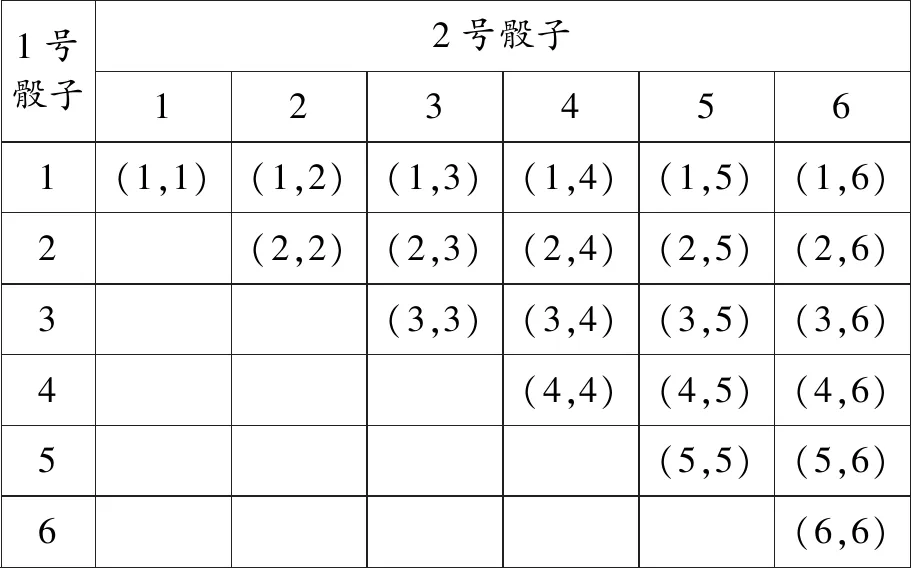
表2 一次试验包括的基本事件
这两种解法如果从等可能的角度来判断,显然第二种解法错误.但是实际情况是学生不能区分基本事件是等可能发生的还是非等可能发生的.因为他们对于试验所包含的基本事件的定位都不清楚,不知道基本事件由哪些元素构成.要弄清楚基本事件的构成,就要追根溯源,弄清基本事件的形成过程[1].正解中试验的基本事件是由骰子的点数构成的,即1号骰子的每一结果与2号骰子的任一结果匹配.所以每个基本事件的发生都是等可能的,且他们的结果是有限的,因此可用古典概率的计算公式计算.错解中事件A的基本事件是由点数和为5的事件构成,而在这里面构成5的比如有(1,4),(4,1)两种,但如果只看结果“和为5”的话,就认为(1,4),(4,1)这两种结果是一样的,只把其中一个当成基本事件,实际上错解中每个基本事件的发生都是非等可能的,这时使用古典概率公式就会计出错.
2 “有放回”与“不放回”
例2设袋子中有3个黑球,2个白球,它们除颜色外没有区别.
(1)从袋子中不放回地随机摸出两个球,求两个球都是黑色的概率.
(2)若从袋子中随机取一个球记下颜色后放回袋子中,再随机摸一个球,求两次摸到的球都是黑色的概率.
对于第(1)问,先将5个球编号为1,2,3,4,5.其中编号为1~3号的球为黑球,编号为4,5的球为白球.记两次摸到的球都是黑色为事件X.第(1)问有 “分次摸球”与“一次摸出两个球”两种方法.
方法1:“分次摸球”包含的基本事件如表3所示.

表3 基本事件
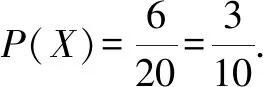
方法2:“一次摸出两个球”包含的基本事件如表4所示.
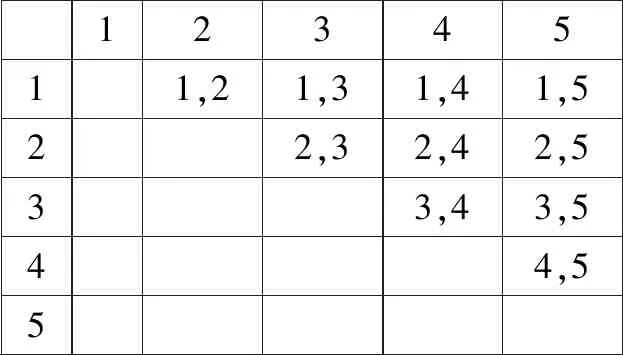
表4 基本事件

从“分次摸球”和“一次摸出两球”的基本事件来看, “分次摸球”的基本事件是由第一次摸球颜色与第二次摸球颜色的任意结果组成,每个基本事件发生是等可能的.“一次摸出两球”的基本事件是由一次摸出的两球的颜色组成,一个基本事件就是一次摸球的结果,且一次摸出两球是等可能发生的.从基本事件分析可知这两种方法都是正确的.比较这两种方法,虽然“随机摸出两球”包含的基本事件不同,事件X包含的基本事件也不同,但它们的基本事件都是等可能发生的,且二者利用古典概率计算的结果是相同的,因为它们的计算过程都满足古典概率的概率公式的计算要求.这就说明对于“不放回”摸球类型问题,在考虑解题方式时,从“有序”或“无序”入手求解的结果相同.再遇到这种问题时,只需两种角度二选一即可.
对于第(2)问,属于有放回的摸球.将3个黑球编为1~3号,白球编为4,5号.记两次摸到的球都是黑色为事件A.第(2)问也从“有序摸球”与“无序摸球”分别入手.
正解:“有序摸球”.第一次摸出的球与第二次摸出的球有先后之分,包含的基本事件如表5所示.
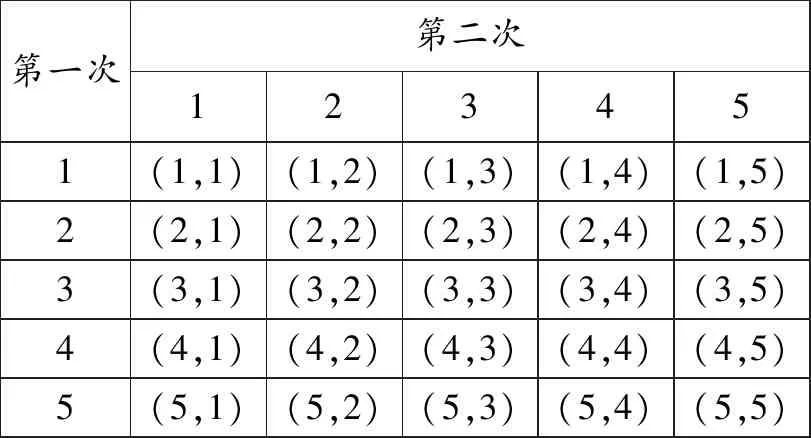
表5 基本事件
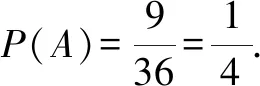
错解:“无序摸球”.在列基本事件时第一次摸的球与第二次摸的球视为无序,只要摸出两个球即可,包含的基本事件如表6所示.
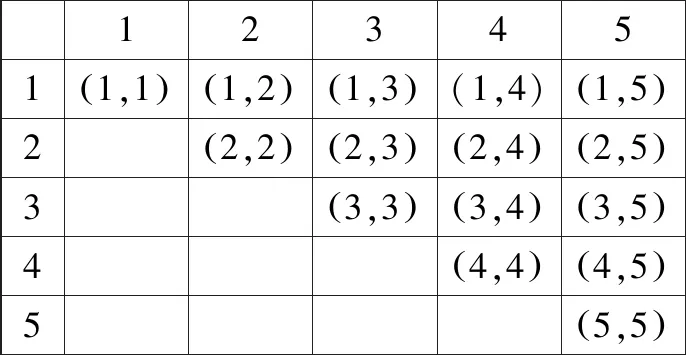
表6 基本事件
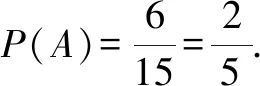
类比例1,“有序摸球”的基本事件是由第一次摸出的球和第二次摸出球的颜色组合而成,且它们发生都是等可能的.“无序摸球”的基本事件是由摸出的两球的颜色构成,这个基本事件不是等可能发生的.所以对“有放回”摸球问题,在考虑解题方式时,必须强调“有序”,因为“无序”不能满足基本事件的等可能性.
3 总结
从上面的分析可以看出,基本事件在解决概率问题时起着关键作用.所以在平时的教学中,教师不仅要教学生基本事件的概念,还应该分析基本事件的形成过程.为了让学生了解基本事件的形成过程,在对基本事件进行分析时,可借助树状图、列图表等形式罗列基本事件,以便学生在罗列时判断基本事件是否等可能发生.对于基本事件较少的随机试验,教师可以在课堂上开展“游戏”活动,使学生在游戏参与中体会基本事件的形成过程.教师也可以在课堂上进行多媒体演示,比如同时掷两枚骰子的问题,可以通过多媒体演示,使学生明晰基本事件的形成过程.学生只有在理解试验的基本事件形成过程后,对于基本事件的选择才不会出错.
——两球与墙壁三者间的碰撞次数与圆周率π间关系的讨论

