双自由度PID-III型锁相环在新能源系统的应用
王晓东,杜 鹃,倪喜军,王霁莹,闫 芳
(1.国网山西省电力公司长治供电公司,山西 长治 046011;2.南京工程学院 电力工程学院,江苏 南京 210067)
0 引言
随着光伏发电和储能技术的快速发展,越来越多的逆变器并入配电网,实现电能上网和无功调节。逆变器依靠锁相环 (Phase-Locked Loop,PLL)获得电网电压的频率、相位和幅值信息[1],因而锁相过程是并网的前提和基础。理想条件下,PLL能够通过自身的闭环控制实现电网同步信息跟踪,但在电网电压不平衡、包含谐波和直流分量后,PLL的动态响应速度、精度等性能就会恶化。近年来,含分布式电源配电网建设加快发展,但部分区域农网电能质量仍然很差[2],随着国家“光伏扶贫”“县域光伏”政策的推广,大量的逆变器并入农村弱电网,由于PLL不能正常工作而导致逆变器频繁跳闸的问题不断出现,影响配电网安全和居民收入。
传统的单同步坐标系PI锁相环技术(Single Synchronous Reference Frame-Phase-locked Loops,SSRF-PLL)[3]~[6]虽 然 控 制 简 单、响 应 快,但 在 电 网电压不平衡、存在谐波和直流分量时,锁相误差较大。通过二阶广义积分器(Second-Order Generalized Integrator,SOGI)[3]、陷 波 器[4]、平 均 值 滤 波 器[5]、重复内模[6]等方法调整环路滤波器系数可降低上述误差,但附加的带宽降低将影响PLL响应速度,进而影响逆变器的并网性能。一种解耦双同步坐标系锁相环技术[7](Decoupled Double Synchronous Reference Frame PLL,DDSRF-PLL)利用正负同步坐标分离正负序分量,有效抑制电网电压不平衡,但直流分量影响仍然未能解决。文献[8]提出了5种消除直流分量的方法,其中:两种利用旋转坐标和静止坐标的延时信号消除技术,类似于平均值滤波器功能,但需要实时自适应更新电网频率对应的延迟周期;其余采用自适应陷波器、复系数和交叉反馈网络,实现过程均复杂,参数整定困难。文献[9]提出了基于3阶SOGI的直流分量滤除技术,相对2阶SOGI-PLL增加了单独的直流检测回路,但该结构的频域建模复杂且物理意义不明确。文献[10],[11]提出基于平均值和组合滤波器PLL,具有较好的抗干扰性能,在PLL领域获得一定应用,但其仅考虑快速响应的超前补偿,未考虑加速度信号的跟踪和复杂的抗扰动能力。文献[12]提出一种3阶PLL,解决了加速度信号的跟踪问题。文献[13],[14]提出了3阶系统的设计方法,提高了带宽。上述文献虽然能够解决加速度信号的跟踪问题,但其仍未对扰动性能做优化处理,且参数整定方法经验要求高。
二自由度PID[15]可以分别设置跟踪和抗干扰的参数,在控制领域获得广泛应用。本文结合二自由度PID整定方法和III型PLL的“内模”原理,提出了一种基于双自由度PID补偿的III型PLL技 术(Type-3Phase-Lock-Loop Based on Two Degrees of Freedom PID Compensation,2DOF-PID III-PLL),兼顾PLL加速度信号跟踪和抗干扰的性能,经仿真验证其有效和实用。
1 PLL模型
1.1 PLL基本原理
PLL主要由鉴相器、环路滤波器和压控振荡器(VCO)组成。本文研究的软件PLL由Park变换实现鉴相,积分型压控振荡器完成相位输出,由于环路滤波器有不同的类型,其性能优劣与类型关系较大。
为推导PLL传递函数,假设配电网电压如下:
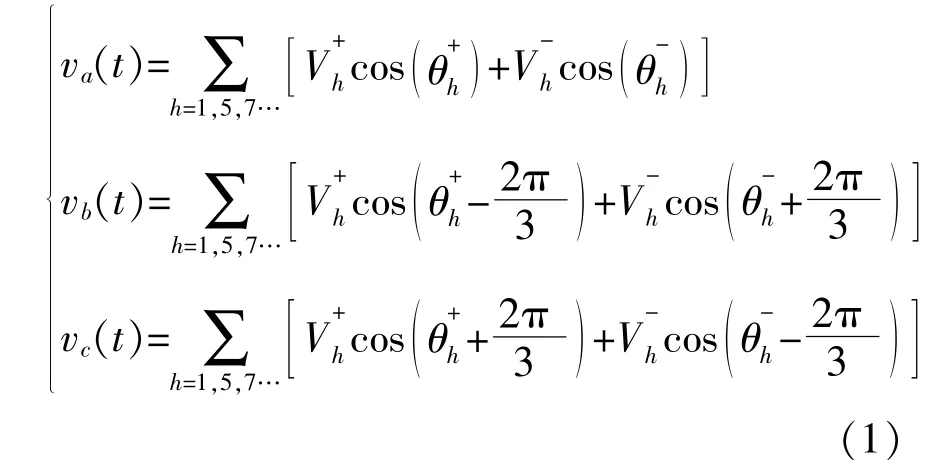
由于配电网电压中偶数次分量较小,此处只考虑电压奇数次谐波;PLL采集初始阶段会采用初始值直流分量消除技术以及利用滑动平均值滤波器消除Park变换的谐波分量,因此忽略电压中的稳态直流分量。
利用Clarke变换将式(1)转换为静止二坐标系变量,可得:
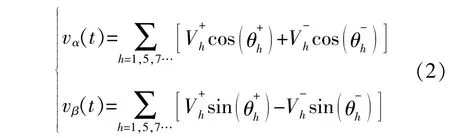
进一步采用Park变换,可得:

将式(3)的高频项归并,并假设此时PLL已完成锁相,则式(3)的q轴分量可改写为
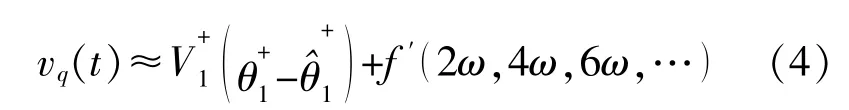
其中高频项f′当作PLL的扰动量。
通过上述推导,可获得常规SSRF-PLL传递函数,如式(5)所示,此处滤波环节采用一阶低通滤波器,并通过PI补偿实现控制环路校正。
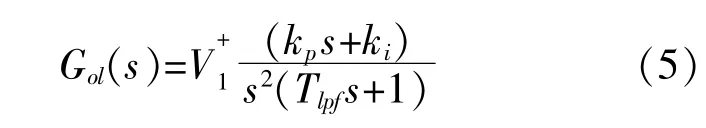
式中:kp和ki分别为PI补偿环节的比例和积分系数;Tlpf为一阶低通滤波器的时间系数;为正序基波的幅值;s为拉普拉斯算子。
由式(5)可知,电压幅值影响PLL的带宽,当配电网电压跌落时,会导致PLL不稳定。为此,文献[12]提出利用d轴分量标幺化q轴分量的方案,实现了PLL带宽与电压幅值解耦,提高了配电网电压跌落时PLL的鲁棒性。文献[12]进一步利用反正切运算,实现d轴分量与角差的完全线性化。该类PLL为一典型II型系统,其参数可参考“模最佳系统”方法整定,该类系统虽然具有较好的抗扰动能力,但其跟随阶跃指令时超调较大,未能优化。典型II型系统具有两个积分环节,根据“内模原理”[16],其对相位和频率阶跃可以做到无静差跟踪,但无法对加速度性质的频率变化信号实现完全无静差跟踪。
1.2 滤波器
常规SSRF-PLL使用PI补偿环节替代常规滤波器,虽然简单,但该PLL的滤波和响应能力一般,很难应付复杂环境。部分PLL使用某个或多个陷波器作为滤波器[4],[8],可有效滤除特定次谐波,但很难应付复杂时变的电网谐波。SOGI[3]的等效传递函数如式(6)所示,分别为二阶低通滤波器和二阶带通滤波器,具有滤波功能,通过设置参数k和 ωc可消除一定的电网谐波影响,但SOGI直流滤除能力一般。
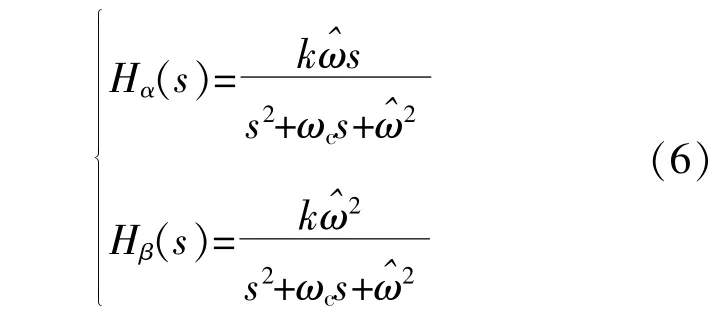
文献[10]采用滑动平均值滤波器,其传递函数如式(7)所示,推导系统传递函数时可等效为一阶低通滤波器。
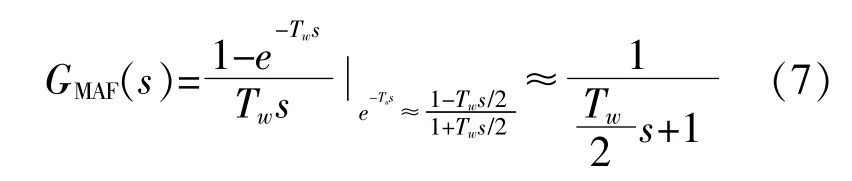
如图1所示,伯德图表明平均值滤波器可以滤除与设置的窗口时间相关的整数次谐波,具有类似无限个陷波器叠加的功能,相对SOGI和陷波器有明显的优势,且软件实现简单。因此本文采用滑动平均值滤波器。
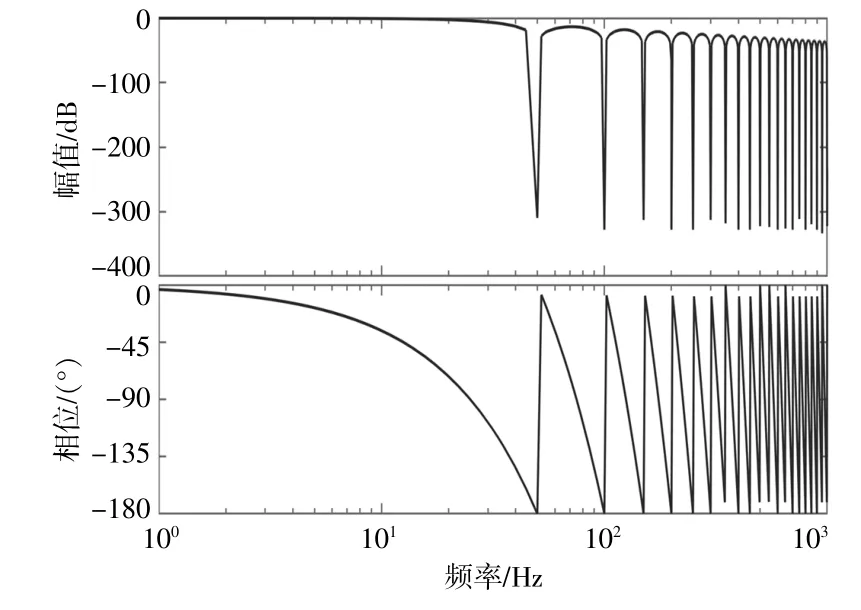
图1 窗口时间0.02s的平均值滤波器伯德图Fig.1 The MAF Bode plot of window time0.02s
1.3 双自由度PID
传统PLL使用单自由度PI补偿器,其跟踪和抗干扰性能只能折中,两者无法完全独立设置。如图2所示的双自由度PID控制系统,通过设置不同的前馈和反馈回路,实现跟踪和抗干扰性能参数分别设置,具体传递函数如下:
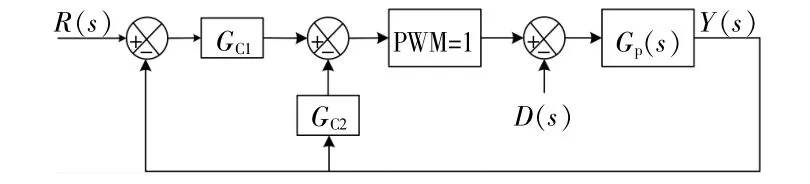
图2 双自由度PID控制系统Fig.22 DOF-PID controller system
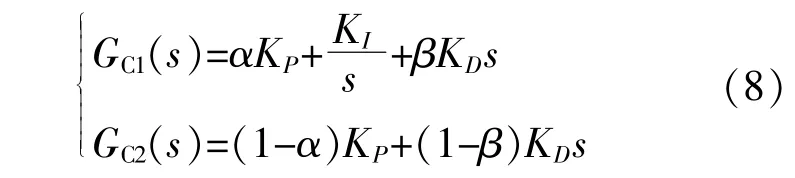
式 中:GC1(s),GC2(s)分 别 为 前 馈 和 反 馈 补 偿 器,两者之和为传统的单自由度PID控制器;KP,KI,KD分别为比例、积分和微分系数;α,β为双自由度化系数。
由 图2可 得 参 考R(s)和 扰 动D(s)对 输 出Y(s)的 闭 环 传 递 函 数。如 式(9)所 示,两 者 的 分 母一 致,但Gyr(s)比Gyd(s)多 了 一 个GC1(s),即 基 于双自由度PID补偿的Gyr(s)增加了一个额外控制自 由 度GC1(s)。因 此 先 设 计PID[GC2(s)+GC1(s)]参数实现闭环系统抗扰动特性调节,再优化设计GC1(s)就可单独实现闭环系统输入参考跟踪特性调节。
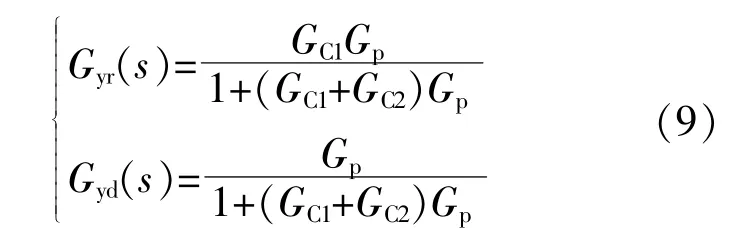
2 所提PLL结构和特性分析
2.1 所提PLL结构
本文提出的基于双自由度PID的III型PLL结构如图3所示。为了增强跟踪加速度信号的性能,在前向通道中增加一个额外积分器,使PLL总开环传递函数包含PID积分器、额外积分器、积分型压控振荡器3个积分器,即包含加速度信号模型。根据“内模原理”可知,该系统能够无静差跟踪加速度信号。此外,为抵消额外积分器的相移,在前向通道增加一个用于抵消MAF滤波器等效极点的零点,增加PLL的裕度和稳定性。
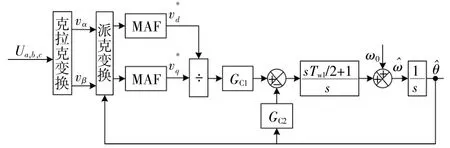
图3 基于双自由度PID的III型PLL结构Fig.3 Type-III PLL structure based on2DOF-PID controllers
额外增加的零-极点传递函数如下:
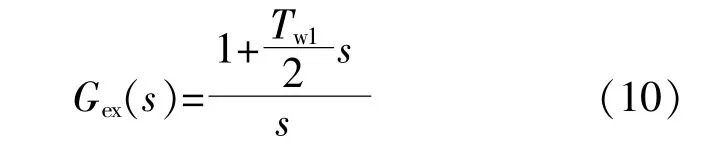
式中:Tw1为0.02s,虽然实际配电网频率有变化,但变化很小,Tw1与系统周期可近似相等。
2.2 等效传递函数
由 图2、图3以 及 式(10)可 得 如 图4(a)所 示的基于双自由度PID补偿的III型PLL系统传递函数图。

图4 系统传递函数图Fig.4 System transfer function
考虑Tw1与系统周期近似相等,即MAF滤波器等效极点和额外零点相互消除,可得如图4(b)所示的简化图。将控制对象等值传递函数Gp=1/(s2)和 式(8)代 入 式(9),可 得 如 下 改 进 的 闭 环 传递函数:
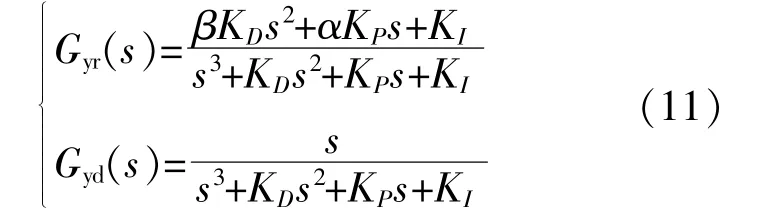
2.3 参数设计及稳定性分析
由式(11)可知,如果满足Gyr和Gyd特征多项式在s域右半平面无闭环极点,就可保证参考回路和扰动回路稳定。于是,利用劳斯-赫尔维茨判据可得:
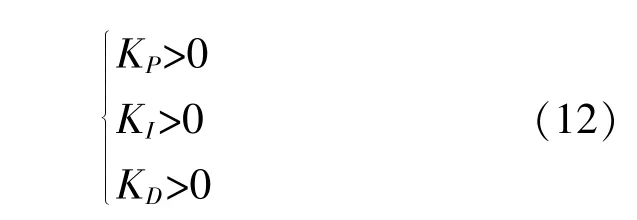
式(12)仅给出回路稳定条件,无法确定和优化参数。为此,本文提出了如下参数确定流程。
①由 式(8)可 知,GC1(s),GC2(s)之 和 为 传 统 的典型PID控制器,因此可优先选定单位加速度信号输入ITAE指标最小的3阶系统[16]确定PID参数,即式(11)中Gyr或Gyd传递函数分母满足:
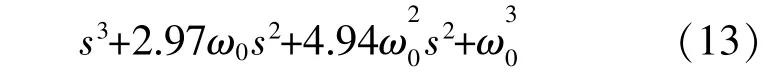
式中:ω0为PLL带宽,取值为70rad/s。
求 得KP,KI,KD系 数,即 可 确 定 抗 干 扰 性 能。
②固 定 上 述 确 定 的KP,KI,KD系 数,再 次 通 过编程变动 α,β参数,求解式(11)中Gyr传递函数在单位加速度信号输入下的ITAE指标最小时的α,β参数,获得表1所示的5个PLL参数。最后回代式(11),求取双自由度PID的闭环传递函数幅值裕度、相角裕度和单位阶跃响应调整时间。
如图5所示:单位阶跃、斜坡、加速度3种扰动信号响应都非常小,单位阶跃响应值约为5.0E-06,而其余两种信号的响应幅值更小1个数量级;衰减时间为0.06s,约3个工频周期。仿真结果证明本文提出的PLL可以有效抑制上述信号扰动。
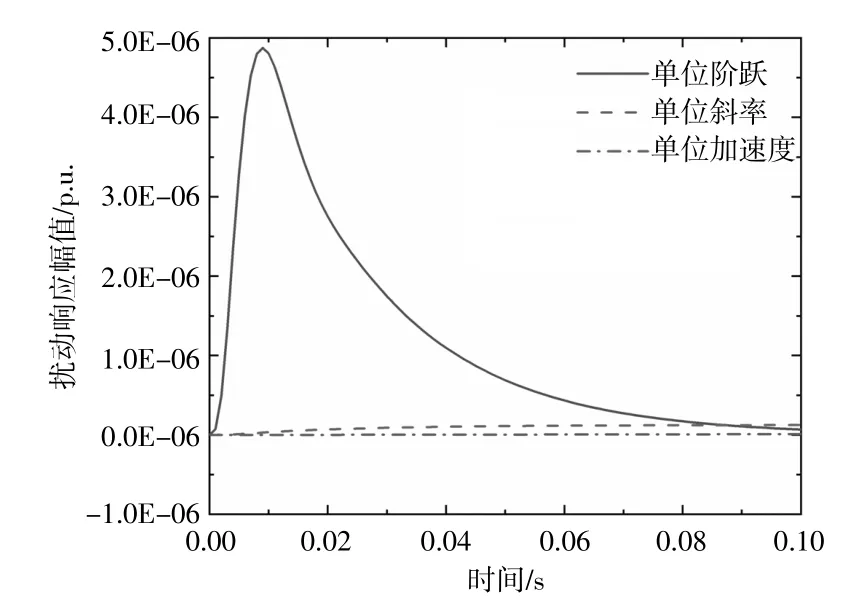
图5 3种扰动信号的响应图Fig.5 The response diagram of three disturbance signals
如图6所示,本文设计的PLL不仅能快速跟踪阶跃指令,过冲很小,而且能够快速无静差跟踪单位斜率上升的斜线,也可以快速无静差跟踪抛物线形式的加速度上升曲线。仿真结果证明本文提出的PLL可以快速无静差跟踪上述信号。
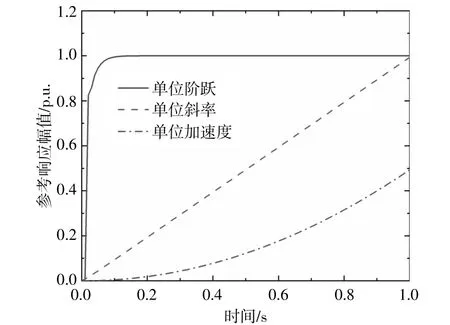
图6 3种参考信号的响应图Fig.6 The response diagram of three reference signals
3 仿真分析
采用如表1所示的参数对所提PLL进行MATLAB/Simulink仿真,为对比PLL的效果,本文将所提PLL输出与tan锁相环、PI-SSRF-PLL结果进行了比较。其中,tan锁相环采用电压正向过零点定位,而本文所提PLL与PI-SSRF-PLL都采用电压正向峰值定位,因此后续图中tan锁相环的输出相位相比其他两种PLL的输出相位提前90°。
3.1 直流分量
如图7所示:在系统电压包含直流分量时,tan锁相环和2DOF-PID III-PLL的输出响应速度快,PI-SSRF-PLL的响应速度最慢;此外,在第一个周期内,相对于tan锁相环,2DOF-PID III-PLL和PI-SSRF-PLL输出相位有明显畸变,第二个周期后畸变消失。因此双自由度PID的微分环节有助于加快响应速度。
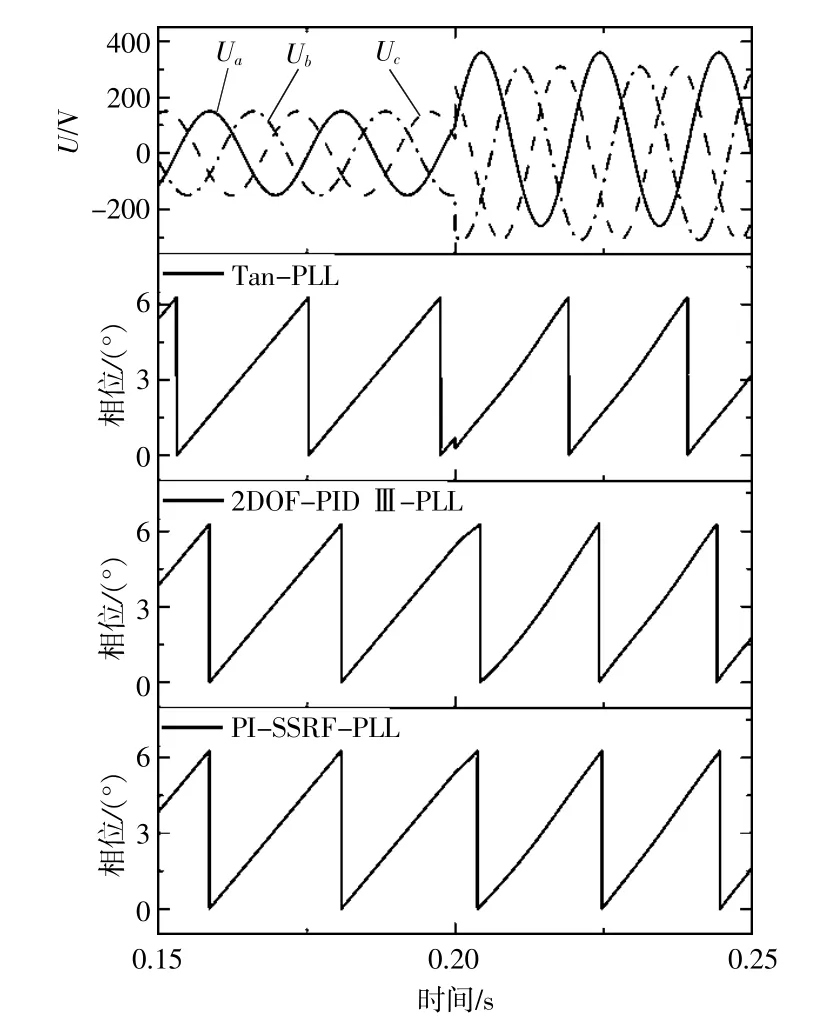
图7 电压包含直流分量的PLL仿真图Fig.7 PLL simulated diagram of voltage including dc component
3.2 谐波(包含不对称负序分量)
如图8所示,在谐波条件下,tan锁相环输出相位畸变非常严重,这种PLL明显不适合于配电网电压包含复杂背景谐波的场合。而PI-SSRFPLL和2DOF-PID III-PLL的响应速度差不多,但2DOF-PID III-PLL输出相位畸变最小,PI-SSRFPLL输出相位则有一定的畸变。
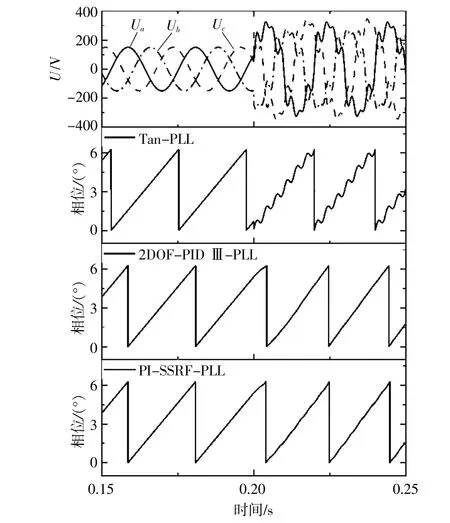
图8 电压包含谐波的锁相环仿真图Fig.8 PLL simulated diagram of voltage including harmonic components
3.3 相位跳变
如图9所示,当电网电压相位突然跳变时,tan锁相环的响应速度最快,2DOF-PID III-PLL的响应速度次之,而基于PI控制SSRF-PLL的响应速度最慢,SSRF-PLL的锁相动态性能相对较差,说明双自由度PID的微分环节有助于加快响应速度。
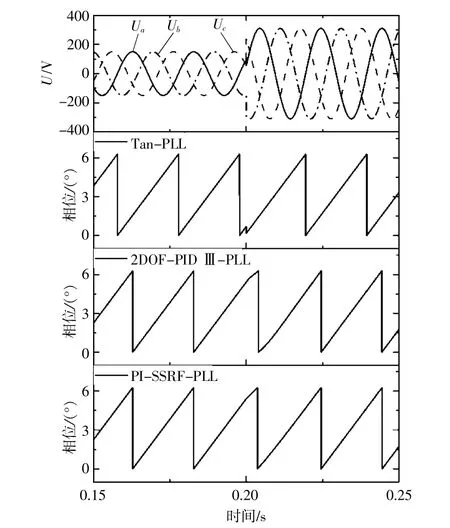
图9 电压相位跳变的锁相环仿真图Fig.9 PLL simulated diagram of voltage phase jump
3.4 频率跳变
如图10所示,当电压频率从50Hz跳变至45Hz时,tan锁相环和2DOF-PID III-PLL的响应速度较快,而PI-SSRF-PLL的响应速度最慢,需要几个周波才能稳定,其锁相动态性能相对较差,说明双自由度PID的微分环节有助于加快响应速度。
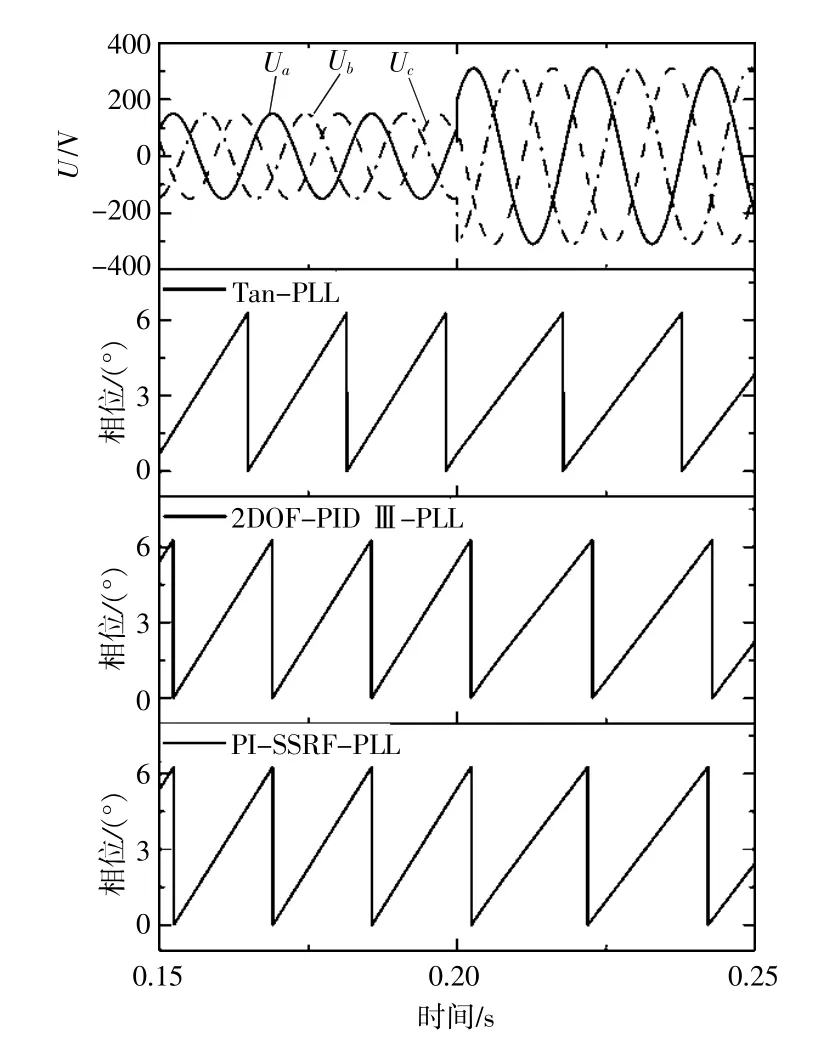
图10 电压频率跳变的锁相环仿真图Fig.10 PLL simulated diagram of voltage frequency jump
3.5 频率加速度变化
如图11所示,当电压频率加速度变化时,tan锁相环和2DOF-PID III-PLL都能较快地跟踪频率加速度变化的电压相位,而PI-SSRF-PLL则不能跟踪相位,出现振荡现象,这种失稳现象与“内模”理论分析吻合,说明传统的PI-SSRF-PLL无法跟踪加速度信号,能力比2DOF-PID III-PLL差。
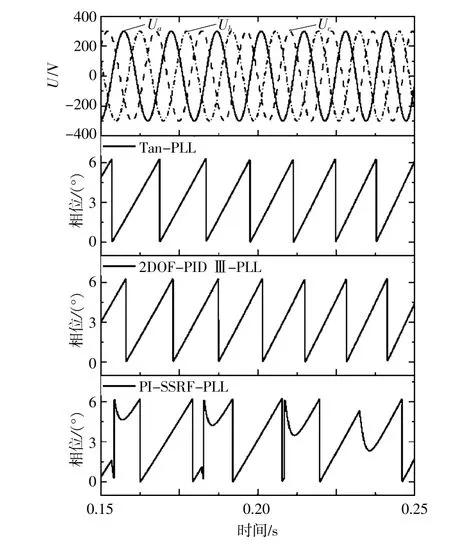
图11 电压频率加速度变化的PLL仿真图Fig.11 PLL simulated diagram of voltage frequency acceleration change
4 结论
根据双自由度PID具有独立优化跟踪与抗干扰能力,以及III型系统可以无静差跟踪加速度信号的特点,本文提出了一种基于双自由度PID补偿的III型PLL技术,给出了该PLL的原理图,推导了其等值模型;然后,根据上述等值模型,提出5个参数设计的方法和优化步骤,给出了详细的参数;最后,通过仿真验证了所提PLL的有效性。研究结论如下。
①基于双自由度PID补偿的PLL,利用5个参数可以独立设计PLL的跟踪和抗干扰性能,同时,根据基于ITAE指标最小达到整体性能的最优化参数。
②III型PLL可以无静差跟踪单位阶跃、斜坡、加速度3种信号,避免传统PI补偿PLL不能跟踪加速度信号的缺陷,解决复杂电网背景下的锁相问题。
③本文所提的PLL技术具有较强的抗干扰能力,针对谐波、直流分量、不对称分量等扰动,2DOF-PID III-PLL完全可以在两个周波内快速地响应并补偿输出准确相位。
④相对于传统PI或PID补偿PLL,本文所提的基于双自由度PID补偿的PLL具有更快的响应速度,充分体现微分环节有助于加快响应速度的能力;同时,通过设置分化系数抑制扰动响应幅值的方法也有助于加大比例系数,进而加快响应速度。

