计及风电随机性的跨区域电-气互联系统分散协调调控

张 瀚，黄 琨，刘凤全，王成福，周万鹏，肖少华

（1.国家电网全球能源互联网集团有限公司，北京 100031；2.国网浙江省电力有限公司嘉兴供电公司，浙江 嘉兴 314033；3.山东大学 电气工程学院，山东 济南 250061）

0 引言

当前各国将能源转型、合作作为能源战略的焦点，旨在促进能源资源优化配置和提高可再生能源消纳水平[1]～[3]。以综合能源系统（Integrated Energy System，IES）[4]概 念 为 依 托，针 对 电、气 互 联系统，国内外学者在可靠性评估[5]、协同规划和运行[6]、能 量 流 分 析[7]，[8]、集 成 建 模 和 随 机 优 化[9]，[10]等方面取得众多成果。

现有成果大多集中在区域型IES中气、电、冷、热等多品类能源系统的转换及耦合机理分析，系统性的跨区域IES研究还很缺乏[11]，[12]。此外，现有成果较少考虑风电随机性对IES运行调控的影响，而利用确定性的单一风电预测场景数据则容易产生较大的计算误差[13]。因此，迫切需要改进调控方法，以应对跨区型IES调控信息不完全互通而影响集中式调控。由于分布式优化理论分解系统整体的优化目标，多个自主体彼此交换部分必要信息，同时进行优化调控以实现有效的协调合作[14]，[15]，因此，该理论与跨 区型IES协调 调控 需求不谋而合。现有文献中分布式优化理论大多用于IES中不同能源类别间的分布式协调[16]，[17]，对于不同能源区域间以及二者同时考虑的研究仍然较少。在算法层面，对偶上升法的可分解性和乘子法的上界收敛属性，在ADMM算法中实现了有机结合，使得该算法在算法收敛性以及解决大规模复杂问题方面具有显著的优势[18]，[19]，因而成为IES分布式协调调控的重要算法。

在相互间信息不完全已知条件下，本文结合ADMM算法提出一种考虑风电出力随机性的CRIEGS分散协调调控策略。该策略可通过分散协调方式应对信息不完全互通所带来的挑战。首先，在联络管线公共节点和耦合元件端口处进行分解撕裂，构建基于ADMM算法的分布式求解框架，并基于拉丁超立方分层采样方法和后向场景削减技术生成典型风电场景。进而，以各个具有耦合关系的能源主体运行成本的期望值最小为目标，利用潘汉德尔修正稳态潮流模型计算天然气系统潮流分布，并考虑网络中各个节点电压、气压安全约束条件等。最后，通过模型线性化方法和变惩罚参数的交替迭代方式，以加快整体求解效率，并通过所搭建的典型算例系统对所提调控策略的可行性与有效性进行验证。

1 CRIEGS协调调控策略

1.1 CRIEGS组成结构及协调特点

本文的CRIEGS由耦合元件、天然气和电力系统组成，典型结构如图1所示。各区域内部的天然气系统与电力系统的双向耦合关系由电转气（Power to Gas，P2G）和 燃 气 机 组（Gas-Fired Unit，GFU）设备构成，区域间的天然气、电力传输以管道、电力线路为纽带。由此，跨区域能源传输与区域内能源交互的内外两层结构已建立成功。

图1 CRIEGS结构示意图Fig.1 Schematic diagram of CRIEGS

跨区协调可分为有上级和无上级协调机构两种类型，分别对应跨省及以下和跨境范围。在我国，跨省电力交易的顺利进行基于统一调度、分级管理模式，在此情况下，上级协调机构可以减少互联区域间信息交互。而在南方电网与东南亚国家的电力交易中，上级协调机构却没有出现，双方通过签订合同，明确电价、电量和送电周期等信息以及联络线技术参数信息，在满足输电协议以及系统安全要求的前提下进行电力输送。此外，天然气系统和电力系统之间也尚未形成上级协调机构，两者长期的独立运营模式属于无上级协调类型。

1.2 分布式求解框架

ADMM算法求解问题的基本形式以及对应的缩放型迭代过程为[21]

式中：x和z分别为优化问题F和G的变量；A，B和c为线性等式约束系数矩阵和向量；λ，μ分别为惩罚参数和对偶向量；k为迭代次数。

在跨区层面分解互联的2个区域，基于天然气、电力分别通过管线和电路线路进行传输的实际情况，利用两者的节点运行状态信息反映能源传输情况，既可方便信息互通，又不影响私密性。因此本文利用节点撕裂方法对联络管线上的公共节点进行分解，如图2所示。

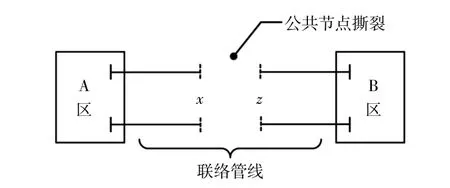
图2 公共节点分解Fig.2 Decomposition of public nodes

当联络管线上没有公共节点时，可以以管线中点作为虚拟节点进行分解。分解后节点及管线两端运行状态变量应满足：

式中：U，θ分别为公共节点的电压幅值和相角；P，Q分别为联络线路传输的有功和无功功率；f为联络管道气流量。

在区域内部，以相互耦合的2个能源类别为分解对象，考虑电力、天然气系统通过耦合元件实现相互转换，将GFU和P2G设备分别看作电力系统和天然气系统的组成元件，进而在GFU和P2G设备的输入端口处进行分解，如图3所示。

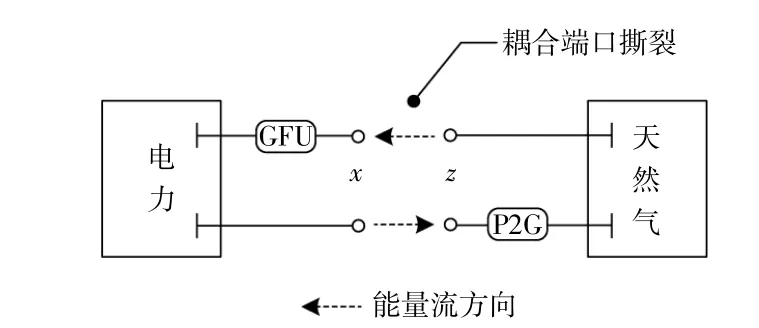
图3 耦合端口分解Fig.3 Decomposition of coupling ports

分解后耦合元件输入端口两端的运行状态变量应满足：

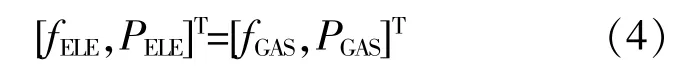
式中：fELE，fGAS分别为GFU耗气量和天然气系统供气量；PGAS，PELE分别为P2G设备耗电量和电力系统供电量。

式（3），（4）为 多 能 系 统 中 耦 合 变 量 的 线 性 等式约束，将其带入式（2）后进行迭代，对系统进行分布式求解。迭代收敛条件满足：

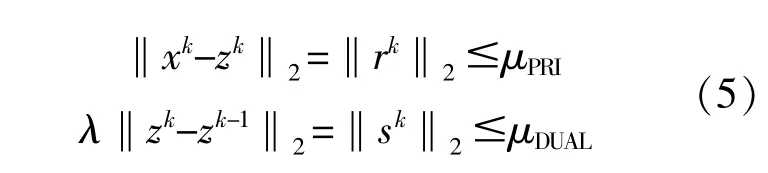
式中：μDUAL，μPRI分别为相对容忍度和绝对容忍度；s，r分别为对偶残差和原始残差。

1.3 场景法

利用多个离散场景表征风电的随机性是一种简单便捷的方法，主要包括场景生成和场景削减2个过程。本文基于拉丁超立方采样（Latin Hypercube Sampling，LHS）[22]方 法 对 日 前 各 时 段 风电预测误差概率分布进行分层采样。假设在任意t时段风电预测出力Pwt的误差服从正态分布N（u，σ2），其 中u为 出 力 期 望，σ为 标 准 差，则 对 应的累积概率分布函数为

将Ft（Pwt）曲线的纵轴均匀分成N等份，其中N为采样数。构造[0，1]上T×N阶随机数矩阵，T为时段数。任意元素 εt，n对应t时段、第n个采样区间的采样点。风电预测出力的采样值由累积概率分布函数的反函数计算得到，即：

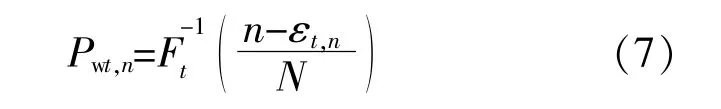
由式（7）即可得到风电预测出力初始场景集，然后结合Gram-Schmidt序列正交化方法[24]对初始场景集进行排列，并利用向后场景削减技术[24]对场景集进行削减，以降低求解规模。

2 日前优化调控

2.1 目标函数

跨区能源合作通常是为了促进送端系统可再生能源消纳、保障受端系统能源供应安全，最终降低系统整体运行成本。因此本文以机组的燃料成本、可控设备的运行成本以及弃风惩罚成本作为目标函数，在保证系统经济运行的前提下，确保风电的最大程度消纳，各个能源区域内部电力主体和天然气主体目标函数的期望E分别为

式 中：S为 场 景 数；ψs为 场 景s的 概 率；PTUi，t，PGFUi，t分别为t时段火电机组和GFU的出力；Pci，t为风电机组弃风量，是风电预测出力与实际出力PWU的 差 值 ；fWEi，t，fP2Gi，t分 别 为 气 源 和P2G设 备 供 气量；下标C，N分别对应不同设备的成本系数和数量。

2.2 约束条件

本文通过添加约束条件来确保系统的功率平衡和安全运行。对于CRIEGS任意节点k的电功率或气流量平衡约束条件为

式 中：Pk，Qk为 节 点k注 入 的 有 功 和 无 功 功 率；fTRi，fPRi各自指代区域间天然气交换量和压缩机耗气量；fLi，PLi为 气 负 荷 和 有 功 电 负 荷 ；fGFUi，PP2Gi分 别为GFU和P2G设备的耗气量和耗电量，并且分别 满 足fGFUi=ηGFUiPGFUi，PP2Gi=ηP2GifP2Gi；wi为 标 识 符 ，天然气供应端取1，接收端取-1；Q其他下标所对应的设备或负荷与P相同。

线性化交流潮流算法在文献[25]，[26]中被应用，本文将其应用于计算节点注入功率，对节点注入功率方程和支路潮流方程进行线性化处理后，可得：

式 中：bki，gki为 各 自 互 电 纳 和 互 电 导；Bki，Gki为 支路ki上的电纳和电导；v为有载调压变压器的变比，此处视为常量并取值为1。

本文使用潘汉德尔修正稳态潮流模型表示气压与远距离输气管道的关系：

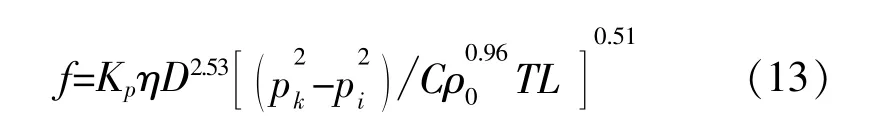
式中：Kp为管道的传输系数；η为管道的输气效率，取值一般为0.9～0.96；T为管道的输气温度；ρ0，C为天然气的相对密度和压缩因子；L，D分别为管道的长度和内径。

先对式（9）左右两边同时进行平方近似处理，得到：

采 用 分 段 线 性 化 方 法[26]，[27]对 式（14）等 号 两 边的二次项进行线性化处理，以y=f2为例，分段线性函数表示为

式中：ϖ为自变量f的分段节点数；fi和yi为第i个分段节点及其对应的函数值；ζi为0～1的连续变量；εi为二进制变量，确保fi左右两端 ζi的值分别 取1和0。

式（14）等号右边气压二次项的线性化形式与式（15）～（18）一 致，只 需 定 义 不 同 的 辅 助 变 量 即可，这里不再赘述。

机组和设备的出力上、下限约束，爬坡约束，管网电压、气压和支路潮流安全约束等安全运行约束条件参考文献[26]。

2.3 迭代求解过程

为进一步加快迭代的收敛速度，本文采用变惩罚参数的迭代方式[29]：

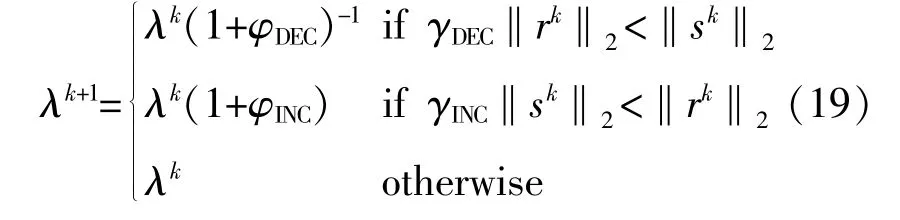
式 中 ：γDEC，γINC为 大 于1常 数 ；φDEC，φINC为 大 于0常数。

本文所提算法迭代过程如图4所示。

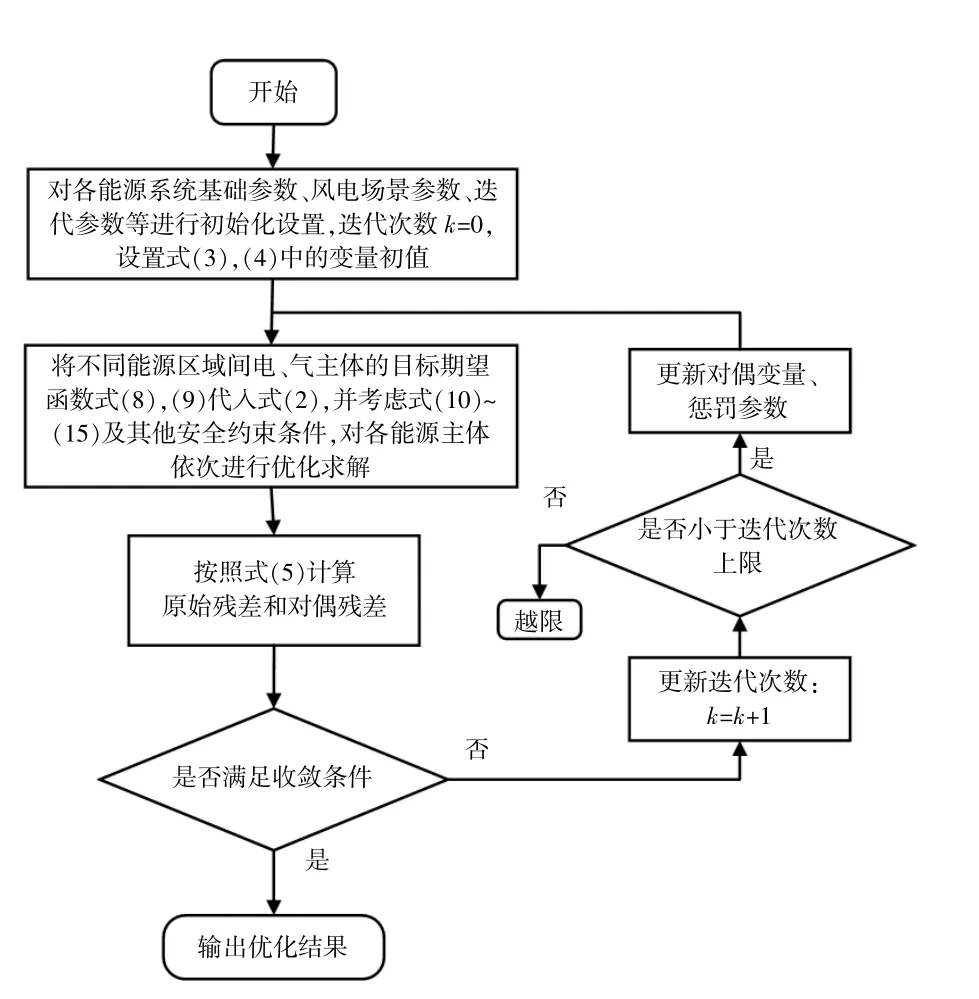
图4 迭代过程Fig.4 Iterative process

3 算例分析

本文构建如图5所示的12bus—12node算例系统进行仿真分析。

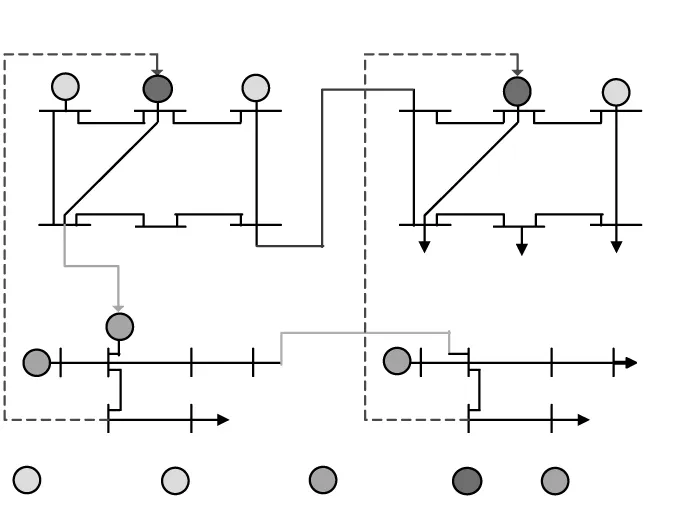
图5 算例结构图Fig.5 Structure of the case

由图5可知，2条联络线路、联络管道将2个具有相同网架结构的电、气互联系统连接起来。各区域中的GFU，P2G设备将6节点天然气系统和6节点电力系统进行耦合。其中，天然气系统为比利 时20节 点 系 统[30]的 第9～12，17和18管 段，电 力系统由标准IEEE6节点系统修改得到。

将风电预测出力的15%作为标准差，取N=1000，利用LHS方法生成24×1000维的风电预测出力场景集，然后进行后向削减为24×10维的场景集，详细数据及场景概率见表1，2。

表1 风电出力情况Table1 Parameters of wind turbines kW

续表1

表2 场景概率分布Table2 Parameters of wind turbines

循环迭代关键参数设置情况见表3。

表3 迭代关键参数Table3 Key iteration parameters

3.1 分散协调调控策略可行性分析

暂不考虑风电随机性，利用表1数据参与系统分散迭代求解。仿真程序在Matlab编写，每次迭代过程调用CPLEX进行求解。经过26次交替迭代过程，程序最终收敛。耦合变量残差以及目标函数值，如图6，7所示。

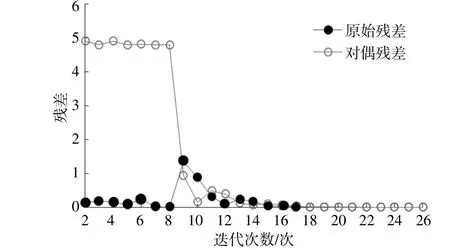
图6 残差变化情况Fig.6 Changes in residuals

由图6可知，在前8次迭代过程中，原始残差的数值明显小于对偶残差，说明按照当前运行状态，部分能源主体可以达到个体运行经济性最优，但是与全局最优状态偏离较大，无法实现全局最优，因此必须改变运行状态。为了不牺牲个体利益，运行状态并没有发生实质性的改变，该结论可从图7的目标函数变化情况得出。由图7可知，前8次迭代完成以后目标函数值缓慢变化，说明各个能源主体运行状态改变幅度较小。从第9～14次迭代过程开始，各个能源主体开始牺牲个体利益以寻找全局最优运行状态。该结论也是由图7目标函数变化情况得出，即目标函数值在第9～14次迭代过程中开始攀升，并逐渐趋于稳定。在这个过程中，原始残差数值先增后减，对偶残差急剧下降，可以表征决策冲突从出现到缓和的变化过程。迭代过程进行到第15次以后，原始残差和对偶残差已基本维持在0.1以下的数值，迭代逐渐逼近最优解。

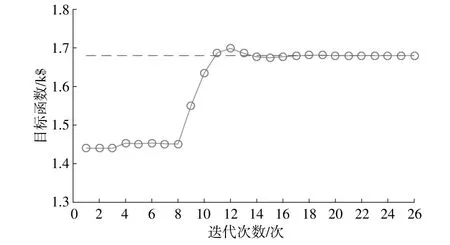
图7 目标函数变化情况Fig.7 Changes in the objective function

3.2 变惩罚参数迭代方式收敛性分析

为验证本文所采用的变惩罚参数的迭代方法在提高交替迭代收敛性方面的作用，将迭代过程中惩罚参数不变（设置为常数1）的方法作为对比方法，将其结果与本文所提变惩罚参数方法的结果进行对比，残差变化情况和其他关键数据对比情况如图8和表4所示。

表4 收敛情况对比Table4 Convergence comparison

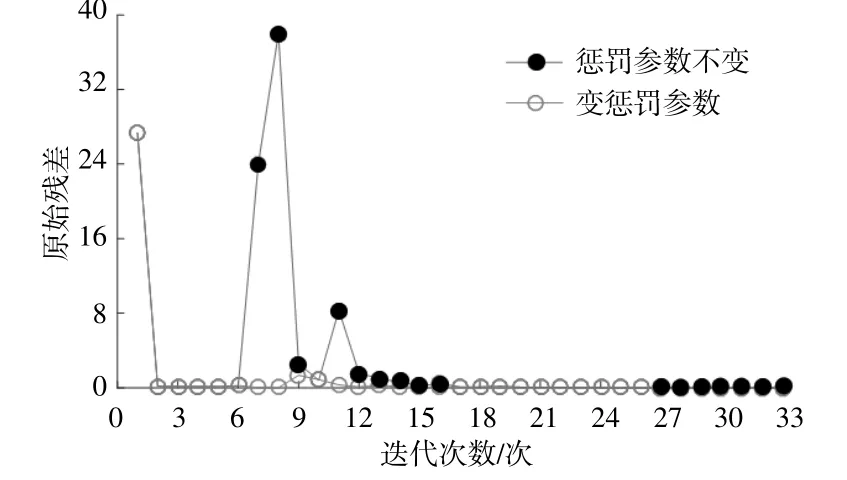
图8 残差变化情况对比Fig.8 Comparison of residual changes

由图8可见，在前6次迭代过程中，两种迭代方式原始残差和对偶残差的数值近似相同，且残差数值相对较大，原因在于边界耦合变量的初始值均设置为1，与最终优化结果的数值相差较大。在第6～12次的迭代过程中，采用惩罚参数不变的更新方式时，原始残差和对偶残差均出现了明显的波动，而采用变惩罚参数的更新方式时残差的波动较小。造成残差波动的原因与增广拉格朗日松弛算法本身特性有关。结合表4以迭代过程中残差逆向（上升）变化为依据，统计的振荡次数可见，变惩罚参数的更新方式可以有效减少残差的波动幅度和次数，有利于残差向着收敛条件变化，从而加快收敛速度。在第12次迭代以后，两种方式下残差已经降低到较低水平，尽管仍然存在振荡，但波动幅度较小。最终，两种迭代方式分别在第33次和第26次迭代以后达到收敛。由于是否采用变惩罚参数的方式，都不会影响每次迭代区域内部各自的求解过程，因此在总的求解时间方面，变惩罚参数方式所减少的求解时间与减少的迭代次数紧密相关。

3.3 场景法及分散协调调控策略有效性分析

通过上述算例结果和分析，已经可以验证本文所提分散协调调控策略的可行性，以及变惩罚参数的迭代更新方式在加快收敛速度等方面的优势。为了进一步分析本文采用的场景法在表征风电出力随机性方面的作用，以及整个分散协调调控策略计算结果的正确性，在前文的基础上，利用表1，2的风电场景数据进行目标函数期望的最优值求解，并假设风电预测出力概率最大的场景3为实际出力，分别计算实际出力和预测出力情况下的目标函数值，并以实际出力的目标函数值为基准计算其他目标函数及其期望的误差，如表5所示。然后，将系统各个能源主体看作一个整体，即将式（8）和式（9）的目标函数整合，将各类约束条件集中罗列，进行统一集中式求解，与分散协调求解结果对比如表6所示。

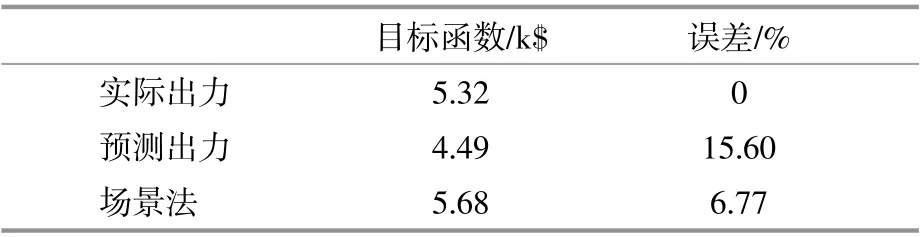
表5 目标函数对比Table5 Comparison of objective functions

表6 与集中式调控结果对比Table6 Comparison with the results of centralized regulation

由表5可见，在假定风电预测出力概率最高的场景为实际出力时，采用单一确定性预测出力的目标函数计算误差较场景法的误差要大，即给优化结果造成的负面影响，同时考虑到场景法较其他解析方法原理和实现方法更加简洁，而且需要的数据较其他抽样方法更少，因此在跨区协调调控中具有很好的适用性。由表6可见，在求解时间方面，分散式调控的求解时间要远远大于集中式调控，这是由于分散式框架中各个能源自主体之间需要时刻交换需要的信息，以同时进行优化，最终迭代求得全局最优解，即本文提出的基于ADMM的分散求解框架本质属于一个大型循环框架，因此，运算的冗余程度提高。这也从侧面体现了本文中调度模型线性化处理的必要性。

4 结论

本文提出一种考虑风电随机性的跨区多能系统分散协调调控策略，基于ADMM分布式优化算法和耦合系统分解方式，实现了CRIEGS的分散协调调控，并以场景法应对单一风电出力预测场景存在较大计算误差的问题。算例结果表明，所提分散协调调控策略能够实现多区、多能源类别间调控信息不能完全互通条件下的协调调控，并通过交替迭代以达到最优运行状态。最终，通过与传统的集中式调控方式进行比对，证明了所提策略的可行性与有效性。