基于Copula理论的风光互补配网经济运行联合配网重构优化

付婷婷，边俐争，李 嫚，甘 辉

（1.郑州电力高等专科学校 电力工程学院，河南 郑州 450000；2.湖南大学电气与信息工程学院，湖南 长沙 410082）

0 引言

风电和光伏的输出功率具有随机性和波动性，在一定程度上两者存在相关性，会对配电网经济运行和网络重构造成一定影响。目前，主要利用Copula函数研究风电和光伏的相关性[1]。文献[2]提出了基于Markov链和Copula理论的风光联合输出功率时间序列模拟生成方法。除此之外，针对动态风功率建模，主要是以Copula相关性进行的动 态 模 拟[3]，[4]。

在配电网络运行优化方面，文献[5]分析了多类型分布式电源接入下的低压交流与直流配电网运行经济性。文献[6]针对配电网自动化系统的经济运行及优化配置进行了分析。文献[7]计及了多类型需求响应的孤岛型微能源网经济运行。文献[8]探究了考虑分布式电源和电动汽车不确定性的双层动态配网重构。

以上文献说明，配网运行的优化离不开对内部电源的出力预测、调度优化，而风电和光伏是实现碳减排的重要手段，其出力方式呈现不确定性和波动性，因而需要在配网区域内实现对这类能源的精准预测，再将其出力与配网内其他元素结合进行优化分析。另外，风速和光照强度的相关性对于这类能源的优化运行影响应进一步明确，尤其是针对相关性出力的影响。

目前对于这类优化问题的优化求解方法分为分析法、启发式方法、智能人工算法等[9]。启发式算法在求解这类问题时应用广泛，主要包括对偶半 定 规 划[10]、粒 子 群（MOPSO）算 法[11]、差 分 进 化 算法[12]等。启发式算法较成熟，能够在一般条件下得到最优解。

综上所述，在目前已有研究中，针对风光互补下的配网经济运行已经较为详细，但并未将配网重构与网络经济运行相结合，同时在风光互补发电方面也没有进一步分析。本文考虑风光互补、配网经济运行、配网重构三者有机结合，将风电和光伏的出力以互补的形式进一步明确，满足经济运行要求和配网重构要求。

1 基于Copula理论的风光互补发电系统联合出力

1.1 风电光伏输出功率

风力发电机的输出功率与风速大小有着密切的 关 系，如 式（1）所 示。

式中：Pwind为风力发电机的有功输出功率；Pr为其额 定 有 功 输 出 功 率；v，vi，vr，vo，voc，vh分 别 为 实 际风速、切入风速、额定风速、切出风速、切出风速上限、实际出力风速。

在实际工程中，光伏发电的输出功率与光照强度间的数学表达式为

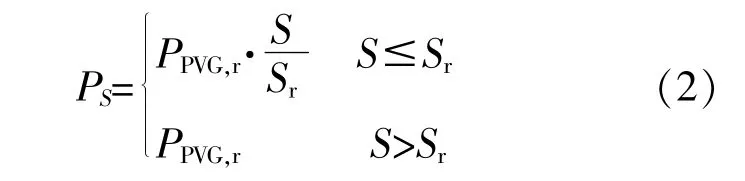
式 中：Sr为 光 伏 发 电 机 的 额 定 光 照 面 积；PPVG，r为其额定输出功率。

其中风速按照双参数Weibull分布、光照辐射强度按照Beta分布进行模拟，限于篇幅在此不做展开。

1.2 Copula相关性度量

相关性度量用以表示随机变量之间的变化关系，主要有Pearson相关系数 ρ，Kendall秩相关系数 τ及Spearman秩相关系数 ρs。本文两组随机变量为风电场和光伏电站的输出功率，两者受时间、地点等因素影响，具有明显的不确定性和波动性，并且两者之间无线性相关关系，也无固定分布情况，所以Pearson相关系数以及Kendall相关系数并不适用。因此，本文选用Spearman秩相关系数表征风光随机变量的相关性。Spearman秩相关系数描述随机变量等级间的相关性，首先将随机变量的样本从小到大排列，然后计算其各自的秩次，再基于随机变量的秩次计算相关性[5]。

Spearman秩相关系数为

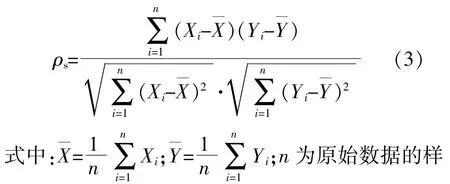
本 数；Xi，Yi各 为 两 组 样 本。

1.3 Copula相关性联合出力

为说明Copula相关性分析方法，选择某两地历史数据进行分析。计算本文所述Spearman秩相关系数，描述两者相关性，12个月的结果如表1所示。

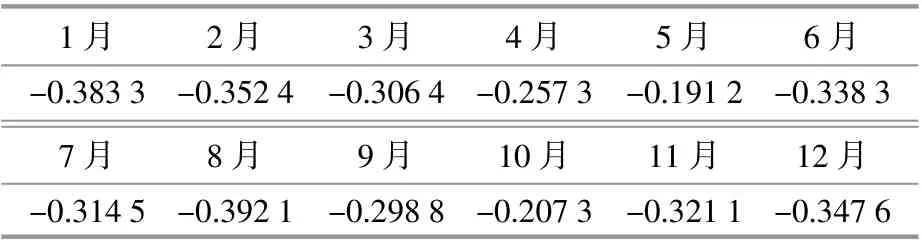
表1 Spearman秩相关系数Table1 Spearman correlation coefficient

其中：相关系数为正值，表示风电场和光伏电站输出功率数据是正相关；相关系数为负值，表示风电场和光伏电站输出功率数据是负相关，即互补关系。从表1可得，同一地区风电场和光伏电站输出功率的相关系数为-0.20～-0.40，这说明它们之间存在负相关性。

风光输出功率具有负相关性，因此需要选择合适的Copula函数作为风光联合概率分布的连续函数。由风速、光照数据得到风电、光伏输出功率数据，并将其计算成出力率，进行归一处理，以风光电源输出功率作为随机变量，得到其边缘分布。本文根据风电、光伏的特点，选取Frank-Copula函数作为二者联合概率分布的连续函数，如表2所示。

表2 Frank-Copula函数Table2 Frank-Copula function

风光互补发电系统的输出功率即为风光电源输出功率之和。求取风光互补发电系统出力的概率分布可以转化为求取风光电源输出功率的联合概率分布。具体步骤如下。

①对风光出力率P1，P2的样本进行核密度估计，得 到fWT（P1），fPV（P2）。

②对fWT（P1），fPV（P2）进 行 积 分，得 到 风 电 和 光伏 出 力 的 累 积 概 率 分 布，即FWT（P1），FPV（P2）。

③计算风光电站出力的Spearman秩相关系数，利用秩相关系数与Frank Copula函数之间的关系，求解Frank Copula函数模型中的α参数。

④根据Copula理论，得到随机变量P1，P2的联合概率密度，表达式如下：

式 中：u=FWT（P1）；v=FPV（P2）。

⑤对风光出力的联合概率密度函数h（P1，P2）进行积分[6]，得到风光互补系统的联合出力Ph（X）。

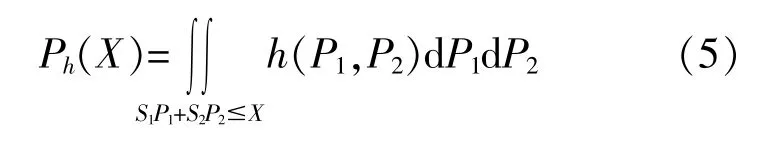
由Ph（X）形成满足风光电站的出力时刻表，此表既包含了风光出力的随机性，也包含两者之间的相关性。不再将风电、光伏的出力作为两个单独的随机变量，而是考虑风光出力相关性的情况下对配电网的经济运行进行研究，使最终研究结果更贴近实际。

2 配网经济运行联合配网重构优化模型

2.1 风光互补相关性的考虑

在配网重构模型中，风光相关性主要体现在网络失负荷惩罚成本和购电成本。相关性越强，风电和光伏的互补优势就越明显，在同等条件下系统失负荷成本应该有所下降，同时向大电网购电的成本也会下降。

另外，由于在风光互补计算中考虑了风速、光照强度的不确定性，在重构模型中不再重复考虑该不确定性，而直接利用式（5）得到的联合出力作为模型的输入进行优化。

本文由Frank-Copula联合分布函数根据联合概率分布形成风电场和光伏电站出力时刻表，以此作为失负荷惩罚成本以及购电成本的计算依据。

2.2 配网重构优化目标函数

①有功网损最小

第一个目标函数使得所有支路的有功网损之和最小，具体表达式如下：

式中：PL为网络总有功网损，kW；Ib为支路b的电流，A；Rb为 支 路b的 电 阻，Ω；Nb为 支 路 数。

②年运行成本最小

配网运行中，主要的运行成本包括分布式电源装机成本、维护成本和损耗成本。第二个目标函数为

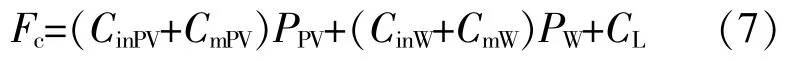
式中：CinPV和CinW分别为光伏和风机的装机成本，$；CmPV和CmW分别为光伏和风机的维护成本，$；PPV和PW分别为光伏和风机的出力，kW；CL为年有功损耗成本，$。

年有功损耗成本利用峰时段负荷进行计算，具体计算式如下：

式 中：EC为 单 位 有 功 损 耗 成 本，$/（kW·h）；EL为 有功 损 耗 值，kW；PLpic为 峰 荷 总 有 功 损 耗，kW；Fls为给定时段（1a）有功损耗因子。

③向上级电网购电成本

第三个目标函数为

式中：Tmax为最大负荷利用小时数；PΣl为整个配网系统中的负荷总量；n为配网系统中电源类型种类数；max为第i种类型电源的最大发电利用小时数；S为接入的第i种类型电源总容量；Cpu为向上级电网购电单位电量价格。

④失负荷惩罚成本

式中：Estop为供电不足被迫停运的负荷量；Psys为系统中规定的由接入电源供电的负荷量；PS为接入电源的实际有功出力量。

2.3 配网重构优化约束条件

①功率平衡约束

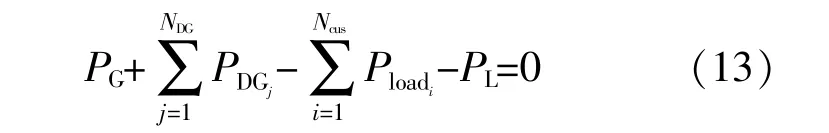
式中：PG为传统机组有功出力，kW；Ploadi为节点i的 负 荷，kW；Ncus为 负 荷 节 点 数 目；PDGj为 第j个DG机组出力，kW；NDG为DG数目。

②电压约束

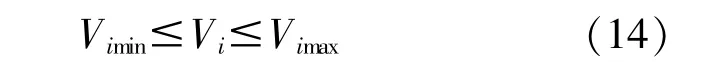
式 中：Vi为 节 点 电 压，pu；Vimax，Vimin分 别 为 节 点i电 压 上、下 限，pu。

③支路电流约束

④DG容量限制

DG发电占配网总有功负荷的10%～60%。

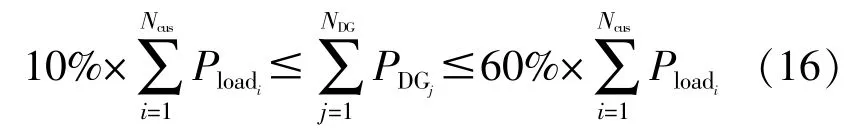
⑤网络拓扑结构约束

配网是闭环设计、开环运行的，因此应当在运行中保持网络结构为辐射状。根据图论的相关理论，辐射状的配电网应当满足：

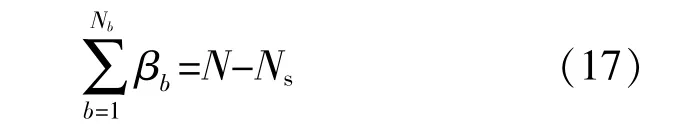
式中：βb为二进制变量；0表示支路b断开，1表示支路b闭合；N为网络中节点总数；Ns为网络中松弛节点数。

3 改进帕累托强度算法求解

本文含有多目标函数，对于多目标优化问题，常用的方法是将多目标问题转化为单目标进行处理，但这样得到的结果只是一种权重下的最优解，对于权重指标较为敏感。进化算法在代与代之间进行全局搜索，最终得到帕累托最优解。强度帕累托 进 化 算 法2（Strength Pareto Evolutionary Algorithm2，SPEA2）在求解高维多目标优化问题时具有优势，因此本文利用SPEA2进行求解。求解过程如下。

①生成初始种群

SPEA2首先要生成随机某代的某一个体（染色体）的初始种群P0，以及一个外部存档At，即最优个体在算法的选择过程中在该存档中复制。一个个体表示一个优化问题的可能解。针对本模型的具体情况，一个个体由配网可能的辐射状拓扑结构和分布式电源机组的联合出力构成。算法求解时，需要利用图论的相关理论以及深度优先搜索 算 法（Depth First Search，DFS）来 评 估 生 成 的 配电网拓扑的可行性。

本文的基因编码如下：

式中：indi为种群中的个体i；s1s2…snop为常开开关集；loc1loc2…locNDG为DG的节点位置；PDG1PDG2…PDGNDG为 联 合 出 力 。

②适应度赋值

计算种群中每个个体的目标函数值，并根据其适应度进行选择。在SPEA2中，适应度赋值是通过“支配”关系来确定的，即Pareto最优的概念。

③环境选择

SPEA2的环境选择机制中，最适应个体被复制到一个大小固定的外部存档中，以防在交叉和变异过程中丢失。该存档通过加入新的非支配个体直到达到存档的上限，而在一代一代之间不断更新。

④基因重组

本文中，网络重构的编码为开关变量，其非可行重构一般是孤岛、非辐射状结构。为了避免这种缺陷，将生成树理论应用于交叉和变异中，保证得到的配网结构是辐射状的。本文对SPEA2的改进如下。

首先，在交叉过程中使用最小生成树之克鲁斯卡尔（Kruskal）算法，即通过交换一个或若干两个配网内的树支来得到下一代或者新的配网辐射状结构，具体的定义如下：

令U和T为图G的两个生成树，a为满足a∈U的树支，并且存在b∈T的树支，相应地，Ua-b为图G的生成树。

变异算子通过随机选择一个断开支路与相同的生成树中的另一树支交换，保持其辐射状结构。经过复制过程后，根据约束条件，得到新的个体，只有其中的可行解才能继续构成下一代的种群。经过上述过程的反复操作，达到满足适应度值的固定规模种群数。

最终，基于模糊集的决策理论可以用来选择Pareto解集中的最优折中解。

SPEA2流程如图1所示。

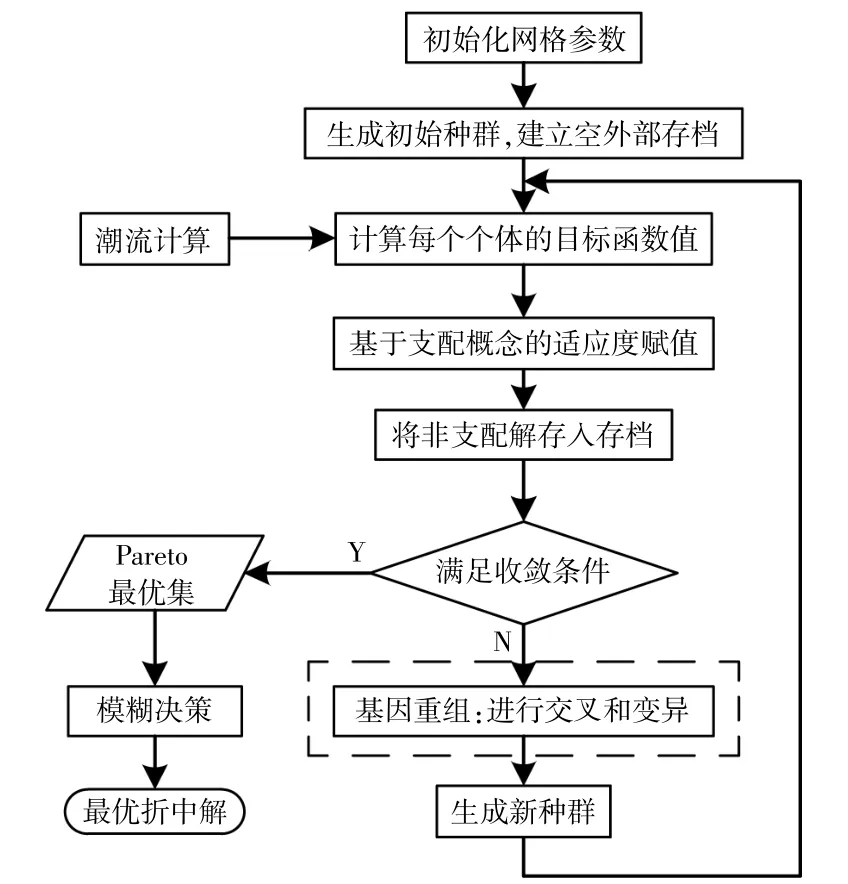
图1 算法流程Fig.1 Flow chart of algorithm

4 算例分析

4.1 系统说明

本文选取IEEE33节点系统进行仿真分析，仿真环境为MATLAB2014b，如图2所示。IEEE33配电系统的电压等级为12.66kV，总负荷为5064+j2547kVA，三相功率基准值取10MVA。该系统具有1个电源、5条联络开关支路、32条支路和33个节点。风力发电机待选安装节点为3，7，8；光 伏 发 电 站 待 选 安 装 节 点 为5，12，17，接 入节点容量限值均为180kW。单台电源的额定容量取25kW。在计算网络损耗时，接入配电网的机组为PQ节点。

图2 IEEE33节点系统接线图Fig.2 IEEE33bus feeder

本文选择的机组费用参数如表3所示。

表3 费用参数Table3 Tariffs list

①风机模型

风力发电机的额定风速vn=15m/s，切入风速vi=4m/s，切 出 风 速vo=21m/s。Weibull分 布 下 的 形状因子k=2.30，尺度因子c=8.92。

②光伏模型

光伏发电机的额定光照强度Sr=1000W/m2，Beta分 布 下 的 尺 度 因 子α=0.85，β=0.85。

考虑到同一地区的风力发电和光伏发电具有相关性，采用Frank-Copula函数拟合两者的出力。并考虑实际配网所处地区的实际情况，选择该地区一年Spearman秩相关系数的平均值为-0.31。

4.2结果分析

根据本文建立的风机-光伏联合出力模型，得到当地风机和光伏电站有功出力曲线，如图3，4所示。图中风机和光伏的装机容量均统一为单位容量20kW。

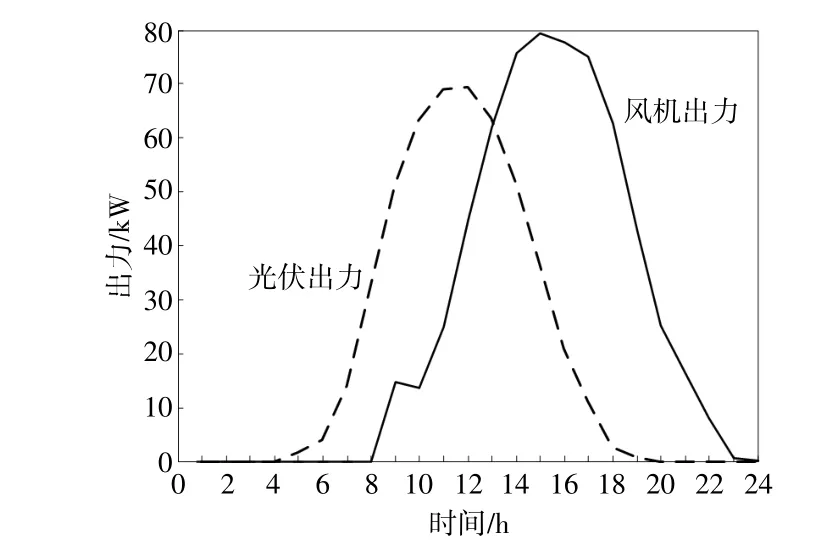
图3 风机和光伏出力Fig.3 Wind and Solar generation curve

图4 负荷曲线Fig.4 Demand curve

针对考虑相关性和不考虑相关性的情景进行对比，结果如表4所示。

表4 电源优化结果Table4 Results of power optimization

表5为配电网投资成本。由表5可以看出，风光出力相关性主要影响了失负荷惩罚成本和购电成本。方案一中失负荷惩罚成本为8.8706万元，方案二为12.6076万元。两种方案下，风机和光伏的间歇性电源的数量相差无几，而失负荷惩罚成本却相差3.737万元。这是由于方案一考虑了风光出力的相关性，且两者是负相关即互补关系，使得系统的失负荷成本有明显下降。

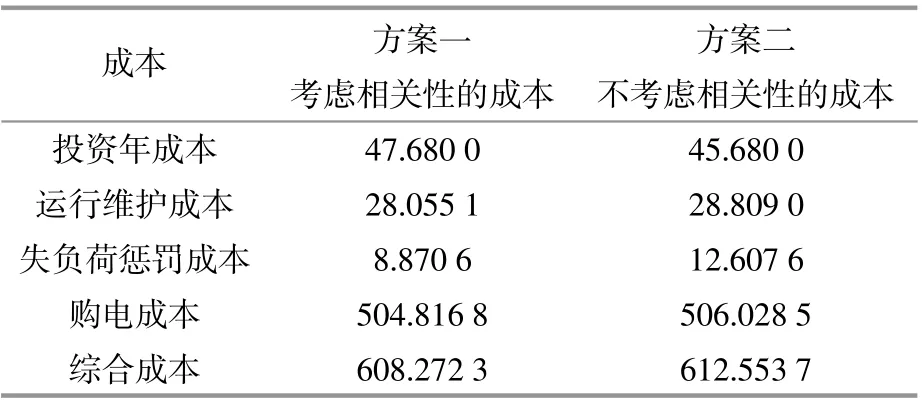
表5 配电网投资成本Table5 Investment cost 万元

日内配网重构的求解结果如表6所示。表中sXX表示联络开关编号。

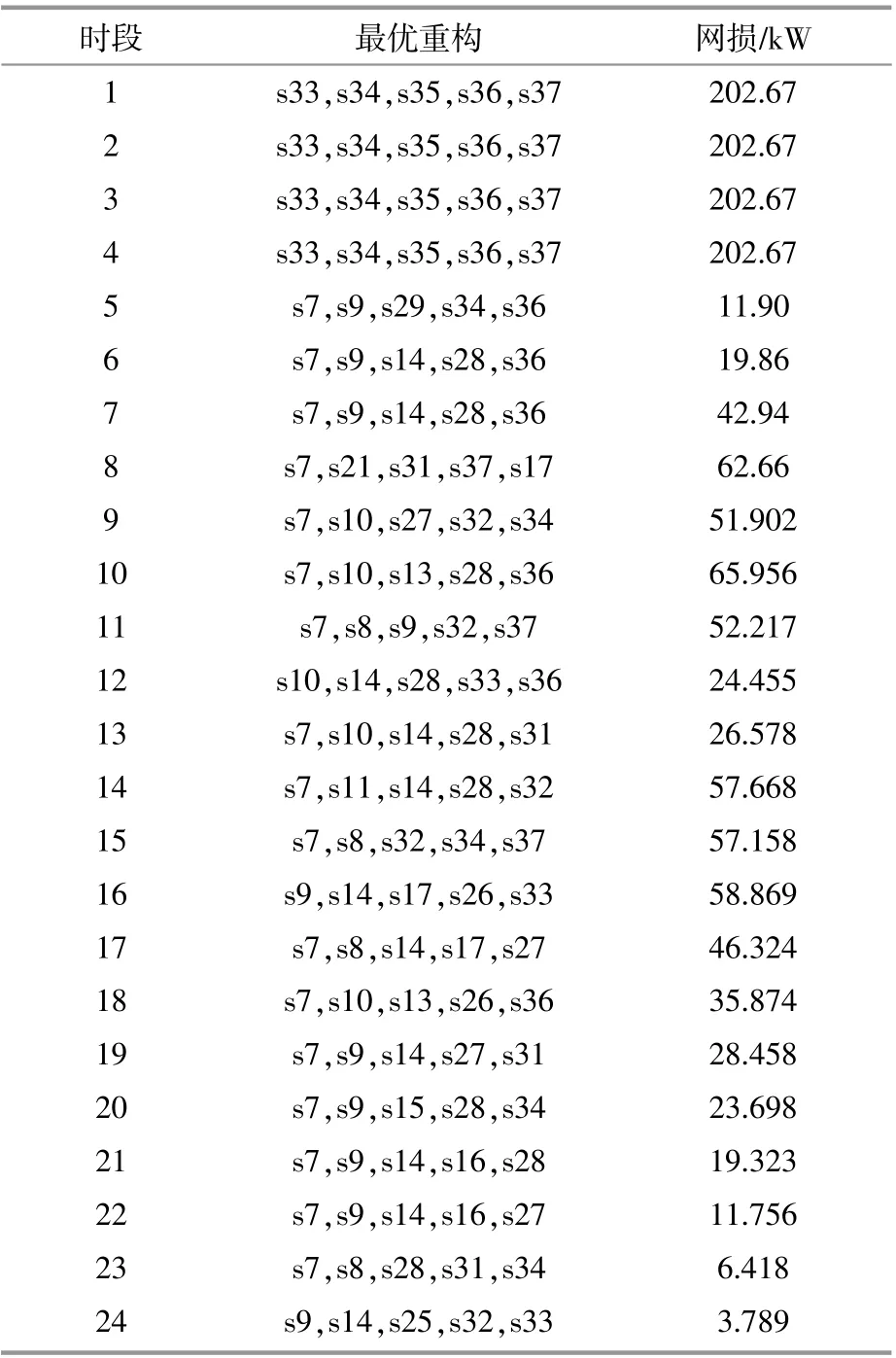
表6 日内配网重构求解结果Table6 Network reconfiguration results

在利用改进的SPEA2对配网重构和分布式电源选址定容联合优化求解后，可以得到配网的最优拓扑，同时得到分布式电源的最优位置和最佳配置容量，而不需要单独分开计算，这对于电网的规划与运行是十分有意义的。

5 结论

本文提出了风光互补条件下配网经济运行以及配网重构优化模型，通过仿真模型分析得到如下结论。

①风电以及光伏电源输出功率具有负相关性，系数绝对值越高，表明负相关性越明显，联合出力分布能够有效提升机组输出功率在计算过程中的准确性。

②通过建立多目标优化模型，考虑电网运行成本、网络损耗，能够同时求解配电网络重构结果，本文提出的改进SPEA2能够获得更好的收敛性。仿真分析结果表明，考虑风电相关性后，失负荷惩罚成本大幅下降，总成本以及购电成本相差不大。