计及UPFC的含新能源电网静态电压稳定性分析

曹 帅，沈凤杰，葛亚明，闫朝阳，钱威臣，马道广

（1.国网江苏省电力有限公司，江苏 南京 210000；2.国电南瑞科技股份有限公司，江苏 南京 211106；3.南京邮电大学 先进技术研究院，江苏 南京 210023）

0 引言

目前，以新能源为主体的新型电力系统采用超高压远距离输电和区域电网互联，在“西电东送、南北互供、全国联网”的规划下得到广泛应用[1]；同时，大规模新能源呈现高比例并网的发展趋势，截至2020年底，我国新能源发电装机比例占总装机规模的42.4%，装机容量达到9.3亿kW，开发规模稳居世界第一[2]，[3]。在大规模新能源发电场景下，解决新能源发电的随机特性给电力系统稳定运行带来的挑战，是当前研究人员重点关注的问题[4]，[5]，其中静态电压稳定问题尤为显著。

针对新能源并入电网后的静态电压稳定问题，国内外学者已进行了大量的深入研究，提出了相应的静态电压稳定性指标。传统静态电压稳定分析一般以潮流计算为基础，寻找静态电压稳定临界点，计算得到当前系统节点的电压稳定裕度，常用的方法有连续潮流法、直接法、非线性规划法[6]。文献[7]，[8]基于节点P-V曲线和Q-V曲线，将临界稳定运行的节点电压变化值和无功功率变化值的加权和作为综合电压稳定指标，评估内部负荷变化时电力系统的电压稳定性。文献[9]，[10]按照简化系统思路和分析配电网的单条线路模型，在潮流计算的基础上提出配电网静态电压稳定指标。但现有的静态电压稳定指标大多根据确定的模型进行设计，忽略了负荷波动、新能源发电不确定性等因素，难以充分反映当电力系统受到扰动后整体的运行状态，限制了静态电压稳定指标的通用性。

伴随着电力电子器件的发展，柔性交流输电技 术（Flexible AC Transmission System，FACTS）在改善静态电压稳定性方面的研究更加深入[11]。文献[12]分析了风电场并入电网对系统静态电压稳定性的影响，并提出通过安装FACTS装置的策略改善系统薄弱线路潮流，增强电压稳定性。上述文献中没有将FACTS装置与电力系统潮流计算方程结合提出新的电压稳定指标，并且未考虑新能源电网配置FACTS装置后对电力系统安全稳定运行性的提升。统一潮流控制器（Unified Power Flow Controller，UPFC）作为目前先进的柔性交流输电装置之一[13]，[14]，为电网的安全运行提供了一种电压支撑和功率调节的方法，UPFC通过调节线路潮流，有效缓解了高比例新能源接入电网后对系统安全运行所带来的危害[15]。

本文提出利用UPFC提升新能源电网静态电压稳定性的方案。首先通过功率注入法建立UPFC装置的等效模型，得到基于UPFC的潮流计算方程；然后利用潮流计算方程提出相应的系统静态电压稳定性指标，定量分析不同容量新能源并入电网后配置UPFC对当前电力系统薄弱节点静态电压的提升；最后通过仿真验证本文所提出的静态电压稳定性方案的有效性和准确性。

1 UPFC的等效功率注入模型

UPFC是由两个共用直流侧电容的背对背式电压源换流器构成。其中：一个变流器直接通过变压器串联接入系统，向系统注入幅值与相角可任意调节的电压，以此调节线路潮流，在装置内可等效成一个串联电压源UT；另外一个变流器通过并联变压器漏抗接入系统，该换流器可以通过并联变压器向系统吸收或者注入无功功率，在装置内可等效成一个串联电流源Ish，并且向串联侧变流器提供有功功率支撑，使装置与系统之间总的有功功率交换为零，从而维持直流侧两端电容电压的稳定。

图1为UPFC的等效电路图，其中在线路i～j的节点i处加入UPFC装置，并联侧变流器可将电流源Ish分解成Ui同向的有功电流分量It以及与Ui成正交的无功电流分量Iq。

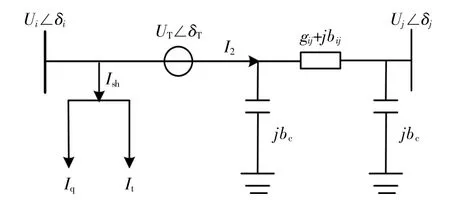
图1 UPFC的等效电路图Fig.1 Equivalent circuit of UPFC

利用等效功率法将UPFC转移到输电线路的两侧节点上，根据UPFC的等效电路图可以计算得出i，j节点处的注入功率平衡方程。

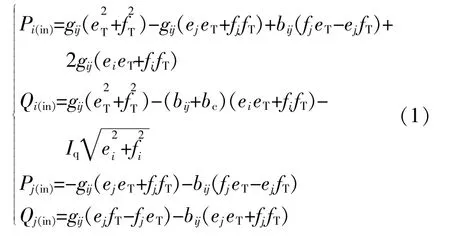
式中：e，f分别为系统注入电压的实部和虚部；eT，fT分别为等效电压源的实部和虚部，即eT=UT·cos（δT），fT=UTsin（δT）；bc，bij，gij分 别 为 输 电 线 路 上i～j的电纳、接地电纳和电导。

2 含UPFC的系统静态电压评估

2.1 电力系统潮流方程

对于任何复杂的电力系统，其系统都可以简化为共包含n个节点、m-1个PQ节点，n-m个PV节点和一个平衡节点，则潮流平衡方程以及简化后的潮流平衡方程可以分别表示为

式中：ΔPi为系统第i个节点有功注入功率量；ΔQi为系统第i个节点无功注入功率量；Ui为系统第i个PV节 点 电 压 值；Gij，Bij分 别 为i～j支 路 导 纳 的实部和虚部；H，N，J，L分别为潮流系统第i个节点功率状态矩阵；Δθ为i～j支路的变化角度；ΔU为系统i～j支路的变化电压值。

2.2 含UPFC的潮流计算方程

将UPFC配置在线路i～j的节点i侧，并对配置UPFC所在线路两端的潮流方程进行修改，其他节点潮流方程保持不变。修改后的潮流方程为

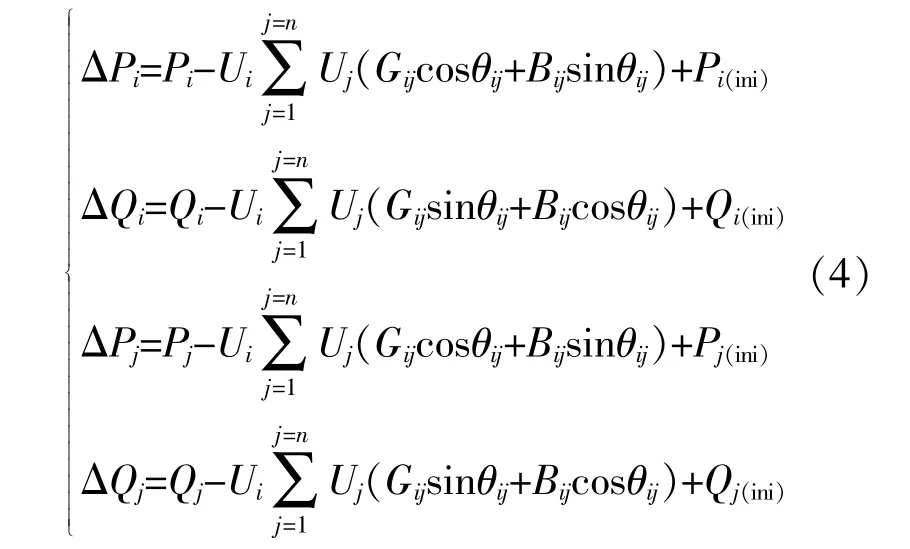
式 中 ：Pi（ini），Qi（ini），Pj（ini），Qj（ini）分 别 为UPFC注 入 系 统节点i，j的有功和无功功率。

2.3 电力系统静态电压稳定指标

对于任何的电力系统来说，其简化后的支路模型如图2所示。

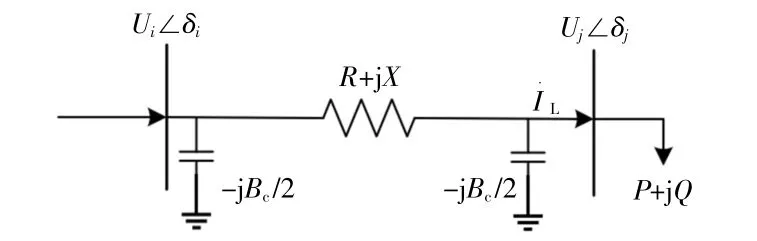
图2 输电网简化模型图Fig.2 A simplified model diagram of the transmission network

图中：支路i节点首端电压为Ui，末端节点电压 为Uj；R+jX为 支 路 阻 抗；Bc为 对 地 导 纳；P，Q分别为支路末端的有功、无功功率。

从而可得相应的电压方程为

故节点j电压稳定的条件是Uj有实数解。系统在正常稳定运行的情况下时，Uj有两个正实根，其中，较大的根是一个稳定的解，另外一个较小的根是不稳定的解，当系统处于临界稳定时两个根达到同一个临界电压U，此时Δ=（b2-4ac）=0[9]。因此可得：

则曲 线 上的 点 为Qcr和Pcr。设x=Q，y=P，有：

图3是以线路无功功率和有功功率为坐标的

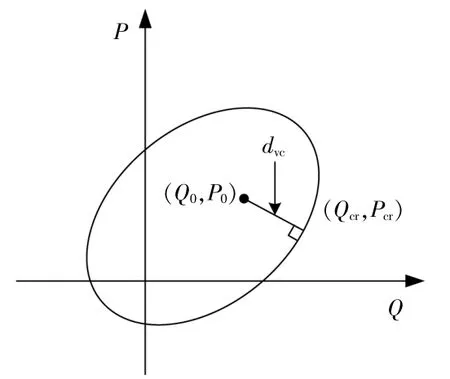
图3 安全稳定运行曲线Fig.3 Safe and stable operation curve

电压安全稳定运行曲线，（x1，y1）为系统的运行状态，本文的电压稳定安全裕度可以表示为

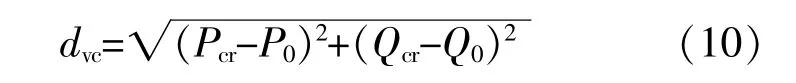
如图3所示，UPFC装置通过调节线路潮流的方式改善系统静态电压稳定性。线路末端负荷节点j的电压稳定值可表示为

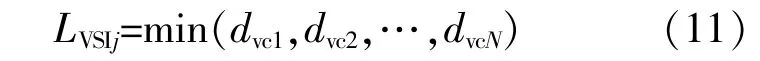
式中：N为系统中以j为节点末端的支路总数。

电网整体电压稳定性的强弱与节点电压稳定裕度成正比，以节点为末端的支路处于稳定裕度为0，即支路电压稳定性处于临界状态，越过临界运行状态将会在此节点出现电压崩溃的现象，同时丢失输电线路原本的平衡节点。系统在不同运行状态下的最小节点电压稳定裕度被定义为系统最薄弱节点，此节点安全裕度的大小能体现系统整体的静态电压稳定性，即：

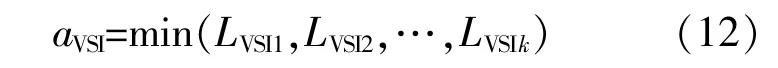
式中：k为系统中负荷节点的个数。

当系统由于负荷的增长面临节点电压崩溃时，薄弱节点达到临界运行点的概率最大。

3 算例分析

为研究分析安装UPFC装置对新能源电网静态电压稳定性的影响，设定UPFC的容量为500 kV。本文通过IEEE-RTS79节点系统（图4）对所提出的使用UPFC提升新能源电网静态电压稳定性方案进行仿真验证。

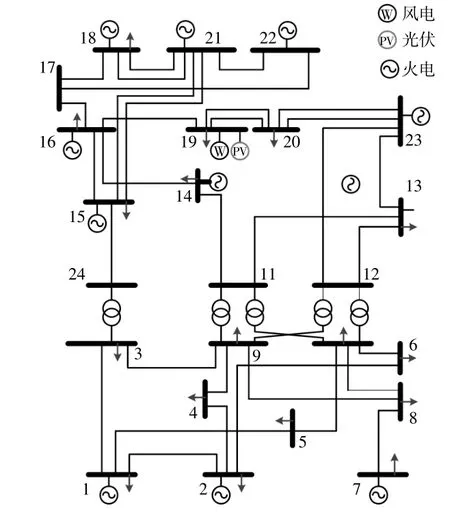
图4 IEEE-RTS79系统Fig.4 IEEE-RTS79systems

3.1 新能源对系统静态电压的影响

图5为本文所使用的IEEE-RTS79系统在初始状态下各节点LVSIj的值。由图可知，19节点在初始运行状态下的LVSIj为0.3310，可认为系统在该节点的电压安全稳定裕度最小，在整个系统中处于最薄弱位置。伴随着新能源并入电网的负荷逐步增加，该节点发生电压崩溃的概率最大，危及整体电网的安全稳定运行。

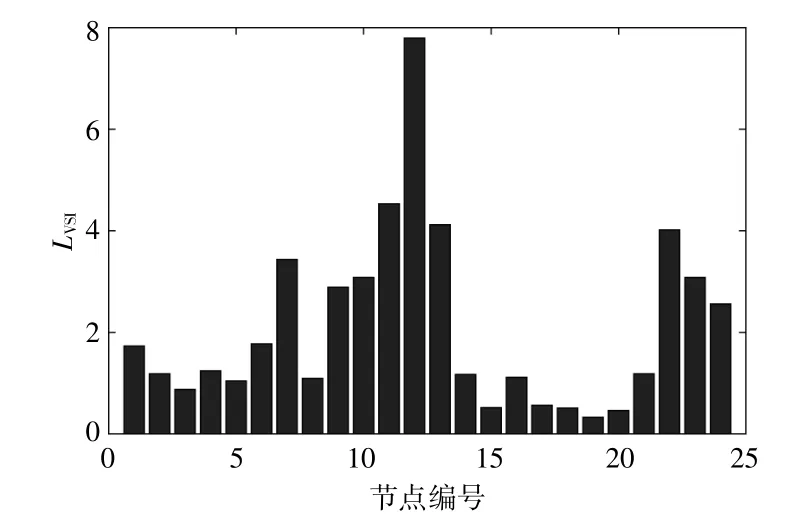
图5 初始状态下的各节点静态电压稳定值Fig.5 Static voltage stability value of each node in initial state

随着新能源装机比例逐步增大，系统薄弱节点的电压幅值均有所下降，如图6所示，当新能源装机容量达到800MW时，其中薄弱节点19的变化最为明显，系统电压指标值aVSI下降了0.827 p.u.。由此可见，节点19对新能源规模变化的反应最敏感，新能源的扰动会造成节点电压的显著变化。在新能源增长过程中，该节点的安全稳定范围最小，系统电压从此处节点崩溃的概率也更大，因此取初始状态下的19号节点的LVSI值为系统电压稳定指标aVSI，能够更好地反映整个系统的电压稳定值。

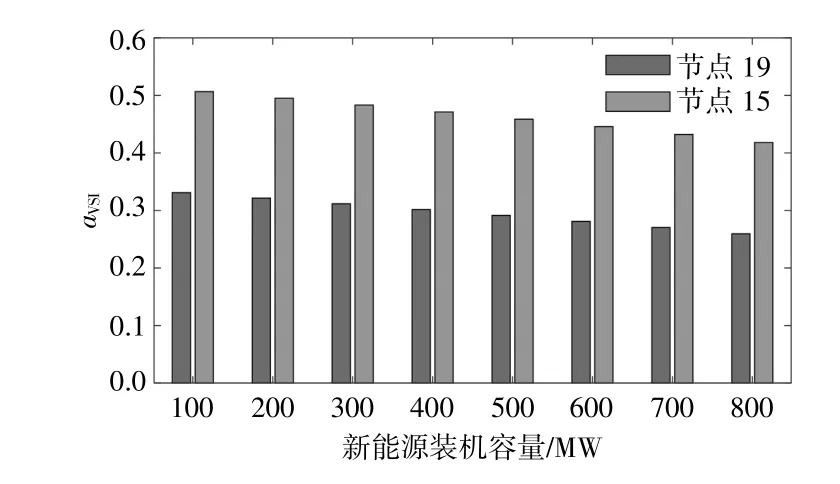
图6 新能源装机容量增长过程中不同节点的aVSI值Fig.6 aVSI values of different nodes in the process of new energy installed capacity growth

3.2 UPFC对系统静态电压稳定性的提升

UPFC作为目前先进的柔性交流输电装置之一，结构简洁、功能强大，适用于解决电网整体电压稳定问题。本文将UPFC安装在系统最薄弱节点位置，验证UPFC对提升新能源电网稳定性的有效性。由图5可知，在电压稳定指标下确定的系统最薄弱位置为节点19，此处最容易出现电压失稳现象。在IEEE-RTS79节点系统中最薄弱节点19处与较为薄弱的典型节点15处分别安装UPFC装置。表1为在不同薄弱节点位置安装UPFC对电压的提升，表2为新能源并入电网后薄弱节点电压的变化。

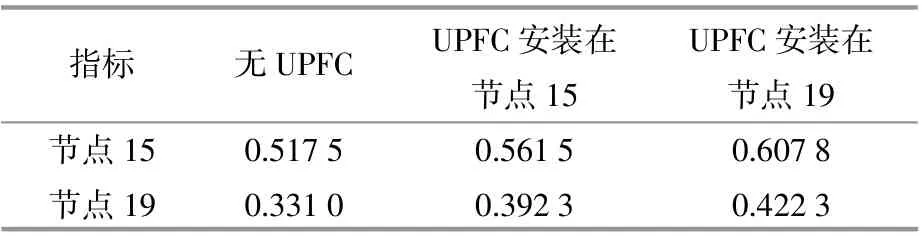
表1 不同位置下安装UPFC对薄弱节点电压的提升Table1 Voltage enhancement of weak nodes by installing UPFC at different locations p.u.

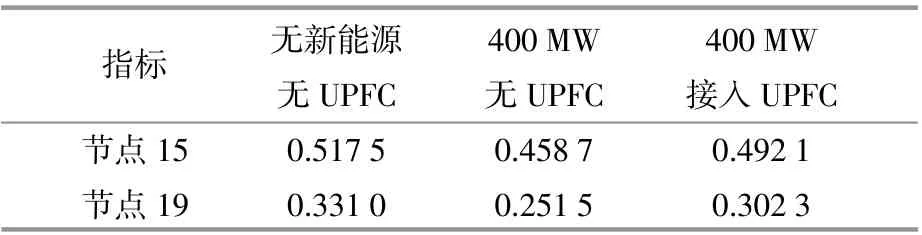
表2 新能源并入电网后薄弱节点电压的变化Table2 Change of weak node voltage after new energy is incorporated into power grid p.u.

通过表1与表2的结果对比可知，无论是否接入新能源，UPFC均能提升电网的静态电压稳定性。系统接入新能源后，节点19处的aVSI值下降了0.0795p.u.，节点15处的aVSI值下降了0.0588p.u.，这表明距离新能源负荷节点越近，电压下降速率越快。当系统在最薄弱节点19处安装UPFC后对整体电压稳定性的改善更加明显，aVSI值提升了0.0913p.u.，将500kV UPFC配置在节点19处后 ，线路16～19阻塞处潮流减小，且由线路16～19组成的送端断面功率逐渐减小，系统静态电压稳定指标值增加，系统静态电压稳定性增强。同时也表明UPFC对潮流的控制能力与接入薄弱节点位置的距离成正相关，距离薄弱节点越近，UPFC装置调节支路潮流的能力越强，同时可降低扩建输电设备的投资，增强新能源电网运行时的安全性与经济性。

4 结论

本文将UPFC应用于改善新能源电网下的静态电压稳定性，提出基于UPFC等效功率注入模型的潮流计算方程，并基于潮流计算方程提出反映系统静态电压稳定的效能评估指标。计算分析接入不同容量新能源对系统静态电压的影响以及UPFC对系统薄弱节点静态电压的提升，得到以下结论。

①新能源并入电网后系统静态电压稳定性降低，UPFC通过注入功率的方式调节薄弱节点电压，有效提升新能源电网的安全稳定性。

②对当前系统运行状态进行静态电压稳定分析，在系统薄弱节点安装UPFC能更好地提升整体安全稳定性。

③UPFC对潮流的控制能力与接入薄弱节点位置的距离成正相关，距离薄弱节点越近，UPFC装置调节支路潮流的能力越强，同时在薄弱节点处安装UPFC可有效降低扩建输电设备的投资，提升新能源电网运行时的安全性与经济性。