新能源运行容量可信度的精细化评估方法
王榆楗,吴 琼,柳 璐,张啸虎,桑 妲,刘盾盾,程浩忠
(1.上海交通大学 电气工程系,上海 200240;2.中国长江电力股份有限公司,北京 100038;3.国家电网有限公司华东分部,上海 200002;4.珠海澳大科技研究院,广东 珠海 519085;5.贵州电网有限责任公司电力调度控制中心,贵州 贵阳 550000)
0 引言
以风电和光伏为代表的可再生能源装机容量将持续快速增长,然而,风光可再生能源的间歇性与波动性导致其难以准确计入电力平衡[1]~[3]。当前电网以风电5%和光伏0%作为参与电力平衡的容量系数,无法满足未来以可再生能源为主体的新型电力系统发展需求。客观准确评估风光可再生能源可信度对于电力系统规划、运行具有十分重要的意义。
新能源机组能替代常规机组的容量即为置信容 量 或 可 信 容 量(Capacity Credit,CC)[4],约 有10余种指标用于定量评估[5],现有大量文献分别从不同角度分别对风电、光伏容量可信度的计算方法及影响因素进行研究。文献[6]研究风电穿透率水平、风资源优劣程度对容量可信度的影响。文献[7]基于人工神经网络提出经验模型,用于评估光伏容量可信度。文献[8]在光伏容量可信度评估过程中考虑了天气不确定性。文献[9]评估了储能对光伏容量可信度的影响。文献[10]在可靠性计算中考虑需求响应的影响,并应用于可信度评估。考虑相关性方面,基于历史数据的评估结果表明,风光新能源出力特性与系统负荷的相关性对于容量可信度评估结果具有显著影响[11]。文献[11]研究表明,风电出力与系统负荷之间的相关性越强,风电容量可信度就越大。文献[12]通过Spearman秩相关系数描述光伏出力与负荷相关性,并用于光伏容量可信度评估。文献[13]通过建立离散联合概率分布对光伏出力与负荷相关性进行建模并进行可信度评估;考虑“光-荷”相关性的评估结果均表明光伏出力和负荷之间的相关性对于光伏容量可信度具有积极影响。文献[14]通过单一Copula函数建立多风电场出力的联合概率分布,提出了考虑多风电场出力相关性的容量可信度评估方法。文献[15]在多光伏电站出力建模中考虑了空间相关性,并且分析了天气类型对于光伏出力的影响。文献[16]通过2维Archimedean Copula函数对风电、光伏出力相关性进行建模,并应用于可靠性评估。
现 有 研 究 分 别 从“风-光”、“风-荷”、“光-荷”角度进行考虑。然而,同一时刻、不同位置的风速、光照强度和负荷分布特性各异,并且相邻风电厂、光伏电站之间既不完全独立,也不完全相关,具有非线性相关性,同时“风-光-荷”三者之间亦具有非线性相关性[17]。因此在可信度评估中对风电出力之间、光伏出力之间以及风光荷之间的相关性进行准确建模,其难点在于单一类型Copula函数对“风-光”或者“风-荷”相关性能够较为准确的建模,但对于“风-光-荷”相关性建模,则准确性较低;此外采用参数分布也难以准确描述风光荷的分布特性。风光容量可信度评估均为长时间尺度(通常为1a),因此计算结果表征全年风、光新能源对该区域内电力系统充裕度的综合贡献[18],未能体现风、光新能源的时空分布特性。且仅有少量文献同时考虑了风电、光伏联合发电系统的综合容量可信度评估[19],[20]。因此,现有可信度评估存在计算方法对于风-光-荷多维时空相关性的考虑有所欠缺,使得计算结果不够精确、评价指标偏笼统、未计及系统运行备用,从而对于实际运行场景指导意义相对有限,有必要考虑更为精细化、具有实用性指导价值的扩展性指标与计算方法。
本文采用D-vine Pair Copula函数对多维风光荷相关性进行建模,并在系统运行可靠性不变的前提下,定义各时刻运行容量可信度指标,对特定运行场景进行精细化考虑,采用我国某实际区域电网2018-2020年风光荷历史数据,生成蕴含相关性的计算样本,计算风光运行可信容量,以期为系统实际运行中的电力平衡分析提供参考。
1 风光荷相关性数据建模及采样
1.1 Pair Copula风光荷相关性建模
对 于 多 元 随 机 变 量x=(x1,x2,…,xd),xk的 边缘累积分布函数为Fk(xk),Sklar定理给出了多维联合分布H(x)与Copula函数C(u)之间的关系:
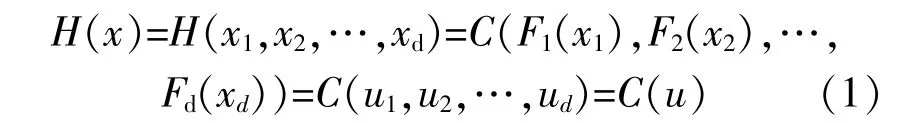
式 中:uk=Fk(xk),且uk服 从[0,1]均 匀 分 布。
对式(1)求导,得到多维联合概率密度函数:
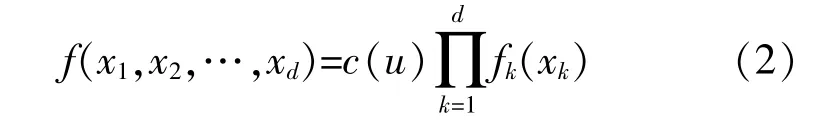
式 中:c(u)为Copula密 度 函 数;fk(xk)为xk的 边 缘概率密度函数。
由式(2)可见,通过估计随机变量的边缘密度函 数fk(xk)(k=1,2…,d),并 通 过 估 计d维Copula密度函数c(u)表示相关性结构,可求得联合概率密 度 分 布f(x1,x2,…,xd)。现 有Copula函 数 能 够 对二维相关性建模较准确,但对于多维变量的相关性 建 模 则 不 够 准 确[21],[22],而Pair Copula理 论[23]将多维Copula函数的密度函数c(u)拆分为一组2维Copula密度函数和随机变量边缘概率密度函数的乘积,从而能较好描地述复杂的多维相关性。
本文采用D-vine Pair Copula结构作为c(u)的分解方式,d维D-vine结构如图1所示。

图1 d维D-vine Pair Copula结构图Fig.1 Structure diagram of d-dimensional D-vine Pair Copula
d维D-vine Pair Copula结构有d-1层,第Li层有d-i个节点。
结 构 中c(u)表 达 式 为
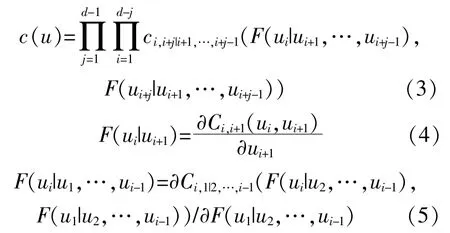
通过Pair Copula将随机变量两两合并,并采用相应的二元Copula函数描述,从而可以提高模型拟合精度,更加准确地描述多维“风-光-荷”之间不同的相关性结构。
本文采用欧氏距离法[22],作为评价Copula模型对于原始样本数据拟合效果的评价方法。
记(x1i,x2i,…,xdi)为d维 随 机 变 量x的 历 史 数据 样 本,其 中i=1,2,…,N,N为 历 史 数 据 样 本 总数。拟合得到的欧氏距离为
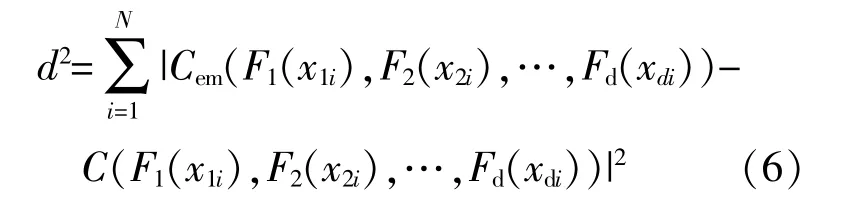
式中:Cem(·)为从历史数据中获得的在样本点处的实际概率值。
采用非参数核密度估计法(Kernel Density Estimation,KDE)分别估计多维风光荷数据的概率 密 度 函 数fk(xk)、累 积 分 布 函 数Fk(xk)及 其 反 函数Fk-1(xk),再 利 用 累 积 分 布 函 数Fk(·)将 数 据xk变换为均匀分布的概率。
随机变量xk的核密度为
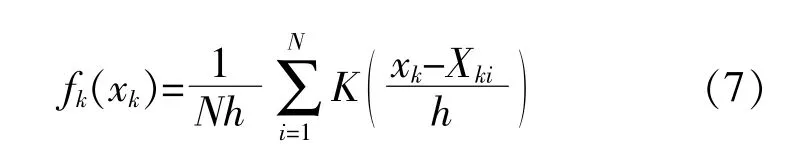
式 中:h为 带 宽;K(·)为 核 函 数;Xki为 随 机 变 量xk的第i个历史样本。
当样本数据给定,fk(xk)便可由核函数以及带宽确定。KDE中通常采用高斯核函数为
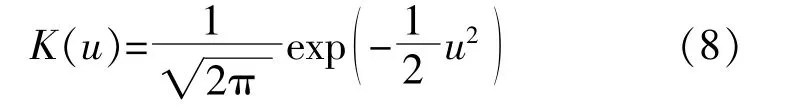
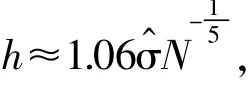
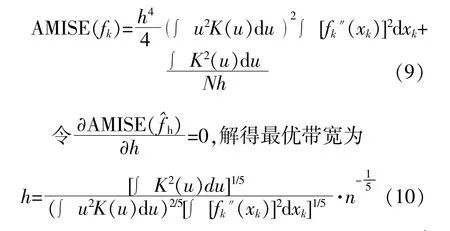
对式(7)积分可得随机变量xk的边缘累积分布函数为
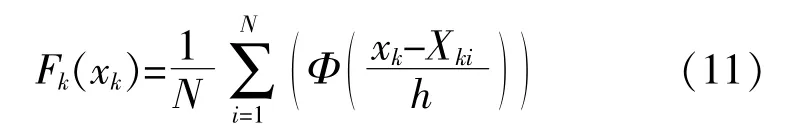
1.2 建模及采样流程
基于D-vine Pair Copula结构以及非参数核密度估计方法,对d维风光荷相关性进行建模并采样生成数据。步骤如下。
①读 入d维 风 光 荷 历 史 数 据(X1i,X2i,…,Xdi)i=1,2,…,N,利用KDE得到各随机变量相应的边缘 概 率 密 度 函 数fk(xk)和 累 积 分 布 函 数Fk(xk)。
②令uk=Fk(xk),将 历 史 数 据 相 应 带 入,得 到均 匀 分 布U=[U1,U2,…,Ud]的 样 本 点。
③根据样本数据U,对第L1层各Copula密度函数进行拟合,采用对数极大似然估计得到相应参数。依据式(6)对拟合度进行检验,选出第L1层各最优2维Copula密度函数。
④将式(4)所示的条件分布作为新的随机变量,并利用U的样本和式(4)得到其样本。采用式(4)中条件分布得到的样本,依据式(6)对拟合度进行检验,选出第L2层各最优Copula密度函数。
⑤通过前一层条件分布的样本以及式(5)生成本层条件分布的样本,与上述步骤类似,直至得到第Ld-1层的Copula密度函数,并得出式(3)。
⑥按数据进行采样,生成蕴含d维风-光-荷相 关 性 的 数 据(X1,X2,…,Xd),采 样 函 数 为
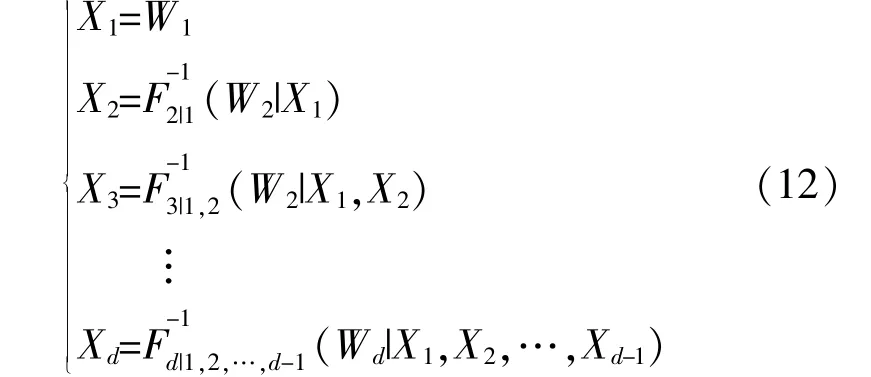
式 中:W1,W2,…,Wd为 通 过 蒙 特 卡 洛 生 成 在[0,1]上服从均匀分布的随机数;F-1为式(3)中各累积分布函数的逆函数。
2 风光运行容量可信度评估方法
2.1 风-光运行容量可信度指标
现有容量可信度评估指标以等效可靠容量(Equivalent Firm Capacity,EFC)为 代 表,EFC为 实际系统除去风光机组并加入特定容量,且100%可靠的虚拟常规机组后,系统可靠性与实际系统可靠性相同,此时虚拟常规机组容量占风光新能源装机容量的比例为风光容量可信度[18]。
在实际运行中,为保证系统各时刻运行可靠性,需配置一定的备用容量,在风光新能源装机较多的地区,还需结合风光出力特性和参与电力平衡的比例,额外设置一定的负荷备用容量[24]。按照EFC定义,对于运行中风光容量可信度评估存在适应性问题。即目前运行中是以一定负荷比例设置备用,从而确定开机容量,此时存在原系统中的风光应该以多少容量计入系统开机容量的问题,开机容量改变,系统可靠性相应改变,从而直接影响到最终的计算结果。
本文在系统运行可靠性不变的前提下,考虑系统运行备用,定义风光新能源各时刻的运行可信 容 量(Operational Credit Capacity,OCC),其 表达式为
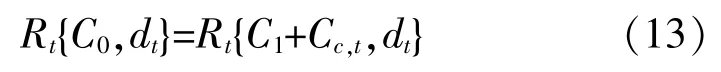
式中:Rt为系统t时刻的可靠性,选取失负荷概率(Loss of Load Probability,LOLP)作 为 可 靠 性 的 判断标准,等式左侧为不含风光系统;C0为根据负荷设置备用容量后,系统常规机组开机容量;dt为t时刻系统负荷,等式右侧为风光接入后系统;C1为风光接入后系统常规机组开机容量;Cc-t为风光新能源在t时刻的运行可信容量,Cc-t与风光新能源装机的比值,即为风光新能源t时刻的运行容量可信度。
在OCC定义下,首先根据负荷设置备用,确定系统常规机组开机容量,并评估该时刻的系统可靠性;之后将风光新能源加入系统,在等可靠性前提下,常规机组开机容量将相应减少,此时,常规机组开机容量的减少量 ΔC=C0-C1即为t时刻风光新能源运行可信容量Cc-t。
2.2 考虑风-光-荷相关性的发电系统可靠性计算方法
通过前文方法生成蕴含多维风-光-荷相关性的计算样本后,采用基于重要抽样法的蒙特卡洛法对发电系统可靠性进行计算。常规机组可靠性模型为
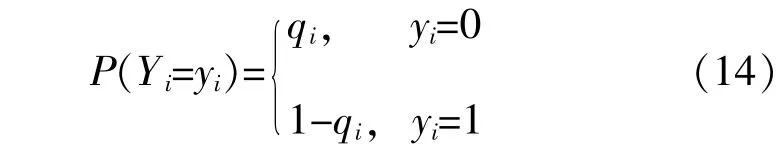
式中:P(g)为系统状态分布;Yi为系统状态向量第i个元素;yi为常规机组i的状态;qi为常规机组i的强迫停运率。
对于受端系统可靠性评估,本文将直流输电系统的注入功率等效为多状态电源,等效方式参见文献[25]。此外,还需根据历史运行方式考虑直流线路不同月份的输送容量。例如对于水电送端直流,汛期(6-9月)输送容量按额定容量计,其余月份则按60%额定容量作为双极完全运行时的输送容量。
运行容量可信度评估过程中,涉及多次迭代计算系统可靠性,蒙特卡洛法需花费大量计算时间。为减小计算耗时,本文引入重要抽样法,在维持样本期望值恒定的前提下,改变现有样本空间的概率分布,缩小计算指标的方差,以提高运算速率[26]。以 系 统 状 态 函 数S(Y)的 期 望E(S)作 为 可靠性评估指标,采用方差系数作为收敛判据[26],其表达式为
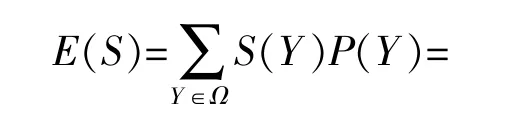
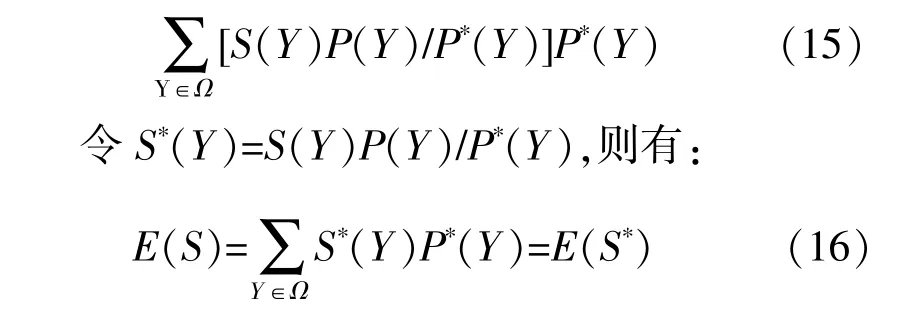
式中:Ω为状态空间;S*(Y)为新状态分布下的系统状态函数。
若新状态分布P*(Y)能够突出“重要事件”(即引起系统故障停运的事件),则能够证明S*(Y)方 差 将 小 于S(Y)方 差。新 分 布P*(Y)又 称为重要分布函数。定义系统重要分布函数为
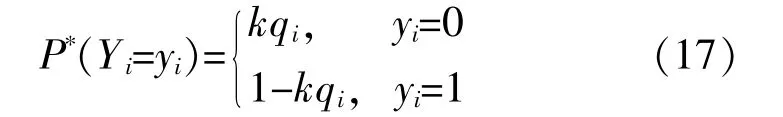
式中:k为重要乘子。
2.3 风光运行容量可信度评估流程
根据OCC定义,考虑相关性的风光新能源运行容量可信度评估流程,如图2所示。
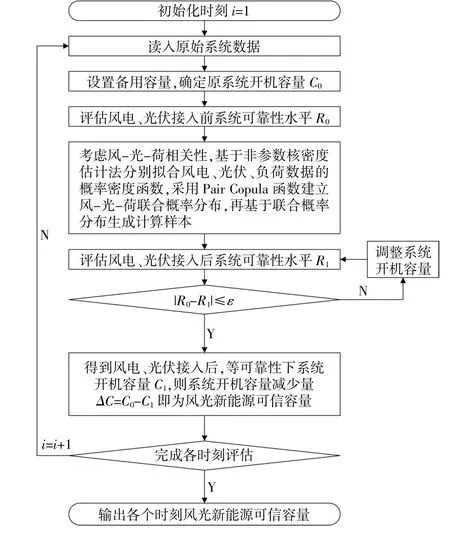
图2 考虑相关性的风光新能源运行容量可信度评估流程Fig.2 OCC evaluation flow chart of new energy considering relevance
首先读入原始系统数据:常规机组装机容量、强迫停运率数据、直流受电功率、历史数据集内每日i时刻的风电、光伏及负荷数据。根据负荷情况确定原始系统中常规机组开机容量C0,评估原始系统可靠性R0。开机容量为峰值负荷加上备用容量,系统备用需求源于电网运行中的不确定性,一方面是不可预计的电网事故(事故备用),另一方面是供需预测的不准确(负荷备用),通常为峰值负荷的2%~5%。然后,生成蕴含多维风-光-荷相关性的计算样本,计算风光新能源接入后系统可靠性R1,通过弦截法[18]调节常规机组开机容量C1使风光新能源接入前后系统可靠性指标相差在一定误差范围内,此时,常规机组开机容量的减少量ΔC=C0-C1,即为t时刻风光新能源运行可信容量。
3 算例分析
我国某实际区域电网总装机38317万kW,电源结构如图3所示。各子区域相对位置如图4所示。馈入区域电网的跨区直流总额定容量为6976万kW,网内最大负荷为31871万kW;采用2018-2020年迎峰度夏期间(6-8月)15min间隔的风光荷历史数据拟合边缘分布,其中风电、光伏出力数据为出力占装机的百分比,由5个子区域分别采集,各子区域风光装机占比如表1所示,负荷则按最大功率标幺化。
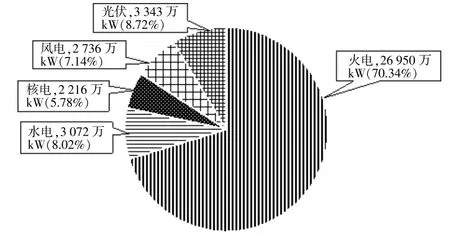
图3 区域电网电源结构Fig.3 Power source structure of regional power grid
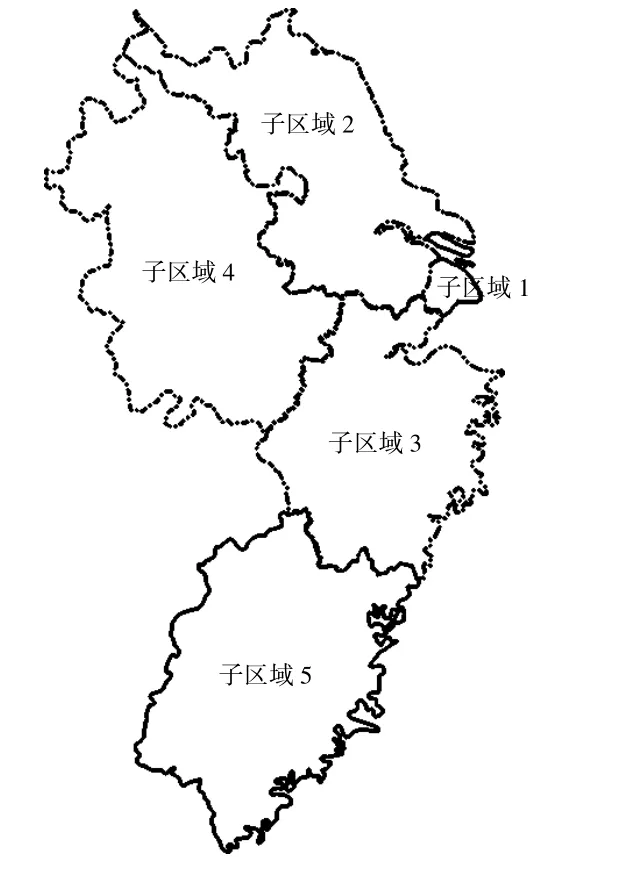
图4 各子区域相对位置Fig.4 The relative position of each sub-region
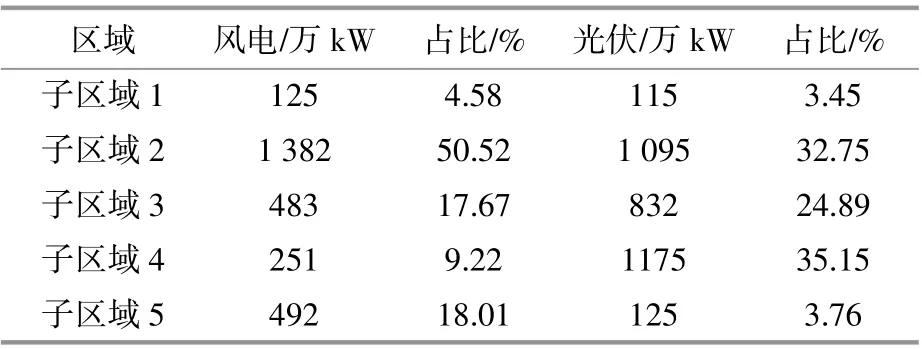
表1 子区域风光新能源装机结构Table1 Sub-regional new energy installed structure
3.1 风-光-荷相关性模型验证
对历史数据集内每日12:00-13:00的风电、光伏及负荷数据,采用KDE拟合边缘概率密度以及累积概率,拟合结果如图5所示。
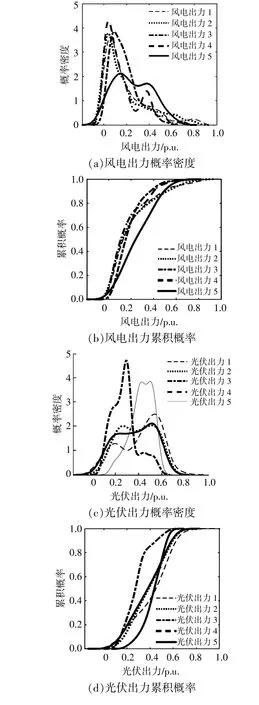
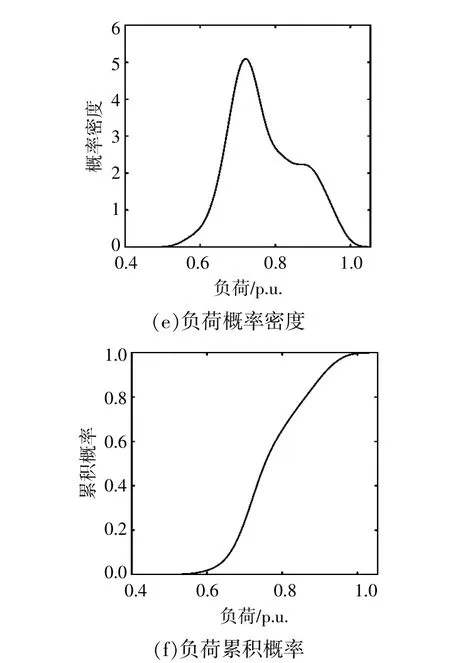
图5 历史数据集内12:00-13:00风电、光伏出力和负荷的概率密度和累积概率Fig.5 Probability density and cumulative probability of wind power,photovoltaic power and load
由图5可以看出,仅采用Weibull分布无法准确描述各风电出力的概率密度和累积概率。同样,各光伏出力也难以用Beta分布进行描述。而负荷的概率密度曲线在形态上也与正态分布明显不同。与风-光-荷服从特定参数分布相比,采用KDE有利于提高Pair Copula模型准确度。采用Wi,Pi(i=1,…,5)及L分 别 代 表 各 风 电、光 伏 及 负荷功率,对多维风光荷之间分别进行2维最优Copula建模,最优Copula函数如表2所示。分别考察高维normal Copula、高维t Copula,以及Dvine Pair Copula对于多维风光荷拟合效果,欧氏距离如表3所示。

表3 不同Copula函数对于高维风光荷建模的欧式距离Table3 The Euclidean distance of different Copula functions for modeling high-dimensional wind power,photovoltaic and load
由表2,3可以看出,大量2维变量的最优Copula并非normal Copula或t Copula,相较于高维normal Copula与 高 维t Coupula,D-vine Pair Copula由于引入多种Copula函数,能够更好的对多维风光荷间复杂的整体与局部相关性进行建模,从而为风光运行容量可信度计算的准确性提供保障。

表2 各2维最优Copula函数类型Table2 Optimal Copula function types of2dimension
3.2 迎峰度夏期间峰值负荷日风-光运行可信容量评估
以迎峰度夏期间出现峰值负荷(31871万kW)时的日负荷情况为例,确定系统开机容量,并评估系统运行可靠性,在系统运行可靠性不变的前提下,基于本文所述方法进行该日各时刻(24 h)风、光运行可信容量评估,结果如图6所示。由于夏季光伏仅在6:00-19:00出力,因此其余时刻仅考虑多维风-荷相关性。
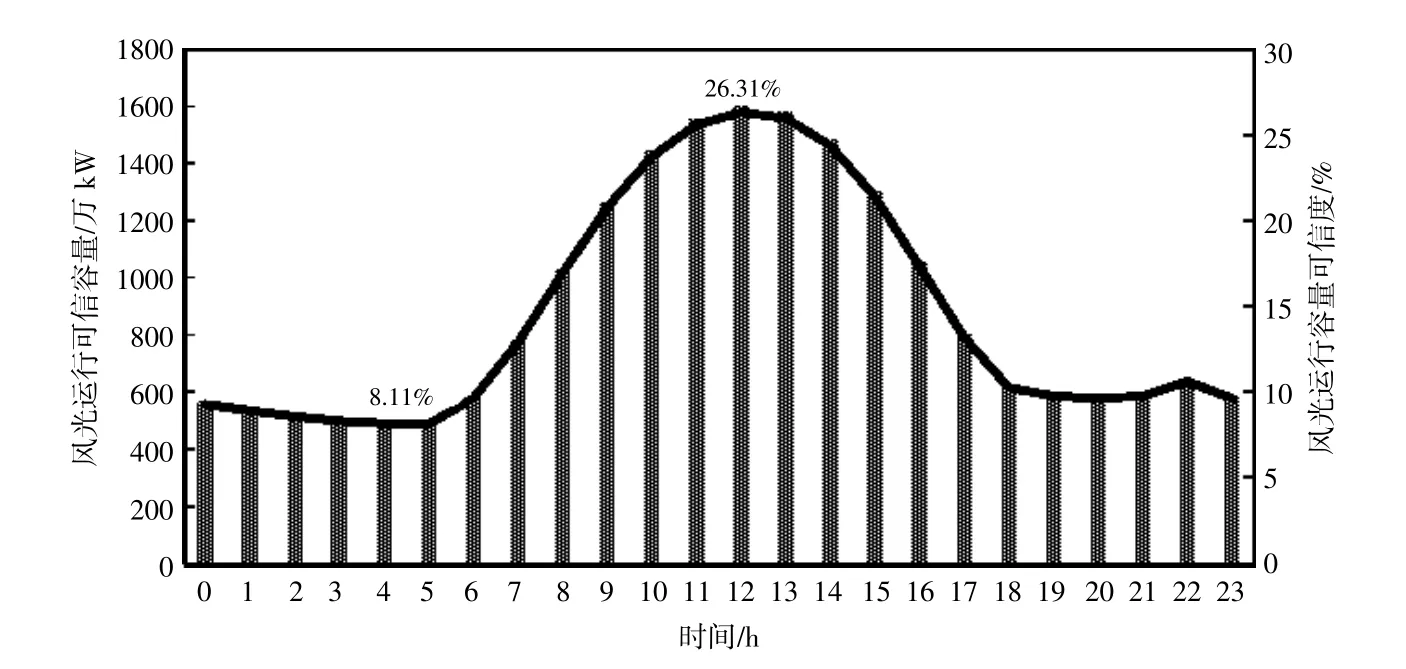
图6 迎峰度夏期间峰值负荷日风光运行可信容量计算结果Fig.6 Calculation results of OCC of peak load during summer
根据计算结果,日间风光运行容量可信度均大于10%,最高达到26.31%;夜间仅考虑风电,运行容量可信度最低为8.11%,其余时刻接近10%。由于风光新能源的间歇性、波动性和随机性,目前我国调度系统往往在日前计划中对风光出力考虑的比较保守,因此在未来安排系统日前发电计划时,可根据负荷预测结果按本文所述方法计算风光运行可信容量,并结合风电、光伏出力预测,从而更加合理的安排常规机组的发电计划。
EFC定义下,仅采用6-8月风光荷历史数据进行评估,容量可信度为19.43%,评估结果表征风光新能源对系统电力充裕度的综合贡献,忽略了风光新能源时空分布特性,对于实际运行中的电力平衡指导意义相对有限。针对不同季节的风光新能源时空分布特性,同样可采用本文所提指标与方法进行相应计算。相较于仅以一个定值表示风光可信容量的传统计算方法,本文对可信度评估指标体系及评估方法进行了拓展,且更加精细化的考虑了多维风光荷时空分布特性,以期为风光新能源参与电力平衡提供参考。
3.3 风、光装机容量对运行可信容量的影响
“双碳”背景下,风电、光伏装机容量将进一步快速增加。为探究风光装机容量对于运行可信容量的影响,本节在保持现有负荷不变的情况下依据现有各子区域风光装机容量的占比关系对风光总装机容量进行线性外推,计算午间12点不同风光总装机容量下的风光运行可信容量,结果如图7所示。
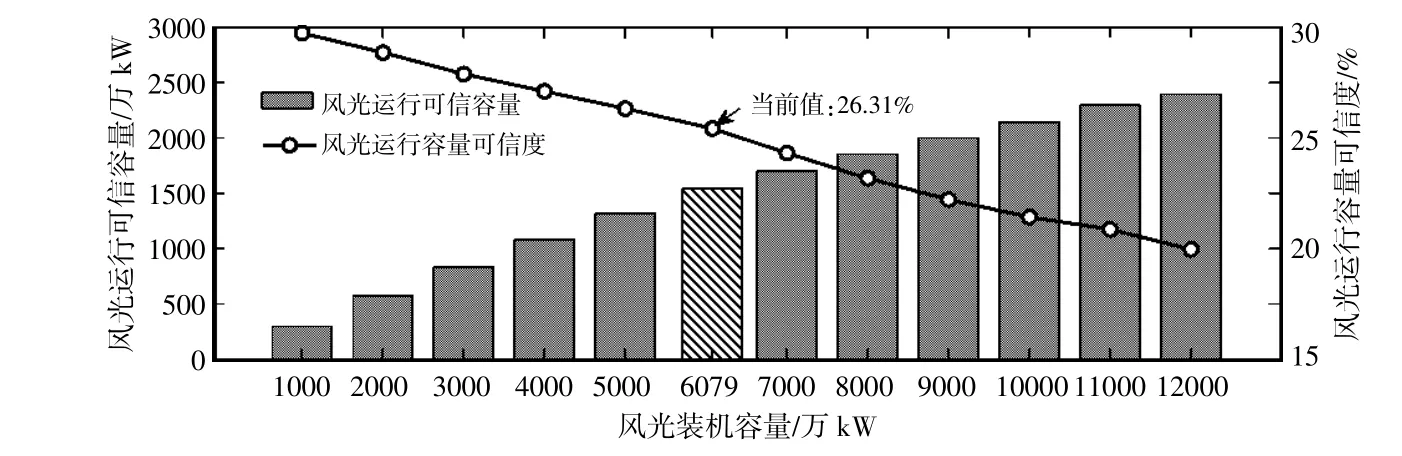
图7 不同风光装机容量下运行可信度评估结果Fig.7 OCC results under different installed capacity
由图7可以看出,随着风光装机容量增加,可信度从1000万kW装机时的29.74%逐渐下降至12000万kW装机时的19.97%。以1000万kW为梯度,增加同样风光装机的边际效益下降,即风光运行可信容量增长幅度降低,存在饱和效应。这是由于风光装机容量较少时,系统可靠性主要取决于常规机组状态,而风光装机容量增加后,根据指标定义,常规机组开机容量减少,因此风光出力的波动性对于系统可靠性的影响会进一步增大,为维持系统等可靠性,常规机组开机容量的减少幅度也会相应减小。
4 结论
本文针对可信度指标尚未深入应用于运行阶段的问题,定义了运行容量可信度指标,提出考虑多维风光荷相关性的运行容量可信度评估方法,该方法引入D-vine Pair Copula,采用历年风-光-荷数据对多维风光荷相关性进行建模,利用基于重要抽样法的蒙特卡洛法对系统可靠性进行评估,并采用弦截法迭代,实现对给定运行场景的风光运行可信容量评估。本文通过算例分析得到结论如下:①多维风光荷具有复杂非线性相关性,Pair Copula函数对于各随机变量之间的相关性均采用最优2维Copula函数建模,使得生成的风光荷数据包含更多的相关性特征,此外采用KDE能够有效提高建模准确性。因此相较于传统容量可信度计算中对于风-光-荷的考虑方法,本文采用方法考虑因素更加全面,能获得更准确的计算结果;②本文所提指标与方法更精细化考虑了多维风光荷相关性,以某实际区域电网迎峰度夏期间峰值负荷日的负荷情况为例,计算各时刻(24 h)风光运行容量可信度,结果为8.11%~26.31%。运行中仅以风电5%和光伏0%作为参与电力平衡的容量系数会导致过多的开机,进而影响风光消纳。安排系统日前发电计划时,可根据计算结果并结合风光出力预测,为调度安排合理开机计划提供参考。探究了风光装机容量对于运行可信容量的影响,计算结果表明,随着风光装机容量增加,可信容量存在饱和效应。
储能可以弥补新能源在随机波动性方面的先天缺陷,随着储能系统的大规模引入,风-光-储联合系统有望得到广泛应用,在后续研究中可考虑采用序贯蒙特卡洛模拟法进行风-光-储联合系统的可靠性评估,以及考虑风光荷时间相关性的建模与采样,进而精细化评估风-光-储联合系统的运行容量可信度。

