基于改进下垂控制的双馈风电机组频率控制策略

许益恩，张新松，李大祥，张罗玉，陈 沛，杨德健

（1.南通大学 电气工程学院，江苏 南通 226019；2.东北电力大学 电气工程学院，吉林 吉林 132012）

0 引言

近年来，在能源电力转型的时代背景下，以风电为代表的新能源发电在电力系统中占比不断增加[1]。截至2021年11月底，我国风电累计装机容量达300GW，约占全国电源装机总量的13%，位 居 世 界 第 一[2]。

变速恒频双馈风力发电机（Doubly-Fed Induction Generator，DFIG）具 有 体 积 较 小、控 制 灵活等特点，已成为当前风电场的主流机型之一。该风力发电机通过变流器并网，风机转速与系统频率解耦。当系统发生扰动后，DFIG无法提供频率响应服务[3]，[4]。另外，随着风电渗透率的不断提高，越来越多的火电机组被取代，电力系统整体惯性水平降低[5]。当系统发生较大的频率扰动事件时，频率跌落严重，容易触发第三级别系统保护动作，给系统频率稳定性带来巨大的挑战[6]。因此，一些高风电渗透率的国家明确要求风电机组像常规机组一样，具备一定的调频能力[7]，[8]。

目前，DFIG利用自身灵活的控制能力参与系统频率调控大致分为功率备用控制策略和转子动能控制策略[9]。其中，功率备用控制策略包含变桨控制和转子超速控制。然而，风机长期运行于减载模式，不利于风电场经济运行[10]，[11]。相比之下，转子动能控制策略利用风机叶片存储的能量参与频率调节，在保证风电场经济效益的同时，还 取 得 了 良 好 的 调 频 效 果[12]，[13]。

文献[14]通过附加辅助控制环节，使DFIG模拟出一次频率响应。然而，采用固定增益策略在一定程度上限制了风电机组的调频潜力。文献[15]研究了不同控制增益下的风机下垂控制性能。为提高风机调频能力，文献[16]，[17]提出了基于风机转子转速的下垂控制增益，却忽略了扰动后系统频率动态特性。文献[18]基于风电机组比例微分（PD）虚拟惯性控制的基本原理，推导了PD虚拟惯量控制与系统频率的量化关系。通过分析可知，比例系数主要影响系统频率最低点，对频率跌落速度影响较小。上述文献对于风机下垂增益的设定均未考虑系统频率实际变化状态，无法根据系统实时频率特性动态调整。若扰动发生后频率变化较快，系统有功缺额大，则风机无法及时为系统提供频率支撑，无法有效改善电力系统频率动态性能。

为弥补现有调频方法的不足，本文提出一种基于改进下垂控制的双馈风电机组调频策略。该策略从系统角度出发，对传统下垂控制策略中的控制增益加以改进，引入关于系统频率变化率的增益分量，使风机根据系统状态实时调节调频补偿功率，从而改善系统频率响应特性。通过基于EMTP-RV搭建的含DFIG的四机系统模型进行仿真研究，验证了所提改进策略的有效性。

1 双馈风力发电机组建模

双馈风力发电机主要包括风力机、传动轴、感应发电机、背靠背式变流器及其控制系统，其基本结构如图1所示。DFIG控制系统主要由桨距角控制、转子侧变流器、网侧变流器组成。桨距角控制用于防止风机转子转速过高。转子侧变流器通过将定子电压保持在理想的参考电压，调整注入电网的有功功率，实现风机最大功率跟踪（MPPT）运行。网侧变流器用于维持直流环节电压的稳定。

根据空气动力学原理，风力机捕获的输入机械功率Pm为

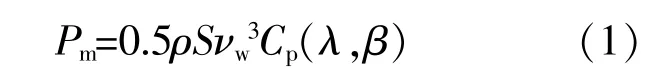
式中：ρ为空气密度；S为风机叶片迎风扫掠的面积；νw为风速；λ为风机叶尖速比；β为桨距角；Cp为风能利用系数，其计算式如式（2）所示[19]。

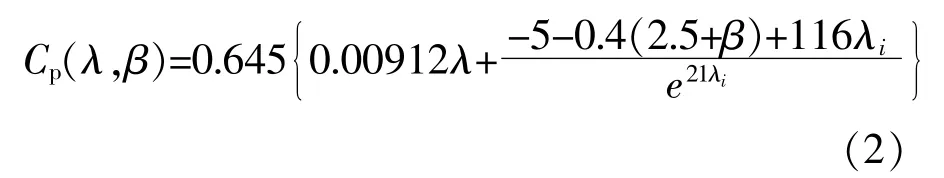
由 式（2）可 以 得 到 不 同 β值 的Cp（λ）与 λ关系 曲 线（图2）。

当 λ=λopt，β=0°时，风 机 可 获 得 最 大 风 能 利用系数Cp，max，对应此时DFIG工作在MPPT运行模式，其输出功率PMPPT可表示为

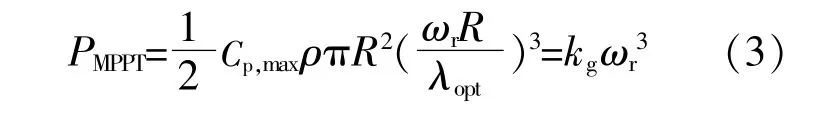
式中：R为风机叶轮半径；λopt为风机捕获最大风能的最佳叶尖速比，λopt取值为9.95；kg是关于风机特征参数的一个计算常量，可由式（4）求得。

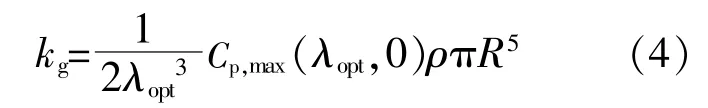
2 系统频率稳定性分析

受扰动影响，电力系统中总有功出力与负荷消耗功率产生不平衡，电网频率发生偏移。在仅考虑同步发电机组参与系统调频的情况下，系统频率的动态响应方程可表示为

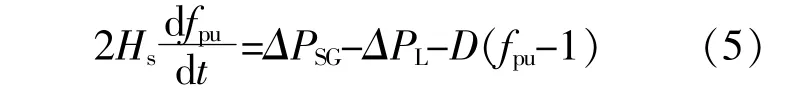
式中：Hs为系统惯性常数；fpu为系统频率标幺值；ΔPL为扰动功率；ΔPSG为同步机组参与调频的有功变化量；D为负荷阻尼系数。

在系统发生扰动的初始时刻，有 ΔPSG|t=0+=0，（fpu-1）|t=0+=0，可得系统频率变化率最大值为

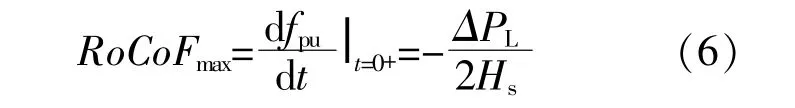
由文献[20]可知，受扰后系统频率偏差可由单机系统频率响应（SFR）模型推导而得，如式（7）所示。

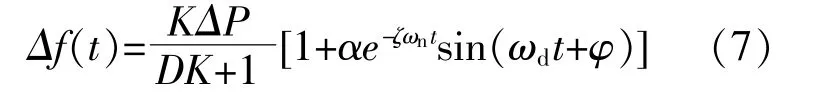
式中：ΔP为等效扰动功率；K为同步机组调速器的调速增益；ζ为阻尼比；ωn为自然振荡频率；ωd为阻尼角频率；α和 φ为单机SFR模型推导过程产生的系数。

对 式（7）进 行 求 导，得：

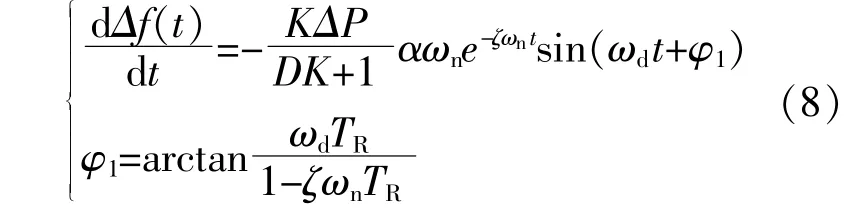
式中：TR为机组再热时间常数。

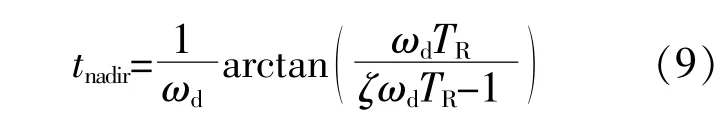
将 式（9）带 入 式（7），可 得 系 统 最 大 频 率 偏 差表达式：

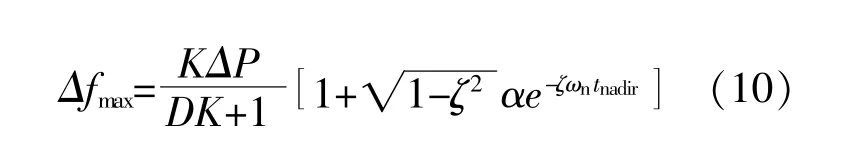
从 式（6），（10）可 以 看 出，受 扰 后 系 统 频 率 变化率最大值RoCoFmax、系统最大频率偏差 Δfmax与负荷扰动呈正相关，扰动越大，系统频率跌落速度越快，最大频率偏差越大。另外，随着以风电为代表的新能源大规模联网，系统整体惯性Hs和调速增益K削弱，恶化了系统频率稳定。因此，考虑风电机组参与系统调频有助于提高系统惯性水平，从而改善系统动态频率稳定性。

3 双馈风电机组改进下垂控制

3.1 传统下垂控制

传统下垂控制通过在双馈风机转子侧控制器中附加基于系统频率偏差（Δf）的控制回路来模拟常规同步发电机组的一次调频特性（图3）。

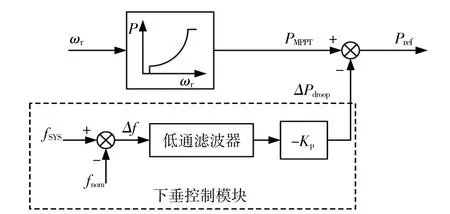
图3 下垂控制框图Fig.3 Control diagram of droop control

由图3可知，当系统频率因扰动越限时，DFIG启动虚拟惯量控制，其输出参考功率表示为

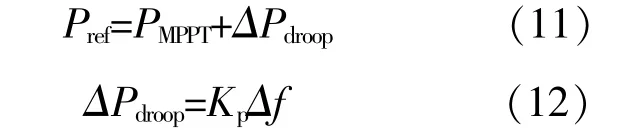
式中：PMPPT为最大功率追踪输出功率；ΔPdroop为附加下垂控制的有功增量；Kp为下垂控制系数。

扰动发生后附加下垂控制回路，使得DFIG能够响应系统频率变化而释放转子动能来增加有功输出，从而减少电力系统中的有功不平衡量，实现频率支撑。本文主要考虑低频扰动。

由式（12）可知，DFIG调频性能主要取决于下垂控制系数Kp的取值。传统下垂控制采用恒定控制增益，DFIG在参与调频时存在以下两种情形：①Kp取值过小，限制了DFIG调频潜力，风机转子动能得不到充分利用；②Kp取值过大，容易造成DFIG过度响应，导致风机失速[15]。

传统DFIG下垂控制主要影响系统频率最低点，对频率跌落速度（频率变化率）的影响很小[18]。因为在扰动初期，电网频率偏差 Δf较小，DFIG所提供的功率支撑（ΔPdroop）有限，对系统最大频率变化率的改善不明显；随着 Δf逐渐增大，ΔPdroop随之增加。由此可见，下垂控制有助于改善最大频率偏差。

综上所述，Kp的取值决定了DFIG的调频性能。通过定义合理的Kp，可以充分挖掘DFIG调频潜力，减少系统最大频率变化率，提高系统频率最低点，从而改善系统的频率响应特性。

3.2 基于RoCoF的DFIG改进下垂控制

为了弥补现有方法的不足，本文在传统下垂控制基础上考虑电网频率动态特性，提出基于频率变化率（RoCoF）的改进下垂控制策略（图4）。

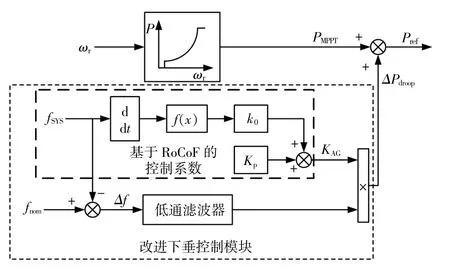
图4 基于RoCoF的改进下垂控制策略Fig.4 Improved droop control strategy based on RoCoF

如图4所示，改进下垂控制附加功率表达式为

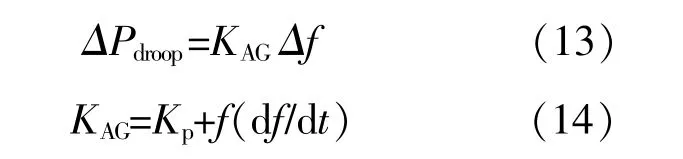
式 中：KAG为 改 进 的 控 制 增 益；f（df/dt）为 关 于 频 率变化率df/dt的增益函数。

基于EMTP-RV仿真平台，分析风机控制增益KAG在不同函数场景下的系统频率和双馈风机有功功率的变化曲线。仿真结果如图5所示。由图5（a）可知，当KAG分别定义为关于频率变化率df/dt的一次函数、指数函数、幂函数和对数函数时，对应的系统频率最低值分别为49.595，49.595，49.591，49.593Hz；最 大RoCoF分别 为-0.428，-0.437，-0.425，-0.438Hz/s。不 难 发现，当KAG定义为df/dt的不同函数形式时，风机参与调频对于缓解系统频率最低点和最大RoCoF的性能相似。但考虑到控制模型的搭建以及实际工程应用，一次（线性）函数更加便于实施。于是，在本文所提出的改进下垂策略中，选择将公式（14）中的函数形式设置为关于df/dt的线性函数。

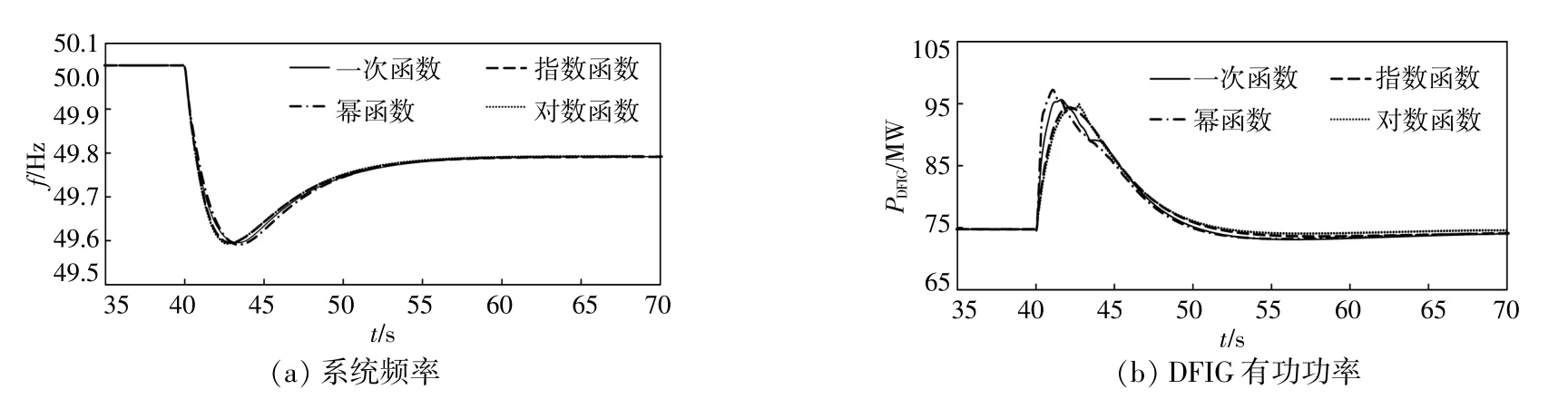
图5 KAG定义为不同函数时对DFIG调频性能的效果影响Fig.5 Influence of KAG with different functions on DFIG frequency regulation

综上所述，式（14）可进一步表示为

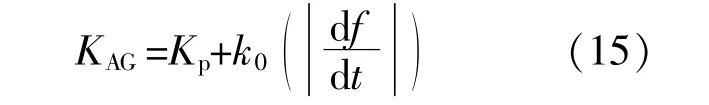
式中的KAG实质是关于系统频率变化率的线性函数。由于系统频率变化率可直观反映出系统扰动大小，因此改进下垂控制可在不同扰动场景下调整控制增益，实现DFIG输出功率的自适应调节，提高改进下垂调频策略对扰动的适应性。

式（15）中的k0为调频系数，用于调节风电机组频率支撑效果，其取值与系统遭受扰动大小和风机有效旋转动能有关。k0取值越大，控制增益KAG在扰动初始时刻变化越大，越有利于提高DFIG的频率支撑效果，从而改善最大df/dt和频率最低点。然而，k0取值过大，可能会导致频率响应初期KAG变化过快，进而引发更严重的频率事故；反之，k0取值过小，DFIG调频潜力受限。在实际工程应用中，可根据电力系统运行工况、惯性大小、功率扰动大小、风机有效旋转动能和控制目的，综合确定参数k0的取值。本文中，考虑风机有效旋转动能和扰动大小，将k0的取值暂定为50。在后续的研究中，将针对不同系统运行工况下k0的最优化展开进一步研究。

在系统发生扰动初期，系统中有功功率不平衡量最大。由转子运动方程可知，此时系统频率跌落速度最大[21]。借助式（15），与传统下垂控制相比，改进后的下垂控制策略获得了更优的控制增益KAG，从而控制DFIG在频率跌落初期向电网输出更多的有功功率，有效减少最大频率变化率和最大频率偏差。图6给出了设调频系数k0为50，固有下垂增益Kp为20时，改进下垂控制增益与传统下垂控制增益的对比。显然，由于附加了关于系统频率变化率的耦合项，在频率跌落期间，改进策略的控制增益始终高于传统策略。由此表明，采用了改进下垂控制，DFIG可以提供更好的频率支撑。

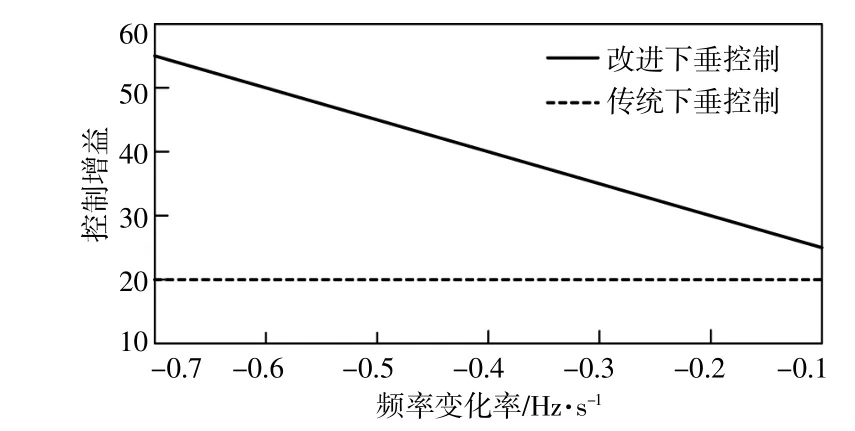
图6 改进下垂控制增益与传统下垂控制增益的对比Fig.6 Comparison between improved droop control gain and conventional control gain

4 算例分析

本文采用EMTP-RV搭建如图7所示的四机系统模型，对改进后的风机下垂控制策略进行仿真验证。该系统包含4台同步发电机SG1～SG4，1个聚合风电场及恒功率负荷。同步机SG1和SG2的额定容量为100MVA，SG3和SG4的额定容量为150MVA，所有同步机均采用IEEEG1调速器[19]。风电场包含34台5MW的双馈风力发电机。用电负荷包含1台异步电动机及容量为240 MVA静负荷。另外，设定在仿真40s时，同步发电机SG4脱机作为主要扰动事件。

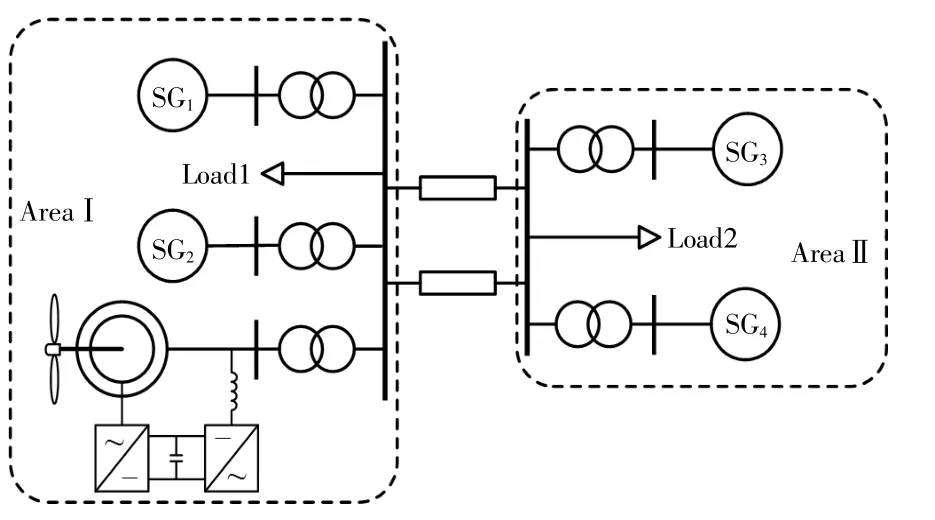
图7 仿真系统模型Fig.7 Model of simulation system

为讨论不同扰动工况对DFIG调频性能的影响，本文设置了以下两种算例场景：①扰动为70MW；②扰动为130MW。两种场景中风电渗透水平为20%，风速均为9.5m/s。在此基础上，对比DFIG在最大功率跟踪（DFIG不参与调频）、传统下垂控制和改进下垂控制的调频效果。

4.1 场景1

图8给出了场景1下电网频率、DFIG有功功率和转子转速的变化曲线。

图8 场景1的仿真结果Fig.8 Simulation results for Case1

由图8（a）可知，当DFIG采用最大功率跟踪控制、传统下垂控制和改进的下垂控制策略时，系统最大频率偏差分别为0.529，0.415，0.404Hz。与传统下垂控制相比，采用改进下垂控制时的系统最大频率偏差减少了2.65%，进一步提高了频率最低点。

由图8（c）可知，采用改进下垂控制策略时，DFIG有功功率由74.7MW增至95.6MW，功率增量为20.9MW；传统控制策略中DFIG有功功率由74.7MW增至92.9MW，功率增量为18.2MW。与传统下垂控制相比，采用改进下垂控制时，DFIG在频率响应期间提供了更多的功率支撑。这主要是由于改进下垂控制系数包含了关于系统频率变化率df/dt的耦合项，根据式（15）获得更大的下垂控制系数。图8（b）显示，采用改进下垂控制，可进一步减少最大频率偏差。

随着系统频率恢复到准稳态，df/dt逐渐减少为零。70s后，采用传统下垂控制和改进下垂控制策略时，DFIG注入电网的有功功率相同[图8（b）]。由于本文侧重于研究DFIG调频性能，未考虑风电机组转速恢复，从图8（c）可知，随着频率响应结束，风机转速逐渐收敛。

4.2 场景2

为进一步验证改进下垂控制策略在大功率扰动下的有效性，将场景2中的扰动大小调整为130MW。仿真结果如图9所示。

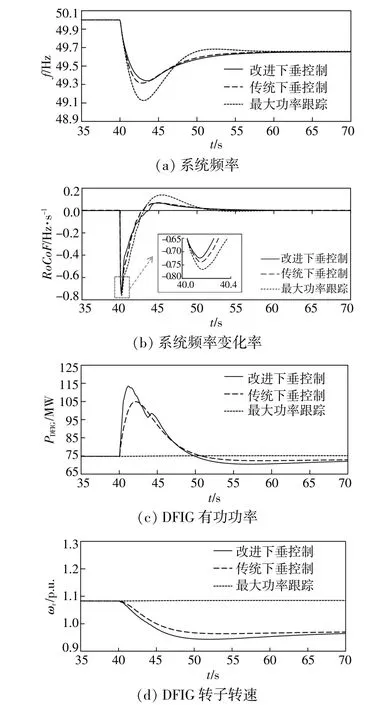
图9 场景2的仿真结果Fig.9 Simulation results for Case2

由于系统动态频率特性和负荷扰动呈正相关，当DFIG不参与系统调频时，电网频率最低点和最大频率变化率分别为49.125Hz和-0.758 Hz/s，明 显 低 于 场 景1。由 图9（a）可 知，当DFIG采用传统下垂控制和改进的下垂控制策略时，系统最大频率偏差分别为0.685，0.661Hz，最大频率变化率分别为-0.735，-0.723Hz/s。与传统下垂控制相比，采用改进下垂控制时，系统最大频率偏差和最大频率变化率分别减少了0.024Hz，0.012 Hz/s，有效提升了电网频率的稳定性。这是因为采用改进下垂控制时，DFIG在频率响应初期，释放了更多的转子动能，为电网注入了更大的补偿功率[图9（c）和 图9（d）]。

对比场景1和场景2的仿真结果可见，在扰动分别为70MW和130MW的情况下，与传统下垂控制策略相比，采用改进的下垂控制后，电网最大频率偏差分别改善了0.011，0.024Hz，最大频率变化率分别改善了0.011，0.012Hz/s。由此可见，随着扰动的增大，改进的下垂控制具有更好的调频效果。两个场景中不同控制策略下的调频效果对比如表1所示。

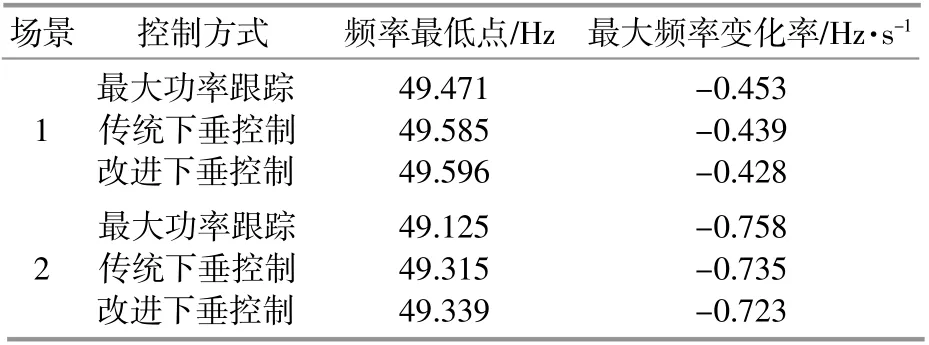
表1 两个场景中不同控制策略下的调频效果对比Table1 Comparison of frequency regulation effects with different control strategies in two scenarios

5 结论

本文提出了一种基于改进下垂控制的DFIG频率控制策略，实现了DFIG自适应调频。

本文提出的计及系统频率变换率（RoCoF）的下垂控制系数整定方法，使风机下垂控制增益能够随着系统频率实时变化状态进行自适应调节，有效地提高了不同扰动下DFIG的频率支撑能力。

在频率扰动初期，基于较大的系统频率变化速率，DFIG采用改进后的下垂控制策略，获得一个更优且与系统频率状态相耦合的下垂增益；进而可更加充分地利用转子动能，为电网提供更多的功率支撑；有效缓解了系统频率跌落的速度和深度；在一定程度上弥补了传统下垂控制的局限性。

仿真结果表明，本文提出的控制策略能够更好地激发风电机组的调频潜力，进一步改善扰动后的系统最大频率变化率和最大频率偏差，提高了系统频率稳定性。