山地城市地铁制动/轨道结构参数对钢轨波磨的影响

崔晓璐，尹越，包鹏羽，唐传平，漆伟

山地城市地铁制动/轨道结构参数对钢轨波磨的影响

崔晓璐1,2，尹越1，包鹏羽1，唐传平1，漆伟2

（1.重庆交通大学 机电与车辆工程学院，重庆 400074；2.重庆市轨道交通（集团）有限公司，重庆 401120）

山地城市地铁相较于平原城市地铁具有爬坡大且曲线多的复杂线路特点，其钢轨波磨问题更加严重。探究山地城市地铁制动区间钢轨波磨的形成机理，提出相应钢轨波磨的控制方法。首先，结合现场调研建立了轮对-轨道-制动系统的有限元模型。然后，采用复特征值分析法研究了轮对-轨道-制动系统的摩擦自激振动特性，进而对制动闸片的表面织构及扣件参数进行参数化分析。最后，基于最小二乘法，采用2种拟合方程对扣件参数进行多参数拟合，并采用遗传算法与粒子群算法确定抑制钢轨波磨扣件参数的最优解。发现轮对-轨道-制动系统存在2个不稳定振动频率，分别为653.73 Hz与584.76 Hz，其中653.73 Hz的复特征值实部较大，为46.53。对比不同表面织构，采用正六边形织构表面闸片的轮对-轨道-制动系统复特征值实部最小，为19.46。对比扣件参数优化前后，采用优化后的扣件参数的轮对-轨道-制动系统复特征值实部较小，为0.49。轮轨子系统与制动子系统的摩擦耦合作用导致轮对-轨道-制动系统摩擦自激振动，是诱导山地城市地铁制动区间钢轨波磨产生的重要因素。当采用正六边形表面织构闸片或设置扣件参数中垂向刚度为36.2 MN/m，垂向阻尼为2 800 N·s/m，横向刚度为25 MN/m，横向阻尼为2 000 N·s/m时能有效抑制钢轨波磨的产生。

钢轨波磨；摩擦自激振动；复特征值分析；表面织构；扣件优化；粒子群法

地铁作为一种重要的城市交通运输方式，因其方便快捷等特点受到广泛应用。随着地铁运行环境逐渐多样化，普通国产的A、B、C型地铁不能满足所有地区的运行要求，尤其是线路复杂的西南山地城市，在线路纵断面设计时，为缩短线路长度，常常会采用长大坡道，最大坡度可采用4%。在平面曲线设计时，由于地形限制有些区段圆曲线半径小于300 m。“山城”重庆是典型的山地城市，根据重庆长大坡道多、转弯半径小的线路特点设计出As型地铁。As 型地铁列车是基于A型与B型地铁，通过优化车辆参数和动力配置，大幅度提高爬坡与转弯性能，最大坡道可达5%，正线最小半径可达250 m。因此，重庆地铁对于山地城市地铁的研究具有一定代表性。随着地铁运行时间的增长，地铁钢轨上出现了波磨、侧磨、擦伤、凹坑等各种损伤问题，造成了巨大的经济损失[1-2]。钢轨波磨作为显著的轮轨损伤问题之一，它是一种在钢轨表面上出现的周期性波浪形不平顺缺陷，会影响列车运行的平稳性与安全性。目前可以采用打磨、更换钢轨和改变列车通过速度等方法抑制钢轨波磨的产生，但列车运行一段时间后钢轨波磨又会重新出现，不能完全根除[3-4]。

为彻底消除钢轨波磨，许多学者对钢轨波磨的产生机理开展了系列研究。夏晨光等[5]基于轮轨摩擦自激振动诱导钢轨波磨理论，建立了轮对-钢轨-轨枕-车轮辐板涂层的有限元模型，发现了涂层的阻尼系数对钢轨波磨的影响规律。闫硕等[6]基于轮轨振动理论，建立了内轮-低轨系统的有限元模型，探究了轮轨接触角和牵引角对钢轨波磨的影响特性。李响等[7]通过建立车辆-轨道系统的动力学模型，研究了车辆运行速度与轨道超高设置对钢轨波磨的影响规律。Zhang等[8]通过现场锤击试验测定了轨道结构的固有特性，并考虑科隆蛋等多种轨道结构，研究了北京地铁钢轨波磨现象。Wu等[9]基于轮轨摩擦自激振动理论，建立了先锋扣件-导向轮对-轨道系统的有限元模型，对扣件橡胶垫及浮置板下橡胶垫的参数进行参数化分析，并提出钢轨波磨的抑制方法。Xiao等[10]基于轮轨振动理论，建立了多种轨道结构的轮轨系统有限元模型与动力学模型，从频域和时域的角度探究了轨道结构固有特性与钢轨波磨的关联规律。Meehan等[11]建立了钢轨波磨的增长模型，发现了列车速度对钢轨波磨增长的影响规律。Correa等[12]建立了4种轨道类型的有限元模型，并考虑多种列车速度和轨道半径，研究了钢轨波磨的增长趋势。Oyarzabal等[13]建立了不同轨道结构的有限元模型，并考虑转向架4个车轮与轨道的相互作用，研究了钢轨波磨的增长趋势并以此进行排序。

根据钢轨波磨形成机理的研究综述[14-17]，钢轨波磨的产生受到轨道结构、车辆参数、列车运行环境等多因素影响，钢轨波磨的形成机理也各不相同。上述研究仅考虑轮轨摩擦自激振动理论，分析了小半径曲线区段处钢轨波磨的形成机理，并不能解释山地城市地铁长大下坡制动区间钢轨波磨的形成机理。由于列车在长大坡道运行时，轮轨间的蠕滑作用会导致轮轨系统的摩擦自激振动，制动装置的滚滑作用会导致制动系统的摩擦自激振动。因此，本文综合考虑了轮轨系统摩擦自激振动和制动系统摩擦自激振动的综合影响，探究了山地城市地铁长大坡道制动区间的钢轨波磨的形成机理，并从优化制动与轨道结构参数的角度，在制动系统中引用表面织构的优化方式，在轨道系统中考虑扣件多参数的共同作用，提出了该区段钢轨波磨的控制方法。

1 山地城市地铁线路钢轨波磨的现场调研

本文以重庆市轨道交通十号线为调研对象，现场调研发现在列车制动区间频繁出现钢轨波磨。该路线的轨道支撑结构为弹性长轨枕，采用60 kg/m钢轨。该线路的运行车辆为As型铝合金车辆，列车单元由5动1拖组成，最高速度为100 km/h，其动车与拖车的制动装置均采用轮盘制动，轮对为直辐板磨耗型踏面轮对。

本文选取了重庆市轨道交通十号线三亚湾-民心佳园的制动区间作为局部调研对象。该制动区间为直线段，坡度为‒2%，轨距为1 435 mm，1/40轨底坡，采用DTVI2型扣件，扣件间距为625 mm，地铁列车在该区间行驶速度为80～100 km/h。根据局部现场调研的结果，发现制动区间2条钢轨上均出现波长为40～50 mm的钢轨波磨，其中一侧的钢轨波磨情况如图1所示。根据钢轨波磨的波长、诱导钢轨波磨的频率与通过列车速度的关系式（1）[18]，可得诱导钢轨波磨产生的频率范围为444.44～694.44 Hz。

式中：为诱导钢轨波磨的频率，Hz；为通过列车速度，m/s；为钢轨波磨的波长，m。

图1 山地城市地铁制动区间的钢轨波磨

Fig.1 Rail corrugation in braking section of mountain city metro

2 山地城市地铁线路钢轨波磨的数值仿真

2.1 轮对-轨道-制动系统的接触模型

结合现场调研可得到轮对-轨道-制动系统的接触模型，如图2所示。该接触模型主要包括轮轨接触子系统和制动接触子系统。对于轮轨接触子系统，当列车通过制动区间时，左右轮受到转向架的垂向悬挂力分别为SVL、SVR，受到左右轨的法向力分别为L、R，切向力分别为L、R，左右轮与钢轨的接触角分别为L、R。左右轨通过扣件与弹性长轨枕相连，垂向刚度分别为VL、VR，垂向阻尼分别为VL、VR，横向刚度分别为L、R，横向阻尼分别为L、R。弹性长轨枕接地，垂向刚度为F，垂向阻尼为F。对于制动接触子系统，在制动杠杆受力处施加制动力，制动杠杆与制动托连接，制动闸片固定在制动托上，制动闸片与制动盘接触，制动盘安装在轮对辐板上。

图2 轮对-轨道-制动系统的接触模型

2.2 轮对-轨道-制动系统的有限元模型

根据轮对-轨道-制动系统的接触模型，运用ABAQUS有限元软件建立轮对-轨道-制动系统的有限元模型，如图3所示。该模型包括了轮轨子系统和制动子系统。轮轨子系统由轮对、扣件、钢轨和弹性长轨枕组成，制动子系统由制动闸片、制动托、制动杠杆与制动盘组成，相关部件参数如表1—2所示。对于轮轨子系统，轮对滚动圆直径为840 mm，在车轴两端设置约束，同时在车轴左右两端分别施加75 kN悬挂力[19]。钢轨轨距为1 435 mm，且钢轨两端设置约束。钢轨与轮对设置面与面接触，摩擦因数为0.4[20]，钢轨接触面采取了细化措施。钢轨通过DTVI2型扣件与弹性长轨枕连接，扣件间隔为625 mm，采用点对点弹簧阻尼单元模拟扣件[21]。弹性长轨枕底部接地，采用点对地弹簧阻尼单元模拟，为了降低钢轨两端约束产生的边界效应，弹性长轨枕共选用30跨。对于制动子系统，在制动杠杆受力处施加制动力10 kN[19]，在制动杠杆支点以及制动杠杆与制动托的连接处设置铰链约束，制动盘与制动闸片之间的摩擦因数为0.4[19]。

图3 轮对-轨道-制动系统的有限元模型

2.3 复特征值法

基于摩擦自激振动诱导钢轨波磨的理论，本文采用复特征值分析法研究了山地城市地铁制动区间轮对-轨道-制动系统的摩擦自激振动特性。复特征值法是一种稳态系统分析方法，在频域范围内预测系统稳定性，轮轨系统的运动方程为[22]：

表1 轮对-轨道-制动系统有限元模型部件参数[19-20]

表2 轨道支撑结构刚度和阻尼[19-20]

式中：为质量矩阵；为阻尼矩阵；为刚度矩阵；为节点位移；为作用于系统的广义外力矢量。=Kf，其中为轮轨间的摩擦因数，f为轮轨摩擦刚度矩阵，代入式（2）得到轮轨系统的运动方程与特征方程，见式（3）—（4）。

式中：与分别为原始空间的复特征值与特征向量；‒Kf为非对称刚度矩阵，求解需要采用子空间投影法，得到投影空间中轮轨系统的运动方程，见式（5）。

式中：*、*、*分别为投影后的质量矩阵、阻尼矩阵和刚度矩阵；为模态坐标向量。与的关系式为=r，r为变化矩阵，得到投影空间中轮轨系统的特征方程为：

使用标准QZ方法求解方程组，得到投影空间的复特征值p和特征向量p，再将p投影到原始空间，得到原始空间的特征向量，则原始系统通解可由单个特征模态叠加而来：

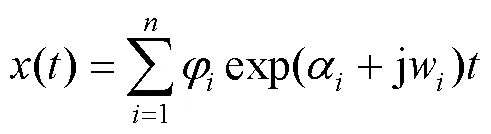
式中：为时间；为复特征阶数，为系统第阶复特征值，=+jw；为复特征值实部；w为复特征值虚部。当复特征值的实部为负值时，系统趋于稳定，当实部为正值时，系统趋于不稳定，并且实部越大，系统发生不稳定振动的可能性越大[23]。文中采用复特征值分析法研究轮对-轨道-制动系统的摩擦自激振动特性，通过比较轮对-轨道-制动系统复特征值实部，判断轮对-轨道-制动系统产生摩擦自激振动的可能性。

3 结果与讨论

3.1 轮对-轨道-制动系统摩擦自激振动特性分析

山地城市地铁线路的显著特点是长大坡道较多。列车在长大坡道运行时，轮轨子系统中轮轨间的蠕滑力趋于饱和，轮轨间的黏滑作用可能会诱导轮轨子系统的摩擦自激振动。另外，列车处于制动工况时，此时制动子系统中制动闸片与制动盘的滚滑作用可能会诱导制动子系统的摩擦自激振动。本文综合考虑了山地城市地铁长大坡道区间制动工况时轮轨子系统的黏滑作用和制动子系统的滚滑作用，采用复特征值分析法探究了轮对-轨道-制动系统中轮轨子系统和制动子系统的摩擦耦合作用对整个系统摩擦自激振动特性的影响，如图4所示。研究发现，轮对-轨道-制动系统存在2个不稳定的振动频率，分别为653.73 Hz与584.76 Hz，对应模态中2条钢轨均产生不稳定振动，其中653.73 Hz对应的复特征值实部较大，为46.53。由复特征值分析法可知，复特征值实部越大，系统发生摩擦自激振动的可能性越大，所以本文重点关注653.73 Hz不稳定振动频率。结果表明，轮轨子系统与制动子系统的摩擦耦合作用会导致轮对-轨道-制动系统的摩擦自激振动，且轮对-轨道-制动系统发生摩擦自激振动的频率与现场诱导钢轨波磨的频率相近，这意味着轮轨子系统与制动子系统的摩擦耦合作用是诱导山地城市地铁制动区间钢轨波磨产生的重要因素。

图4 轮对-轨道-制动系统复特征值实部及相应模态

3.2 制动区段钢轨波磨问题控制方法研究

本节通过对制动子系统和轮轨子系统的优化，实现对轮对-钢轨-制动系统摩擦自激振动的抑制，提出山地城市地铁制动区间钢轨波磨的控制方法。在制动子系统中，研究了制动闸片的表面织构对整个系统摩擦自激振动特性的影响规律。在轮轨子系统中，对扣件参数进行参数化分析，并综合采用不同拟合方程及优化算法确定扣件参数的最优解。

3.2.1 制动闸片的表面织构对轮对-轨道-制动系统摩擦自激振动特性的影响规律

前期研究表明制动闸片的表面织构有助于打断制动闸片和制动盘间的滚滑作用，在一定程度上可以抑制制动系统的摩擦自激振动[24]。本节结合前文中轮对-轨道-制动系统的有限元模型，探究了制动闸片的表面织构对整个轮对-轨道-制动系统摩擦自激振动特性的影响规律。制动闸片的表面织构是一种具有一定尺寸和排列的图案阵列，常见的表面织构以不同形状和分布的凹坑和槽形为主[25]。为了研究制动闸片的表面织构对轮对-轨道-制动系统摩擦自激振动的影响，本节选用了3种表面织构闸片[26]，得到不同表面织构闸片的复特征值实部、相应模态及闸片接触应力，如图5所示。研究发现采用不同表面织构闸片时，轮对-轨道-制动系统发生摩擦自激振动的主要频率仍约为650 Hz。首先，对比有无表面织构的闸片，发现有表面织构闸片的系统复特征值实部更小，表明在制动闸片上引入表面织构能一定程度抑制钢轨波磨的产生。进而对比不同表面织构的闸片，发现采用正六边形织构表面闸片的系统复特征值实部最小，为19.46，且相较于其他闸片，其最大接触应力最小。结果表明，正六边形表面织构抑制钢轨波磨的效果最好。

3.2.2 扣件参数对轮对-轨道-制动系统摩擦自激振动特性的影响规律

扣件是轮轨系统中降噪减振的重要部件，对轮轨子系统摩擦自激振动特性存在重要影响[27]。本节结合前文中轮对-轨道-制动系统的有限元模型，采用控制变量法研究了扣件垂向刚度、扣件垂向阻尼、扣件横向刚度和扣件横向阻尼4个参数对轮对-轨道-制动系统摩擦自激振动特性的影响规律[28]。本节选取扣件垂向刚度的变化范围为5～45 MN/m，扣件横向刚度的变化范围为5～25 MN/m，扣件垂向阻尼的变化范围为2 800～10 000 N·s/m，扣件横向阻尼的变化范围为1 200～2 000 N·s/m[20]。首先，对各扣件参数的无量纲值做归一化处理并作为取值变量，且各扣件参数取值间隔为0.25。选取DTVI2型扣件的参数初始值为控制变量，并将其复特征值实部46.53作为参考线（即图6中虚线）。改变某单一变量，保持其他变量不变，得到扣件参数对轮对-轨道-制动系统摩擦自激振动特性的影响规律，如图6所示。研究发现，以扣件垂向刚度作为变量，其复特征值实部先逐渐减小，当变量大于0.75（即扣件垂向刚度大于35 MN/m）后，复特征值实部增大。以扣件横向刚度作为变量，复特征值实部随变量增大而减小。以扣件垂向阻尼或横向阻尼作为变量，复特征值实部随变量增大变化较小。对比4种扣件参数，发现扣件的垂向刚度与横向刚度对轮对-轨道-制动系统摩擦自激振动特性的影响较大。结果表明，在一定范围内减小垂向刚度和增大横向刚度可以抑制钢轨波磨的产生。

图5 不同表面织构闸片轮对-轨道-制动系统的复特征值实部、相应模态及闸片接触应力

图6 扣件参数对轮对-轨道-制动系统摩擦自激振动特性的影响规律

通过控制变量法可以得到扣件单个参数对轮对-轨道-制动系统摩擦自激振动特性的影响规律，为进一步研究多参数间的相互作用对整个系统摩擦自激振动特性的影响规律，并确定扣件参数的最优解。首先，采用最小二乘法对扣件的垂向刚度、垂向阻尼、横向刚度和横向阻，4个参数进行拟合，本节选用2种拟合方程并相互验证，2种拟合方程的对比如表3所示。拟合方程Ⅰ中，1、2、3、4分别表示扣件垂向刚度、扣件垂向阻尼、扣件横向刚度和扣件横向阻尼4种参数的取值；2、3、4分别是2、3、4经过一元拟合及收缩得到的影响系数；(1)、(2)、(3)为方程的未知系数，可通过最小二乘法计算得到。1为46.53，是作为控制变量的DTVI2型扣件参数的初始值对应的复特征值实部。拟合方程Ⅱ中，1、2、3、4经过一元拟合后获得* 1、* 2、* 3、* 4，b为回归方程中多项式的未知系数。其中拟合方程Ⅰ的均方根误差为3.99，如图7a所示，拟合方程Ⅱ的均方根误差为4.39，如图7b所示，表明2种拟合方程的预测值与复特征实部的吻合性较好。

采用遗传算法与粒子群算法分别对2种拟合方程求最优解，并相互验证。2种优化算法的对比结果如表4所示。采用遗传算法时，每种扣件参数的取值区间为0～1，取值精度为0.01。采用粒子群算法时，选择粒子位置最大值为1，选择位置最小值为0，粒子初始速度最大值为1，粒子初始速度最小值为‒1。

表3 2种拟合方程的对比

图7 拟合方程的误差分析

表4 2种优化算法的对比

最后通过2种拟合方程与2种优化算法得到4组相近的优化结果，将4组优化结果通过求平均值或取相同值等数据处理，得到扣件参数最优解[0.78, 0, 1, 1]，即扣件垂向刚度为36.2 MN/m，扣件垂向阻尼为2 800 N·s/m，扣件横向刚度为25 MN/m，扣件横向阻尼为2 000 N·s/m。对比扣件参数优化前后，采用优化后的扣件参数的系统复特征值实部较小，为0.49，如图8所示。结果表明，优化后的扣件参数能有效抑制钢轨波磨的产生。

4 结论

1）轮轨子系统与制动子系统的摩擦耦合作用导致轮对-轨道-制动系统摩擦自激振动，是诱导山地城市地铁制动区间钢轨波磨产生的重要因素。

2）制动闸片的表面织构能一定程度抑制钢轨波磨的产生，且正六边形表面织构闸片的抑制效果最好。

3）当扣件垂向刚度为36.2 MN/m、扣件垂向阻尼为2 800 N·s/m、扣件横向刚度为25 MN/m、扣件横向阻尼为2 000 N·s/m时，能有效抑制钢轨波磨的产生。

[1] 朱海燕, 袁遥, 肖乾, 等. 钢轨波磨研究进展[J]. 交通运输工程学报, 2021, 21(3): 110-133.

ZHU Hai-yan, YUAN Yao, XIAO Qian, et al. Research Progress of Rail Corrugation[J]. Journal of Traffic and Transportation Engineering, 2021, 21(3): 110-133.

[2] 关庆华, 张斌, 熊嘉阳, 等. 地铁钢轨波磨的基本特征、形成机理和治理措施综述[J]. 交通运输工程学报, 2021, 21(1): 316-337.

GUAN Qing-hua, ZHANG Bin, XIONG Jia-yang, et al. Review on Basic Characteristics, Formation Mechanisms, and Treatment Measures of Rail Corrugation in Metro Systems[J]. Journal of Traffic and Transportation Engi­neering, 2021, 21(1): 316-337.

[3] CHEN Guang-xiong. Friction-Induced Vibration of a Railway Wheelset-Track System and Its Effect on Rail Corrugation[J]. Lubricants, 2020, 8(2): 18.

[4] CHEN G X, ZHANG S, WU B W, et al. Field Measure­ment and Model Prediction of Rail Corrugation[J]. Pro­ceedings of the Institution of Mechanical Engineers, Part F: Journal of Rail and Rapid Transit, 2020, 234(4): 381-392.

[5] 夏晨光, 陈光雄, 朱旻昊, 等. 车轮辐板阻尼涂层对钢轨波磨的影响[J]. 表面技术, 2020, 49(3): 134-140.

XIA Chen-guang, CHEN Guang-xiong, ZHU Min-hao, et al. Effect of Damped Coating of Wheel Web on Rail Cor­rugation[J]. Surface Technology, 2020, 49(3): 134-140.

[6] 闫硕, 赵晓男, 崔晓璐, 等. 轮轨接触参数对钢轨波磨的影响[J]. 润滑与密封, 2018, 43(11): 42-46.

YAN Shuo, ZHAO Xiao-nan, CUI Xiao-lu, et al. Influen­ce of Wheel/Rail Contact Parameters on Rail Corruga­tion[J]. Lubrication Engineering, 2018, 43(11): 42-46.

[7] 李响, 任尊松, 徐宁. 地铁小半径曲线段钢弹簧浮置板轨道的钢轨波磨研究[J]. 铁道学报, 2017, 39(8): 70-76.

LI Xiang, REN Zun-song, XU Ning. Study on Rail Corru­gation of Steel Spring Floating Slab Track on Subway with Small Radius Curve Track[J]. Journal of the China Railway Society, 2017, 39(8): 70-76.

[8] ZHANG Hou-gui, LIU Wei-ning, LIU Wei-feng, et al. Study on the Cause and Treatment of Rail Corrugation for Beijing Metro[J]. Wear, 2014, 317(1-2): 120-128.

[9] WU B W, CHEN G X, LV J Z, et al. Generation Me­chanism and Remedy Method of Rail Corrugation at a Sharp Curved Metro Track with Vanguard Fasteners[J]. Journal of Low Frequency Noise, Vibration and Active Control, 2020, 39(2): 368-381.

[10] XIAO Hong, YANG Song, WANG Hao-yu, et al. Initia­tion and Development of Rail Corrugation Based on Track Vibration in Metro Systems[J]. Proceedings of the Institution of Mechanical Engineers, Part F: Journal of Rail and Rapid Transit, 2018, 232(9): 2228-2243.

[11] MEEHAN P A, BATTEN R D, BELLETTE P A. The Effect of Non-Uniform Train Speed Distribution on Rail Corrugation Growth in Curves/Corners[J]. Wear, 2016, 366-367: 27-37.

[12] CORREA N, OYARZABAL O, VADILLO E G, et al. Rail Corrugation Development in High Speed Lines[J]. Wear, 2011, 271(9-10): 2438-2447.

[13] OYARZABAL O, CORREA N, VADILLO E G, et al. Modelling Rail Corrugation with Specific-Track Para­meters Focusing on Ballasted Track and Slab Track[J]. Vehicle System Dynamics, 2011, 49(11): 1733-1748.

[14] GRASSIE S L. Rail Corrugation: Advances in Measure­ment, Understanding and Treatment[J]. Wear, 2005, 258(7-8): 1224-1234.

[15] TANAKA H, MIWA M. Modeling the Development of Rail Corrugation to Schedule a more Economical Rail Grinding[J]. Proceedings of the Institution of Mechanical Engineers, Part F: Journal of Rail and Rapid Transit, 2020, 234(4): 370-380.

[16] GRASSIE S L. A Practical Methodology to Prioritise Reprofiling Sites for Corrugation Removal[J]. Procee­dings of the Institution of Mechanical Engineers, Part F: Journal of Rail and Rapid Transit, 2020, 234(4): 362-369.

[17] SATO Y, MATSUMOTO A, KNOTHE K. Review on Rail Corrugation Studies[J]. Wear, 2002, 253(1-2): 130-139.

[18] 李伟. 地铁钢轨波磨成因及其对车辆/轨道行为的影响[D]. 成都: 西南交通大学, 2015.

LI Wei. Study on Root Cause of Metro Rail Corrugation and Its Influence on Behavior of Vehicle-Track Sys­tem[D]. Chengdu: Southwest Jiaotong University, 2015.

[19] 吴波文. 制动对车轮多边形磨耗和钢轨波磨影响的研究[D]. 成都: 西南交通大学, 2020.

WU Bo-wen. Research on the Effect of Brake on Wheel Polygonal Wear and Rail Corrugation[D]. Chengdu: Sou­th­west Jiaotong University, 2020.

[20] CUI Xiao-lu, HUANG Bo, DU Zi-xue, et al. Study on the Mechanism of the Abnormal Phenomenon of Rail Corru­gation in the Curve Interval of a Mountain City Metro[J]. Tribology Transactions, 2020, 63(6): 996-1007.

[21] 赵晓男, 陈光雄, 崔晓璐, 等. 高速列车车轮多边形磨耗的形成机理及影响因素探究[J]. 表面技术, 2018, 47(8): 8-13.

ZHAO Xiao-nan, CHEN Guang-xiong, CUI Xiao-lu, et al. Formation Mechanism and Influencing Factors of the Polygonal Wear of High-Speed Train Wheels[J]. Surface Technology, 2018, 47(8): 8-13.

[22] EL BESHBICHI O, WAN C, BRUNI S, et al. Complex Eigenvalue Analysis and Parameters Analysis to Inves­tigate the Formation of Railhead Corrugation in Sharp Curves[J]. Wear, 2020, 450-451: 203150.

[23] ABUBAKAR A R, OUYANG Hua-jiang. Complex Ei­gen­value Analysis and Dynamic Transient Analysis in Predicting Disc Brake Squeal[J]. International Journal of Vehicle Noise and Vibration, 2006, 2(2): 143.

[24] 朱章杨, 莫继良, 王东伟, 等. 沟槽对界面振动及摩擦磨损特性的影响[J]. 摩擦学学报, 2017, 37(4): 551-557.

ZHU Zhang-yang, MO Ji-liang, WANG Dong-wei, et al. Effect of Groove on Interface Vibration and Friction and Wear Behaviors[J]. Tribology, 2017, 37(4): 551-557.

[25] 张青, 崔晓璐, 陈光雄, 等. 沟槽织构对盘形制动噪声的影响[J]. 机械设计, 2017, 34(2): 62-67.

ZHANG Qing, CUI Xiao-lu, CHEN Guang-xiong, et al. Effect of Groove-Texture on Disc Braking Noise[J]. Jour­nal of Machine Design, 2017, 34(2): 62-67.

[26] ZHU Q, CHEN G X, WU B W, et al. Effect of the Ma­terial Parameter and Shape of Brake Pads on Friction- Induced Disc Brake Squeal of a Railway Vehicle[J]. Tribology Transactions, 2021, 64(4): 744-752.

[27] 朱宁, 杨新文, 赵治均. 地铁线路扣件刚度对钢轨振动与波磨的影响[J]. 计算机辅助工程, 2021, 30(3): 49-54.

ZHU Ning, YANG Xin-wen, ZHAO Zhi-jun. Influence of Rail Fastening Stiffness of Metro Line on Rail Admit­tance and Rail Corrugation[J]. Computer Aided Enginee­ring, 2021, 30(3): 49-54.

[28] 赵江伟, 赵晓男, 陈光雄, 等. 地铁小半径曲线轨道扣件参数对钢轨波磨的影响[J]. 铁道标准设计, 2018, 62(12): 6-10.

ZHAO Jiang-wei, ZHAO Xiao-nan, CHEN Guang-xiong, et al. Effect of Fastener Parameters on Rail Corrugation of Metro Tight Curve Track[J]. Railway Standard Design, 2018, 62(12): 6-10.

Effect of the Structure and Parameter of Brake/Track on Rail Corrugation in a Mountain City Metro

1,2,1,1,1,2

(1. School of Mechanotronics & Vehicle Engineering, Chongqing Jiaotong University, Chongqing 400074, China; 2. Chongqing Rail Transit (Group) Co., Ltd., Chongqing 401120, China)

Compared with flat city metro, mountain city metro has the characteristics of complex lines with large climbing slopes and many curves. Its rail corrugation forms are more diverse. This paper is aimed at exploring the generation mechanism of rail corrugation in braking section of mountain city metro, and proposing relevant control method of rail corrugation. Based on the theory that rail corrugation is induced by friction self-excited vibration, the rail corrugation in braking section of mountain city metro is studied. Firstly, according to the field investigation of Chongqing Rail Transit Line 10, it is found that the rail corrugation with wavelength of 40-50 mm occurs frequently in braking section of mountain city metro. After that, combined with the field investigation, the contact model of the wheelset-track-brake system is obtained. According to the contact model of the wheelset-track-brake system, the finite element model of the wheelset-track-brake system is built. Then, the friction self-excited vibration characteristics of the wheelset-track-brake system are studied by complex eigenvalue analysis method. Furthermore, the influence of fastener parameters and surface texture of brake pad on the friction self-excited vibration characteristics of the wheelset-track-brake system is studied. Two fitting equations are applied to fit the fastener parameters by least square method. The root mean square error of fitting equation I is 3.99, and the root mean square error of fitting equation II is 4.39. Based on the two fitting equations, the optimal solution of fastener parameters is obtained by genetic algorithm and particle swarm optimization algorithm. The results show that there are two unstable vibration frequencies of 653.73 Hz and 584.76 Hz in the wheel set-track-brake system. Under the corresponding modes, both rails occur unstable vibration. The real part of the complex eigenvalue of 653.73 Hz is larger, which is 46.53. Comparing surface texture and no surface texture of brake pad, it is found that the real part of the complex eigenvalue of the wheelset-track-brake system with surface texture of brake pad is smaller. Comparing different surface textures of brake pad, the real part of the complex eigenvalue of the wheelset-track-brake system with regular hexagonal texture of brake pad is the smallest, which is 19.46. Comparing four fastener parameters, it is found that vertical stiffness and lateral stiffness of fastener parameters have a great influence on the friction self-excited vibration characteristics of the wheelset-track-brake system. Comparing fastener parameters before and after optimization, the real part of the complex eigenvalue of the wheelset-track-brake system with the optimal solution of fastener parameters is smaller, which is 0.49. In conclusion, the friction between wheelset-rail subsystem and brake subsystem leads to the friction self-excited vibration of the wheelset-track-brake system. And it is an important factor to induce rail corrugation in braking section of mountain city metro. Surface texture of brake pad and Vertical stiffness and lateral stiffness of fastener parameters have obvious effects on the generation of rail corrugation. And rail corrugation can be effectively suppressed, when regular hexagonal surface texture of brake pad is adopted, or when vertical stiffness of fastener is 36.2 MN/m, vertical damping of fastener is 2 800 N·s/m, lateral stiffness of fastener is 25 MN/m, lateral damping of fastener is 2 000 N·s/m.

rail corrugation; friction self-excited vibration; complex eigenvalue analysis; surface texture; fastener optimization; particle swarm optimization

TH117

A

1001-3660(2023)01-0103-09

10.16490/j.cnki.issn.1001-3660.2023.01.011

2021–12–27；

2022–03–27

2021-12-27；

2022-03-27

国家自然科学基金面上项目（52275176）；重庆市教委科学技术研究项目重点项目（KJZD-K202100703）；交通工程应用机器人重庆市工程实验室开放课题（CELTEAR-KFKT-202004）；重庆交通大学研究生科研创新项目（CYS21360）

The National Natural Science Foundation of China General Program (52275176); the Chongqing Municipal Education Commission Science and Technology Research Project Key Project (KJZD-K202100703); the Engineering Application Robot Chongqing Engineering Laboratory Open Project (CELTEAR-KFKT-202004); the Chongqing Jiaotong University Graduate Research and Innovation Project (CYS21360)

崔晓璐（1990—），女，博士，教授，主要研究方向为轮轨摩擦学。

CUI Xiao-lu (1990-), Female, Doctor, Professor, Research focus: wheel-rail tribology.

崔晓璐, 尹越, 包鹏羽, 等. 山地城市地铁制动/轨道结构参数对钢轨波磨的影响[J]. 表面技术, 2023, 52(1): 103-111.

CUI Xiao-lu, YIN Yue, BAO Peng-yu, et al. Effect of the Structure and Parameter of Brake/Track on Rail Corrugation in a Mountain City Metro[J]. Surface Technology, 2023, 52(1): 103-111.

责任编辑：万长清