融合多类型深度迁移学习的电力系统暂态稳定自适应评估

李宝琴，吴俊勇，张若愚，强子玥，覃柳芸，王春明，董向明

（1. 北京交通大学电气工程学院，北京 100044；2. 中国长江三峡集团有限公司科学技术研究院，北京 100038；3. 国家电网公司华中分部，湖北武汉 430077）

0 引言

研究表明，大停电事故的开端往往伴随着暂态稳定的破坏。现代电网规模的不断扩大、新能源接入比例的不断提高，都对电力系统的安全稳定运行提出了新的挑战［1-2］。

现有的暂态稳定评估（transient stability assessment，TSA）方法主要有时域仿真法［3］、直接法［4］和机器学习法［5-11］。时域仿真法是最成熟的TSA方法，其计算精度高，但其求解速度慢。直接法计算速度快，但面对复杂电网时不易确定能量函数。与传统的TSA 方法相比，机器学习法从模式识别的角度出发，无需构造复杂的数学解析模型，通过离线学习建立系统特征量与暂稳态预测输出结果间的隐式映射关系，在实际在线应用时，利用学习到的映射关系可快速得出稳定评估结果。常用的浅层学习方法主要有支持向量机（support vector machine，SVM）［5］、决策树（decision tree，DT）［6］、随机森林（random forest，RF）［7］等。由于浅层学习方法对数据挖掘分析的能力有限，在线应用时其泛化能力受到限制。

近年来，随着深度学习方法的快速发展以及由于深度学习方法在特征提取方面的优越性能，其在人脸识别、自然语言处理等领域广泛应用。在电力系统TSA领域：文献［8］提出一种基于深度置信网络（deep belief network，DBN）的TSA 方法，利用深层架构对系统特征与稳定结果之间的映射关系进行训练；文献［9］提出一种基于一维卷积神经网络（convolutional neural network，CNN）的TSA 方法，该方法直接面向底层测量数据，实现了端到端的“时序特征提取+暂态稳定分类”；文献［10］为利用电力系统的时序特征数据，基于长短期记忆网络（long short-term memory，LSTM）算法提出一种基于滑动时间窗口的暂态稳定防抖动模型；文献［11］为降低主动学习过程中选择样本的冗余度，提出一种聚类自适应主动学习选择策略，加快了学习进程。虽然上述深度学习方法在电力系统TSA方面取得了一定的成果，但其忽略了模型的自适应更新能力。数据驱动的TSA 过程是动态变化的，预训练模型需要不断适应电力系统的运行方式或拓扑结构的变化，如负荷水平的大幅波动、发电机或线路的投退等。

迁移学习和深度学习的结合，可有效提升深度学习模型的泛化能力和自适应能力，目前迁移学习在电力系统暂态稳定领域的应用尚处于探索阶段。文献［12］提出一种基于改进深度卷积生成对抗网络的暂态稳定增强型自适应评估方法；文献［13］通过迭代最小化训练数据与未知数据之间边缘分布和条件分布的差异，将预训练模型迁移到未知的不同但相关的故障；文献［14］将基于增量学习的深度继承和基于迁移学习的广度继承应用于暂态稳定预测问题；文献［15］基于CNN，利用新生成的最小平衡样本集训练分类层参数，从而快速得到适用于新场景的预测模型。

综上，为了提高模型的自适应性以及充分发挥不同类型深度学习模型的优势，避免由于单一模型的劣化而导致整个评估系统性能下降，本文将深度学习、迁移学习和故障后的暂态功角稳定评估相结合，提出一种适用于电力系统TSA 的融合多类型深度迁移学习的自适应评估方法，该方法不仅可以自适应地跟踪系统拓扑结构和运行方式的变化，还可以在结构和规模不同的系统之间进行迁移，输出多样性的评估结果，大幅缩短了模型的更新训练时间，实现了电力系统暂态稳定的自适应评估。

1 融合多类型深度学习的TSA模型

1.1 多类型深度学习模型与TSA

暂态稳定预测的本质是求解系统稳定边界［16］，基于机器学习的暂态稳定预测是建立输入特征X和输出Y间的映射关系。原始训练数据集Dpre为：

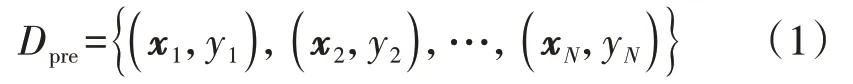
式中：xi∈X∈Rd，yi∈{C1，C2，…，Cm}（i=1，2，…，N），d为输入特征的维度，N为样本总数，Ci(i=1，2，…，m)为暂态稳定预测的第i个类别，m为暂态稳定预测的标签类别数，现有研究大多将暂态稳定看作二分类问题，即m=2，本文将样本分为不稳定样本、较不稳定样本、临界不稳定样本、临界稳定样本、较稳定样本、很稳定样本六大类，因此m=6。本文在判稳的同时进行稳定裕度和失稳程度等级的评估，有效缩短模型的离线训练和在线评估时间。

基于文献［15-17］的研究成果，本文引入轨迹簇的概念，将故障切除后的发电机功角看作一个整体，研究整体的变化规律。轨迹簇特征的定义及计算方法如附录A所示，轨迹簇特征包含基本特征、变化率及曲率、加速度三大类共27 个特征，这些特征将作为各类深度学习模型的输入。轨迹簇特征是发电机功角的统计特征，不会随着系统规模的增大而增加，因此各类深度学习模型的输入节点数始终为27，不受系统网络结构参数的影响。

目前应用于电力系统暂态稳定预测的常用深度学习模型［9-12］为DBN、CNN 和LSTM。DBN 是一种单层之间不连接、层与层之间全连接的基于能量的模型，由于在训练的过程中涉及无监督学习，因此其对标注样本的数量要求较低，可以降低数据标注的成本，但是其难以有效利用不同时间断面之间的时序联系；CNN 通过一系列特征矩阵和卷积核进行卷积计算，最终得到高层特征用于分类，其在学习的过程中共享卷积核，计算量相对较小，但是池化层会丢失部分有价值的信息；LSTM 擅于处理时间序列的数据，深度挖掘不同数据之间的时序特性，但是随着时间跨度增加，计算量也会增大。

针对TSA 问题：CNN 在训练过程中忽略局部和整体间的关联性，其评估结果偏风险；LSTM 充分挖掘时序特性，其评估结果偏保守；DBN具有强大的特征提取和数据挖掘能力，其评估性能适中。由此可见，各类深度学习模型各有优劣，很难有一种模型在所有工况下都始终表现良好。上述3 种深度学习模型的原理及训练算法均已相当成熟，此处不再赘述。

值得说明的是，电力系统在绝大多数情况下都处于稳定运行的状态，因此用于模型训练的稳定样本数远多于失稳样本数，此外，失稳样本漏判和稳定样本误判的代价往往不同。为了解决各类样本数不均衡的问题，本文对各类深度学习模型的损失函数进行改进，采用加权的交叉熵损失函数，加权过程为：

1.2 融合模型的建立

根据暂态稳定分析的特性，输入数据是由相量测量单元（phase measurement unit，PMU）采集的不同时刻的各类电气数据，该数据为流式数据，因此需要有效挖掘不同数据之间的时序特性和联系。若故障切除后系统失稳，则必须快速给出评估结果，从而给紧急控制留出充足的时间，这就要求TSA 模型必须同时满足高精度、高可靠性和快速性的要求，而单一模型往往无法同时满足这些要求。

鉴于目前对模型的选择并没有固定的标准，不同模型在处理同一问题时各有优劣，因此为了解决不同类型人工智能网络对不同电力系统的适应性不同和评估性能不稳定的问题，本文采用融合多类型深度学习模型（multi-type of deep learning model，mDLM）的集成式概率型评估方法，避免因单一类型评估器性能劣化而导致整个评估系统性能下降。离线建模的流程见附录B图B1，具体步骤如下。

1）样本集的生成。通过时域仿真法生成包含各种运行工况、用于模型训练和测试的大样本数据集，计算稳定裕度／失稳程度指标，并贴上对应的标签。

2）轨迹簇特征的提取及数据预处理。针对故障切除后的发电机功角，按照前文所述方法提取不同时间断面下的轨迹簇特征，并将特征值进行最大最小值归一化处理，缩小不同特征之间的数值差异。

3）多类型网络评估系统。采用逐层寻优的实验方法确定各类模型的最佳结构，逐层选择合适的节点数，直到模型的性能趋于稳定或达到预设值。通过实验发现，各类人工智能网络的最佳结构和最优参数并不唯一，在实际应用中可以在各类模型中均挑选n′个性能良好的结构进行集成，模型总数为n。

4）概率输出集成机制。本文各类深度学习模型的输出层均为softmax 层，将样本x预测为各类别的概率分别设为P(C1|x)、P(C2|x)、…、P(C6|x)。各类别的概率满足式（3）。

2 迁移学习

2.1 迁移学习与模型迁移方案

迁移学习是一种举一反三的能力，使机器在处理新领域（目标域）的问题时能够根据已有领域（源域）训练好的模型和部分数据快速训练出适合新场景的模型。在基于深度学习的TSA 中，离线训练往往是针对特定的运行工况，当电力系统的运行方式或拓扑结构发生较大变化时，测试数据集和训练数据集的分布差异较大，预训练模型性能骤降甚至失效，无法进行在线应用，此时，可利用迁移学习对预训练模型进行更新。

本文对迁移学习的研究主要是讨论基于模型的迁移方法，根据各类深度学习模型的结构和特点，本文采用如下3种方案。

方案1：重新训练。保持原来各类深度学习模型结构不变，利用目标域的新训练集重新训练模型。

方案2：微调分类层。将预训练模型中除分类层以外的结构和参数全部迁移至新模型并冻结，利用目标域下的少量样本微调分类层的权重和偏置。

方案3：微调整个网络。将预训练模型的所有结构和参数全部迁移至新模型，将其作为目标域模型的初始值，在此基础上利用目标域下的少量样本微调整个网络的权重和偏置。

2.2 融合迁移学习的多类型深度学习模型的构建

为了避免单一机器学习方法无法有效地表达电力系统故障发展的时间顺序以及难以构建复杂的函数模拟系统运行特征与稳定状态输出结果之间的映射关系，同时针对电力系统的运行方式或拓扑结构发生较大变化时模型评估性能下降的问题，本文在1.2 节融合mDLM 方法的基础上，引入迁移学习，提出一种融合多类型深度迁移学习模型（transfer multi-type of deep learning model，tmDLM）的方法，具体的过程如下。

式中：Transfer(·)表示迁移更新过程。

文献［15］针对暂态稳定二分类预测问题，利用新生成的最小平衡样本集进行迁移。但是对于多分类评估问题而言，变步长加二分法的最小平衡样本集的概念将不再适用，因此，本文的迁移过程是一个不断迭代的过程，采用蒙特卡罗法针对目标域的运行方式或拓扑结构生成少量的样本，设初始迁移样本库Dm为空集，目标域迁移的具体步骤如下。

（1）首先从目标域样本集中随机筛选Nm个样本放入Dm中，并从训练集中将这些样本删除。

（2）利用Dm对原模型M0进行迁移学习，得到新模型M1。

（3）重复以上步骤，每次迭代筛选出Nm个样本，对上一次的模型进行更新微调，直到模型对新场景下的测试集预测准确率达到预设值或迭代过程中模型性能不再提升，此时得到更新后的模型Mnew。在迁移更新的过程中，一般在3～5 次迭代后模型性能可得到有效恢复，大幅减少了目标域所需的样本数量。

3）模型融合。通过1.2 节的基于概率输出的集成机制将迁移后的多类型深度学习模型融合为一个适用于系统当前运行工况和拓扑结构的TSA 模型。值得说明的是，本文所提融合多类型深度迁移学习方法是一种基于模型的迁移，模型迁移的过程中只需保证源域和目标域的输入、输出维度一致即可。针对TSA 问题，本文分类模型的输入为发电机的功角轨迹簇特征，其不会随着系统规模和发电机台数的增加而增加，是统计特征，输入节点数始终是27，为不同系统间基于模型的迁移奠定了基础。此外，本文所构建评估模型的输出节点数为6，在判稳的同时进行稳定裕度和失稳程度等级的评估。因此，源域和目标域系统的输入、输出维度完全一致，可以在结构和规模不同的系统间进行迁移。

2.3 自适应评估流程

完善的基于数据驱动和深度学习模型的TSA包含离线训练、在线评估和周期更新3 个阶段［18］。离线训练好的模型在投入在线评估后需根据系统下一时刻的运行方式或拓扑结构进行周期性的更新。一般情况下，电力系统调度人员会根据负荷预测的结果，通过优化潮流计算安排下一时刻的开停机计划，系统的拓扑结构变化可提前知道，有一定的时间裕度可提前离线生成新场景下的训练样本，并对模型进行迁移更新。3 个阶段的时间联系如附录B 图B2所示。特别地，当系统发生调度人员无法预知的变化时，新样本数可能不足，可以结合样本迁移和样本增强技术［12］，在较短的时间内生成用于模型迁移更新的新样本，从而保证融合模型的持续高精度预测。

融合迁移学习的暂态稳定自适应评估流程见图1，图中Aeval为评估准确率，Acc为判稳准确率。当检测到系统的运行方式或拓扑结构发生变化时，原模型M0的性能下降，立即启动更新过程，使用部分目标域样本集更新M0，得到新模型Mnew用于在线评估。

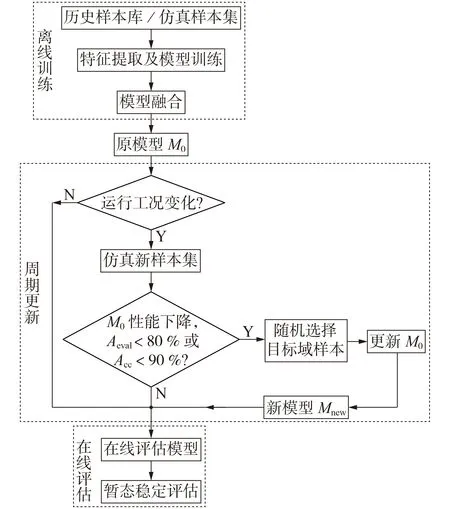
图1 融合迁移学习的暂态稳定自适应评估流程Fig.1 Flowchart of adaptive assessment of transient stability based on transfer learning

2.4 暂态稳定程度评估

2.4.1 稳定程度指标的建立

为了使模型的输出结果更加多样化，本文根据稳定裕度和失稳程度将输出结果划分为6 类，在判稳的同时进行稳定裕度和失稳程度等级的评估，有效缩短模型的离线训练和在线评估的时间，同时减少计算机的存储空间。当系统规模增加时，用于模型训练的样本数大幅增加，此时六分类模型离线训练时间和存储空间的优势将更加凸显。

由于极限切除时间（critical clearing time，CCT）需要通过时域仿真法反复试探得到，因此本文根据文献［19］构造基于转子角轨迹包络线积分的受扰程度S，即发电机转子角轨迹簇所占的面积，将其归一化后得到Bs来评估样本的稳定程度，如式（7）、（8）所示。对于失稳的样本，如果故障切除后经过较长的时间系统才失稳，则预示着有更多的时间来采取进一步的校正控制使系统恢复稳定。因此，本文采用从故障切除到系统发生失稳所经历的时间Bus来评估样本的失稳程度，计算方法如式（9）所示。Bs∈[0，1]，Bus∈[0，5]s，Bs越小，系统的稳定裕度越小，Bus也越小，系统的失稳程度越严重。

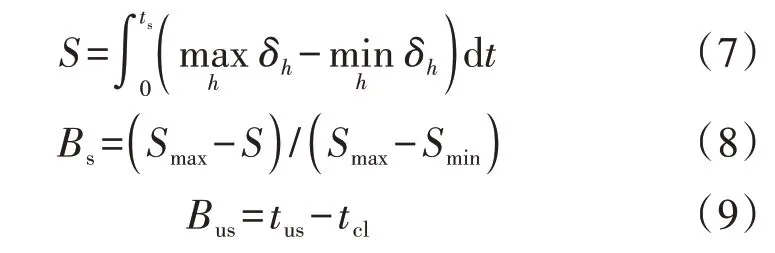
式中：δh为第h台发电机的转子角；ts为仿真时间；Smax、Smin分别为受扰程度S的最大值和最小值；tus为系统发生失稳（即任意2 台发电机的转子角超过360°）的时刻；tcl为故障切除的时刻。

2.4.2 模型性能评价

根据式（7）—（9），按取值范围将样本集进一步划分为6 类，并贴上相应的标签，如表1 所示。表中Bus与Bs的阈值可根据实际电网的运行工况进行调整。离线贴标签时，稳定样本和失稳样本的标签进行分类处理；在线应用时，根据系统的实时响应信息，可以在判稳的同时得到系统的稳定裕度和失稳程度等级，因此不涉及稳定和失稳的先验判别。对于不稳定样本、较不稳定样本和临界不稳定样本，后续采取控制措施的紧急程度不同，具体控制措施以及控制量也不尽相同，对调度人员具有一定的参考意义。

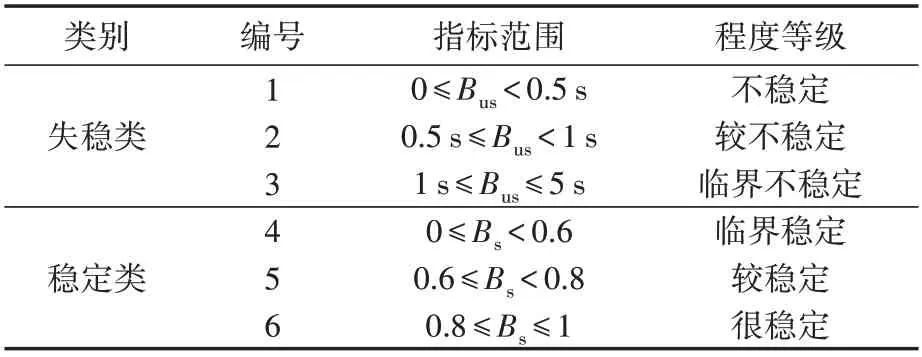
表1 暂态稳定多级指标划分Table 1 Multilevel index division of transient stability

用六分类的数据集来构造多类型的深度学习评估模型，评估结果可以表示为评估结果矩阵R=(rij)6×6，如式（10）所示。其中rij表示实际为第i类而预测为第j类的样本数。定义：Ts、Tus分别表示稳定样本和失稳样本正确识别的数目，分别对应式（10）后3 行的右半部分、前3 行的左半部分；Fus表示将稳定样本误判为失稳样本的样本数，对应式（10）后3行的左半部分；Fs表示将失稳样本漏判为稳定样本的样本数，对应式（10）前3 行的右半部分。由于电力系统暂态稳定是一个典型的非平衡分类问题，因此构建5 个评价指标来评估模型性能，如式（11）—（15）所示。

1）评估准确率Aeval，即正确评估稳定程度等级的样本占所有样本的比例，如式（11）所示。

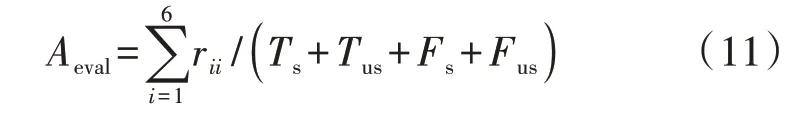
2）判稳准确率Acc，即正确预测稳定／失稳的样本占所有样本的比例，如式（12）所示。

3）安全性Se，即正确预测稳定的样本占所有稳定样本的比例，如式（13）所示。

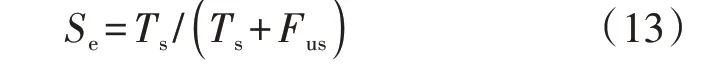
4）可靠性Re，即正确预测失稳的样本占所有失稳样本的比例，如式（14）所示。

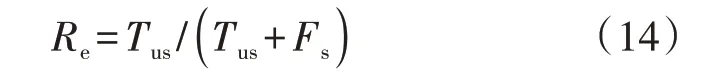
5）可靠性和安全性的几何平均数Gmean，如式（15）所示。与Acc相比，Gmean值能够客观反映模型对失稳样本的预测性能。

3 算例分析

为了验证本文所提融合tmDLM 方法的可行性及有效性，在Tensorflow 环境下搭建和改进DBN、CNN、LSTM 模型，采用Python 编程语言，PC 配置为：Intel（R）Core（TM）i7-8565U CPU／8 GB RAM。

3.1 新英格兰10机39节点系统样本集的生成

新英格兰10 机39 节点系统中包含10 台发电机、39条母线、12台变压器和34条交流线路，额定频率为60 Hz。采用电力系统仿真软件（power system toolbox，PST）3.0 生成暂态稳定样本集。为了构造较为完备的样本空间，考虑系统的常规变化，设置负荷水平为基准负荷的75%～120%，以5%为步长，相应地调整发电机出力以保证潮流收敛。在34 条输电线路上设置最为严重的三相短路故障，故障位置设置在每条输电线路全长的0～90%处，以10%为步长。故障切除时间设置为故障后的1～11 个周期，以1 个周期（即0.016 7 s）为步长。仿真时间为5 s，共生成37400个样本，按4∶1的比例将样本随机划分为训练集和测试集，各类样本的组成见附录B表B1。

3.2 融合多类型模型的性能分析

为了验证本文所提融合mDLM 的性能优势以及融合的必要性，将mDLM 与基分类器DBN、LSTM、CNN 以及浅层学习中的SVM、DT、K 近邻（K nearest neighbor，KNN）进行对比分析。针对以上各分类器，分别选择最优参数［20］。本文各类深度学习模型数n′=1，采用逐层寻优的方式确定性能良好的结构。DBN 的结构为81-200-100-50-30-6，受限玻尔兹曼机（restricted Boltzmann machine，RBM）重构的学习率为0.8；CNN 由输入层、2 对卷积层和池化层、全连接层及分类层组成，其中卷积层的大小为3×3，池化层的大小为2×2，全连接层的节点数为1000，本文直接将暂态稳定样本集分为6 类，因此分类层的节点数为6；LSTM 的结构设置和DBN 的相同，mDLM 的各基分类器均采用Adam 优化算法，初始学习率为0.001，训练样本数为187；SVM 的核函数为径向基函数，采用网格法和五折交叉验证对参数进行寻优；DT采用C5.0算法；KNN经寻优后的最近邻数k=18。

以故障切除后第1 个周期至第3 个周期的数据集为例进行实验分析，mDLM 与各基分类器以及浅层学习方法的测试结果如表2 所示。为了避免评估结果的偶然性和随机性，各项指标均为10 次抽样的平均值。

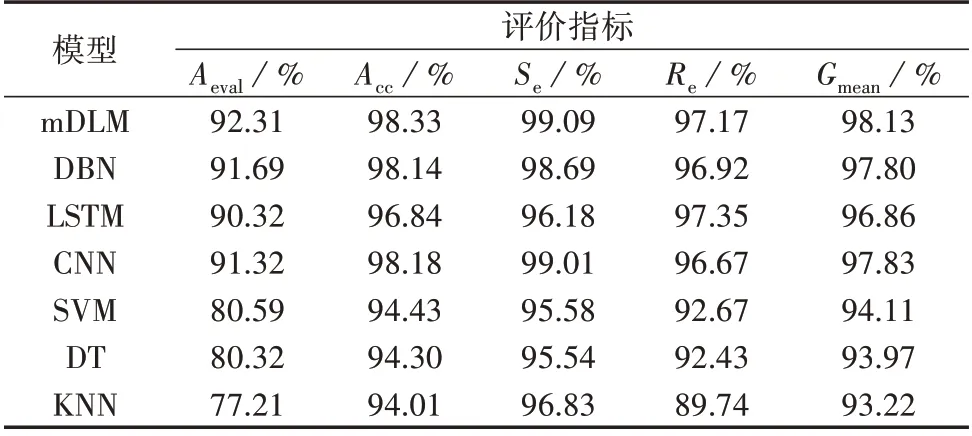
表2 不同模型的测试结果Table 2 Test results of different models

由表2 可知：相较于SVM、DT、KNN，mDLM 的评估准确率Aeval分别高11.72%、11.99%、15.10%，判稳准确率Acc分别高3.90%、4.03%、4.32%，这说明mDLM 凭借各类深度学习模型强大的特征提取和数据挖掘能力，能够有效地拟合电力系统输入特征和暂态稳定输出结果之间的非线性映射关系，从而获得比浅层学习更加优越的评估性能；相较于基分类器DBN、LSTM、CNN，mDLM 的评估准确率Aeval分别高0.62%、1.99%、0.99%，判稳准确率Acc分别高0.19%、1.49%、0.15%，这说明mDLM 能够取长补短，其评估性能要优于任意一个基分类器。

为进一步说明融合模型的有效性，从测试集中随机选取2 个故障场景，利用mDLM 和各基分类器预测故障场景属于不同类别的概率，见附录B 表B2和表B3。可以发现，即使个别样本被子分类器错分，通过模型融合也可使结果得以校正，从而在较短的响应时间内获得相对稳定的评估结果，这说明了对TSA问题进行多类型深度学习模型融合的必要性。

3.3 最佳迁移方案的选择

为了选择一种合适有效的迁移方案，以应对预训练集以外系统运行方式或拓扑结构的变化，以基分类器DBN 为例，将在基准负荷下训练的模型作为源域模型，并将其迁移至基准负荷的120%下。将目标域样本集按1∶3 的比例划分为训练集和测试集，将训练集作为连接源域和目标域的桥梁，用于迁移学习的训练和微调。迁移前以及采用3 种方案后模型的性能如图2所示。

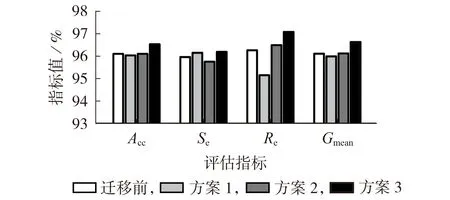
图2 不同迁移方案性能对比Fig.2 Performance comparison among different transfer schemes

由图2 可知：采用方案1 重新训练后，除了安全性指标Se优于迁移前外，其余各项指标均比迁移前的要低，这说明当目标域的训练样本数较少时，模型不能充分进行深层次的学习和训练，难以达到理想的效果；采用方案2 微调分类层的参数后，由于不能给目标域样本留出充足的学习空间，因此综合指标和迁移前的相当；采用方案3 微调整个网络后的效果最好，目标域网络有充足的学习空间，有利于适应目标域样本的特征表示，此外，共享原模型的结构和参数也为目标域提供了良好的学习起点。因此，在下文的分析中，迁移方案均选择方案3。值得说明的是，针对不同的迁移问题，最佳迁移方案往往不同，实际中应该根据具体的应用场景和分类任务选择合适的迁移方案。

3.4 超负荷水平下的迁移效果验证

3.4.1 迁移效果分析

为生成与初始训练集分布差异较大且不在模型泛化能力范围内的新样本，以验证迁移学习的有效性，将系统负荷水平分别调整至基准负荷的135%、140%、145%、150%，并相应调节发电机的出力，使得潮流计算收敛。故障设置与3.1节相同，仿真共生成14 960 个样本，包括3 183 个稳定样本和11 777 个失稳样本。将超负荷样本集按1∶1 的比例划分为训练集和测试集。3.2 节训练好的源域mDLM 在超负荷水平样本集上的测试结果如表3所示。

表3 超负荷水平的测试结果Table 3 Test results of overload level

由表3 可知，原mDLM 在超负荷水平下的评估性能下降较多，尤其是评估准确率Aeval和对失稳样本的识别率Re分别低于65%和90%，评估性能大幅下降，模型无法进行在线应用，因此需在该超负荷场景下对模型进行迁移更新。采用方案3，每次筛选的样本数Nm=187，分别从训练样本集中选择187、374、561、…、7 480 个样本对原模型进行迁移。迁移更新后的mDLM 以tmDLM 表示，迁移后的各基分类器分别表示为tDBN、tCNN、tLSTM，更新后的评估准确率Aeval和判稳准确率Acc分别如图3（a）、（b）所示。

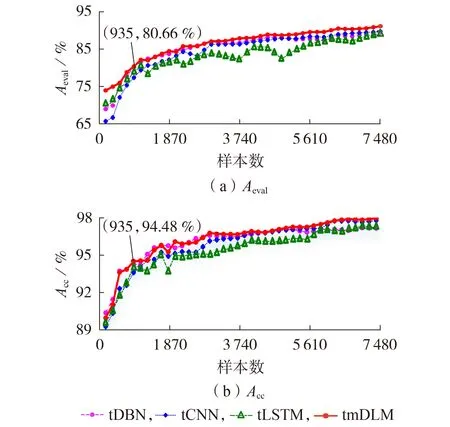
图3 超负荷水平下的迁移效果Fig.3 Transfer effect at overload level

由图3 可知，所选择的迁移样本数越多，迁移效果越好，模型在迁移初期性能恢复越快。本文所提融合tmDLM 方法的迁移效果优于任意一个基分类器。当用于迁移的样本数Dm=935 时，评估准确率Aeval从初始的62.67%恢复至80.66%，判稳准确率Acc从初始的90.07%恢复至94.48%，这说明融合tmDLM 方法仅利用较少的目标域样本集对源域模型进行迁移更新，即可快速得到适用于系统当前运行工况的模型，从而验证了该方法的有效性。

为分析所提方法在迁移更新过程中所需样本数的优势，将其和基分类器tDBN、tCNN、tLSTM 进行对比。当评估准确率Aeval恢复到85%时，tmDLM 和各基分类器的判稳准确率Acc均恢复到95%以上，此时融合模型所需的样本数为1 870，而基分类器tDBN、tCNN、tLSTM 在达到相同精度时所需的样本数分别为2 244、2 992、4 114，因此本文所提方法相比单一的深度迁移学习算法，在训练到相同精度时所需的样本数更少，缩短了样本生成和迁移更新的时间，有利于进行在线连续的暂态稳定自适应评估。

3.4.2 快速性分析

由于暂态稳定预测对快速性要求较高，为了分析融合tmDLM 方法的时效性，将tmDLM 与采用目标域样本集重新训练的效果进行对比。迁移与重新训练的效果对比如附录B 图B3 所示。由图B3（a）可知，当用于迁移的样本数相同时，tmDLM 的性能均优于重新训练，进一步说明了共享原模型的参数为新模型提供了较好的初值，使新模型具有良好的学习起点，而对参数微调能够使模型跟踪系统当前的运行方式。当评估准确率Aeval恢复到85%以上时，判稳准确率Acc达到95%，tmDLM 所需的样本数为1 870，微调时间为17.64 s，而重新训练所需的样本数为2 992，训练时间为127.92 s，模型自适应更新的效率提高了7.25 倍。由此可见，采用迁移的方式可以大幅提升模型更新训练的效率。经统计，在所有的测试样本集中，失稳样本的平均失稳时间为1.275 s，而所提方法评估一个样本的稳定／失稳程度等级仅需0.015 ms，本文样本集的响应时间为第1个周期至第3 个周期（共0.05 s），因此在样本发生失稳之前平均可以给调度人员留出1.225 s 的时间来采取紧急控制。此外，本文所提方法中各基分类器是并行训练的，不会增加时间复杂度。由此可见，本文所提方法可以满足在线TSA的快速性要求。

3.5 网架拓扑结构变化时的迁移效果分析

为了进一步验证本文所提融合tmDLM 方法的有效性，根据文献［15］新增如下4 种运行场景，用于模拟实际电力系统中发生大的连锁故障时，因多台发电机组和多条线路投退而引起的系统网架拓扑结构大的变化，并测试迁移更新后模型的评估性能。

场景A：负荷水平为基准负荷的50%，退出1 台发电机和4 条线路，共生成6 900 个样本，随机划分3 900个样本构成训练集，剩余样本构成测试集D1。

场景B：负荷水平为基准负荷的50%，退出5 台发电机和8 条线路，共生成6 900 个样本，随机划分3 900个样本构成训练集，剩余样本构成测试集D2。

场景C：负荷水平为基准负荷的150%，增加2台发电机和4 条线路，共生成3 960 个样本，随机划分2 960个样本构成训练集，剩余样本构成测试集D3。

场景D：负荷水平为基准负荷的150%，增加5台发电机和10 条线路，共生成8 580 个样本，随机划分4580个样本构成训练集，剩余样本构成测试集D4。

附录B 表B4 展示了新的运行场景下原融合模型的测试结果和迁移更新后的效果，各场景中迁移样本数Dm=561，学习率为0.001。由表可知，当系统运行方式或拓扑结构发生较大变化时，原来预训练好的模型性能骤降，尤其是在场景C 和场景D 下模型性能下降较多，而通过融合多类型的深度迁移学习在仅采用561 个目标域样本时，就可使模型快速恢复到原来的评估水平。

为了突出tmDLM 的效果，将其和文献［15］的CNN 进行对比。在场景C 和场景D 下，利用tmDLM得到的判稳准确率Acc均优于采用同样迁移方案下的CNN，CNN 采用的是故障切除后第1 个周期至第15 个周期的数据，可见，tmDLM 在分类难度大、响应时间短的情况下仍有较高的判稳准确率。

在场景D 下，通过融合迁移后，评估准确率Aeval比原模型提升了34.1%，判稳准确率Acc比原模型提升了8.6%且比CNN 迁移后的高3.3%，Gmean值比原模型提升了9.85%。因此tmDLM 能够有效地提高预测精度和更新效率，并且能够自适应地追踪系统的运行方式或拓扑结构的变化，从而实现离线训练和在线评估的精准匹配。

3.6 华中电网测试结果

为了进一步说明融合的必要性以及验证本文方法在更大规模系统中的适用性，采用华中电网的数据进行测试。华中电网全网共有690 台发电机、8492 条母线、4 474 条交流线路、13 条直流线路以及6 022 台变压器。暂态稳定计算程序选择中国电力科学研究院开发的电力系统分析综合程序（power system analysis software package，PSASP）。以5%为步长，设置基准负荷的75%～120%范围内的10种负荷水平，发电机出力随负荷变化而相应调整。随机选取4条线路，以10%为步长，设置输电线路全长的10%～90%范围内的9种故障位置，故障类型包括单相短路故障、两相短路故障以及三相短路故障，仿真时间为5 s。共生成14 040 个样本，包括10 446 个稳定样本和3594个失稳样本，按式（7）—（9）计算相应的稳定裕度和失稳程度指标，划分稳定裕度和失稳程度等级并贴上对应的标签。将样本按照2∶1的比例随机划分为训练集和测试集，响应时间仍为故障后的第1个周期至第3个周期。

将3.2节训练的新英格兰10机39节点系统作为源域模型，将其预训练好的各基分类器结构和参数作为华中电网评估模型的初始值。在此基础上采用方案3，每次筛选目标域的样本数Nm=374，迭代5次后模型性能基本恢复到原来的评估水平。由于目标域华中电网稳定样本数较多，样本不均衡更为明显，迁移过程中设置损失函数的权重值Ws=1、Wus=3。迁移前、重新训练、各基分类器迁移后的结果以及本文所提方法的测试结果如附录B表B5所示。

由表B5知：由于目标域华中电网与源域新英格兰10 机39 节点系统差异较大，将源域训练模型直接应用于目标域时性能表现较差；原始模型在华中电网的评估准确率仅为60.04%，判稳准确率仅为84.87%，而采用本文所提方法在源域预训练模型的基础上进行微调，仅需13.28 s 就可将评估准确率恢复到96.89%，将判稳准确率恢复到98.99%。将本文所提方法与重新训练的结果进行对比可知，本文所提方法的各项评估指标均优于重新训练，重新训练的样本数为9 360，训练时间为421.08 s，本文所提方法的模型训练更新效率比重新训练提高了31.7倍，这说明本文所提方法不仅可自适应跟踪系统运行方式或拓扑结构的变化，而且在结构和规模完全不同的系统之间进行迁移也是有效的。将tDBN、tCNN、tLSTM 以及本文所提方法的结果进行对比可知，本文所提方法的评估准确率、判稳准确率、Gmean比基分类器中表现最好的分别高0.44%，0.51%、0.23%，由于各基分类器是同时并行训练的，不会花费额外的时间，而融合机制的时间花费为ms 级，因此本文通过模型融合可在相同的时间内获得更好的评估性能。

4 结论

针对单一模型泛化能力不足以及电力系统运行工况发生较大变化时TSA 模型性能下降的问题，为了提高深度学习模型评估性能的稳定性和自适应能力，本文提出一种融合tmDLM 的评估方法，在新英格兰10 机39 节点系统以及华中电网上进行仿真验证，得到如下结论。

1）融合不同类型深度学习模型可以充分发挥各类模型的优势，从而提高TSA 输出结果的稳定性。所提融合模型在判稳的同时进行稳定裕度／失稳程度等级的评估，输出信息多样化，有效缩短了模型的预测和评估时间。

2）融合tmDLM 可以有效跟踪系统的运行方式或拓扑结构的变化，且可以在结构和规模完全不同的系统之间进行迁移。通过模型的迁移和有限的微调，模型在目标域的评估精度和更新速度都得到大幅提高，实现了电力系统暂态稳定的自适应评估。

对调度人员无法预知的紧急变化情况，针对新的拓扑结构快速生成最少量且最富有信息的样本并对模型进行在线迁移更新，以及进一步考虑增加融合的学习方法对整体评估效果的影响，将是下一步研究工作的重点。

附录见本刊网络版（http：//www.epae.cn）。