一种永磁同步电机可视化双矢量调制模型预测控制方法

郭磊磊，王朋帅，李琰琰，陈亚斐，金 楠

（郑州轻工业大学电气信息工程学院，河南郑州 450002）

0 引言

近年来，永磁同步电机因其具有效率高、功率密度大等优点而在新能源汽车、飞轮储能、风力发电等领域得到广泛应用［1-3］。为了实现永磁同步电机的高性能控制，矢量控制和直接转矩控制得到广泛研究和应用［4-5］。然而，矢量控制需要复杂的脉宽调制（pulse width modulation，PWM）模块，而直接转矩控制则存在转矩脉动较大等问题。为了解决永磁同步电机常规控制策略所存在的缺点，近年来，各种新型控制策略得到广泛研究［6-7］。

2007年，智利圣玛利亚理工大学J. Rodriguez教授等在文献［8］中提出了一种两电平电压源逆变器模型预测控制策略。该方法具有无需设计PI 控制参数、无需设计PWM 模块即可实现逆变器快速控制的优点，因此其在PWM 整流器［9］、交流电机控制［10］等领域迅速得到广泛研究。然而，常规的模型预测控制策略由于每个控制周期仅使用1 个电压矢量，导致电流和转矩纹波较大。虽然提高采样频率可以减小预测控制的电流和转矩纹波，但采样时间受控制算法计算量的限制。

为了减小电流和转矩纹波，诸多学者在文献［8］的基础上提出并研究了双矢量及三矢量模型预测控制策略。与文献［8］不同，双矢量法在每个控制周期同时选择2 个电压矢量进行作用，从而可以提高电流和转矩控制精度，减小纹波［11］。三矢量法则在每个控制周期同时选择3 个电压矢量进行作用，从而可进一步减小电流和转矩纹波［12］。然而，虽然上述多矢量模型预测控制方法有助于改善永磁同步电机的动稳态控制性能，但也存在计算量大等问题。

为了实现多矢量模型预测控制并降低计算量，文献［13-14］提出并研究了一种调制模型预测控制策略。与文献［11-12］不同，文献［13-14］所提方法在计算电压矢量作用时间时，假设每个电压矢量的作用时间与其目标函数值成反比，电压矢量作用时间计算方法具有实现简单、计算量小、不会出现矢量作用时间小于0 或大于控制周期的问题等优点，因此在矩阵变换器［15］、有源电力滤波器［16］控制等领域得到广泛研究。然而，虽然诸多学者研究了调制模型预测控制策略，并通过仿真和实验验证了其有效性，但直接假设电压矢量作用时间与其目标函数值成反比仍缺乏严格的理论基础，这阻碍了这类方法的推广应用。

为了解决这一问题，文献［17］提出了基于电压矢量几何关系的分析方法，初步证明了多矢量调制模型预测控制的有效性，但该方法只能证明当目标函数为电流误差的平方和的开方形式时多矢量调制模型预测控制的有效性。一旦目标函数采用电流误差绝对值之和或电流误差平方和的形式时，由于电压矢量和目标函数的关系变得很复杂，文献［17］所提基于几何关系的分析方法将不再适用。

因此，本文提出了一种新的可视化分析方法，并将其分别用于分析不同目标函数下的双矢量调制模型预测控制，从而进一步证明了双矢量调制模型预测控制的有效性。与文献［17］相比，本文所提方法是一种基于代数关系的分析方法，不受几何关系的限制，因此这是一种更广义的分析方法。此外，本文所提可视化分析方法还可以扩展到三矢量模型预测控制中。详细的实验结果验证了多矢量调制模型预测控制的有效性以及所提可视化理论分析的正确性。

1 常规单矢量模型预测控制方法

本文以两电平电压源逆变器驱动永磁同步电机为研究对象，其拓扑结构如图1（a）所示。图中：udc为直流侧母线电压；O为电压中性点；S1—S6为逆变器6个开关管；ia、ib、ic为三相电流。两电平逆变器共能产生8 个电压矢量，包括2 个零矢量（u0（000）和u7（111））、3 个奇矢量（u1（100）、u3（010）、u5（001））和3 个偶矢量（u2（110）、u4（011）、u6（101）），如图1（b）所示。

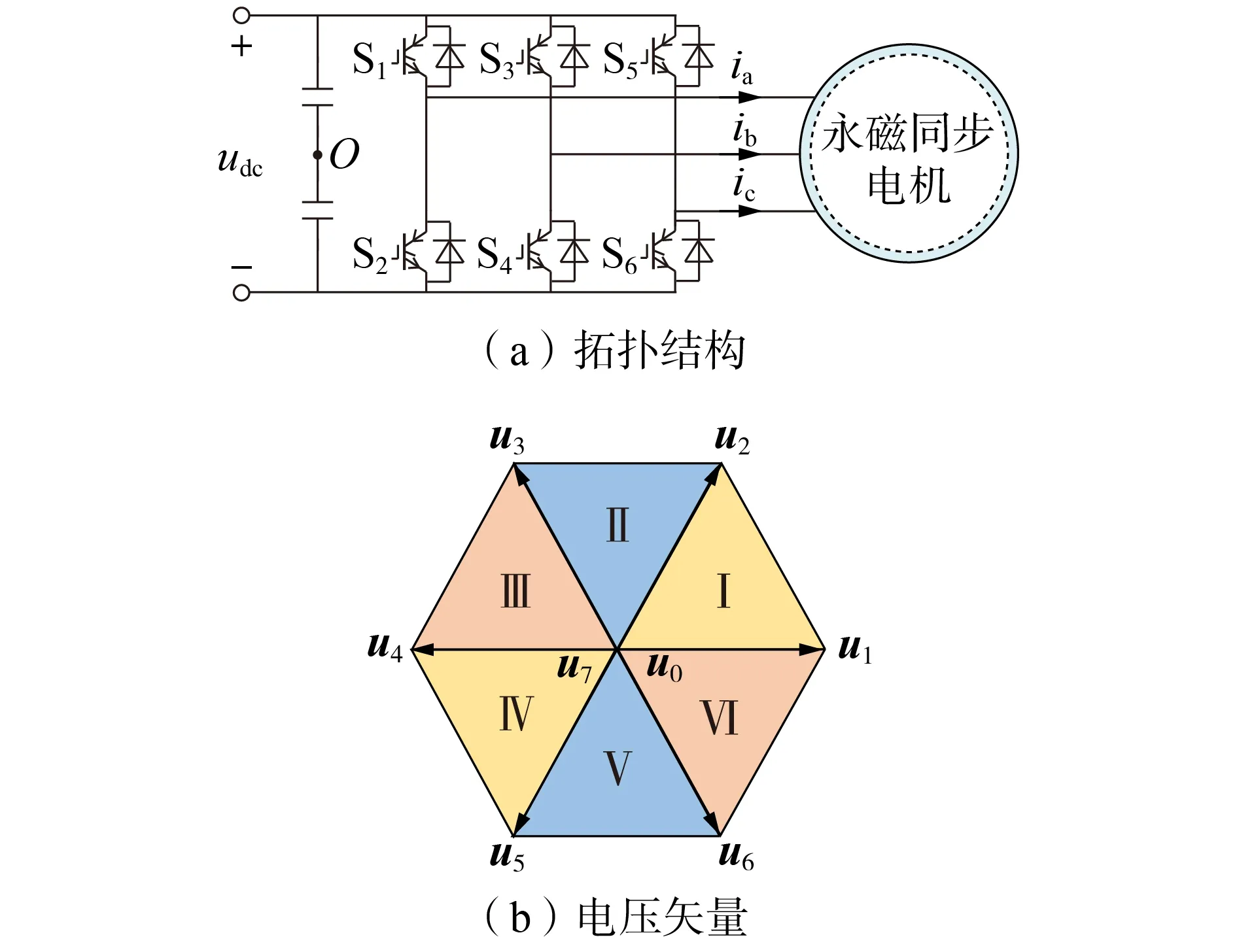
图1 系统的拓扑结构和电压矢量Fig.1 Topology structure and voltage vectors of system

在α β静止坐标系下，永磁同步电机的数学模型可表示为：

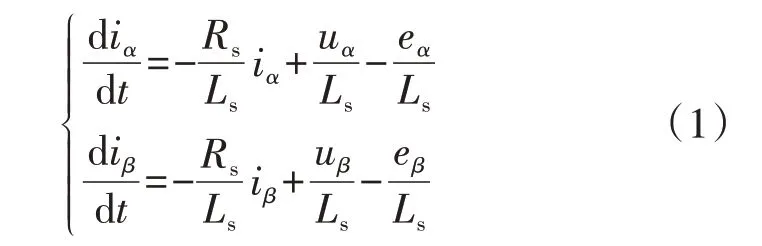
式中：iα、iβ为永磁同步电机的定子电流；uα、uβ为永磁同步电机的定子电压，即逆变器的输出电压；Rs为定子电阻；Ls为定子电感；eα、eβ为永磁同步电机的等效反电动势，且满足式（2）所示关系。

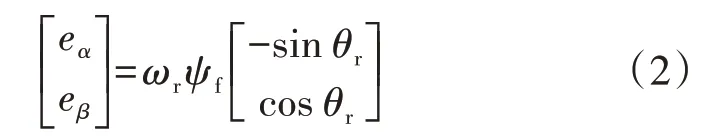
式中：θr为永磁同步电机的转子角度；ωr为同步转速；ψf为永磁体磁链。

对式（1）进行离散化，可得：

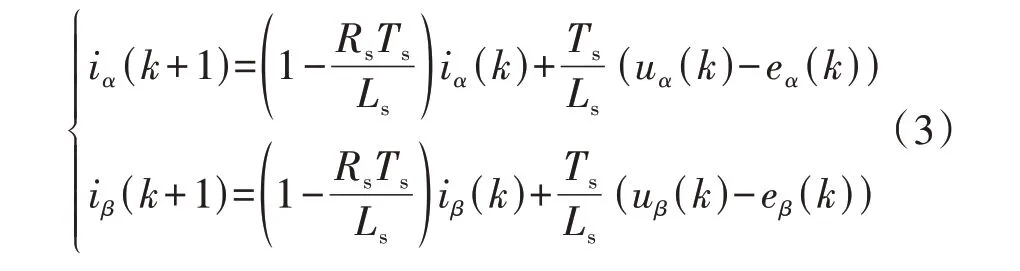
式中：x(k)、x(k+1)分别表示变量x在k、k+1 时刻的值，x代表iα、iβ、uα、uβ、eα、eβ；Ts为控制周期。

为了补偿模型预测控制的固有延时，可将上一个周期选择的最优电压矢量u=［uα uβ］T代入式（3）预测k+1 时刻的电流iα(k+1)、iβ(k+1)，然后将逆变器的8 个电压矢量和电流iα(k+1)、iβ(k+1)代入式（4）预测k+2时刻的电流iα(k+2)、iβ(k+2)，进而将预测值代入式（5）所示的目标函数g中进行最优电压矢量选择，并将使目标函数最小的电压矢量作用于永磁同步电机。

由于常规永磁同步电机模型预测控制策略的每个控制周期仅使用1 个电压矢量，导致其电流和转矩纹波较大。针对该问题，文献［13］提出了永磁同步电机双矢量调制模型预测控制方法，但该方法缺乏严格的理论证明，导致其推广应用受到阻碍。因此，本文提出了一种可视化分析方法，从理论上验证其有效性。

2 双矢量调制模型预测控制

2.1 虚拟矢量合成

为了便于对比与常规单矢量模型预测控制的区别，本文所述双矢量调制模型预测控制的目标函数同样定义为电流误差的绝对值之和，如式（6）所示。

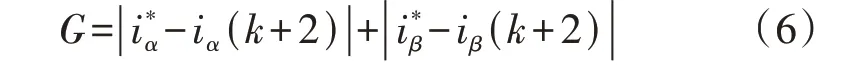
如图1（b）所示，由于两电平逆变器的8 个基本电压矢量的幅值和相位固定，因此，每个周期仅有1个电压矢量作用时，其控制精度较低。

为了提高控制精度，降低电流和转矩谐波，本文将相邻电压矢量进行两两组合，构成了12 组双矢量组合，由此可以合成12个虚拟矢量，包括6个虚拟奇矢量（uv1（u0，u1）、uv3（u0，u2）、uv5（u0，u3）、uv7（u0，u4）、uv9（u0，u5）、uv11（u0，u6））和6 个虚拟偶矢量（uv2（u1，u2）、uv4（u2，u3）、uv6（u3，u4）、uv8（u4，u5）、uv10（u5，u6）、uv12（u6，u1）），如图2所示。图中每个虚拟矢量与基本矢量之间的组合关系满足式（7）。

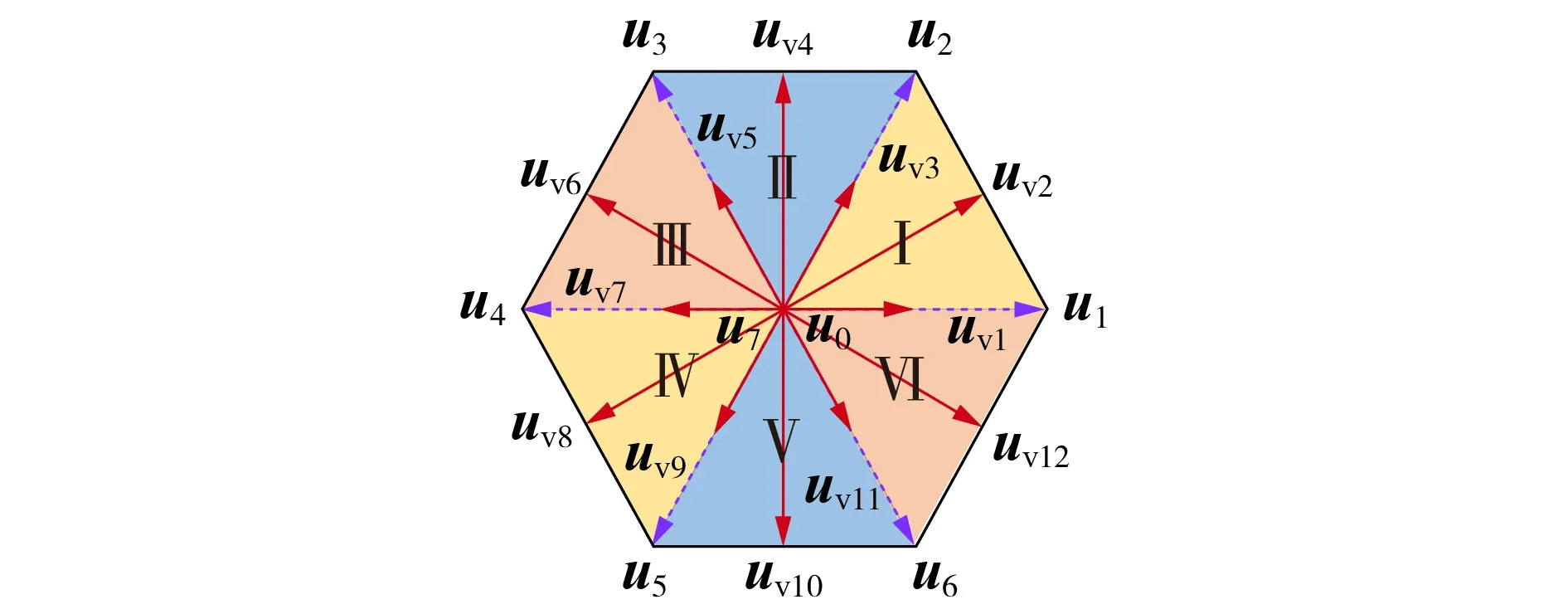
图2 电压矢量组合Fig.2 Combinations of voltage vectors

式中：uvi（i=1，2，…，12）为合成的虚拟矢量；uj（j=0，1，…，6）、uk（k=0，1，…，6）为逆变器的基本电压矢量；ti，uj和ti，uk分别为uj和uk的作用时间，且满足式（8）所示关系。

由图2 可知：当采用零矢量和非零矢量组合时，组合后的虚拟矢量幅值可调；当采用2个非零矢量组合时，组合后的虚拟矢量相位可调。因此，当每个控制周期同时采用2 个电压矢量时，由于电压矢量自由度的增加，转矩和电流控制精度均可以得到提高。

根据调制模型预测控制原理，为了合理计算式（7）中每个电压矢量的作用时间，可假设矢量作用时间与其目标函数值成反比［13-14］，即满足：

式中：m为一个正的比例系数；ts（s=0，1，…，6）为每个基本电压矢量的作用时间；Gs（s=0，1，…，6）为每个基本电压矢量所对应的目标函数。

结合式（8）和式（9）即可计算出合成每个虚拟电压矢量时，2 个基本电压矢量所对应的作用时间。以虚拟矢量uv1为例，uv1由u0和u1合成，而u0和u1的作用时间可根据式（8）和式（9）计算得到，满足：

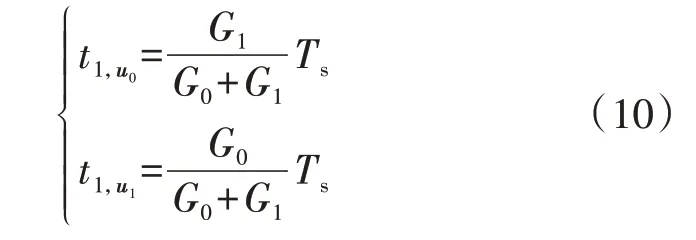
2.2 电压矢量预选与优化

由于每个控制周期需要同时对合成的12 个虚拟矢量进行在线优化，这大幅增加了计算量。为了简化算法，本文采用了一种改进的矢量预选策略，可将每个周期需要优化的电压矢量数量由12 个减少为3个。

首先，本文将图2 所示的电压矢量平面平均分为6个扇区（扇区Ⅰ—Ⅵ），每个扇区由相邻的2个非零矢量和1 个零矢量组成；其次，令t2N，uN、t2N，uN+1（N=1，2，…，6）均为Ts/2，此时6 个虚拟偶矢量uv2N为6 个扇区的中间矢量，将这6 个虚拟矢量依次代入式（4）和式（6），并通过目标函数比较优化，可得到最优虚拟电压矢量；然后，可根据最优虚拟电压矢量所在扇区选择需要在线优化的3 个虚拟矢量，如附录A 表A1所示；在确定了3个备选虚拟矢量后，需要根据式（8）和式（9）计算电压矢量作用时间，进而确定3 个备选虚拟矢量的大小，再将这3 个备选虚拟矢量代入式（5）进行目标函数优化，并选择使目标函数最小的电压矢量作为最优矢量，在下一周期用于控制永磁同步电机。为了清晰起见，附录A 图A1给出了本文所述方法的控制流程图。

2.3 可视化理论分析

由于双矢量模型预测控制所使用的12 个虚拟电压矢量是可调的，在电压矢量图形上可以理解为其幅值与相位是可调节的，因此可以通过适当地使用虚拟电压矢量来降低控制误差。虽然文献［13-14］在假设每个电压矢量的持续时间与其目标函数值成反比的情况下研究了模型预测控制策略，但仍然缺乏严格的理论依据。为此，本文提出了一种可视化分析方法，对比分析双矢量模型预测控制的控制误差，为双矢量模型预测控制的有效性提供理论依据。

首先，根据式（1）和无差拍理论可知［18］，当下一周期实际电流跟踪参考值时，参考电压满足：

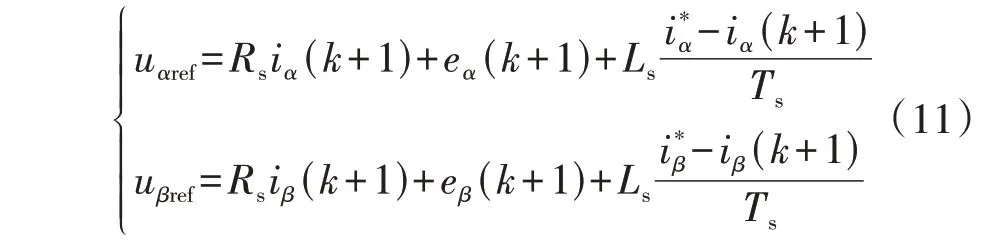
式中：uαref、uβref为参考电压。

联立式（4）、式（6）和式（11）可得：

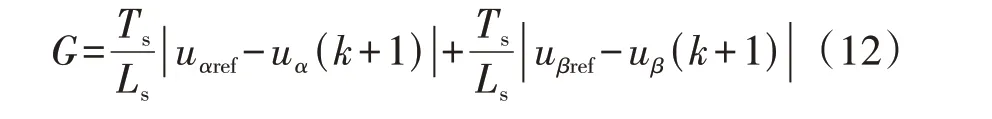
由此可见，式（6）所示电流误差目标函数可以等价转化为电压误差目标函数。

其次，将式（12）作为新的目标函数对双矢量模型预测控制的有效性进行分析。以参考电压矢量位于扇区Ⅰ为例，定义Gmui为基本电压矢量ui作用时所对应的电压误差目标函数。附录A图A2为扇区Ⅰ常规单矢量模型预测控制电压误差目标函数几何分析图。由图可知，当参考电压矢量位于扇区Ⅰ任意位置时，基本电压矢量u0、u1、u2所对应的目标函数为：

式中：uαi、uβi（i=1，2）分别为ui的α、β轴分量。

同理，定义Gnuvi为虚拟矢量uvi作用时所对应的电压误差目标函数，其几何分析如附录A 图A3 所示。利用基本电压矢量u0、u1、u2所对应的电压误差目标函数，并结合式（7）—（9）可计算出虚拟矢量uv1、uv2、uv3与基本电压矢量关系表达式为：

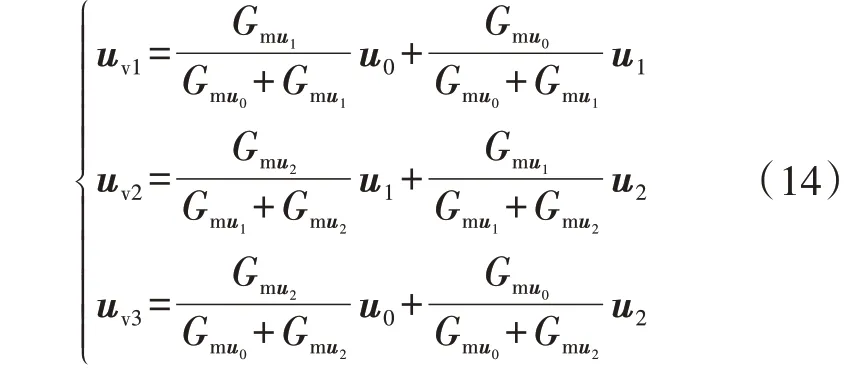
因此由图A3可知，当参考电压矢量位于扇区Ⅰ任意位置时，虚拟矢量uv1、uv2、uv3所对应的目标函数为：

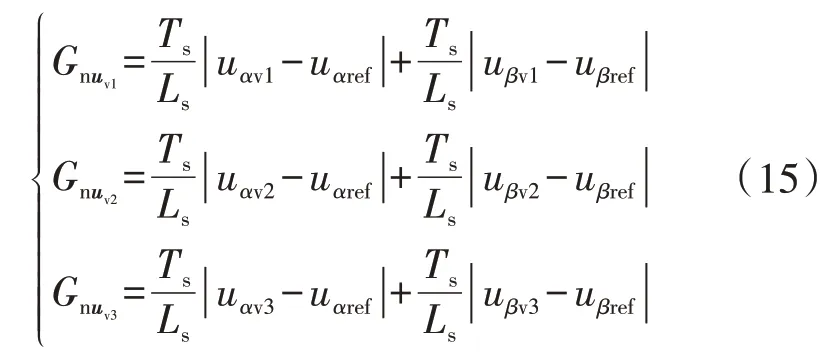
式中：uαvi、uβvi（i=1，2，3）分别为uvi的α、β轴分量。

然后，定义g1、g2分别为单矢量模型预测控制和双矢量调制模型预测控制在扇区Ⅰ内选取的最小目标函数，如式（16）所示。为了表明本文所述双矢量调制模型预测控制方法的有效性，本文将扇区Ⅰ内双矢量调制模型预测控制与单矢量模型预测控制的最小目标函数进行对比分析，当证明双矢量调制模型预测控制最小目标函数更小，即g2＜g1时，代表其控制误差更小，其控制效果也更优。

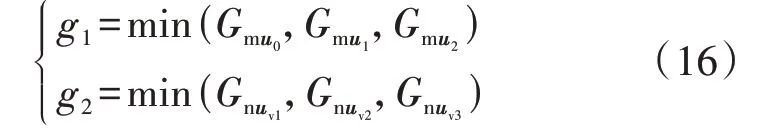
最后，以参考电压uref位于扇区Ⅰ内任意位置情况下，基于2 种控制的最小目标函数画出关于误差J=g2-g1的可视化三维图，可视图以扇区Ⅰ所在区域作为零平面，以误差J作为纵轴进行结果分析，如图3 所示。由图可知，可视化三维图全部位于零平面下方，误差J≤0，即g2≤g1，其中当参考电压矢量位于扇区Ⅰ内3 个基本电压矢量u0、u1、u2位置时g2=g1。因此，在扇区Ⅰ内双矢量调制模型预测控制的误差更小、效果更优。

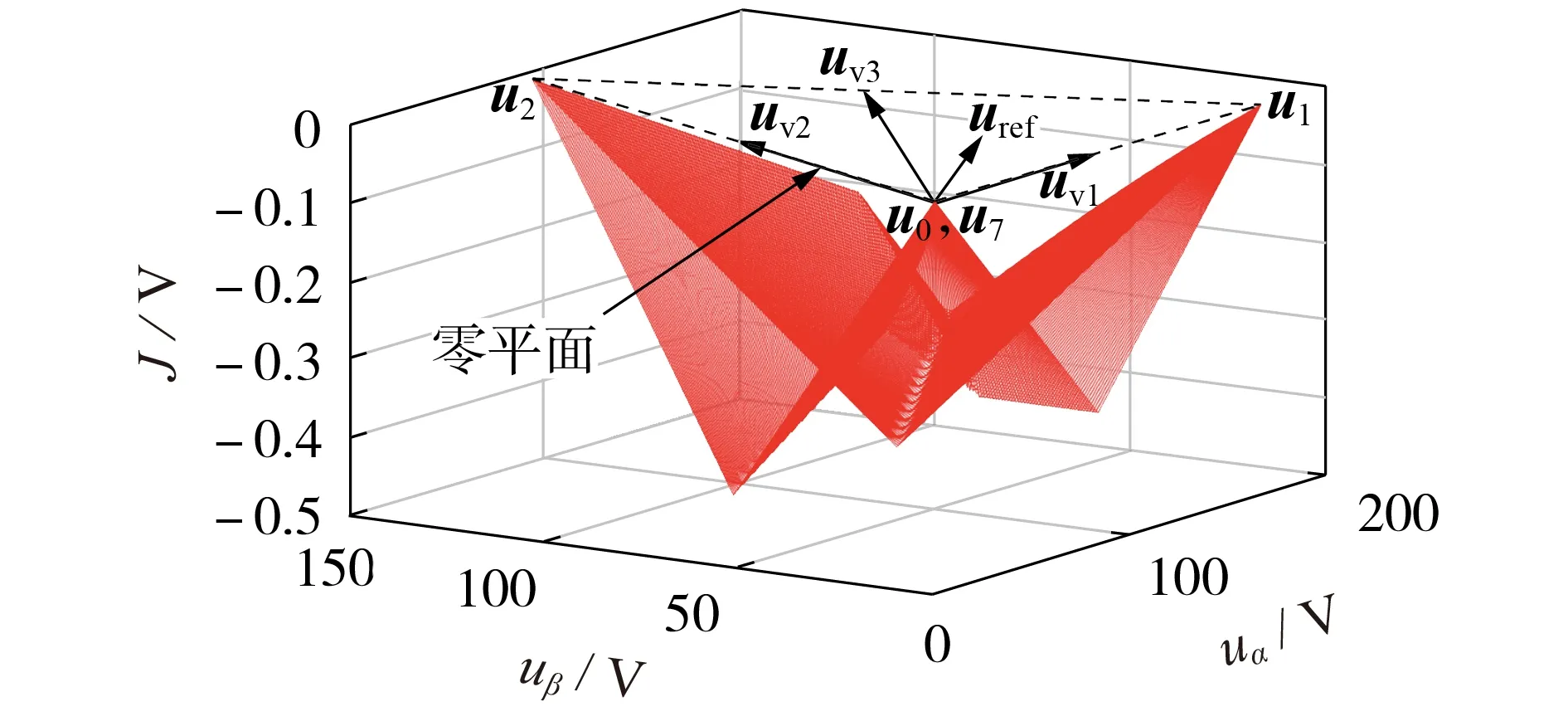
图3 所述方法有效性分析可视图（扇区Ⅰ）Fig.3 Visual diagram of effectiveness analysis of described method（Sector Ⅰ）

同理，可以得到扇区Ⅱ—Ⅵ内关于误差J的可视化三维图，如附录A 图A4 所示。由图可知，其他扇区可以得到与扇区Ⅰ相同的结论，即双矢量调制模型预测控制效果优于单矢量模型预测控制。

图4 为双矢量模型预测控制有效性分析可视化总图。由图可知，无论参考电压矢量位于哪个扇区，双矢量调制模型预测控制误差减去单矢量模型预测控制误差皆小于等于0，即J≤0，因此双矢量调制模型预测控制可以减小控制误差，降低电流谐波，改善电流质量。本文所提可视化分析结果验证了双矢量调制模型预测控制的有效性。

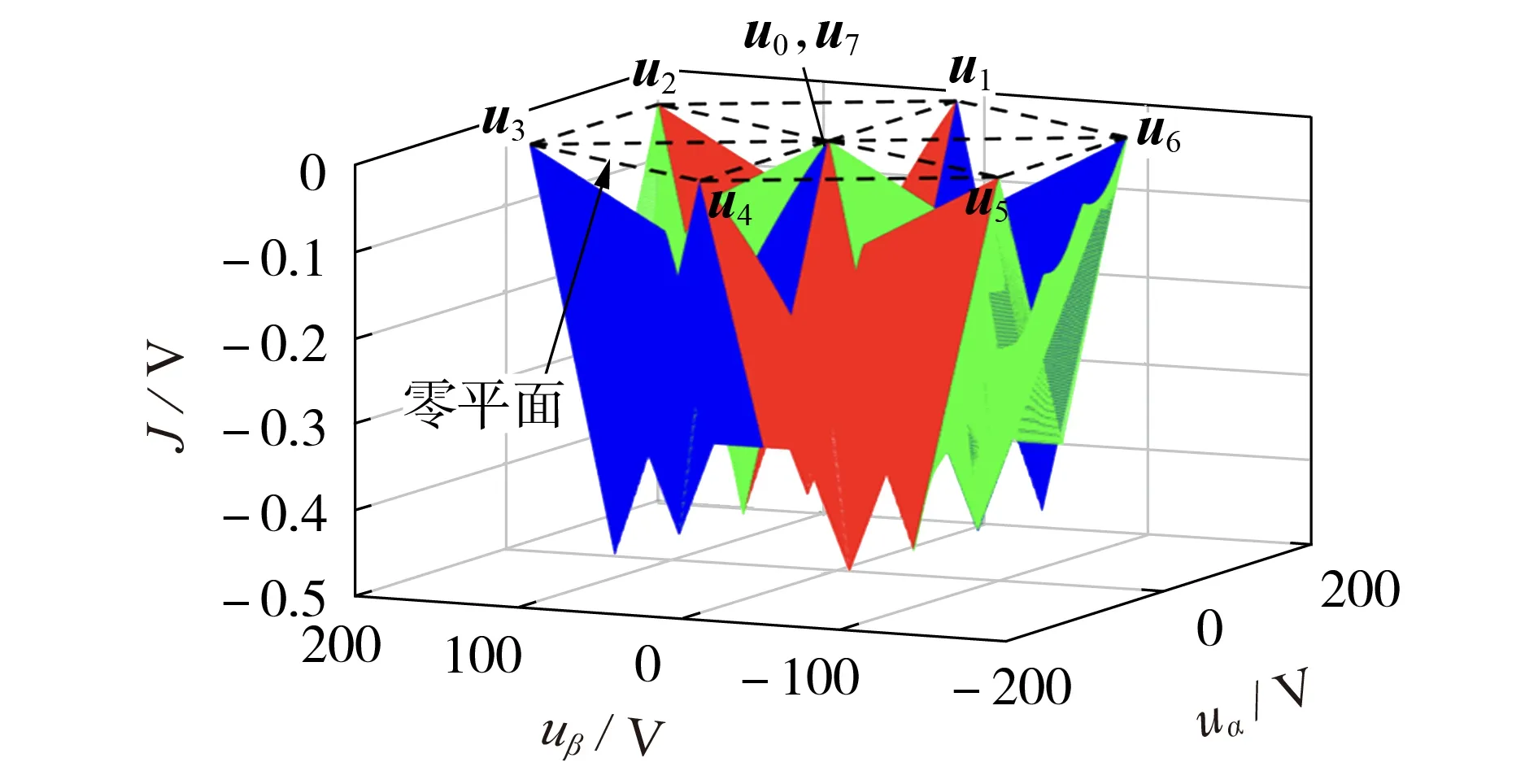
图4 所提方法有效性分析可视总图Fig.4 General visual diagram of effectiveness analysis of proposed method

上述理论分析建立在式（6）、式（12）所示绝对值之和目标函数基础上。为了进一步验证本文所提可视化分析方法的正确性，本文还对如式（17）所示的另一目标函数Gv下的双矢量调制模型预测控制进行了有效性分析，分析结果如图5所示。

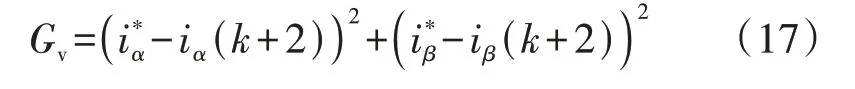
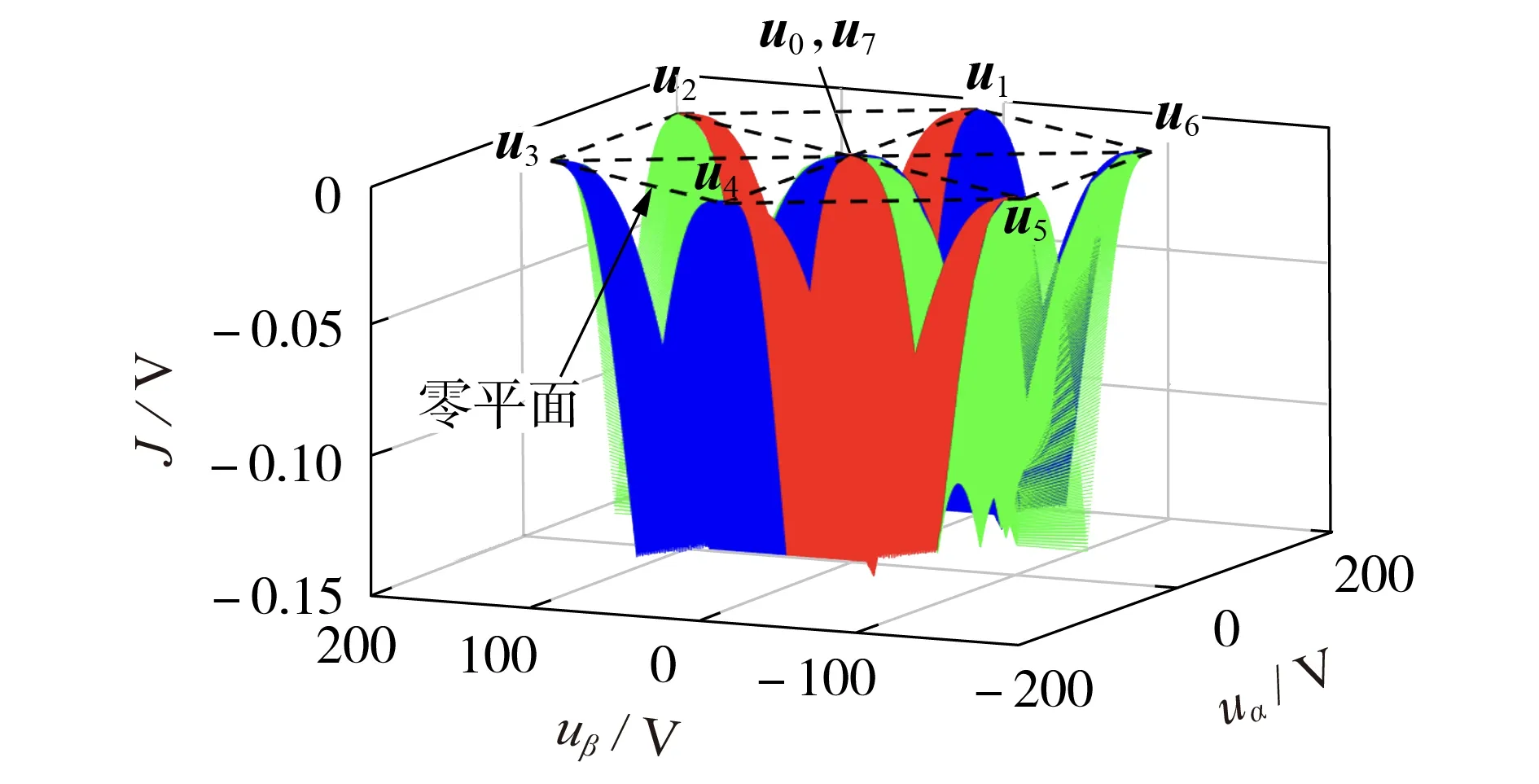
图5 式（17）下所提方法有效性分析可视总图Fig.5 General visual diagram of effectiveness analysis of proposed method under Equation（17）

由图5 可见，本文所提可视化分析方法不仅可为基于式（6）所示目标函数的双矢量调制模型预测控制的有效性提供理论依据，而且可以为基于式（17）所示目标函数双矢量调制模型预测控制的有效性提供理论依据，这证明了本文所提可视化分析方法的可推广性。

3 所提可视化分析方法的推广

为了进一步证明本文所提可视化分析方法的正确性和可推广性，将其扩展到三矢量调制模型预测控制中，通过可视化分析证明三矢量调制模型预测控制的有效性，从而为三矢量调制模型预测控制提供坚实的理论基础。

首先对基于式（6）所示目标函数的三矢量调制模型预测控制的有效性进行可视化分析。与双矢量调制模型预测控制不同，三矢量调制模型预测控制在每个控制周期采用3 个电压矢量作用来提高控制精度［19］。其方法是将1 个零矢量和2 个相邻的非零矢量进行组合，构成6组三矢量组合，由此可合成6个虚拟矢量，即uvv1（u0，u1，u2）、uvv2（u0，u2，u3）、uvv3（u0，u3，u4）、uvv4（u0，u4，u5）、uvv5（u0，u5，u6）和uvv6（u0，u6，u1），如附录A 图A5 所示，图中各虚拟矢量与基本矢量之间的组合关系如下：

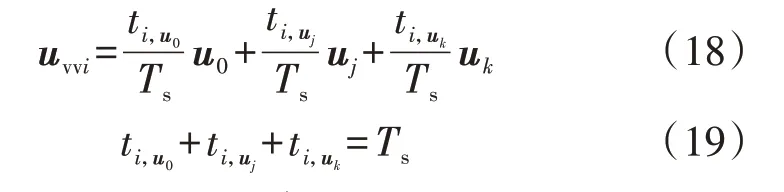
式中：uvvi（i=1，2，…，6）为合成的虚拟矢量；j，k=1，2，…，6。

根据调制模型预测控制原理，为了合理计算式（18）中每个电压矢量的作用时间，同样假设电压矢量作用时间与其目标函数值成反比，即满足式（9）所示关系。结合式（19）和式（9）即可计算出每个电压矢量的作用时间为：

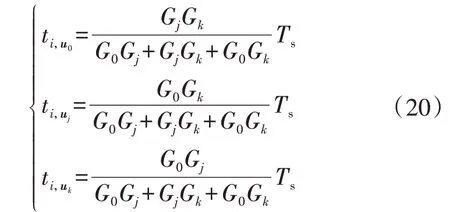
式中：Gj、Gk分别为基本电压矢量uj、uk对应的目标函数值。

采用上述同样的可视化分析方法对三矢量调制模型预测控制进行有效性分析，以6 个扇区作为零平面，以每个扇区内三矢量与单矢量最小目标函数的误差作为纵轴，可得如附录A 图A6（a）所示的可视化分析结果。由图可见，与单矢量模型预测控制相比，三矢量调制模型预测控制可以减小控制误差，从而为三矢量调制模型预测控制的有效性提供了坚实的理论基础。同理，采用同样的可视化分析方法可以得到基于式（16）所示目标函数的三矢量调制模型预测控制可视化分析结果，如附录A 图A6（b）所示。由图可见，采用本文所提可视化分析方法可进一步证明三矢量调制模型预测控制的有效性。这也进一步证明了本文所提可视化分析方法的可推广性。

4 实验验证

为了进一步验证本文所述多矢量调制模型预测控制的有效性以及所提可视化分析的正确性，本文建立了附录B 图B1 所示的实验平台，并与常规的单矢量模型预测控制进行了实验对比研究。实验所用电机参数如附录B表B1所示。

4.1 双矢量调制模型预测控制实验验证

为了验证本文所述双矢量调制模型预测控制的有效性，首先进行了电流环实验对比研究。实验时，电机运行转速设为750 r／min，转矩电流设为从5 A突增至15 A，励磁电流设为0。图6为单矢量模型预测控制和双矢量调制模型预测控制下电流环实验结果。对比图6（a）和图6（b）可知，与单矢量模型预测控制相比，双矢量调制模型预测控制可以大幅提高电流的控制精度，实现电流纹波抑制。实验结果验证了本文所提控制方法的有效性以及可视化分析的正确性。

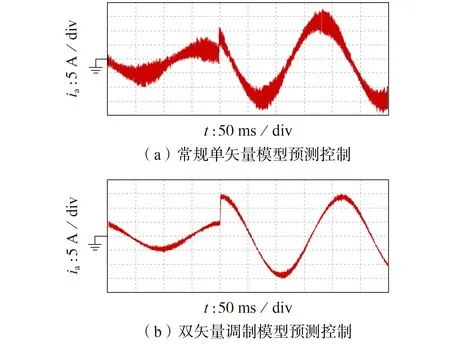
图6 电流环实验结果Fig.6 Experimental results of current loop

为了进一步验证所述双矢量调制模型预测控制的有效性，本文对转速闭环控制进行了实验对比研究。附录B图B2和图7对比研究了永磁同步电机参考转速ωref由150 r／min 突增为750 r／min 时单矢量模型预测控制和双矢量调制模型预测控制下转速动态响应性能。对比可知：2 种控制均具有较好的转速跟随性能；在动态过程中，双矢量调制模型预测控制策略的电流纹波更小。这验证了本文所述双矢量调制模型预测控制的有效性以及所提可视化分析的正确性。

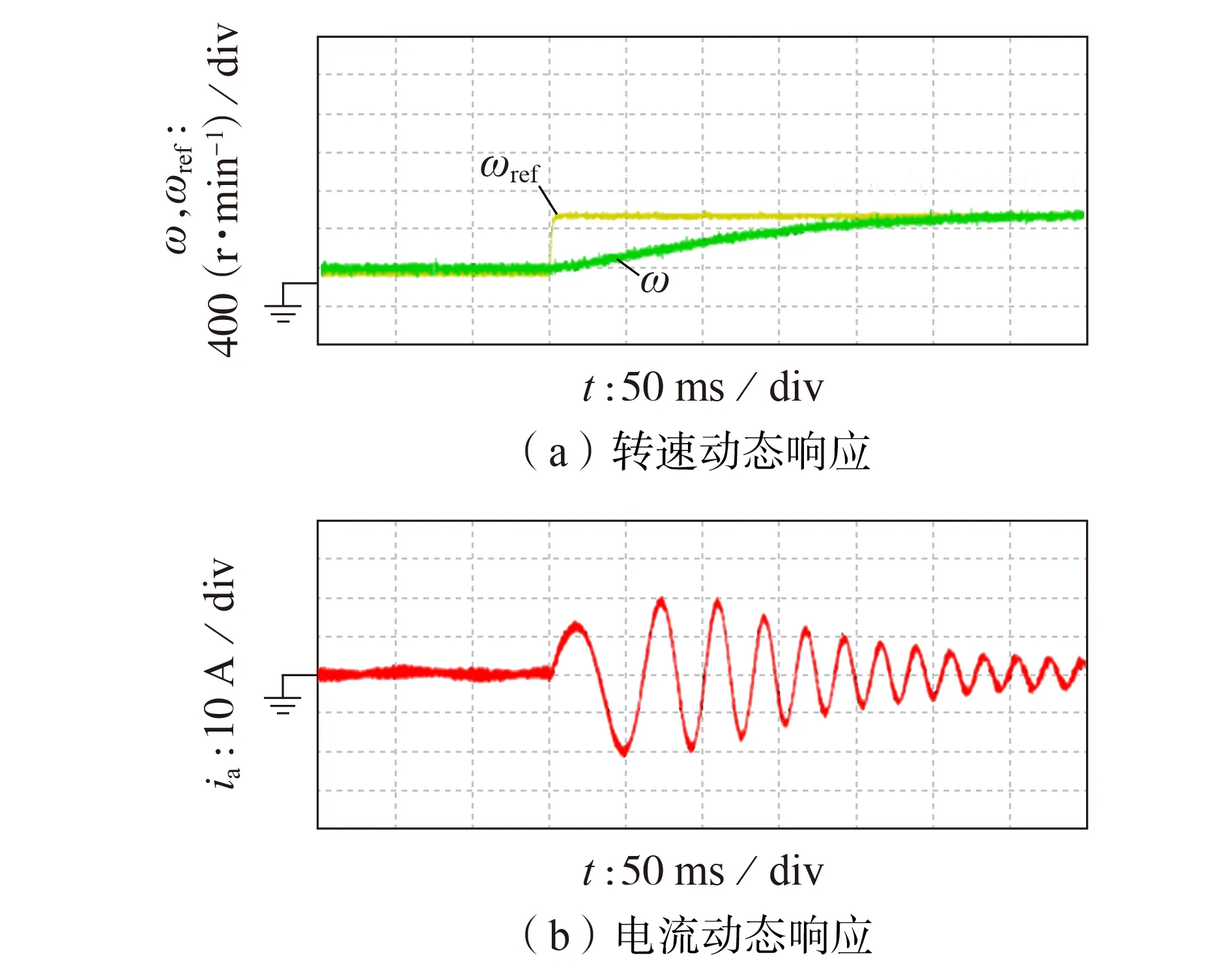
图7 双矢量调制模型预测控制下转速环实验结果（1）Fig.7 Experimental results of speed loop under dual-vector modulated model predictive control（1）

图8和附录B图B3进一步给出了电机参考转速ωref由-750 r／min 突增为750 r／min 时的正反转实验结果。对比可知：在电机正反转运行时，2 种控制均具有较好的转速动稳态特性；且双矢量调制模型预测控制的电流纹波更小。本文所提可视化分析方法揭示了双矢量调制模型预测控制的有效性，实验结果进一步验证了双矢量调制模型预测控制的有效性以及本文所提可视化分析的正确性。

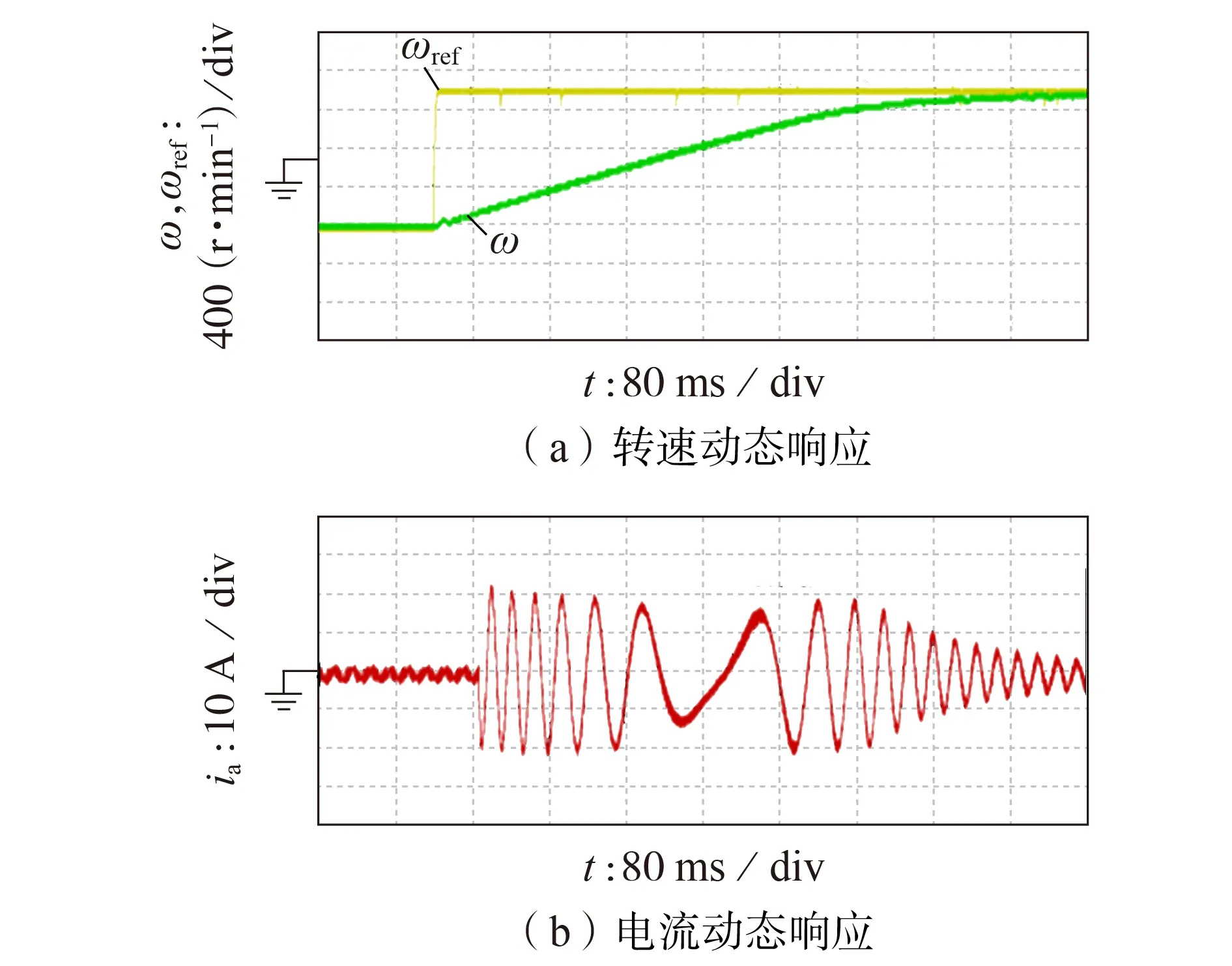
图8 双矢量调制模型预测控制下转速环实验结果（2）Fig.8 Experimental results of speed loop under dual-vector modulated model predictive control（2）

4.2 扩展

为了进一步验证本文所提可视化分析方法的有效性，将其推广应用于三矢量调制模型预测控制，并进行了实验验证。实验参数与附录B表B1相同。

图9（a）给出了转速为750 r／min 时，基于式（6）所示目标函数的三矢量调制模型预测控制下a 相电流实验波形。通过与上述常规单矢量对比可见，三矢量调制模型预测控制下电流纹波明显更小。这不仅验证了三矢量调制模型预测控制的有效性，而且进一步证明了本文所提可视化分析方法的正确性。

另外，文献［14，20］研究了一种将模型预测控制与空间矢量调制相结合的调制模型预测控制方法，该方法通过在模型预测控制算法中加入空间矢量调制技术来固定开关频率，进而提高模型预测控制的性能。为了对比研究该方法与三矢量调制模型预测控制的差别，图9（b）给出了文献［14，20］方法在相同开关频率下的a 相电流实验波形。对比图9（a）、（b）可见，两者电流波形及总谐波畸变率（total harmonic distortion，THD）相差不大，表明这2种方法具有类似的控制效果。

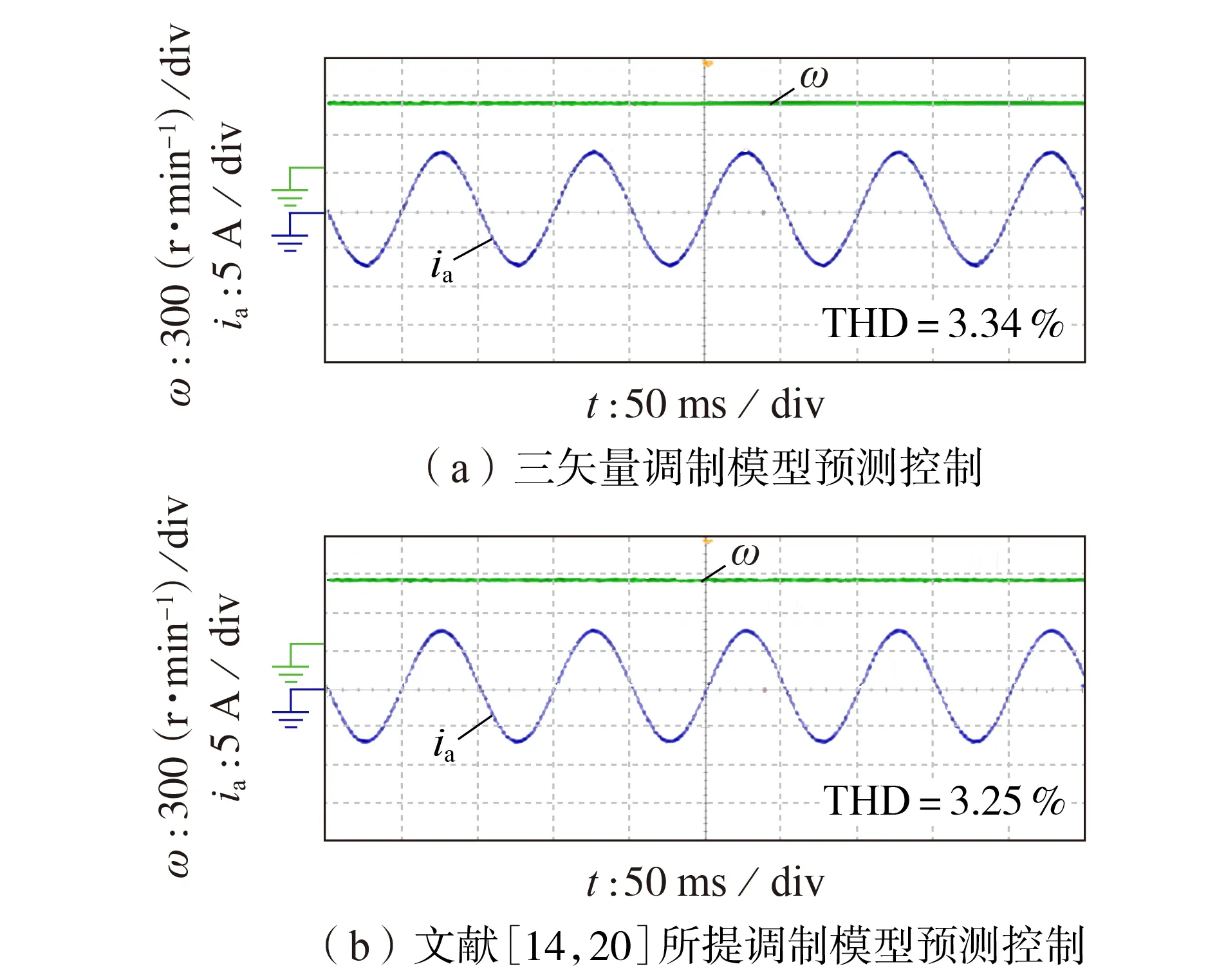
图9 转速环静态实验结果Fig.9 Static experimental results of speed loop

三矢量调制模型预测控制方法与文献［14，20］所提方法的主要区别在于：文献［14，20］所提方法结合了空间矢量调制可以实现恒开关频率控制，因此其电流谐波较小；三矢量调制模型预测控制通过每个周期采用3 个电压矢量作用，也可以实现恒开关频率控制，因此其电流谐波也较小。此外，三矢量调制模型预测控制方法通过修改目标函数，还可以进一步实现开关频率调节、共模电压抑制等多目标优化，这是多矢量调制模型预测控制的主要优点。

5 结论

为了实现永磁同步电机低电流谐波模型预测控制，本文采用了一种基于目标函数的双矢量调制模型预测控制方法。但该方法假设每个电压矢量的作用时间与其目标函数值成反比缺乏严格的理论基础。本文基于单矢量模型预测控制、双矢量调制模型预测控制的控制误差提出了一种可视化分析方法，从理论上详细证明了双矢量调制模型预测控制方法根据目标函数值的倒数计算电压矢量作用时间的有效性，从而为调制模型预测控制的推广应用奠定了坚实的理论基础。此外，将本文所提可视化分析理论扩展到三矢量模型预测控制依然适用。详细的对比实验结果同样验证了双矢量、三矢量调制模型预测控制方法的有效性以及本文所提可视化理论分析的正确性与可推广性。

由于中点箝位型三电平逆变器、矩阵逆变器等拓扑和两电平逆变器具有类似的电压矢量分布规律，因此，在今后的研究中，可以进一步将本文所提控制方法推广应用于中点箝位型三电平逆变器、矩阵逆变器等拓扑中，并采用本文所提可视化方法分析其有效性，实现低电流谐波预测控制。

附录见本刊网络版（http：//www.epae.cn）。