潜水轴流泵叶片静力分析

王开杰 ， 赵 勇 ，安逸知 ，董 威

（1.长安大学道路施工技术与装备教育部重点实验室，陕西 西安 710064；2.山推建友机械股份有限公司，山东 济南 250000）

0 引言

潜水轴流泵属于低扬程，在喷水推进、电厂循环水工程、调水工程方面有着广泛的应用[1-2]。

轴流泵在工作中的稳定性一直是人们普遍关注的问题，流体在泵内流动时叶轮和导叶过流部件间的动静干涉作用及空化作用使得叶片受到周期性的载荷分布，这将会造成叶片的变形破坏和应力集中，并且高速旋转的叶轮叶片在压力脉动与压差影响作用下，会产生应力集中并伴随周期性变化，导致叶片沿某一方向产生位移变形[3]，从而影响到机组运行的稳定性。就轴流泵的结构特点而言，叶顶与轮缘位置之间的间隙往往很小，以避免产生泄露与回流，造成容积损失，因此必须确保叶片在工作过程中所产生的径向变形远远小于叶顶间隙，同时也要尽可能减小其他方向变形而发生疲劳破坏的风险[4]。

国内外学者对潜水轴流泵的关键过流部件叶轮的叶片开展了试验研究，或利用数值模拟的手段研究了叶片的流固耦合特性。潘旭等[5]综合考虑了轴流泵工作时叶片真实的应力及变形状态，比较分析了两种工况下叶片运行时的强度及刚度，并研究了应力集中和变形的主要位置。施卫东等[6]对轴流泵叶轮叶片在流固耦合作用下的变形和应力分布进行了计算，分析了流固耦合作用对轴流泵扬程和效率的影响。马希金等[7]分析了轴流泵叶片在流固耦合下的应力及变形集中区域，得出叶片的应力及变形分布规律。

为进一步研究潜水轴流泵内部压力脉动特性，以及在设计工况下运行时叶片承受载荷所引起的各方向位移变形，对叶轮叶片吸力面以及工作面设置旋转的压力监测点，讨论叶片在流固耦合下的静力学特性，旨在为今后泵的稳定运行提供一定参考。

1 物理模型与数值方法

1.1 物理模型

本文以某潜水轴流泵模型为研究对象，模型由以下5 个过流部件组成：进水管、喇叭管、叶轮、导叶和出水管。潜水轴流泵的基本参数为转轮直径D=280 mm，转轮叶片数为3，导叶数为5，额定转速n=1 450 r/min，设计扬程H=6.3 m，额定流量为Qd，比转速ns=1 400。

1.2 网格与数值设定

对轴流泵段进行网格划分，其中叶轮与导叶采用CFX 专用前处理网格划分工具Turbogrid 生成高质量六面体网格，而其余各域均采用Mesh 工具划分六面体网格。关于网格无关性检验以模拟计算结果中效率与扬程为指标，整个泵段计算域网格数量从125 万到450 万分为6 个网格密度，并且满足叶轮与导叶近壁区域y+＜100，最终采用220 万网格节点进行数值计算，图1 为轴流泵全流道网格无关性验证结果。其中网格节点数分布情况为：进水管18 万，喇叭管20万，导叶82 万，转轮80 万，尾水管20 万，图2 为全流道网格划分布局结果。

数值计算采用旋转机械仿真商用软件CFX，边界条件采用收敛性较好的质量流量进口与静压出口。其中进口边界的质量流量设置为Q，出口边界静压为0 MPa，整个计算域参考压力设为1atm（一个标准大气压），叶轮旋转方向基于右手定则确定。定常计算中，对于叶轮旋转部件和导叶静止部件之间交界面采用Mix plan处理。数值计算选用SST 湍流模型，并应用曲率修正选项。对于SST 湍流模型，能够很好地描述近壁面流动情况，因为在近壁区和远壁区采用了不同的算法，且对y+值要求适中，所以能有效节省计算资源。

图1 网格无关性分析

图2 轴流泵网格布局

1.3 外特性分析

图3 为5 个极偏工况下的扬程数值模拟值与试验值对比，从图中可以看出，采用数值模拟计算得到的流量扬程曲线与试验值有较高的吻合度，极偏工况下的最大相对误差在4%以内，可见虽然采用较好的网格进行整体流道三维数值计算，预测的外特性参数与模型试验还是有一定误差，但极偏工况下的数值计算与试验测量结果间误差略大也较为常见[8]。因此在一定程度上表明，采用该数值模拟仿真能够较准确地预测泵的内部流动特性，以此为基础进行进一步静力学仿真也具有一定可靠性。

2 静力学分析

根据已有文献关于压力脉动特性的研究了解到，叶片的不同位置在工作过程中承受来自水流作用下不同程度的压力动载荷，因此对于叶片力学性能提出了一定要求。叶轮叶片在设计工况下高速旋转时承受水流冲击以及离心力与重力载荷的叠加作用，于是在坐标系下将会产生可分解为三个方向的微小程度的变形以及在压力脉动作用下会产生周期性振动变形，根据叶片结构设计呈现叶根厚和叶顶薄的特点，部分位置可能会有叶片高周疲劳的风险[9]。因此，讨论泵在设计工况下的静力学特性对于泵的安全稳定运行具有重要意义。

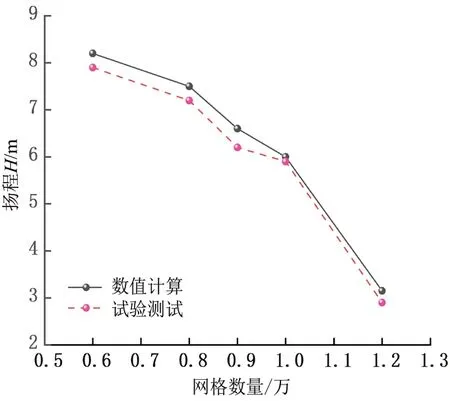
图3 扬程数值模拟值与试验值对比

2.1 结构域载荷施加

叶片是静力学分析的关键，因此对叶轮非关键部位进行简化，在叶轮结构域的静力学分析中采用四面体网格划分，并应用自上而下的Patch Independent网格划分算法，该算法将对叶轮结构中不必要的几何边界进行忽略，能产生较好的网格划分质量。图4 为叶轮固体域边界条件加载情况。叶轮结构内圆柱面设置为转动副，围绕Z 轴旋转，同时限制Z 轴向的平移自由度。由于叶轮受到离心力、流场压力以及重力作用，因此分别施加转速（离心力）载荷，方向为逆时针（沿Z 轴负方向看），同时添加标准重力加速度g=9.81 m/s2，方向向下[10]，最后导入定常计算得到的压力数据。其中，流固耦合数据传递的交界面是叶轮三个叶片表面。为确保流场计算所得的压力数据能准确传递到结构域中，叶轮中尤其是叶片部分网格划分方式和尺寸应尽量与流场中网格划分方式和尺寸保持一致。

2.2 静力学计算结果

图5 为泵设计工况运行时叶片表面位置的等效应力分布图。图5（a）为叶片吸力面等效应力分布，可以看出叶片根部且略靠近进水边位置承受应力较大，同样的，图5（b）为叶片压力面等效应力分布，与吸力面类似，但压力面的应力集中区域较吸力面更均匀。叶片最大等效应力为170.41 MPa，满足材料强度要求，因此，在此设计工况下，叶片的静力学性能能够满足要求。

图4 叶轮固体域边界条件

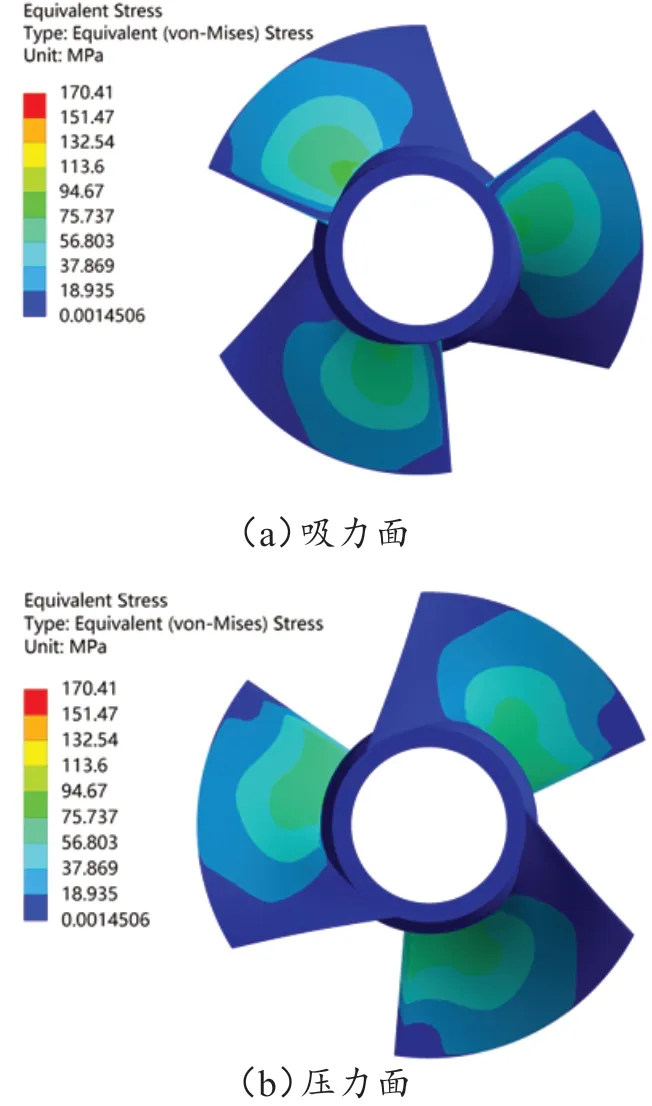
图5 设计工况下叶片的等效应力

图6为设计工况条件下叶片的各向变形，其中叶片径向变形量为三个方向最小，说明水流在叶片沿叶高方向的脉动程度较小。叶片在周向和轴向的变形相对径向较为显著，对于周向的变形可归因于水流对叶片的冲击与离心力载荷作用的影响，周向变形最大位置为叶片进口侧靠近轮缘位置，而这与叶片结构有很大关系，通常是因为叶片叶顶靠近进水边位置结构设计得很薄导致的。叶片的轴向变形量同样与结构强度有关，但轴向方向的变形大是由叶轮叶片做功机理决定的，工作时叶片吸力面与压力面大的压差是产生轴向变形的决定因素，其最大变形量达到0.040 0 mm，变形位置主要集中在叶片进口侧和远离轮毂位置处。

3 结语

1）通过对叶片表面的应力分析，可以看出叶片根部且略靠近进水边位置承受应力较大，叶片压力面与吸力面等效应力分布类似，但压力面的应力集中区域较吸力面更均匀。

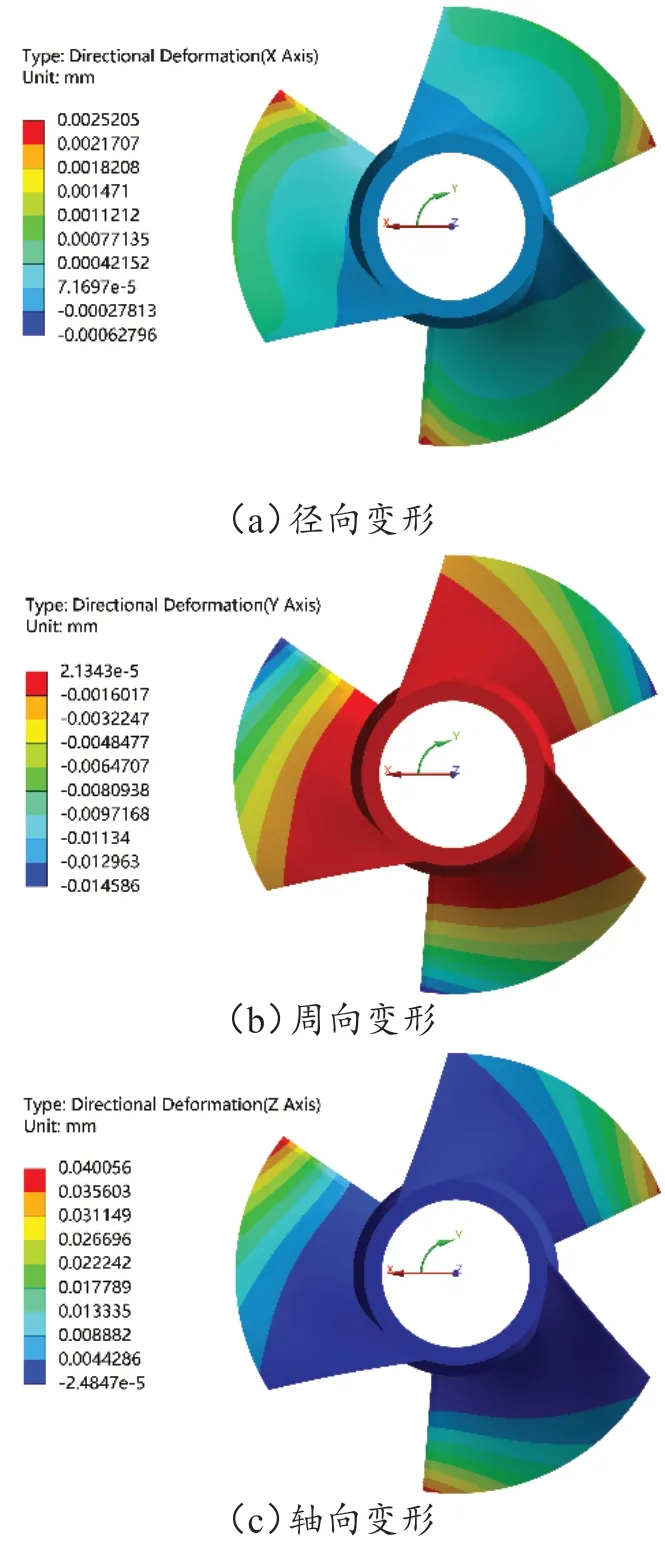
图6 设计工况下叶片的各向变形

2）叶轮叶片在承受流场压力以及离心力等其他载荷作用下，在轴向方向产生最大位移变形，其最大变形量为0.040 0 mm，表明吸力面与压力面的压差对变形占主要作用，其次是周向变形0.014 5 mm 与径向变形0.002 5 mm，且叶片在三个方向上最大位移变形均在叶片进口侧靠近轮缘位置。