初中数学培养学生逻辑推理核心素养探究

■天津市滨海新区汉沽第三中学 冯冬梅

数学核心素养可以理解为学生学习数学应当达成的有特定意义的综合性能力。数学核心素养包含数学抽象、逻辑推理、数学建模、数学运算、直观想象、数据分析六个方面。逻辑推理核心素养是其中的重要一环，也是数学教学中的重要任务之一。

数学这门学科逻辑性非常强，很多数学问题都比较抽象，所以学生不能靠死记硬背公式、定义、定理来学数学，这样学不好数学。我们知道，在解决数学问题时，要用到数学逻辑推理能力，而这种能力会影响和制约学生思维的活跃性，并会对学生的发展产生很大影响。所以，作为一名初中数学教师，有责任在教学中，注重培养学生数学逻辑推理能力。下面，谈谈在教学中的具体做法。

一、善用生活素材，增强应用能力

数学课堂教学活动要尊重学生的主体地位。教学时，要从学生的生活经验和已有的知识体验入手，创设课堂教学情境，激发学生的求知欲，增强学生对数学知识的应用能力。

例如：在学习“轴对称图形”时，学生可以举一些熟悉的例子，教师利用多媒体，把一些具有对称性的图片展示给学生：现代和古代的一些建筑，熟悉的一些昆虫，漂亮的树叶……学生从这些图片中获得美的感受。同时，教师可以利用多媒体向学生展示家乡近年新盖起来的一些高楼大厦，通过创设这样的教学情境，进一步激发学生对家乡的热爱之情。把数学知识融入生活中，学生会很自然地感受到数学的生活化，了解数学来源于生活并应用于生活。再比如：教师引导学生认识人体是轴对称的。这样的例子，能激发学生学习数学的兴趣，有利于学生理解数学知识，提高应用能力。

二、创造猜想条件，培养推理能力

义务教育阶段，数学逻辑推理能力核心素养的培养是指，通过数学学习，学生经历观察、实验、猜想、证明等数学活动过程，发展合情推理能力和初步演绎推理能力，能有条理、清晰地阐述自己的观点。

由此可知，猜想和推理是培养学生增长创造性思维的关键过程。学生在课堂上提出猜想，并验证猜想，这个过程本身就是学生逻辑推理能力提高的过程。例如：学生们在学习全等三角形的判定时，我引导学生，如图，△ABC≌△DEF，那么他们的三条边、三个角分别对应相等。反过来，由全等三角形的定义，如果△ABC 与△DEF 同时满足三条边分别相等，三个角分别相等，那么肯定可以判定这两个三角形是全等的。但是，一定要同时满足这六个条件吗？教师引导学生进行猜想：当△ABC 与△DEF 满足六个条件中的一个或两个时，能否判定他们全等？学生经过验证得出不能判定其全等的结论。那么，若两个三角形满足三个角分别相等，他们全等吗？学生经过举反例得出不一定全等的结论。那么，对于三个条件来说还有可能是三边对应相等或者是两条边及一个角（角的位置没有确定）分别相等，还有可能是两个角及一边（边的位置没有确定）分别相等。满足这些条件的两个三角形一定全等吗？这样，学生在教师的启发引导下，经过猜想再进行验证，这种做法会对培养学生的逻辑思维能力有很大帮助。

三、重视基础教学，提升思维空间

在数学教学中，要重视基础教学和概念性教学，因为只有数学基础打牢了，学生的逻辑推理能力才有提升的空间。在讲解基础知识的时候，教师可以同时渗透逻辑推理的方法。

例如：学习了“幂的运算”基本内容后，学生利用基本法则可以完成一些运算。为了提高学生的逻辑思维能力，我布置了一道这样的习题：若8m×42m-1÷23m+1=16，求m的值。经过观察、分析，得知此题主要考查幂的乘方、同底数幂的乘、除法知识，还考查了学生的数学思想——方程思想的应用。经过观察分析学生得到结论：可以把等号左边转化成以2为底的幂的形式，这样原等式就可以转化为：23m×22(2m-1)÷23m+1=24，之后，学生就可以独立完成了。这类题对提升学生的逻辑推理能力有很大帮助。

为了让学生进一步加强练习，我又布置了一道习题：若4x=2，4y=3，求162x-y的值。这道题考查了学生的逆向思维，对提升学生的思维空间具有积极作用。如果学生的运算法则、基本概念不清楚，那么提升学生的逻辑思维就是天方夜谭。

四、强化推理训练，提高思维敏捷度

在课堂上，进行强化推理能力的训练，提高学生的思维敏捷性，从而进一步培养数学逻辑推理能力。例如：教学“全等三角形”后，出示练习题：如图，已知：在△ABC 中，BA⊥CA，AC=AB.直线m 经过点A，BD⊥直线m，CE⊥直线m，垂足分别为点D、E。求证：DE=BD+CE。

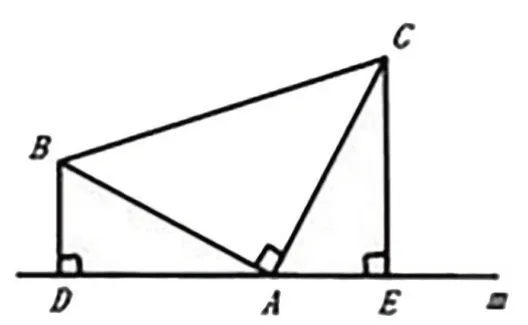
几何证明题通常需要“从后往前”分析：要证明DE=BD+CE，结合图形，可以得到DE=DA+AE。所以下面只要证BD=AE,DA=CE 即可。由此，可以想到，只要证明△BDA≌△AEC 就行了。结合已知：BD 和直线m垂直，CE和直线m垂直，从而可以得到∠BDA=∠AEC=90°。已知AB=AC，那么，只要再找出一个条件就可以证明△BDA≌△AEC。根据“多垂直”，所以我们可以利用“互余”的知识，证出两个锐角∠BAD=∠ACE 或∠DBA=∠CAE，从而可以证出△BDA≌△AEC。再结合全等三角形的性质：全等三角形的对应边相等，得到BD=AE，DA=CE，可以证出DE=DA+AE。学生清晰地分析出了证明思路，证明过程就会顺利完整地写出来。由此，要加深学生对数学知识的理解，提高其思维的敏捷性，就要强化学生数学逻辑推理能力的训练。

五、规范数学语言，促进思维发展

有的学生上课回答问题时，思维混乱，说话层次不分明，导致回答问题后，其他学生不理解，回答问题的学生还特别着急。显而易见，这样的学生数学语言不严谨，说话缺乏逻辑性。

在学习线段垂直平分线的性质定理时，有的学生经常这样记忆：线段垂直平分线上的点到角两边的距离相等。很明显，其混淆了概念。再比如：在进行几何证明时，首先要进行分析：题目要证明什么结论，由已知可以知道哪些条件，还需要哪些条件，应该怎么证明这些未知的条件。这样，逐步进行证明，就不会出现思维混乱的情况了。通过对几何证明题的分析，数学语言规范、严谨了，学生在证明过程中明白了应该怎样表达自己的数学解题思路，知道了应该先写哪一步，后写哪一步。经过一段时间的训练，肯定会促进学生的思维发展。

六、贯彻建模思想，关注思维过程

众所周知，函数作为研究现实世界中变量之间关系的模型，对于初中生来说比较抽象和不易理解，但是在解决实际问题时很有用。所以，在数学教学中，教师一定要注重函数基础知识的教学，建立模型思想，关注学生的思维过程。

例如：有这样一道题：用长为24 米的篱笆围成一个长方形的鹅场，一面靠墙（墙的最大可用长度a 为10米），鹅场的宽AB为x，面积为S。（1）求S与x 之间的函数关系式并求出最大面积是多少？（2）如果要围成面积是50平方米的养鹅场，求AB的长？

经过分析得知，此题建立起了二次函数与实际问题之间的联系，检测了学生对二次函数解析式的确定、二次函数的最值问题、二次函数与一元二次方程之间的关系知识点的掌握情况。根据长方形面积公式，已知宽为x，周长为24，一边靠墙，从而有一条长边，三条宽，则长方形的面积S=x（24-3x），求出了S与x之间的函数关系。由此可见，二次函数的基础知识是解决这类问题的关键点，这道题关注了学生的思维过程。

在核心素养背景下，数学教学的关键内容是培养学生的数学逻辑推理能力。数学逻辑推理能力代表着一种数学思维。在学习生活中，学生会遇到很多问题，这些问题都可能与数学逻辑推理能力相关。在数学教学中，教师应注重对学生数学逻辑推理能力的培养。