保护隐私的集合相似性度量协同计算协议
逯绍锋,胡玉龙,逯跃锋
(1.东北大学 计算机科学与工程学院,辽宁 沈阳 110189;2.中国交通通信信息中心,北京 100011;3.山东理工大学 建筑工程学院,山东 淄博 255049;4.中国科学院 地理科学与资源研究所资源与环境信息系统国家重点实验室,北京 100101)
0 引 言
机器学习(Machine Learning,ML)作为一种实现人工智能的方法,主要是通过算法来解析数据,不断学习,进而对事物做出判断和预测[1]。机器学习广泛应用于计算机视觉、语音识别和自然语言处理等领域,是近些年学术研究上的重要方向。然而,蓬勃发展的机器学习技术在给人们带来便利的同时,也使数据安全与隐私面临更加严峻的挑战[2]。目前,研究人员提出了许多解决机器学习中的隐私问题的方法[3-6]。
解决隐私保护的安全多方计算(Secure Multi- party Computation,SMC)由Yao在文献[7]中首先提出。在安全多方计算中,参与方将各自的隐私数据输入到一个约定函数进行协同计算,可以实现保证参与方的原始隐私数据不被泄露的同时,输出正确计算结果[8]。SMC作为近年来密码学界的研究热点,被认为是解决协同计算问题中保护数据信息隐私的一项核心技术[9-10]。利用SMC来实现保护隐私的机器学习由Goldwasser在CRYPTO2018上提出[11],可以在机器学习的明文架构中引入安全多方计算技术实现隐私保护。
在机器学习、数据挖掘等领域,一般都是通过计算样本间的距离来完成对样本数据的相似性度量[1]。采用什么样的方法来计算两者间距离,需要根据实际进行选择,计算结果直接影响到匹配的准确与否。比如采用欧氏距离计算两者之间的空间距离,使用汉明距离来度量两个文本或者图像之间的差异,使用杰卡德距离(Jaccard distance)来度量两个集合之间的相似程度等[12]。文献[13]对DNA序列进行0-1编码,以GM加密方案为主要工具,通过计算两序列的汉明距离的隐私保护方法,解决了保护隐私的DNA序列比较问题。保密的集合计算是安全多方计算的一个重要方向,文献[14]针对参与者集合为有限集合子集的问题,根据Diffie-Hellman的密钥分配方案基于离散对数困难性,给出一个具体的适用于有限集合子集的交集计算协议。文献[15]针对恶意模型下多方集合交集基数计算问题,提出了一个有效的计算协议。文献[16]通过对任意有理数进行特殊的编码,将有理数域上元素与集合关系问题转化为整数范围内的向量内积问题,以Paillier加密方案为主要工具,将两方集合保密计算推广到有理数领域。文献[17]提出了计算集合运算统计量的专用安全计算协议,可以在不泄露交集元素的情况下高效计算集合交集、并集及交集权值和等统计量,解决了隐私保护集合运算解决方案单一性问题。尽管人们针对隐私保护集合及机器学习已经研究并提出了一些安全多方计算解决方案[18],但关于保护隐私的集合相似性度量问题,在当前的文献研究中尚未发现。该文尝试通过解决杰卡德距离的安全多方计算问题,来进一步解决关于集合相似度计算的隐私保护问题。
1 相关知识
1.1 半诚实模型下协议的安全性定义
Goldreich在文献[19]中指出:半诚实模型中的参与者会诚实地执行协议,但他们会根据自己在协议执行过程中获得的信息对其他参与者的秘密数据进行推导,下面给出半诚实模型下的安全性模拟范例。
设分别持有秘密数据x和y的协同计算参与者A和B,一起执行协议π,协同合作计算函数f(x,y)=(f1(x,y),f2(x,y))。协议执行中参与计算双方获得信息序列为:
(1)
(2)
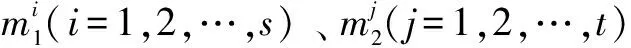
定义:在半诚实模型下,对于计算函数f的协议π,如果存在概率多项式时间算法S1与S2,使得:
(3)
(4)
1.2 杰卡德距离
在机器学习中估算不同样本集合之间的相似性时,通常要计算样本之间的相似度,将这一类集合之间相似度统称为集合距离。其中,最常用到的集合距离就是杰卡德距离。实际上,杰卡德距离和杰卡德相似系数互补,是通过计算集合间的交集和并集的基数来完成对两个集合的相似性衡量的一种集合距离。
杰卡德相似系数[12]实际就是两个集合交集大小与并集大小的比值(见图1):

图1 两集合的杰卡德相似系数
(5)
杰卡德距离与杰卡德相似系数互补,其公式可推导如下:
(6)
由于集合容斥原理,|A∪B|=|A|+|B|-|A∩B|,因此杰卡德距离公式可以推演为如下公式:
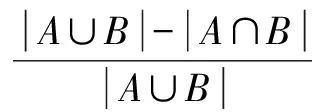
(7)
1.3 异 或
异或是一种基于二进制的位运算,该文用符号⊕表示,其运算法则是对运算符两侧数的每一个二进制位,同值取0,异值取1。如表1所示,可以得到异或运算具有下面的性质。
性质1:对于一个数,存在与0异或值不变的恒等特性。

表1 异或运算
性质2:对于一个数,存在与自身异或值为零的归零特性。
1.4 GM同态加密方案
GM同态加密方案是Goldwasser与Micali在文献[20]中提出的一种概率加密方案。
系统建立。系统选取N=pq,其中p,q为两个大素数,y为模N的非二次剩余。系统公钥为(N,y),私钥为(p,q)。
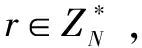
解密过程。密文c 明文: (8) 性质3:GM加密方案具有异或同态性质。 证明:设E是一个加密算法,c1=E(m1,r1)是对m1的加密,c2=E(m2,r2)是对m2的加密,若有c1c2=E(m1⊕m2,r),其中r1,r2,r是随机数,⊕表示异或,则称E是一个异或同态加密算法。在Goldwasser-Micali方案中,令r1r2=r,则有: gm1⊕m2(r1r2)2modN=gm1⊕m2r2modN (9) 即有,E(m1)E(m2)=E(m1⊕m2,r)。因此,GM加密方案具有异或同态性质[10,20]。 性质4:GM加密方案具有自反性质。 证明:根据前文所述异或运算的性质,对GM加密方案进行异或同态操作时有: gm1⊕m2⊕m2(r1r2)2modN= gm1⊕0r2modN=gm1r2modN (10) 即经过两次对同一密文的异或,可使得密文c1变成另一个密文c1c2c2,但不影响解密的明文m1。因此,由以上推理可得到:在GM加密方案中,异或具有自反性质。 集合距离计算是机器学习、人工智能等领域的一个基本问题,由于经常会用到敏感信息,因此就不得不考虑参与计算各方数据的隐私问题。进而研究如何在保证各参与方数据隐私的前提下进行集合距离计算也变得十分必要,该文将保护隐私的集合距离问题描述如下: 问题描述:假设Alice输入集合数据D1,Bob输入集合数据D2,Alice和Bob想要共同协作计算出D1和D2两个集合的相似度距离,同时又不泄露各自的元素数据信息。 问题转化:为了更好地解决上述问题,该文采用如下称之为位置编码的方法,对参与计算的数据进行处理。假设存在集合U={x1,x2,…,xi,…,xn},i∈[1,n]为一个全集,|U|=n。Alice拥有集合D1={a1,a2,…,ai,…,an1},其中ai∈U,Bob拥有集合D2={b1,b2,…,bj,…,bn2},其中bj∈U,该文将集合元素按照以下规则先行进行编码: (11) 下面以具体的例子来说明问题转化过程。 例1:假设存在全集U={a,b,c,d,e,f,g,h,i,j,k,l}及两个集合D1、D2,分别为:D1={f,a,c,e}、D2={f,a,c,i,l}。对集合D1按照前文规则(11)对其编码,可得到新的编码集合为A={6,1,3,5},同样,对集合D2编码之后对应的编码集合为B={6,1,3,9,12},如表2所示。 表2 对集合进行位置编码 计算原理说明:经过分析发现,D1和D2两个集合经过位置编码后,计算D1和D2两个集合的相似性度量问题就转化为求A和B两集合的相同数字个数问题。 该文通过对转化后的问题设计具体协议进行解决,实现保护隐私的集合相似性度量协同计算。对编码后的两集合中的数字先进行逐位异或运算,再根据异或运算的归零率特性,一个数与它本身进行异或运算等于零,否则为非零,求出两个集合异或运算后新的集合中的零的个数,即可求出A和B两集合相似性度量值,对基数较小集合,不足部分补零。例如,在上述例1中两个集合D1和D2经过位置编码后,再进行逐位异或运算的结果为:C={0,0,0,1,1},结果集中0的个数为3,从而可知D1和D2两个集合的相似性距离值为1/2。 协议1:保护隐私的集合杰卡德距离协同计算协议。 输入:Alice和Bob分别输入私密的集合: D1={a1,a2,…,ai,…,an1},D2={b1,b2,…,bj,…,bn2},其中ai∈U,bj∈U,U为包含集合的全集。 输出:两集合的杰卡德距离Jd。 (2)Bob生成自己的GM加密系统的公钥为PK=(δ,n),私钥为SK=(p,q)。 (3)Alice将收到的E(A)和E(B)两两相乘,并进行同态操作: C=E(A)E(B)= E(A⊕B)= {E(c1),E(c2),…,E(cm)} (4)Alice选取随机置换T对上述结果进行置换,得到随机置换后的m个密文: 并将该密文发回给Bob。 (5)Alice计算自己集合的基数CA=|D1|,随同之前E(A)一并发给Bob。 步骤3:(1)Bob收到置换后的m个密文后,进行逐次解密,得到: (3)Bob计算集合的大小值CB=|D2|,并完成两集合的杰卡德相似性值计算。 (4)Bob将Jd值传送给Alice。 分析:在协议1中,由于Bob发送给Alice的是自己对集合D2进行位置编码后的密文E(B),其他合作计算方不能解密,因此也不能从中得到集合D2的隐私信息。另一方面,Alice将自己的集合D1进行位置编码并加密后获得E(A),两者相乘后得到E(A)E(B)=E(A⊕B),若直接将计算结果传给Bob,由于Bob可以解密得到A⊕B,在这个基础上,Bob就可以通过加密机制的自反特性A⊕B⊕B得到A,从而得到Alice的隐私集合D1的信息。因此,为了防止这种隐私泄露,Alice将E(A⊕B)随机置换得到(E(A⊕B))T,这样使得Bob解密后只能得到(A⊕B)T,由于置换函数为Alice独自掌握,因此Bob无法从中获取到A的信息,从而Alice保护了自己的隐私。 根据GM的同态加密方案的异或同态性,任何数字对自身进行异或结果为零。并且在协议第3步虽然进行了置换,但置换前后集合中零的总数是不变的,即: (12) 由于CA=|D1|、CB=|D2|的值不变,因此所得Jd的值即为两集合的杰卡德距离值。协议1是正确的。 定理1:协议1能够保密地协同计算出两集合的杰卡德距离值。 证明:下面用模拟范例的方法来严格证明协议的安全性。 首先,构造模拟器S1,令f1(A,B)=f2(A,B) =Jd(A,B),并将(A,f1(A,B))输入S1。 具体步骤如下: 第2步:S1将集合D1进行位置编码得到: 然后,再逐位加密,得到n长密文: 然后将收到的E(B')和E(A')两两相乘,并进行同态操作: C=E(A')E(B')= E(A'⊕B')={E(c1),E(c2),…,E(cn)} S1选取随机置换T对上述结果进行置换,得到随机置换后的n个密文: 第3步:将此n个密文逐次解密得到: 即两集合的杰卡德距离值: 在本协议中, E(B')。 又因为E(C)=(E(A)E(B))T,E(C')=(E(A)E(B'))T,且随机置换为同一置换T,从而可知: 因此可得: 同理,用类似的方法可以构造模拟器S2,使得: 因此,协议1可以保密地协同计算出两集合的杰卡德距离值。 计算复杂性。文中协议借助GM同态加密方案来解决问题,计算开销主要来自于模乘运算,因此以模乘运算次数作为衡量指标。在协议1中,Alice执行加密m次,Bob执行加密、解密各m次,由GM同态加密方案可知,加密一次需要2次模乘运算,解密一次需要logp(p为GM同态加密方案中的大素数私钥)次模乘运算,而m≤n,因此协议1最多需进行4n+nlogp次模乘运算。 通信复杂性。一般用协议交换信息的比特数或者通信轮数作为衡量通信复杂度指标,在安全多方计算中通常用轮数[10]。在协议1中,计算双方共需进行两轮通信。 文献[13]基于GM同态方案解决汉明距离,经过改造后也可用于计算集合相似度,但文中协议要对数据长度进行扩展,因此协议双方计算共需要做4n(4+logp)模乘运算,但协议同样需要2轮通信。 文献[14]提出协议4经过变形后可保密计算两个集合交集的基数,用于集合相似度评价。该协议是借助Diffie-Hellman的密钥分配方案设计的解决方案,协议中计算双方共需要做4n次模乘运算,进行3轮通信。 协议效率分析比较如表3所示。 表3 协议效率分析比较 从协议1可以看出,协同计算的核心是求解参与计算的两个集合的交集的基数,通过对协议1的必要改造后,可以构建其他类似的保护隐私的相似性度量协同计算协议,完成对Dice系数、Tversky系数、集合余弦相似性的计算。 Dice系数最初是被用来定量表达两个不同物种在自然界中的关联程度[21],作为一种集合相似度度量函数,如今被广泛应用于深度学习图像分割和目标检测中。其公式含义可解读为真实数据集和预测数据集中的正确部分之和占两者之和的比例,具体公式如下所示: (13) Tversky系数是由Tversky等在文献[22]中提出的用于特征相似性测度的函数,杰卡德系数和Dice系数均是Tversky系数的参数取特定值时的一种表达。 (14) 余弦距离和余弦相似度互补,集合的余弦距离是通过计算两集合夹角的余弦值作为衡量两个集合之间的相似性的一种方法[12],具体公式如下: (15) 事实上对于文本相似性也可以借助shingling算法将文档转化为集合,再借助文中协议进行保密协同计算出其相似性[23]。对于海量数据,可以借助最小哈希和局部敏感哈希[24]寻找相似集合的算法实现数据的相似性度量保密协同计算。 集合相似性度量问题是机器学习领域的基本问题之一,在能够保护隐私的前提下计算两集合对象间的相似性距离值是密码学中一个新的问题,在机器学习、图形识别、人工智能、生物信息学等方面有着重要的应用。该文设计了一种新的编码方法,将相似性度量问题转化为计算两集合相同数字个数的问题,使集合相似性度量距离计算问题普适化,并结合异或的思想,借助同态加密算法来解决杰卡德距离计算的隐私保护问题。然后,用模拟器证明了该协议是安全的,并分析了协议可以高效安全地计算两集合对象间的杰卡德距离。最后,将问题扩展至其他方面,证明该协议具备一定的普适性,经过必要的改造后可以解决保密计算Dice系数、Tversky系数、集合余弦相似性等问题。由于该协议仍是基于半诚实模型,恶意模型下的保护隐私的集合相似性度量协同计算问题将是后续研究的方向。
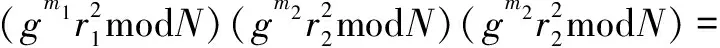
2 问题描述及转化


3 具体协议

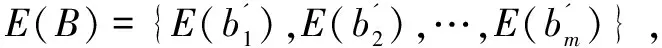



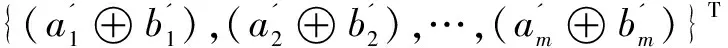

4 协议分析
4.1 正确性分析
4.2 安全性分析






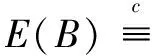
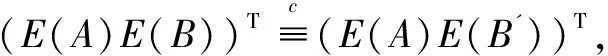
4.3 计算与通信复杂性分析

5 文中协议应用推广
6 结束语

