基于组合模型的服装定制面辅料预测方法

赵 鑫，毋 涛，宋 田，甘 霖

(1.西安工程大学 计算机科学学院，陕西 西安 710600;2.山东如意毛纺服装集团股份有限公司，山东 济宁 272000;3.陕西服装工程学院，陕西 咸阳 712046)

0 引 言

服装企业面辅料库存来源于采购，而采购量往往受客户大幅度波动影响导致大量呆滞库存的产生，另外，海外料多、专用性强的特点拉长了采购周期，给企业降库存带来很大的压力[1-2]。近几十年来，很多国内外学者对时间序列预测做了大量相关研究和应用。目前，对服装面辅料需求时间序列的预测研究相对很少。

李科君等[3]构建了非线性自回归神经网络模型对地铁进站客流进行短时预测；唐继强等[4]根据客流季节特征建立季节时间序列并采用自回归差分滑动平均模型来预测轨道交通客流；李亭立等[5]提出了基于Prophet算法的服装面料需求预测模型来解决目前服装面料需求数据周期非确定性导致预测精度差的问题；袁远等[6]提出结合ARIMA与RF模型的销售预测模型来帮助快销服饰企业制定合理的生产销售计划；Goyal Megha[7]利用ARIMA模型对印度农产品出口进行预测；郜珍[8]利用ARIMA模型对国内服装往国外销售的出口量变化趋势进行了预测分析，并对出口量总额进行了预测分析；Chao Yan等[9]通过将通过截断奇异值分解(SVD)从服务质量矩阵中提取的压缩矩阵与经典的ARIMA模型相结合，扩展了ARIMA模型以同时有效地预测多个服务质量值；张国赟[10]等加入遗传算法来优化ARIMA模型，随着迭代次数的逐步增长，数值会更快地趋于稳定状态并且达到最优值；刘敏等[11]构建了GS-ARIMA(6,1,5)预测模型对原油股票的成交量进行预测分析；王艳[12]使用GARCH模型对国内的石材生产量进行了分析预测，其中GARCH模型可以将异方差预测问题进行较好的处理。

通过上述研究表明，时间序列预测方法在预测方面具有明显的优势。然而，目前对服装面辅料需求量进行预测的研究相对较少。该文通过引入GARCH模型来消除残差序列中出现的异方差现象，相比其他时间序列预测模型，面辅料需求量预测效果更好且精度更高。

1 相关理论

1.1 ARIMA模型

ARIMA[13]模型在研究中使用热度很高地针对时间序列进行预测的模型，它的三部分组成分别是AR模型、MA模型和差分过程的阶数I，故也称其为自回归滑动平均模型，可以简写为ARIMA(p,d,q)模型。如果变化为一个平稳的时间序列可能需要通过d次的差分过程，那么ARIMA(p,d,q)模型如公式(1)所示：

(1)

其中：

Φ(B)=1-Φ1B-Φ2B2-…-ΦpBp

(2)

θ(B)=1-θ1B-θ2B2-…-θpBp

(3)

式中：|B|≤1并且Φ(B)和θ(B)相互为质，Φpθp≠0；Φ(B)为自回归表达式；θ(B)为移动平均表达式；{εt}为白噪声均值为零的时间序列。

时间序列的平稳化是构建模型的前提，构建模型时可以使用差分法在时间序列展现相对稳定的形式时使时间序列趋于稳定化，并且按d阶差分的方法可以得到新的ARIMA模型。

1.2 GARCH模型

GARCH[14]模型是通过借助于过去的时间序列变化趋势和方差结果对未来短期内的时间序列预测变化趋势，特别适合用于波动性时间序列的分析和预测，故也称其为广义自回归条件异方差模型。误差结果在时间段m的方差结果值和前一时间段m-1的残差平方和之间存在着相互依赖的关系。通过使用GARCH模型替换ARCH模型可以提高模型的预测准确性以及对模型参数取值的估计更为容易；GARCH模型兼具ARCH模型的所有优点，并能获取到时间序列变化趋势的平缓期和波动期。

GARCH模型一般含有两个最为关键的方程：第一个是均值求解方程，如公式(4)所示；第二个是方差求解方程，如公式(5)所示。

均值方程：

Yt=F(t,Yt-1,Yt-2,…)+ut

(4)

式中：F(t,Yt-1,Yt-2,…)为时间序列{Yt}的确定信息拟合模型。

方差方程：

(5)

GARCH模型通过比ARCH模型更少的差分阶数来达到对模型参数的更加有利的估计，并且GARCH模型将时间序列模型中异方差现象带来的影响进行分析考虑，可以在因变量求解方差结果时达到更为精准的预测效果。同时可以在均值求解过程中提高对参数更为有效的估计，从而使得时间序列在进行预测时更加精准，提升预测结果的可信度。

1.3 网格搜索

网格搜索[15](Grid Search，GS)是一种通过列举所有可能会出现的结果的方法，通过在参数范围内的每一个数据维度上进行若干等份的划分，计算时只需要遍历参数范围内每一数据维度所形成的网格相交点，利用交叉验证这种优化求解方法对函数中需要估计的参数取值进行优化，从而获取到函数参数的最优值。将所有参数存在可能的取值情况分别进行交叉排列组合，形成对应的“网格”组合结构，然后用每一组组合参数对预测模型进行训练，并通过交叉验证这种优化求解方法对模型的预测结果进行分析评估。最后，将估计函数在所有的组合中选择一个最为合适的“网格点”作为模型参数，自动将模型参数调整到最优的一个过程。

1.4 平稳性检验和白噪声检验

ARIMA模型检验方法主要有两种，一种是对模型的平稳性检验，对数据预处理后得到的时间序列数据，通过差分法对数据进行转换。通常是对拟合模型的早期数据值进行检验，目的是判断这些数据是不是能够呈现稳定状态。使用自相关函数检验的方法，因为这个方法是基于之前的时间断点间隔数据与真实数据之间的距离越大，对真实数值的干扰就越小，随着时间的逐步延长，自相关函数的参数会在不同的时间节点下逐步变小，最后逐渐减少到零，此时就证明模型拟合的数据能够呈现出稳定状态。常用的平稳性检验的方法是图像法和单位根检验。

另外一种方法通常是利用白噪声检验方法对预测模型的残差效果进行检验，依据的原理与自相关性原理相同，是在模型拟合完成时进行。通常先假定预测模型在进行检验时所产生的残差效果是符合白噪声检验的条件，然后再判断拟定的正确性，使用的是Q检验方法。如果得到的Q值很小，那么就证明模型的残差序列是几乎趋近于零的，符合假设，即表示模型符合白噪声原理。如果P值小于0.05或等于0，说明该时间序列不是白噪声数据，数据有价值，可以继续分析；反之如果大于0.05，则说明是白噪声序列，是纯随机性序列。常用的检验统计量为Box-Pierce统计量，如公式(6)所示。

(6)

1.5 AIC准则与BIC准则

赤池信息准则(AIC)，是一种对预测模型所产生的拟合效果进行评判的标准，它是通过熵的含义进行定义的，并且提供了对预测模型的复杂性和拟合数据效果进行评估的评价准则。AIC定义如公式(7)所示：

AIC=2r-2ln[L]

(7)

式中：r为预测模型中参数的数量，L为模型的极大似然函数。如果从全部可供选择的模型参数中选择最佳参数，一般会选择AIC最小的参数作为模型的参数。AIC提高了模型的拟合程度，并且将惩罚项引入其中，使预测模型中含有尽可能少的参数，这样有利于降低模型发生过度拟合的概率。

贝叶斯信息准则(BIC)，通常用于模型参数的选择。通过增加预测模型的参数数量将会导致模型变得更为复杂，从而导致过度拟合现象发生的概率提高。为了解决这个问题，AIC和BIC都增加了惩罚项来处理这一问题，但是AIC准则的惩罚项取值要比BIC准则的小很多。可以在预测样本数量较多时，高效地防止和避免由预测模型的预测结果精度过高而引发模型本身复杂度过高的情况，可以有效地解决这个问题。BIC定义如公式(8)所示：

BIC=rln(n)-2ln[L]

(8)

式中：r为预测模型中参数的数量，n为预测样本的总数量，L为模型的极大似然函数。rln(n)为惩罚项，可以在参数维度较大和训练的预测样本总数据量比较少的情况下，更有效地防止参数维度灾难的发生。

从AIC准则和BIC准则的计算公式中可以看出，它们表达式的后面半截是一模一样的，表达式的前面半截分别定义了对应准则的惩罚项取值，当n≥8时，rln(n)≥2r，所以，在对海量数据进行预测时，AIC准则比BIC准则对参数的惩罚值要小很多，这也使得BIC准则更趋向于去挑选模型参数更少的简单预测模型。

1.6 模型评价指标

该文采用了两个常用的误差评价方法，分别是均方根误差法(RMSE)和平均绝对误差法(MAE)，进行改进模型前后预测结果的比较分析，其计算公式如式(9)和式(10)所示：

(9)

(10)

2 服装面辅料需求量预测问题模型

2.1 构建面辅料需求量GS-ARIMA-GARCH预测模型

通常服装面辅料需求量预测的数据规律性较弱，需求量数据会随着不确定性误差的产生而出现比较大的变化，ARIMA模型可以很好地对因变量和误差的滞后值以及当前样本数值进行较好的预测。针对参数值随机选取的不确定性以及ARIMA模型的残差结果存在异方差的情况，引入GARCH模型来消除ARIMA模型中的异方差现象。该文构建了GS-ARIMA-GARCH组合模型来对面辅料需求量时间序列进行预测分析。根据网格搜索的思想，将参数范围进行网格化，构成组合参数区间。在对模型进行参数最优组合寻找的过程中，对预测模型进行反复训练，并利用AIC和BIC对网格中的每一个组合参数进行有效地评估，从而使得预测模型寻找到最佳的参数组合，并提高预测模型的性能和准确度。

2.2 服装定制面辅料需求量预测流程

第一步，先处理时间序列数据，使其趋于稳定，采用的方法是单位根方法检验；第二步，处理剩下不稳定的数据让这些数据也能逐步稳定，采用的方法是差分法；第三步，判定判断使用差分法解决后，再次采用单位根方法检验，直到可以说明该面料时间序列是一个平稳时间序列，可以进行建模工作；第四步，需要针对残差进行白噪声检测；第五步，根据AIC和BIC最小准则对ARIMA模型和GARCH模型进行定阶；第六步，利用模型对面料时间序列进行预测，并对预测结果和实际值进行对比分析。GS-ARIMA-GARCH模型的服装面辅料采购量预测流程如图1所示。

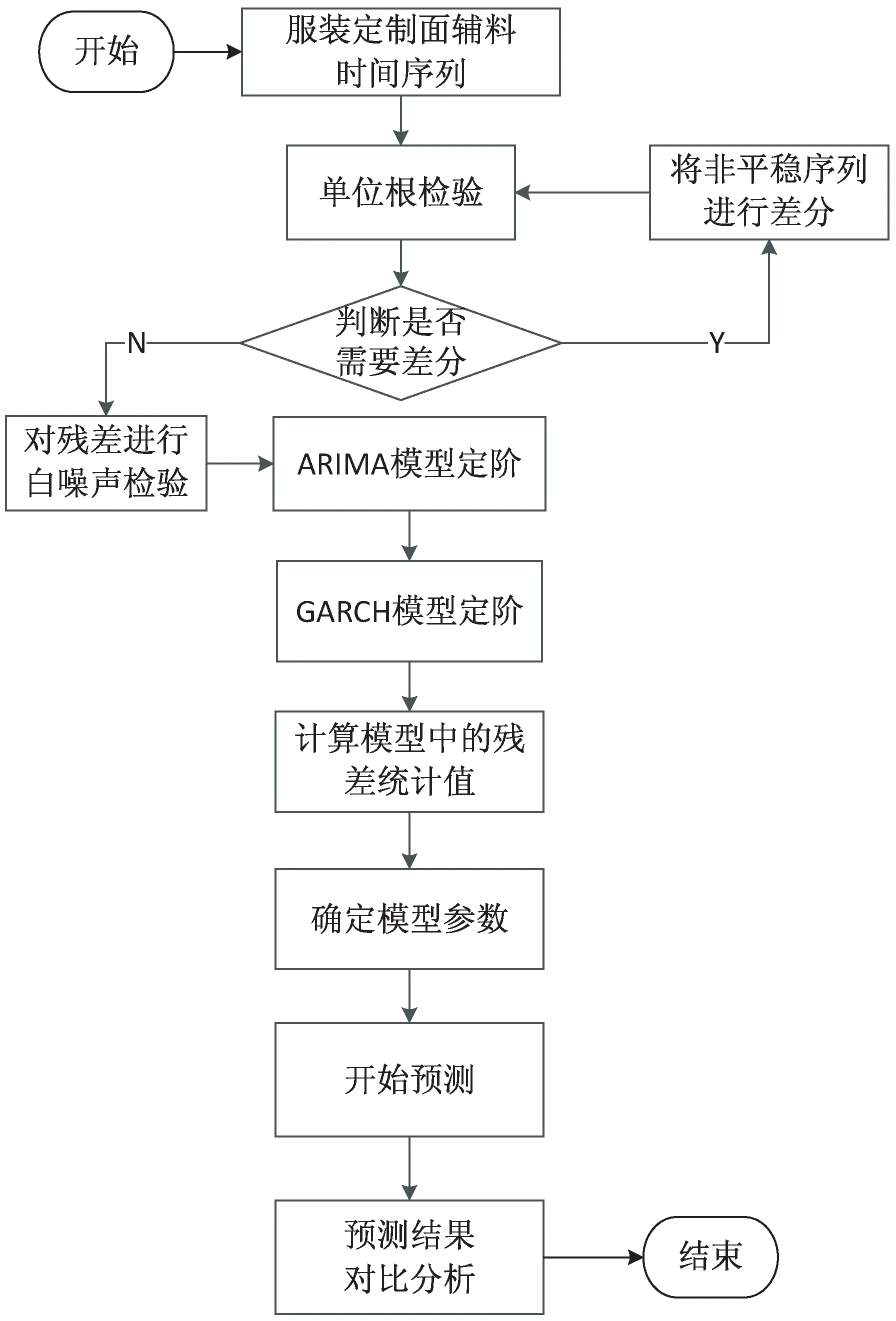
图1 服装定制面辅料需求量预测流程

3 实验过程与结果分析

3.1 实验环境

(1)硬件环境：英特尔Corei5-6300HQCPU@ 2.30 GHz处理器，16 G内存，512 G固态硬盘。

(2)软件环境：Windows10系统，PyCharm2019社区版。

(3)编程语言：Python3.7。

3.2 数据预处理

该文选取上海FL有限公司面辅料历史原始使用数据，以面料887.601-5730作为研究对象，详细信息如表1所示。

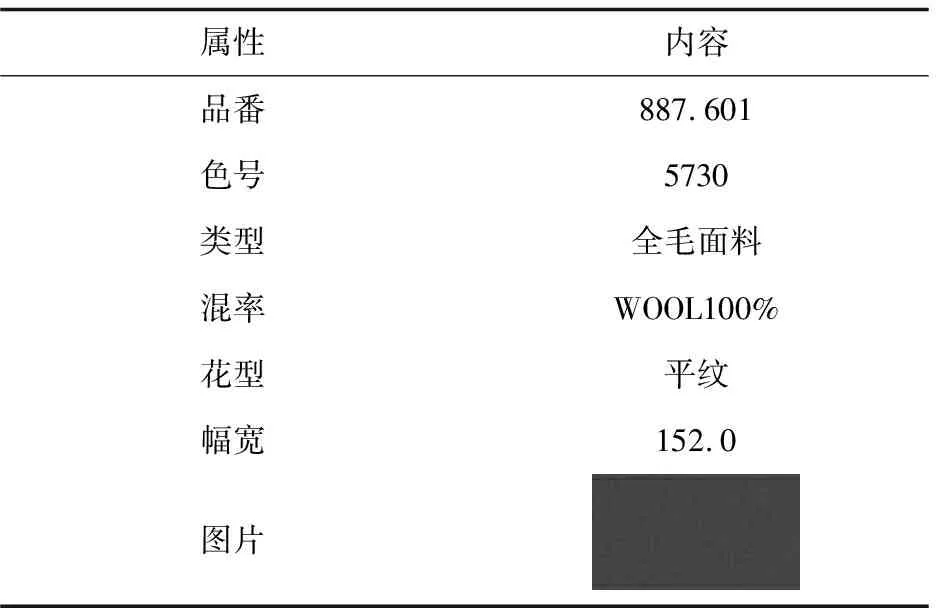
表1 面料887.601-5730详情

选取2006年至2021年面料887.601-5730需求量数据进行研究。首先，按月统计面料需求量；然后，对原始面料时间序列数据集进行数据类型不符处理、空缺值处理等前期数据预处理工作，得到面料时间序列数据。其中，面料需求量原始序列时序图如图2所示。可以看出2020年1～4月左右受全球新型冠状病毒影响，面料需求量呈现较大幅度下降趋势。对共计190个数据进行划分：前180个数据(2006年1月至2020年12月)用于建立预测模型，最后10个数据(2021年1月至2021年10月)用于验证组合模型，将组合模型获取到的预测值和面料原始实际值通过评价指标进行比较分析，以此来证明组合模型预测结果的精准性以及组合模型在进行面料需求量预测时的可靠性。

图2 面料需求量原始序列时序图

3.3 平稳性检测和白噪声检测

运用ARIMA算法前要对训练集进行平稳性检测以及白噪声检测，因为该算法只适合用在具有稳定特性和符合白噪声原理的时间序列上。对面料原始时间序列使用单位根方法进行检测，结果如表2所示。

表2 面料原始时间序列ADF检验结果

通过表2中的面料原始数据ADF检验结果可得出ADF值为-4.037 729，与3个level临界值相比结果更小，可说明该面料时间序列是一个平稳的时间序列，最终确定组合模型的差分阶数d参数值为0。同时P值为0.001 225<0.05，说明白噪声检验拒绝了原假设，确定了该面料时间序列是非白噪声时间序列，也说明了该残差序列中存在着异方差现象，通过采用GARCH模型对残差序列进行建模，从而去除存在的异方差现象。因此，该面料时间序列可以进行下一步建模工作，也表明该序列存在往下研究的意义并且可以利用ARIMA模型对其进行建模预测。

3.4 模型识别与定阶

基于信息定阶准则，可采用AIC、BIC等信息定阶分值计算公式，构建自回归模型和移动平均模型等定阶热力图进行网格搜索，对AR和MA模型进行定阶。

依据AIC最小准则，取得的最佳组合参数为AIC(1,1)。根据网络搜索思想并结合BIC准则在p～(0,3)、q～(0,3)中使用超参数对其进行优化，得到的热力图如图3所示，其中黑色位置是最好取值，通常状况下取值是越小越好。参考热力图数据和AIC最佳参数组合最终可以确定模型的参数p值为1、q值也为1。以此来确定(1,0,1)为GS-ARIMA-GARCH组合预测模型中ARIMA的最合适参数。通过多次尝试计算，使得AIC或者BIC的阶数最小，即为最适合数据的阶。

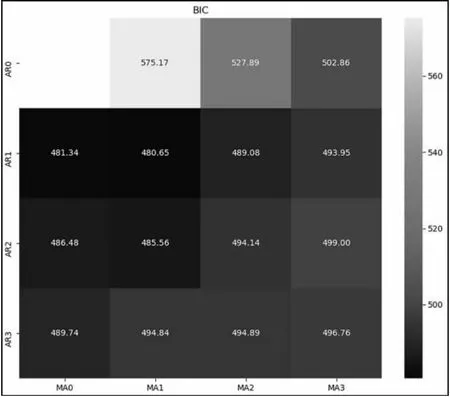
图3 基于BIC准则的AR×MA热力图

通常建立的GARCH模型有四种，其参数设置分别是(1,1)、(1,2)、(2,1)和(2,2)。通过参考AIC准则和BIC准则，使用GS-ARIMA-GARCH组合模型对面料原始序列数据集进行多次不同参数组合的预测试验。最后，通过结果分析可以确定，使用GS-ARIMA(1,0,1)-GARCH(1,1)组合预测模型，且组合模型的参数均达到显著效果，结果如表3所示。

表3 模型参数检验

为了保证GS-ARIMA(1,0,1)-GARCH(1,1)组合模型的预测结果可靠性，需要使用ARCH检验对其残差进行检验分析，从检验结果可以看出F、统计量的P值分别为0.342和0.327，说明组合模型中增加的GARCH模型可以去除面料残差序列中出现的异方差。

3.5 模型诊断

对面料887.601-5730需求量进行预测之前对组合模型先进行模型诊断工作，结果如图4所示，从四个角度对组合模型的效果进行分析探讨。从左上图的标准化残差序列图中可以看出，随着横坐标日期的变化，面料时间序列的残差值没有表现出比较突显的季节性变化，可以暂时认为是由于白噪声的原因而产生的；从右下方的残差自相关图中可以看出，面料时间序列残差和它自己的滞后值之间表现出比较低的相关关系。从右上图的残差直方图和概率密度图中发现，残差概率密度线(KDE)分布曲线和标准正态分布N(0,1)曲线之间几乎重叠在一起，均值也非常接近于0，可以看出组合模型的标准化残差基本可以体现出标准的正态分布。从左下角的残差Q-Q图中可以发现，残差的有序分布几乎贴近于标准正态分布数据采样的线性变化走势。

通过上述模型诊断分析，可采用GS-ARIMA(1,0,1)-GRACH(1,1)模型对面料887.601-5730需求量时间序列进行建模并预测。

图4 模型诊断

3.6 模型预测与评价

运用GS-ARIMA预测模型和GS-ARIMA-GARCH预测模型对2021年1月至2021年10月面料887.601-5730需求量进行预测，其预测结果分别如图5、图6所示。从两个图中可以看出，GS-ARIMA-GARCH预测模型相比GS-ARIMA预测模型，预测值和实际值的波动变化具有较好的一致性，说明取得了良好的预测效果。

图5 GS-ARIMA模型面料原始真实值与预测值比较

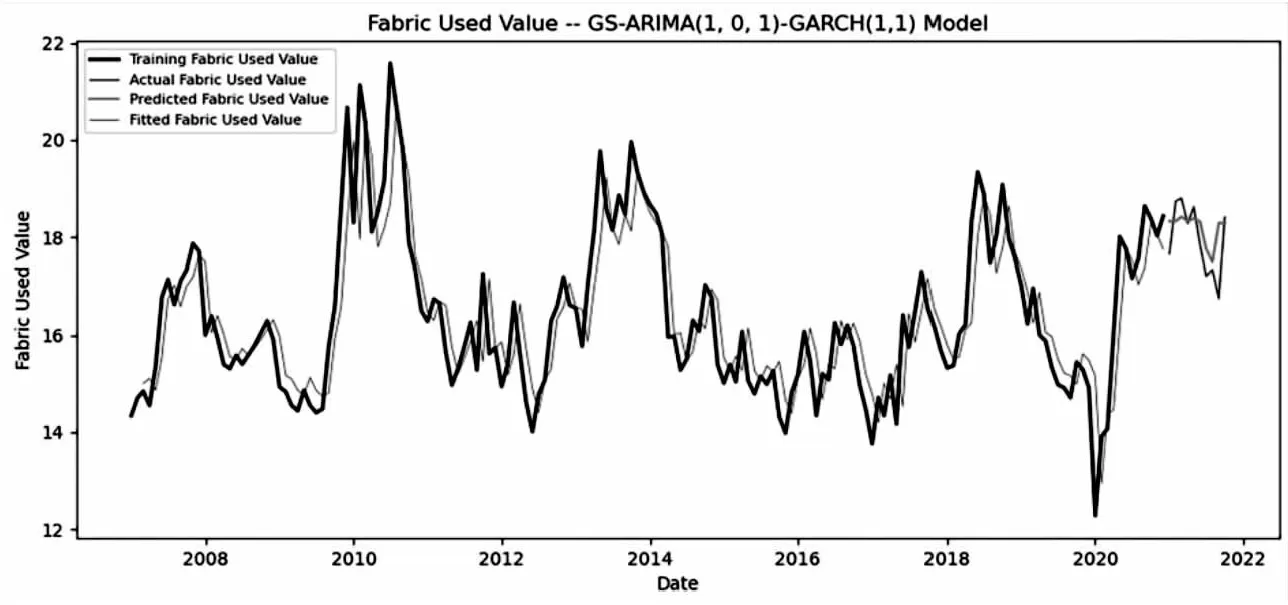
图6 GS-ARIMA-GARCH模型面料原始真实值与预测值比较

将面料原始序列最后10个真实值和组合模型对应的预测结果根据评价指标进行计算、对比分析，最终结果如表4所示。从表4可以看到，在相对误差的计算结果中负值数量较多，同时这个结果也表明组合模型预测值比实际值大一点儿。表中计算的全部相对误差结果大概都是在0.5%～9.0%这个区间内变化，并且计算得到GS-ARIMA-GARCH组合模型的R2值为0.905 504，能够更进一步表明GS-ARIMA-GARCH组合模型预测面料887.601-5730需求量具有较好的准确性。

表4 面料预测值与实际值对比结果

3.7 不同模型精确性比较

为了更加清晰直观地对预测模型的预测效果进行比较，分别计算GS-ARIMA、GS-ARIMA-GARCH预测模型的结果误差，如表5所示。

表5 不同模型精确性比较

从RMSE和MAE计算结果看出，值越小说明其模型预测准确度越高，预测结果越精准。由表5可以看出，GS-ARIMA-GARCH组合模型的预测准确度略胜于GS-ARIMA模型，说明构建的GS-ARIMA-GARCH组合模型对时间序列的预测准确度更高，预测效果更好。也验证了该组合模型具有较好的应用价值，可以投入到服装企业面辅料需求量预测的研究与应用中。

4 结束语

针对服装定制企业面辅料采购和仓库库存利用率问题，构建了面辅料需求量GS-ARIMA-GARCH组合预测模型，以此来提高预测模型的精确度。对组合模型进行平稳性和白噪声检验，说明面料原始时间序列是平稳的时间序列，并且原始残差序列存在异方差的情况。最后，通过对GS-ARIMA预测模型和GS-ARIMA-GARCH预测模型进行精确性对比分析，利用评价指标RMSE值和MAE对其进行判断。从评价指标计算结果可以看出GS-ARIMA-GARCH模型的预测准确精度高于GS-ARIMA模型，预测效果更好。通过实验分析，该预测模型可以帮助企业精准预测近期面辅料需求量，有利于帮助企业人员制定更加合理的面辅料采购计划，从而进一步提升仓库库存的利用率。