非均匀流中E779A螺旋桨空化涡流演变及压力脉动数值分析

何朝晖，龙 云，韩承灶，季 斌

（武汉大学水资源与水电工程科学国家重点实验室，武汉 430072）

0 引言

近年来，我国舰船往大型化和高速化发展，这将导致船用螺旋桨负荷的不断增加，从而产生空化。空化不仅会降低螺旋桨的水力性能，而且会加剧流场的不稳定性，诱导周期性的压力脉动，引起噪声以及空蚀。通过数值模拟方法研究空化对流场的影响对于改善船舶性能有着指导作用。关于空化流动的数值模拟，研究人员最开始研究的是几何形状简单的翼型和回转体，早期螺旋桨的空化流动模拟研究采用势流方法，如升力面方法、面元法等进行求解，随着粘流CFD技术的发展，到20世纪90年代，螺旋桨的空化流动CFD 数值模拟研究逐渐出现并得到快速发展。与势流理论求解不同，粘流CFD 数值模拟方法将粘性的影响加以考虑，能够更为深入地对空化进行描述。Bensow等[1]通过自定义公式近似非均匀来流速度分布，模拟研究了E779A 螺旋桨的非定常空化流动；Shin等[2]基于HEM 方法和蒸汽输运方程，模拟了船后常规及大侧斜螺旋桨周围的空化流动，结果表明非定常空化形态在定性上精度可接受；朱志峰等[3]采用了混合多相流模型，求解了均匀入流工况下的E779A螺旋桨的空化性能，较为准确地预报了片空化；叶金铭等[4]基于空泡混合模型，采用RANS 方法模拟计算了非均匀来流的螺旋桨的空化性能，空泡计算结果与试验较为吻合。近年来尽管数值模拟方法有所改进，但许多研究仍然局限于螺旋桨性能和空化形态的预测。本文以E779A 螺旋桨为研究对象，该桨于意大利船模水池中心经过了详细的敞水性能和空化特性的试验研究。此外，在欧盟相关项目中曾组织多家单位对其均匀来流空化进行了数值模拟比较，拥有较为完整详细的数据。本文重点关注了螺旋桨空化流场的压力脉动及涡量演化，研究了空化对压力脉动以及空化对涡流场的影响。

1 数值模拟方法

本文采用基于求解RANS 方程的方法，结合k-ωSST 湍流模型和Zwart-Gerber-Belamri 空化模型开展螺旋桨空化流动数值模拟研究。

1.1 湍流模型

k-ωSST 湍流模型由Menter 提出，用于改进对逆压梯度流的预测，其能够较好地预测旋转机械周围的空化流动[5]。k-ωSST湍流模型使用混合函数F1将近壁区的k-ω模型与远场的k-ε模型混合。湍流动能k和湍流频率ω的传输方程为

式中参数计算和常数的选取可参考相关文献。

1.2 空化模型

本文采用Zwart-Gerber-Belamri（以下简称ZGB）空化模型[6]来捕捉由空化引起的两相流特征，质量传递用右侧带有两个源项的蒸汽传输方程来处理

单个气泡中的质量变化率与简化的Rayleigh-Plesset方程相结合，以闭合方程(3)，蒸发和冷凝源项最终表示为

式中：ρv代表气体密度，α代表气体体积分数，t代表时间，u代表速度，αnuc代表成核区的体积分数，Rb代表气泡半径，ρl代表液体密度，Fvap和Fcond分别为ZGB空化模型的经验蒸发系数和凝结系数。常用的参数取值有：Rb=1μm，αnuc=5E-4，Fvap=50，Fcond=0.01。

2 几何、网格和边界条件

E779A 螺旋桨为四叶桨，桨模直径为0.227 27 m，其计算域和边界条件见图1。螺旋桨位于旋转域，桨叶表面设置为无滑移壁面。静止部分的外圆柱表面设置为自由滑移壁面。入口边界的非均匀来流速度借助CFX 求解器里的“profile”功能导入试验数据获得，见图2。螺旋桨的转速设置为30.5 r/s。螺旋桨的进速系数为

图1 非均匀来流计算域和边界条件Fig.1 Computational domain and boundary condition of non-uniform inlet flow

图2 数值模拟中的非均匀来流速度分布Fig.2 Non-uniform inflow velocity distribution in the simulation

式中，n为螺旋桨转速，D为螺旋桨直径。

非均匀进口边界与螺旋桨之间的距离设置为0.7D，出口为螺旋桨下游6D处，设置为静压出口，其压力由空化数求得，公式如下：

式中，Pv表示水的饱和蒸汽压力，ρ代表水的密度，pout表示流域出口压力。

通过ANSYS ICEM CFD 软件采用相同的拓扑结构生成了网格数逐渐增大的三套结构化网格，三套网格在x、y、z方向均以 2 倍进行递增，网格总数分别为186万、502万和1404万。选取非均匀来流、进速系数为0.9、空化数为4.455 的空化工况，对E779A 螺旋桨的空化流动进行了数值模拟，使用三套网格计算得到的结果见图3。对于图中选定的三个典型时刻，当网格数量较少时（网格1），数值模拟得到的空化形态与文献[7]中试验结果相比，虽然在变化趋势上是吻合的，但是空化区域的长度和大小均偏小。而随着网格的逐渐细化，预测的空化面积明显增加，与试验结果更加吻合，但当网格细化到一定程度后，改善效果不明显。因此，在保持计算精度的前提下，为了节约计算资源，本文所有的计算选取网格2进行计算。

图3 对比3套网格预测的空化形态Fig.3 Comparison of cavitation patterns predicted by three sets of grids

E779A 螺旋桨及其计算域的结构化网格见图4～5。为了捕获相关位置详细的流场信息，在导边、随边及叶梢区域进行了局部加密。无空化流动的收敛结果被设定为非定常空化流动计算的初始流场。无空化流动残差收敛标准设置为10-5。非定常计算内部迭代的最大次数为每个时间步长20 次，收敛标准采用10-4来平衡时间消耗和计算精度。

图4 E779A螺旋桨结构化网格Fig.4 Structured meshes of the E779A propeller

图5 E779A螺旋桨非均匀来流计算域结构化网格Fig.5 Structured meshes of the fluid domain of non-uniform inlet flow

3 结果与讨论

3.1 非定常空化形态

由于船体几何的干扰，螺旋桨前方水流的来流速度分布往往是不均匀的。为了使数值模拟的结果贴合实际，本文对E779A 螺旋桨在非均匀来流下的空化流动进行了数值模拟，参照文献[7]的计算工况，设置进速系数为0.9，空化数为4.455。由于叶片载荷的周期性变化，在E779A 螺旋桨叶片上观察到空化形态的瞬态变化，见图6，图中展示了E779A 螺旋桨在数值模拟中不同时刻的汽相体积分数为0.1 的等值面图，并与文献[7]中给出的试验得到的空化演变图进行比较。

图6 右图中展示了E779A 螺旋桨在试验中的空化演变图。从图中可以看到：对于选定的桨叶，在旋转角为-25°时，螺旋桨叶背的导边近叶梢处，空化得到初步的形成，并随着角度的增大，空化的体积在逐渐增大；在旋转角为0°时，空化的发展几乎达到最大程度，此时，片空化逐渐卷起进入梢涡，空化开始变得不稳定；在旋转角为10°时，叶片已经开始离开尾流速度较小的区域，空化从下边区域开始收缩溃灭，体积有所减小，并且可以观察到延伸至梢涡区域的空化旋转运动；在旋转角为20°时，空化进一步往叶梢区域收缩，大部分都转变成了不稳定的云空化，梢涡空化得到进一步发展。

图6 E779A螺旋桨非均匀来流工况数值模拟与文献[7]空化形态对比Fig.6 Comparison of the predicted and experimental cavity patterns of E779A propeller of non-uniform inlet flow

从图6 左图中可以看到：对于选定的桨叶，在旋转角为-25°时，空化初步在叶背导边处形成，并随着角度的增大，空化的体积逐步增大；在旋转角为0°时，空化的体积达到最大值，此后，随着角度的增大，空化的体积逐渐向上缩小；在旋转角度为20°时，可以明显观察到梢涡空化的形成。可见，本文对E779A 螺旋桨的非定常模拟结果与试验结果相比，无论在空化的形态还是空化的演变趋势上均有较好的一致性，这表明本文的数值模拟结果是可靠的。

3.2 压力脉动

上文对非定常空化形态的分析，验证了本文非定常空化数值模拟方法的可靠性。为了进一步研究空化的产生对流场的影响，依据试验[8]中的布置，本文选取距离桨毂中心300 mm 的四个监测点对螺旋桨的压力脉动进行了分析，其空间位置见图7。数值模拟得到的螺旋桨模型在无空化与空化条件下，四个不同位置监测点（p1、p2、p3、p4）处的压力脉动，见图8。图中，压力脉动幅值表示为无量纲参数Kp[9]：

图7 E779A螺旋桨压力脉动监测点示意图Fig.7 Sketch of pressure fluctuation monitoring points for E779A propeller

式中，p为监测点压力，ρ为流体密度，Kb为固壁参数，取为2。

图8（a）为无空化工况，四个监测点处的脉动压力频率是相同的，均为螺旋桨的叶片通过频率。脉动压力系数在4.552～4.582的范围内上下波动，波动范围较小。对比四幅曲线图可以看到，四个监测点具有的脉动压力相位是不相同的，这是因为各监测点相对于螺旋桨的几何位置不同。图8（b）为空化工况，脉动压力系数波动范围增大，在4.51～4.61之间。对比四幅图可以看到，空化发生后，不仅四个监测点脉动压力的变化频率同为叶片的通过频率，而且其压力脉动的相位也是一样的。这正是空化条件下的脉动压力变化趋势与无空化条件下的脉动压力变化趋势最明显的区别。

图8 四个监测点上的压力脉动Fig.8 Pressure fluctuations at four monitoring points

计算得到的四个监测点的压力脉动幅值变化曲线，见图9。在无空化工况（图9（a）），四个监测点处的压力脉动主要成分是一阶叶片通过频率分量，脉动幅值均较小，在0.004 以下。而在空化发生后（图9（b）），压力脉动主要成分除了一阶叶片通过频率分量，还有二阶乃至更高阶叶片通过频率分量。通过图9（a）和图9（b）的对比可以明显看到，空化发生后，四个监测点的一阶叶片通过频率分量显著增大，均在0.01以上。而且由于空化的影响，二阶叶片通过频率分量也远比无空化时的一阶叶片通过频率大得多，这表明空化时的压力脉动幅值远强于无空化时的压力脉动幅值。此外，由于螺旋桨的每个桨叶都会经历空化的周期性生长和溃灭的演变过程，这个过程会使流场中诱发大幅度的压力脉动，导致所有监测点处压力脉动的同步增大。因此，一旦船后的螺旋桨上发生了周期性演变的空化，就会引发对船体有害的振动和噪声，从而影响船舶运行的舒适性和安全性。

图9 四个监测点上的压力脉动幅值Fig.9 Amplitude of pressure fluctuation at four monitoring points

为了定量评估非定常空化流动下数值计算得到的压力脉动的结果，将四个监测点的压力脉动幅值的一阶分量与相对应的试验结果[8]进行分析比较，见图10。图中数值结果及试验结果通过公式（8）进行了无量纲化。从图中可以看到，数值模拟的结果均比试验的结果要稍稍偏大，两者的平均误差为8.93%，在p4 点误差最大，为16.89%，但总体来说计算结果与试验结果是较为吻合的。这些结果表明，使用当前的数值方法预测螺旋桨周围场点的压力脉动是可行的。这有助于工程上预防及控制空化引起的压力脉动带来的不利影响。

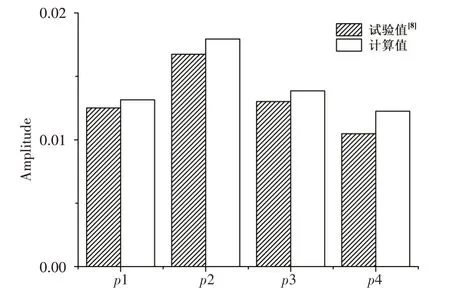
图10 四个监测点压力脉动幅值的一阶叶片通过频率分量的对比Fig.10 Comparison of the first blade passing frequency component of pressure amplitude at four monitoring points

3.3 涡量输运方程

为了进一步研究空化对螺旋桨周围涡流场的影响，采用圆柱坐标系[10]中的相对涡量输运方程进行分析，其表达式如下：

式中，ω是相对涡量，u是相对速度，v是运动粘度，ρ是混合密度，ω1是螺旋桨的旋转速度。

在此方程中，涡量变化率由右侧的五个分量所组成。其中第一项代表相对涡流拉伸，由速度梯度决定；第二项是由于体积变化引起的相对涡流收缩膨胀，这说明了流体可压缩性对涡流的影响；第三项是斜压扭矩项，由压力梯度与密度梯度不平衡而产生，在正压流体中等于零；第四项是粘性扩散项，反映流体相对运动中因粘性而导致的涡量扩散；第五项表明了科氏力在旋转坐标系中对相对涡量的影响。

空化气相体积分数αv=0.1 等值面图、气相体积分数αv=0.1 的云图及上式中涡量输运方程右侧五项周向方向分量的云图见图11。图中沿空化的发展方向选取了6个观察平面，分别位于空化的前部，中部以及尾部。从图中可以看到，涡量场的演变与空化是密切相关的。相对周向涡量拉伸项与其他四项相比明显是较大的，而随着空化的发展，叶尖区域的相对涡量拉伸项呈现出更加复杂的发展趋势，这表明空化的发展会促进拉伸项的发展，从而加剧湍流和涡流的不稳定性。周向相对涡量拉伸项在空化内外的分布呈现正负交错，这表明沿该区域相对较强的涡量输运对旋涡的发展具有促进作用。在螺旋桨的尾流附近，周向相对涡量拉伸项仍然很大，是影响涡量输送的主要因素。此外，与速度散度相关的收缩膨胀项主要集中在空化内部，表明了空化内部流动可压缩性的影响。图中清楚地显示了周向相对涡斜压扭矩项沿汽液交界面是显著的，这是由该处密度梯度和压力梯度不平衡所导致的。在非定常流动中，由空化引起的速度散度和压力、密度梯度不平衡使得收缩膨胀项和斜压扭矩项都是促进涡量产生和改变涡量场的重要源项。而剩余的相对轴向涡粘性耗散项和科氏力项相对于其他三项而言比较小，对涡流场发展的贡献较小。综上所述，空化发生后，引起的涡量拉伸、收缩膨胀及斜压力矩会促进涡的产生和发展，加剧流场的不稳定。

图11 预测的相对涡量拉伸项，膨胀项，斜压扭矩项，粘性扩散项，科氏力项Fig.11 Predicted relative vortex stretching,vortex dilatation,baroclinic torque and Coriolis force terms

4 结 论

本文采用求解基于k-ωSST 湍流模型和Zwart-Gerber-Belamri 空化模型的RANS 方程的方法对E779A螺旋桨的非定常空化流动进行了数值模拟，主要结论如下：

（1）通过对E779A 螺旋桨的非均匀来流空化进行模拟研究，得到的非定常空化无论形态还是演变过程均与试验结果较为吻合，验证了本文计算的可靠性。

（2）对螺旋桨周围无空化及空化压力脉动的对比分析结果表明，空化的发生将会诱发大幅度周期性演变的压力脉动，从而引发对船舶不利的振动和噪声。

（3）对空化流场中相对涡量输运方程各项分量的比较分析结果表明，由空化引起的涡量拉伸、收缩膨胀和斜压力矩是影响涡量场的主要因素，其会促进涡的生成和发展，从而加剧流场的不稳定性。