摆动平板水动力性能的实验与数值研究

周军伟，梅 蕾，郭 斌，李明阳，潘小云

（哈尔滨工业大学（威海）海洋工程学院，山东威海 264209）

0 引 言

自然游泳者诸如鱼类、水生哺乳动物等已经进化得相当完美，其神秘的游动机理带来了低噪声、高机动性和超高效率的游动[1]。近几十年来，越来越多的科研工作者致力于揭开仿生推进的神秘“面纱”，不断解析生物游动中暗藏的物理规律，并逐步应用于工程实践中。从产生推力的水动力特征来划分，仿生推进大致可以分为三类，分别是喷射法，如乌贼等；摆动身体法，如鳗鱼等；摆动翼法，如海龟等。其中，摆动翼法可同时执行平移和旋转运动，形成类似拍打的运动，在拍打过程中，涡流可以被卷起到尾流区域形成反向的von-Karman涡流道，以产生推力[2]。

由于摆动翼法运动形式自由度少，推进效率高，可达80%[3-6]，且便于工程实现，因而研究者们展开了大量的研究，包括自然观察、理论分析、实验研究和计算研究。早期的研究主要通过自然观察进行的[7-9]，研究指出，游泳动物试图维持某些参数以达到最佳效率。为了找出这些参数，已经进行了许多有关摆翼推进的实验和数值模拟研究。Lighthill[1]较早就发展了一种二维摆动翼的线性理论方法。随后，在1995 年Streitlien 等[10]对该方法进行了改进，使其能够计算大摆幅运动情况。而后，Anderson等[3]对比了Lighthill 的线性方法与Streitlien 的非线性方法在求解摆翼问题上的结果差异，并与自己的实验测量结果进行了对比。而Schouveiler 等[4]采用与Anderson 同样的方法进行了摆翼性能的实验测量和数值计算，并对摆翼的工作机理进行了更加深入的研究。从以上研究者的数值与实验的对比研究来看，基于势流理论的数值方法与实验结果存在一定的误差。1996 年，Tuncer 等[11]引入粘流理论，采用求解二维粘流方程的方法得到了一组串列摆翼的性能。而后，Jones 等[12]采用与Tuncer 相同的粘流方程计算方法计算了某摆翼性能，并进行了实验测量。但从结果对比来看，计算结果与实验结果相差仍明显。

为了更准确地模拟摆翼的大摆幅和非定常运动特征，许多新的方法得以发展。Smith 等[13]发展了一种基于弹性网格的RANS求解器，使其能够方便地求解三维摆动翼的水动力性能。Akhtar等[14]发展了一种浸入式边界方法，以适应摆翼的大幅度运动，并对一对串列的摆动平板的性能进行了研究。张曦等[6]以一个鱼尾型的三维摆翼为研究对象，将面元法的计算结果与软件Fluent的计算结果和实验结果进行了对比，结果吻合较好。陈刚等[15]利用浸入边界法和格子Boltzmann 方法来研究几何参数对三维仿生运动摆翼推进性能的影响。Karbasiana 等[16]采用开源CFD 软件OpenForm 的动网格功能实现了二维摆翼的水动力模拟。Mannam 等[17]研究了企鹅模式摆翼的推进性能，并将Fluent 计算结果与实验结果进行了对比，吻合也较好。

出于继续丰富摆翼研究的实验数据和数值方法的目的，本文设计了一种简易的两自由度摆翼试验平台，实现了预定的两自由度运动轨迹，并在循环水槽开展了摆动平板推进性能实验研究；随后基于动网格技术，利用流体数值仿真软件对摆动平板推进性能进行了数值仿真分析，并与实验结果进行了对比分析。最后，针对实验中摆动平板效率较低的情况，数值分析了平板前后缘导圆、无限展长假设和大摆幅对效率的影响，以期待可以进一步地对试验平台进行改进。

1 摆翼实验平台设计

1.1 摆翼运动机理

简单的摆翼运动可描述为匀速前进（X方向平移）、横荡（Y方向平移）和首摇（绕Z轴旋转）三自由度耦合运动。摆翼运动使用绝对坐标系xoy，其运动模式如图1所示。图中以某翼型代替本研究中的平板，VA为摆翼的恒定前进速度，T为摆动周期，B为摆动幅度，即扫掠宽度。其中，横荡运动和首摇均为正弦规律的运动，横荡位移Y和首摇角度θ分别表示为

图1 摆翼运动和受力示意图Fig.1 Schematic diagram of flapping foil motion and force

式中，Y0是横荡幅度（m），θ0是首摇幅度（rad），f是频率（Hz），φ是横荡运动和首摇运动之间的相位差（rad），t是时间（s）。

1.2 性能参数定义

对比螺旋桨的进速系数定义，本文选用横荡扫掠宽度B作为特征长度，定义进程hp与横荡扫掠宽度B的比值为进速系数，以J表示：

由式（3）可知，在频率f、扫掠宽度B一定的条件下，改变VA值即可得到不同的进速系数J，本文摆翼运动的不同工况即指不同进速系数的工况。许多文献中，采用斯特劳哈尔数St代替进速系数来描述摆翼的不同工况，两者关系表示为

参照螺旋桨性能推力系数的定义以及Floc’h等[5]的定义方法，以摆翼扫掠面积BH为参考面积，以fB为参考速度，其中H为摆翼的展长，重新定义推力系数KT为

按相对速度计算，摆翼推进器的工作Re数可表示为

式中，ν为水的运动粘度系数。本文各工况雷诺数Re约在1.6 × 105～5.0 × 105的范围内。

1.3 摆翼实验平台整体设计

由于摆翼的运动为三自由度耦合运动，一些研究者采用多个伺服电机来实现上述结构[3-4,18], 但本文实验中发现该结构的脉动力明显，为了减轻脉动，实现摆翼连续平滑的运动，并简化试验机构，本设计参照刘江鹓等的工作[19]，采用曲柄连杆结构和直流电机相结合的方式控制摆翼运动，如图2 所示。本文采用曲柄连杆滑轨机构来实现往复的横荡运动，采用第二套曲柄连杆滑轨来控制以实现一定的摆角θ。其中两滑块分别连接以同转速异相位圆周运动的曲柄，以保证θ值呈近似正弦变化规律，两曲柄间的相位差可控制θ的幅值大小，且可以保证横荡和首摇运动间的相位差φ为90°。水平摆幅的大小可通过调整曲柄长度实现。图2中红色铰链绕X轴旋转，蓝色铰链绕Z轴旋转。

图2 摆翼机构运动原理示意图Fig.2 Schematic diagram of motion principle of flapping foil mechanism

如图3实物图和装配图所示，摆翼机构共分为四大部分：电机驱动部分、曲柄连杆部分、滑块轨道部分和摆翼测量部分。电机驱动部分为整套装置提供动力并通过联轴器将电机与曲柄轴相连接，带动曲柄做圆周运动；两曲柄间也与联轴器固接，以实现同转速转动；曲柄连杆带动滑块做水平运动；滑块与摆翼通过铰链链接，带动摆翼作预定轨迹运动；测力装置固连在摆翼上方，这里设计采用三分力天平测量摆翼受力。试验中用平板代替摆翼，弦长c=0.1 m，竖直浸入水中，浸没展长H=0.45 m。平板截面为矩形，厚度为5 mm，即弦长厚度比为20。平板实验件与自制三分力天平如图4所示。

图3 曲柄连杆滑轨机构的实物图和示意图Fig.3 Picture（left）and schematic diagram（right）of crank connecting rod slide rail mechanism

图4 平板实验件（左）与自制三分力测力计（右）Fig.4 Plate test specimen（left）and self-made three axis force sensor（right）

由于曲柄连杆方式不能得到标准的正弦曲线，因而必须通过各部分的几何关系计算出摆翼运动中每一时刻的首摇角θ（t）和水平位置Y（t）。换算方法为：由摆翼曲柄的转动方程，结合曲柄长度和连杆长度推出其中一曲柄控制的滑块水平位置时变曲线，进而通过两曲柄间的相位差可求出另一滑块的水平位置时变曲线，两水平位置中心便是摆翼的型心位置；通过两个滑块的位置、摆翼的弦长和铰链的长度即可求得首摇角度θ（t）。具体的换算和推导过程详见附录A。设计电机转速为1 r/s，实际实验中测得电机转速为1.011 r/s，即摆动频率f=1.011 Hz，周期约为T=0.989 s。两组曲柄设计长度均为80 mm，连杆长度都为200 mm，当驱动电机匀速转动，可得A点的横荡运动曲线y，如图5（a）所示，横荡幅度为Y0=80 mm。图2 中黑色L 型支架的长边S1为148 mm，短边S2为80 mm。定义两个曲柄间相位差为Δβ，当Δβ分别取0.4 rad 和0.6 rad 时，可得平板的首摇运动曲线θ（t），如图5（b）所示，首摇摆角幅度分别约为0.23 rad和0.35 rad。从图中可以明显看出，两个运动的曲线都不是简谐的，即两个运动的规律均未达到绝对的正弦曲线形式。由理论分析可知，增加连杆长度和S2长度可以改善这一现象，但为了减小装置的整体尺寸，本文中并未尝试。

图5 摆动平板的横荡运动曲线和两个不同相位差下的首摇运动曲线Fig.5 Heave motion and pitching angles under two different phase differences of flapping plate

1.4 测量和数据采集

实验采用三分力天平作为测力计测量推力Fx、侧向力Fy以及扭矩Mz，测力计固连在图2中S1支架的中点位置，同时与平板固连，其示意图如图3（b）所示。当平板运动时，实验测量的力的矢量方向是随时间变化的，因而实验中实测的力为沿平板弦向的力Fs、垂直平板方向的力Fn，以及绕Z轴的转矩Mz，坐标系如图2 所示，Fs、Fn与Fx、Fy的关系如图6 所示。已知测得的Fs和Fn，根据如下关系可得出Fx和Fy：

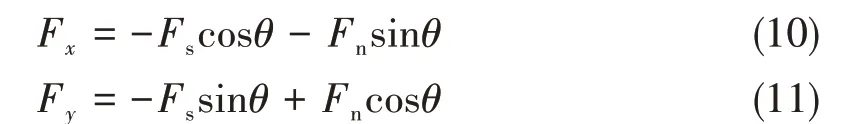
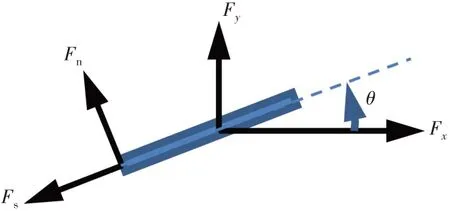
图6 平板受力示意图Fig.6 Sketch of forces on flapping foil

实验装置在循环水槽中对摆动平板的受力进行测量，测量段长8 m，宽2 m，深1.2 m。摆动平板竖直浸入水中，通过控制来流速度VA实现不同工况的测量。采用东华DH5908 无线动态应变采集器进行数据采集，采样频率为200 Hz，即采样周期为0.005 s。为了去除测量结果中的杂波，采用FFT 低通滤波对测量数据进行处理。考虑测量信号中主要关注的是低频分量，且实验用循环水槽动力设备振动频率为3～6 Hz，因而本文中截止频率选用2.5 Hz，以消除设备振动对测量结果的影响。图7 列出了两个分别代表杂波较小（Fn的应变测量数据）和杂波较大（Fs的应变测量数据）的滤波情况，图中工况都为Δβ=0.6 rad，来流速度为0.6 m/s，黑线为原始测量数据，红线为滤波后数据。从滤波结果来看，图7（b）中Fn应变测量数据在滤波前后趋势几乎一致，仅滤掉了较小幅度的杂波；图7（a）中Fs的应变结果相差较大，部分幅度明显的高频被滤掉了，但考虑到高频分量对摆动平板的时均性能影响较小，因而本文采用2.5 Hz的低通滤波截止频率是可行的。

图7 Δβ=0.6 rad，VA=0.6 m/s工况下弦向应变与法向应变的测量数据及滤波结果Fig.7 Measured data and filtering results of tangential strain and normal strain under Δβ=0.6 rad，VA=0.6 m/s working condition

2 摆翼推进性能数值分析

本文采用NUMECA 公司的CFD 软件包FINE/Marine 求解摆翼平板周围流场。该软件采用动网格技术实现对运动物体周围流场的模拟，采用高分辨率格式能够很好地捕捉到自由液面，能够满足摆翼大幅度运动的流场的模拟要求。

2.1 控制方程

求解积分型不可压粘性流体动力学方程，考虑网格单元的运动和重力的影响，连续方程和动量方程分别为

式中：Ω表示单元体积；Sj表示单元面积矢量S的各个分量；vi表示速度矢量v的各个分速度；τij为粘性应力张量的各个分量；p为压强；gi为单元的加速度分量，其仅在重力方向有分量，大小为重力加速度g。算例采用的湍流模型均为k-ω（SST）模型，湍流模型的具体参数参见Menter[20]的工作，该模型考虑了湍流切应力传递的影响，在逆压梯度和分离流中表现优异。

2.2 网格划分及无关性验证

2.2.1 网格划分

利用NUMECA 系列软件中的HEXPRESS 模块生成矩形体网格，逐次进行网格加密。首先在平板表面进行网格加密，使最大网格尺度小于1/64 弦长；在翼型尾流区域进行两次网格加密，以保证尾涡的较精确模拟，其中在2c×10c×h的区域（加密区1），最大网格尺寸小于1/16弦长，在10c×20c×h的区域（加密区2），最大网格尺寸小于1/4 弦长，h为平板高度；在自由液面附近亦进行了网格加密。整个计算域大小约为25c×25c×50c，网格剖视如图8 所示。计算中采用网格刚性平移+弹性扭曲的策略，以适应平板的大幅度运动。在本文中，平板仅在Z轴方向发生一定角度的偏转，随平板偏转而发生变形的网格示例如图9所示。

图8 网格剖示图Fig.8 Schematic diagram of grid section

图9 水下0.2米处平板在发生首摇时网格所发生的局部形变示例Fig.9 Example of grid local deformation in case of pitching motion of foil at 0.2 m under water

2.2.2 边界条件

算例边界条件如图10 所示，摆翼壁面为无滑移壁面条件，摆翼前方为远场来流条件（来流速度为进速VA，压强为当地静压），左、右侧和后方均为零压梯度条件（第二类Neumann边界条件，即∂p/∂n=0，速度为远场来流速度），上方和下方为描述压力条件（第一类Dirichlet 边界条件，压强为给定当地静压，速度为远场来流速度），V→mir×n→=0。

图10 边界条件示意图Fig.10 Schematic diagram of boundary condition

2.2.3 网格无关性验证根据课题组前期研究结果，摆翼尾流区域的网格大小对性能曲线影响较小，摆翼周围网格大小对性能曲线的影响远低于壁面网格大小，可在资源充沛时适当加密。因此本文中验证网格的无关性时仅对比了平板壁面三种加密形式对性能的影响。网格细分方法如表1所示，三种网格计算得到的效率结果如图11所示。验证工作的首摇幅度均取为0.23 rad，湍流模型选用的是k-ω模型，时间步长为0.002 s。由图11可知，网格1和网格2效率曲线差距较大，即棱边加密对摆动平板效率的影响较明显；而网格2与网格3 的效率曲线几乎重合，即继续细分平板表面网格对效率几乎没有影响。因此后文中将选用网格2来展开讨论。

图11 三种网格对效率的影响Fig.11 Performance curves of three different mesh sizes

表1 网格划分情况Tab.1 Details of mesh refinement

2.3 数值方法验证

为验证文中数值方法在模拟摆翼推进方面的可靠性，本文与Anderson 等[3]、Read 等[21]和Schou⁃veiler 等[4]实验中的工况进行了同工况模拟验证，具体参数可参照相应的文献。效率和推力系数的结果对比如图12所示，从对比结果来看，本文计算结果与三个文献中的实验结果均比较吻合。图12（b）中的cT为Anderson等[3]定义的推力系数，详见文献[13]。同时针对Schouveiler等[4]观测的NACA 0012翼型的摆翼进行了同工况数值模拟，摆翼为展弦比6、两端相对壁面滑动的准二维平直翼，上下摆幅Y0=0.075 m，摆动频率f=1.2 Hz，St=0.45，最大攻角为20°，观测位置为中间截面，其对比如图13 所示。图13（a）和图13（b）中分别显示了翼型中间截面的尾涡实验观测图和模拟云图，可以看出模拟结果和实验结果的尾涡形状非常接近。综上，可以证明本文对摆翼性能的计算方法较为可靠。

图12 文献与本文仿真数据的对比验证（红色曲线为本文工作，●为Anderson实验结果，▲为Read实验结果，▽为Schouveiler实验结果。）Fig.12 Comparison of simulation results with previous computational and experimental results

图13 St=0.45，amax=20°工况下文献试验结果与本文数值结果的尾涡对比图Fig.13 Comparison of vorticity patterns visualized in the foil wake for St=0.45,amax=20°between the experimental results of Schouveiler et al[4]and the numerical results in this paper

3 试验与模拟结果对比分析

本文装置在哈尔滨工业大学（威海）的循环水池完成了相关实验，试验和数值模拟均在摆动频率f=1.011 Hz，相位差φ=90º，升沉幅度Y0=80 mm 的工况下进行。在曲柄相位差设定分别为Δβ=0.6 rad 和Δβ=0.4 rad，摆角幅度分别约为0.23 rad和0.35 rad时，在VA=0.2 m/s、0.4 m/s、0.6 m/s和0.8 m/s四个来流速度下进行测量，得到摆动平板实际Fx、Fy和Mz。

3.1 性能和受力分析

图14 给出了曲柄相位差分别为Δβ=0.6 rad 和Δβ=0.4 rad 两个首摇运动曲线下效率和推力系数的实验和数值模拟结果对比。从整体来看两者趋势一致，但实验测得的效率和推力系数均略低于数值计算结果，推力系数的最左侧点除外，曲柄相位差Δβ=0.6 rad 情况下的效率要比Δβ=0.4 rad 情况下更高一些。从图14（a）可知，曲柄相位差的增加，即摆角的增加会在低进速系数下获得较高的效率，但同时随着进速系数的增加，效率下降较快。而小摆角摆翼却能在较宽的进速系数下保持较高的效率，即小摆角摆翼的工作范围较宽，这与课题组之前的研究结果相一致[22]。从图14（b）可以发现，整体来看两种不同曲柄相位差的推力系数KT差别不大，即首摇摆角幅度对推力系数影响不大，这是由于推力Fx在这两组工况中变化很小，这可以从后面图15的推力曲线时程图对比得出；而在低进速系数，曲柄相位差Δβ=0.6 rad 的工况下推力系数KT较曲柄相位差Δβ=0.4 rad 的工况略大，但随着进速系数的增加，曲柄相位差较大的工况推力系数下降较快，这与图14（a）中大摆角摆翼效率下降较快相一致。

图14 推进效率和推力系数的实验结果与数值模拟结果的对比Fig.14 Comparison between experimental results and numerical simulation results of propulsion efficiency and thrust coefficient

为了详细分析实验结果与数值计算结果之间差异的原因，本节进一步对比了各工况下的实验测试和数值模拟结果的推力时程曲线、侧向力时程曲线和转矩时程曲线，如图15所示。首先，较普遍的现象是，与Fx和Mz相比，Fy的实验测量结果与数值计算结果更吻合一些。由公式（11）和公式（12）可知，Fx的结果在很大程度上依赖Fs，而Fy的结果更依赖Fn，而从图7中Fs和Fn的测量结果可以看出，弦向力Fs脉动十分剧烈且杂波较多，可靠性较低，这可能是测试系统受到循环水槽振动干扰引起的；而法向力Fn测试结果较为稳定，且干扰较少，所以由其确定的Fy的实验测量结果与数值计算结果更吻合一些。其次从横向和纵向对比的结果来看，当曲柄相位差Δβ固定，即摆角固定时，随着进速VA从0.2 m/s增加到0.8 m/s，试验和数值模拟的推力Fx和侧向力Fy的峰值变化很小，而转矩Mz的峰值随着进速的增大略有增加，约由0.3 N∙m增加到0.4 N∙m；而当进速固定，曲柄相位差Δβ由0.4 rad增加到0.6 rad时可以发现，推力Fx峰值几乎不变，而侧向力Fy和转矩Mz的峰值均有所下降。例如进速VA=0.2 m/s，曲柄相位差分别为0.4 rad 和0.6 rad 的图15（a）和15（e）相比，侧向力Fy从20 N 下降到15 N，而转矩Mz从0.28 N∙m下降到0.2 N∙m，而推力Fx几乎不变，约等于5 N。从效率的公式（8）可知，当与输出功率相关的推力Fx基本不变而与输入功率相关的侧向力Fy和转矩Mz均有所下降时，效率必然增加，这正与前面图14（a）中两个工况效率曲线的对比结果相一致。最后，图中还发现无论在试验结果还是CFD模拟结果中，推力Fx峰值均呈现大小交替的周期变化，而且在试验测试结果中更明显，这是由于摆翼实验装置的首摇和横荡两个运动的曲线都未达到绝对的正弦曲线形式所造成的。而侧向力Fy和转矩Mz的波形偏宽，也明显呈不对称状态，是多个波形的组合，也是上述原因所造成。

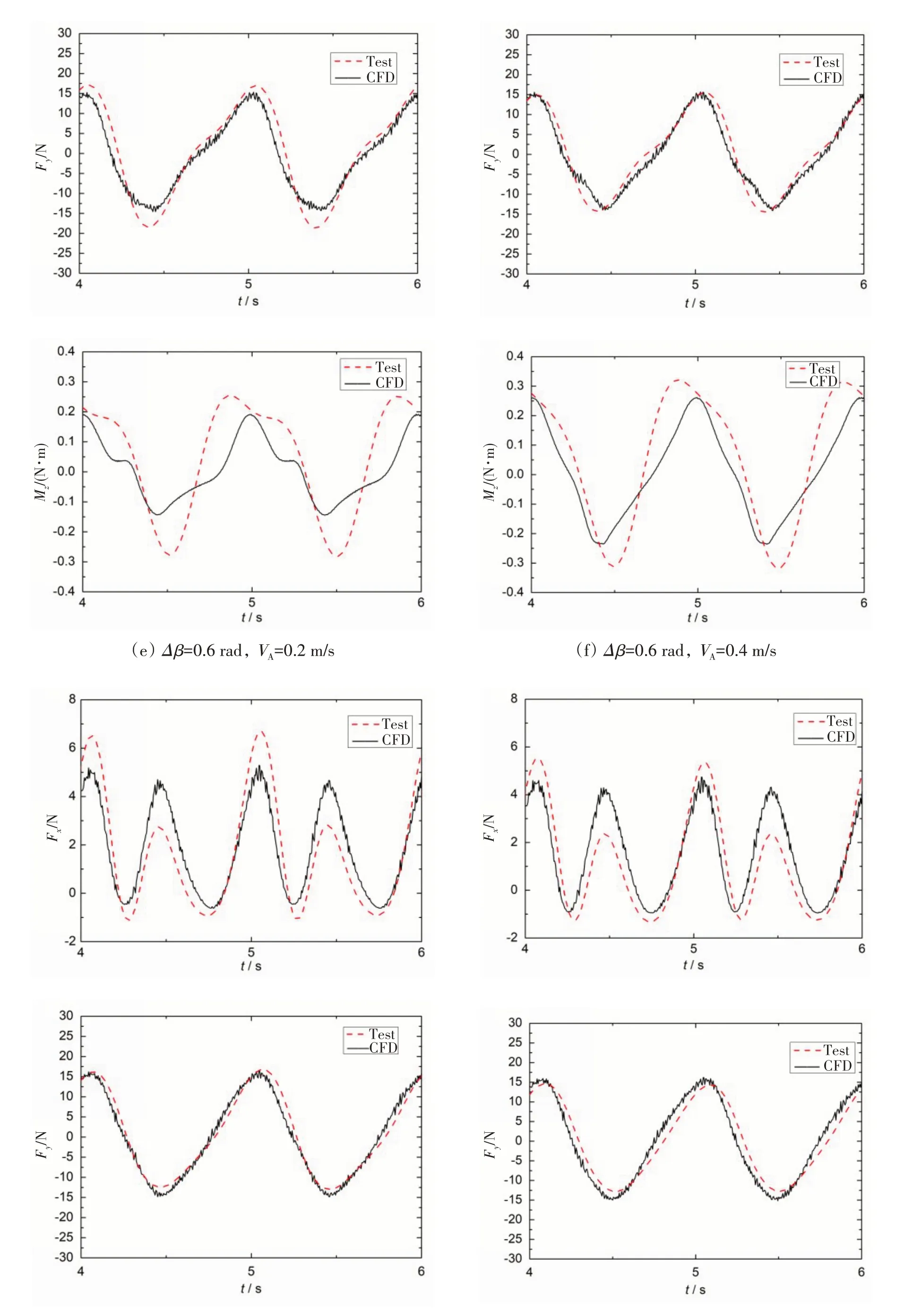
图15 不同曲柄相位差和流速下，Fx、Fy和Mz随时间的变化曲线Fig.15 Curves of Fx,Fy and Mz with time under different crank phase differences and flow velocities

3.2 效率分析

从图14 的实验结果可知，实验测得的最高效率仅有27%，远低于同类型文献中的数据。为了探索效率较低的问题，在摆角轨迹Δβ=0.4 rad的工况下，本节对平板前后缘增加导圆、无限展长假设和大摆幅情况三方面进行简单探讨，设置了4种工况进行数值计算对比：

工况1：矩形截面平板，升沉幅度Y0=80 mm；

工况2：矩形截面平板前后增加倒圆，倒圆半径为1/2 板厚，即2.5 mm，其他计算参数同工况1，网格细节见图16；

图16 工况1和工况2下的网格细节Fig.16 Grid generation under case 1 and case 2

工况3：采用无限展长假设，分析平板底端和自由液面对水动力性能的影响。导圆平板为研究对象，其他技术参数同工况1；

工况4：将平板的横荡和首摇运动都改为简谐规律，其中摆角幅度不变，横荡幅度从80 mm增加至200 mm。采用工况3的计算模型。

4 种工况的数值模拟效率曲线对比如图17 所示。首先可以发现，工况2 的最高效率点在50%左右，与工况1 相比提高约20%。这说明矩形截面平板前后缘的导圆处理能够非常明显地提高推进效率。从表2计算结果可知，相比于工况1，推力Fx在工况2中明显提高，由1.558 N 增大到2.491 N，增大约60%；而与此同时，工况2 中的功率P略有下降，由5.692 W 降低到4.809 W。根据公式（7）可知，工况2 推进效率η必然会增大。从图18 的对比云图中也可以看出，平板摆翼前后缘的倒圆处理可以明显减小分离，进而可以降低阻力。其次，由图17的效率对比可以看出，无限长假设下的工况3与工况2相比，效率提高幅度约10%左右。从图19 工况2 的平板摆翼自由液面处的波高云图可以看出，自由液面处有明显兴波，造成了阻力的增加，而考虑摆动平板的下端面，有限展长的三维摆翼前进的过程中会在翼尖处形成一个拖拽的旋涡，升力下降的同时产生诱导阻力，进而影响效率[21-22]。这也与本课题组前期的研究结果相一致，即较大展弦比的摆翼推进效率更接近无限长假设的理想二维摆翼，而随着展弦比的降低，效率会降低。最后，相比于工况3，工况4 也有约10%的效率提高，其最高效率达到了70.7%。这个效率的提高一方面是由于摆幅比的增大对效率的贡献，另一方面也有对工况1 中摆翼非简谐运动规律的修正对效率的影响，这与Read 等[21]和Hover 等[23]的相关研究结论是一致的。

图17 4种工况下的效率对比Fig.17 Efficiency comparison under four working conditions

表2 工况1和工况2数值计算结果对比Tab.2 Numerical results of Case 1 and Case 2

图18 平板摆翼倒圆前后的尾涡变化Fig.18 Variation of wake vortices before and after rounding of the flapping plate

图19 自由液面处的尾流场Fig.19 Wake field at free surface

3.3 功率分析

摆翼的推进效率为输出功率与输入功率之比。根据公式（7）和公式（8）可知，影响效率值的计算参数不仅包括机械参数Fx、Fy和Mz，还包括速度参数vy和ωz。当摆翼工作时，这些参数随时间而波动，参数之间的相位差对效率结果影响很大。

本文选取了3个代表性的工况点，在图20中对比了其实验与数值结果的Fy-vy和Mz-ωz相图。3个工况分别为：实验测得的最高效率点（Δβ=0.6 rad，VA=0.6 m/s）；最高效率点摆动规律下的较小进速工况（Δβ=0.6 rad，VA=0.2 m/s）；另一个摆动规律下的较大进速工况（Δβ=0.4 rad，VA=0.8 m/s）。从整体上看，无论是实验结果还是数值计算结果，Fy-vy和Mz-ωz都存在一定的相位差，Fy和vy的相位差很小，而Mz和ωz的相位差较大，接近90°。同时，Mz与ωz峰值相乘的结果比Fy与vy峰值相乘的结果小得多，有数量级上的差别。综合以上两点说明y向力Fy在输入功率中产生的功率更大，而绕Z轴的转矩Mz几乎没有做功。

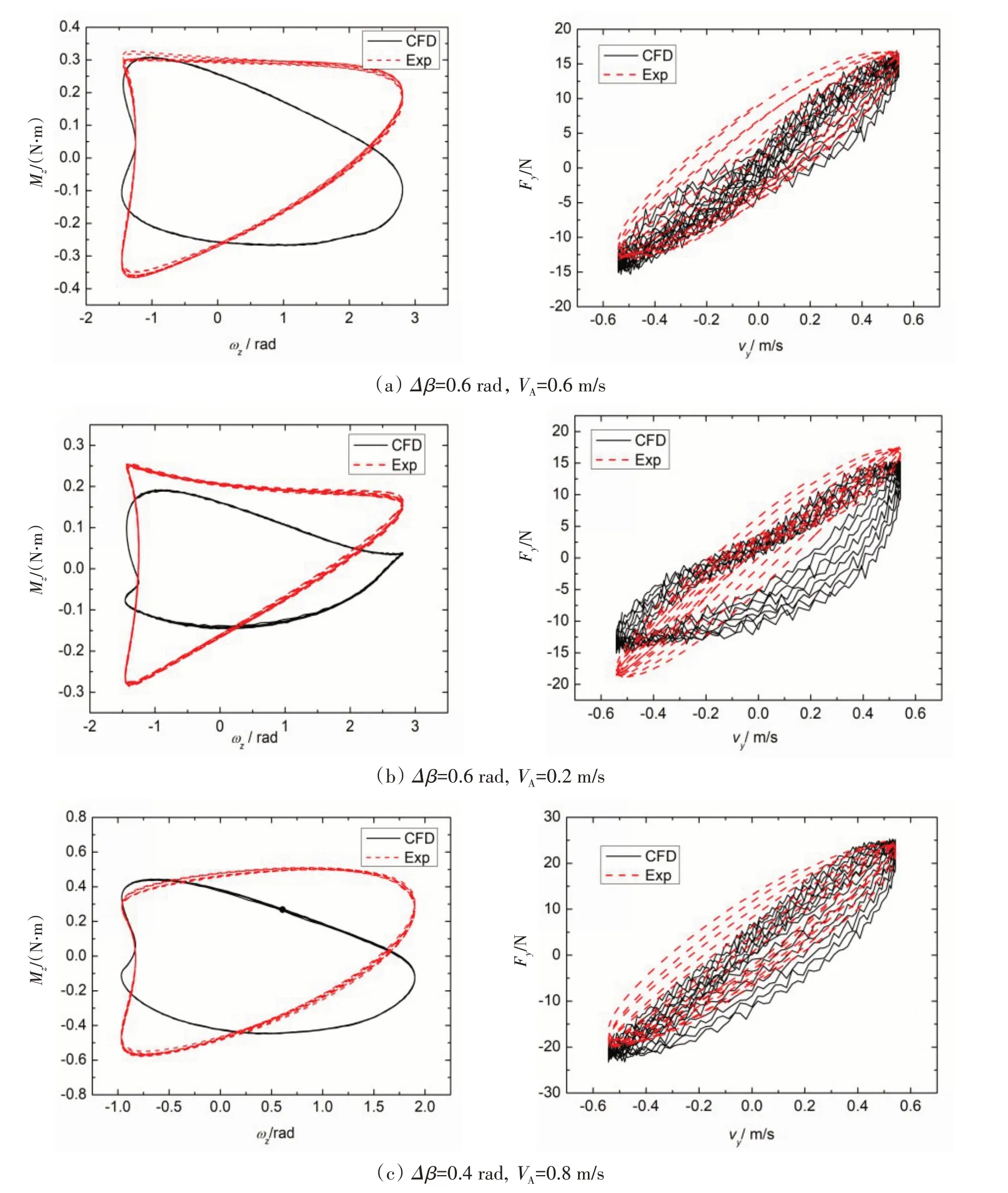
图20 3个工况下的Fy-vy图和Mz-ωz图Fig.20 Phase diagrams of Fy-vy and Mz-ωz at 3 working points

4 结 论

本文设计了一种简易的两自由度摆翼试验平台，并在循环水槽开展了摆翼推进性能实验研究，随后对摆翼推进性能进行了数值仿真分析，并与实验结果进行了对比分析。最后，针对实验中摆翼效率较低的情况，数值分析了平板前后缘导圆、无限展长假设和大摆幅对效率的影响，主要结论如下：

（1）本文设计了一套利用曲柄连杆滑块机构实现摆翼推进的实验装置，并测量了摆动平板在不同来流速度和首摇幅度下的水动力性能。同时，对实验工况进行了数值模拟，以便于对比研究；

（2）同时对实验测量与数值分析的总体性能和各个分力进行了对比。从对比结果来看，实验结果与数值结果之间略有偏差，实验测得的效率和推力系数普遍要略低于数值计算结果。从力的对比来看，法向力Fn吻合较好，弦向力Fs和转矩Mz稍差；

（3）为了分析摆动平板效率较低的原因，设计了另外3 个工况，通过数值模拟得到了与实验工况下效率计算结果的对比。从对比结果来看，平板前后缘导圆、消除端壁和自由液面的影响和增大摆幅都能明显地提高摆动平板的效率；

（4）对摆动平板的输入功率分量进行了分析，从结果来看，在摆动平板的工作过程中，Mz几乎不做功，所有输入功率近乎由Fy提供。

附录A：横荡运动与首摇运动的表达式推导过程

根据正文中图2，通过给定A点和B点的位移曲线，计算平板中点的横荡运动位移曲线，及其首摇运动的摆角曲线。B点相对A点延后Δβ相位，并且相对位置右偏LBC长度。根据图中坐标，在曲柄连杆工作平面内（YZ平面），可得两点的运动曲线分别为

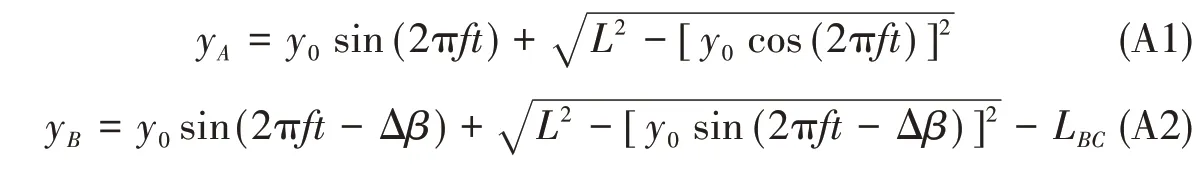
式中，y0为曲柄长度，L为连杆长度，其他变量见论文正文。

两滑轨间距为S1=LAC，则在XY平面内，可得C点的运动曲线。首先计算距离LAB

则摆翼中点坐标为

文中取y在其平均值上下波动。此外，摆翼中点的X坐标也会有微小的波动，本文中对此忽略不计。