简化护卫舰的尾流场优化研究

李 通，王逸斌，赵 宁，邓思强

（1.中国船舶集团有限公司系统工程研究院，北京 100094；2.南京航空航天大学非定常空气动力学与流动控制工业和信息化部重点实验室，南京 210016）

0 引 言

舰船甲板是舰载机在海上作业的主要场地，而甲板上的流场比较复杂，当舰船运动或者有风时，上层建筑后方会产生不均匀的尾流场，常伴随有分离、回流、旋涡等运动形式的发生。特别是对于护卫舰/驱逐舰，其飞行甲板位于机库后方，如图1所示，流动受机库和上层建筑阻挡，在背风处形成涡流区，且甲板区域较小，增加了舰载机起降的危险性，所以必须对舰船飞行甲板上方的空气流场特性有一个清楚的认识。早期在研究舰船甲板上方尾流场时主要采用实船测量和风洞试验[1-4]，但是这两种方法需要耗费巨大的人力、物力和时间成本，不能很好地满足现代舰船研究的要求。随着近年来计算机技术的迅猛发展，计算流体力学（CFD）数值模拟手段得到了逐步完善与发展，并在国内外被广泛应用到舰船上方空气流场的研究中[5-11]。Watson 等[12]在2019 年对英国双舰岛航母“伊丽莎白女王号”（HMS Queen Elizabeth）上的非定常气流进行了数值计算和实验建模研究，发现缩比模型试验与全尺寸CFD 计算的结果显示了合理的一致性。同年赵瑞等[13]对国内外舰面流场特性研究进展进行了综述，分别从实船测量、风洞实验以及数值仿真三方面对其关键技术展开讨论。为了建立一个舰船尾流验证数据库，国外提供了高度简化的护卫舰外形（SFS）几何结构模型[14]，图2给出了SFS以及它的更新版本SFS2，在原始SFS 的基础上加长机库并增加三角形舰艏。为了验证SFS/SFS2 预测真实护卫舰飞行甲板上方流场的可靠性，许多学者利用不同的计算方法对SFS/SFS2 的舰面流场进行了一系列的数值模拟研究[15-23]，发现机库后方存在回流区，同时产生了不稳定的分离剪切层。如果直升机在起降过程中陷入回流区，旋翼气动力会受到涡流的扰动，可能会导致飞行事故。

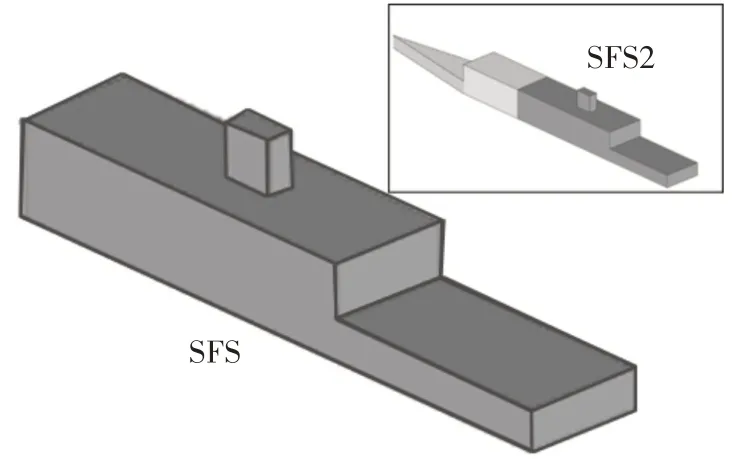
图2 SFS和SFS2几何模型示意图Fig.2 Schematic of SFS/SFS2 model

因此，国内外又有许多学者使用流动控制手段对护卫舰舰面流场进行改善[24-33]，以达到优化舰船尾流场的目的，其中大多数采用被动流动控制手段，主要通过改变机库/上层建筑外形和增加控制装置两种方式。早在2001 年，Tai[24]通过在SFS 前端添加一个圆形舰艏，提出了一种改进的SFS 几何结构。这种改进避免了与船体表面的完全流分离。然而，这种修改并没有改善飞行甲板上的流动特性。后来Shukla等[25]在此基础上采用了圆形舰首和圆形机库门，得到两种几何修改模型，一种是圆形机库门（RH），另一种是圆形机库门和圆形舰首的组合（RH&N），结果显示RH&N模型更好地改善了机库后方起降区的复杂流场。Bardera-Mora 和Meseguer 在风洞中研究了三种不同机库外形的SFS2 模型结构，表明圆形倒角的机库能够有效减小机库后面的回流区[26]。荣吉利等[30]在2019 年采用DES 方法研究三种不同机库外形在0°与右舷45°风向角下对舰船艉部大分离流场的影响。结果表明，相比两侧较低高度的机库外形，等高外形的机库不利于直升机的舰面安全起降，通过合理的降低机库高度可以有效地改善艉部飞行甲板处的起降环境。对于增加控制装置的方式，可以分为两类：导流型和过滤型[31]。导流型（如斜板）是为了将不期望的流动输送到不重要的区域，过滤型（如多孔屏）是为了减小流动的不稳定性。Greenwell 和Barrett 等[32]在试验中给SFS 机库门周围安装一些倾斜的多孔屏，通过减小湍流度和垂向速度来改善飞行甲板上的气流。他们发现，安装在机库侧面和顶部并向后倾斜的密集屏具有最佳性能。2019 年陈华健等[33]开展了舰船流动控制对直升机着舰域流场的影响研究，结果表明在无侧风情况下，安装舰岛斜板和锯形挡板控制装置能够有效降低着舰域气流分离和涡的能量等级。

对于以往的舰面流场优化研究，被动控制手段由于简单且成本低，被大多数学者所青睐，但主要是通过对比几种不同舰船结构下的流动参数来选定最终的优化结构，而无论是改变外形还是增加装置，往往会涉及到多个参数，比如机库的长宽高或斜板的长宽以及倾斜角度，这些参数的取值较多，如果只取个别参数进行几个模型之间的对比，则无法找到准确的最优模型，如果选取较多参数形成大量模型，则会大大增加数值计算或者实验的成本，也有可能这些参数都没有对应最优模型。为了解决这一问题，本文结合CFD 方法和人工神经网络方法，针对护卫舰后体简化模型，通过改变机库的长度和宽度，对机库后方回流区的大小建立两种不同的神经网络预测模型，得到基于长度和宽度的响应面，最后使用粒子群优化方法找到最小回流区对应的机库长度和宽度，对舰船设计具有一定的参考价值。

1 研究方法

1.1 数值计算方法

由于舰船甲板上方的流动为低速不可压流动，所以给出不可压流动的控制方程：

上述方程中式（1）为连续方程，其中V为速度矢量；式（2）为动量方程，其中D/Dt为物质导数，描述运动流体微团的某个量随时间的变化率，ρ为流体的密度，P为流体所受的压强大小，F为粘性力矢量。使用Fluent 对流场进行数值计算，采用雷诺平均方法中的k-ε湍流模型来封闭方程，选择基于压力的SIMPLE（Semi-Implicit Method for Pressure-Linked Equation）算法计算。

1.2 数值方法验证

本文首先对SFS2模型周围的流场进行了数值计算，并将其结果与实验数据和其他学者的计算结果进行了比较[11，20]。其中实验是在加拿大国家研究委员会（NRC）的空气动力实验室中2 m×3 m 的风洞中进行的，使用1:100的SFS2 缩比模型，以下给出了0°风向角、40 kn 来流风速下的实验数据。在SFS2 甲板上方取一横向观测线，该观测线平行于甲板表面，长度为甲板宽度的两倍，其在垂直方向上的投影位于甲板中心，如图3中红线所示。图4给出了在实验和数值计算下，观测线上的速度分布曲线的对比，其中y表示观测线上的点到甲板中心的距离，已用甲板宽度B无量纲化，u、v、w分别表示流向速度大小、横向速度大小和垂向速度大小，已用来流速度V∞无量纲化。通过对比可以看出，本文的数值计算结果和Li等人的计算结果较为吻合。数值计算得到的横向速度和垂向速度分布与实验结果相一致，而甲板中心处的流向速度与实验结果存在一定偏差，将11 个流向速度的实验数据与本文相应CFD 结果的相对误差进行平均，得到平均相对误差约为9.7%，但是总体上本文的计算结果和其他学者的研究结果比较吻合，且Reddy在其研究中已表明使用RANSk-ε湍流模型来模拟舰面流场的合理性[34]。

图3 观测线位置示意图Fig.3 Schematic of observation line

图4 实验数据和数值计算结果的对比Fig.4 Comparison of the experiment data and numerical simulation results

1.3 误差逆传播神经网络

误差逆传播（error back propagation，简称BP）神经网络是一种多层前馈神经网络，它由输入层、隐藏层、输出层三大部分组成。BP 神经网络训练的过程主要分为前向和反向传播两个阶段，前向传播将输入信号一层层传至输出层，输出层通过比较网络输出和期望输出产生误差信号，在反向传播过程中沿着误差函数梯度下降的方向，不断对网络权值和阈值进行修正，通过多次训练网络，使得最终的误差达到预期值。BP 神经网络本质上为梯度下降法，对于复杂的目标函数可能会出现“锯齿形现象”，且易出现梯度饱和现象，使得收敛速度很慢。Levenberg-Marquardt（LM）算法是梯度下降法和高斯-牛顿法的结合，其权值更新方法如式（3）所示：

式中，J(wn)为Jacobi矩阵，LM 算法引入了阻尼因子μn（μn＞0），μn数值越大表示算法越接近梯度下降法，其数值越小表示算法越接近于高斯-牛顿法。LM 算法是一种利用标准数值优化技术的快速算法，既有高斯-牛顿法的局部收敛性，又有梯度下降法的全局特性，由于利用了近似的二阶导数信息，所以LM算法比梯度下降法快得多[35]。

1.4 径向基函数神经网络

径向基函数（Radical Basis Function，简称RBF）神经网络是一种三层前馈神经网络，具有结构简单、训练简洁、学习收敛速度快等优点，能够逼近任意非线性函数并克服局部极小值问题。其基本思想就是用RBF神经元构成隐藏层空间，并对输入向量进行变换，将低维的模式输入数据变换到高维空间内，使得在低维空间内的线性不可分问题在高维空间内线性可分。在RBF网络中，输入层与隐藏层之间的连接权值可以认为是1，隐藏层对激活函数（即高斯函数）的参数进行调整，采用非线性优化策略，学习速度较慢；而输出层对线性权重进行调整，采用线性优化策略，学习速度较快。RBF神经网络对3个参数进行求解，即基函数的中心、方差和隐藏层到输出层的权值，最终得到的网络输出为

式中：σ为基函数的方差；xp为第p个输入样本（p=1，2，3，…，P），P为样本总数；ci为网络隐藏层节点的中心；wij为隐藏层到输出层的连接权值（i=1，2，3，…，h），h为隐藏层节点数；yj为第j个输出节点的实际输出。

1.5 粒子群优化方法

粒子群优化（Particle Swarm Optimization，简称PSO）算法源于对鸟类捕食行为的研究，即每只鸟（粒子）找到食物最简单有效的方法就是搜寻当前距离食物最近的鸟的周围区域。它从随机解出发，通过迭代寻找最优解，并通过适应度来评价解的品质，然后追随当前搜索到的最优值寻找全局最优解。PSO 算法初始化一群随机粒子，即随机解，通过迭代得到最优解。在每一次迭代中，粒子通过跟踪两个极值来更新自己：第一个为粒子本身找到的最优解，称为个体极值；另一个极值是整个种群目前找到的最优解，称为全局极值。

2 模型与网格

本文使用的几何模型如图5所示，是一种改进的SFS模型，称为MSFS，机库上方没有舰桥结构，但机库后面有一个加长的飞行甲板，可以看作是护卫舰的简化后体。由于之前已有学者对SFS 中有无舰桥结构的流场进行了一些研究，认为舰桥对尾流场的影响相对较小[33]，之后Tinney 和Ukeiley 在其试验研究中也采用了类似于没有舰桥的SFS2 模型，捕捉到了机库后方的分离剪切层，以及回流区中的马蹄涡和鞍点[36]。因此，本文也对SFS 机库上方的舰桥进行了拆除。为了使机库的长度有足够大的变化范围，且机库后方回流区不受甲板尾部的影响，对飞行甲板进行了加长。

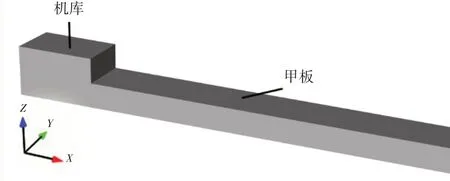
图5 MSFS几何模型示意图Fig.5 Schematic of MSFS geometry model

MSFS 的网格如图6 所示，右上角为机库周围网格的放大视图。采用多块结构网格对流体域进行划分，壁面附近生成30层六面体附面层，保证壁面y+=15。对于不同的MSFS 模型，网格单元数大约在300 万到400 万之间，具体的网格数量分布如表1 所示，随着机库长度增加，在机库上方相应地增加网格。来流的速度为10 m/s，速度方向与x轴的正方向相同，即正向来流。定义机库宽度为W、长度为L，初始高度H=0.05 m，MSFS 的总长度LL=1.5 m，通过改变机库的尺寸，来研究机库宽度、长度和高度对回流区的影响。以初始高度H为参考长度，得到的雷诺数约为3.33×104，比真实的舰船小了2 个数量级以上，但是对于舰船来说，其上层建筑是由许多钝体结构组合而成，具有尖锐边缘，已有研究认为这种结构的绕流对雷诺数并不敏感[11，37]，在Forrest 和Owen 的研究[11]中，采用1:100 的SFS2 缩比模型进行风洞实验，同时用全尺寸的模型进行CFD 计算，通过对比两者的结果，发现机库后方的流动结构在本质上是一样的。

表1 不同模型的网格单元数量分布Tab.1 Distribution of cell numbers for different models

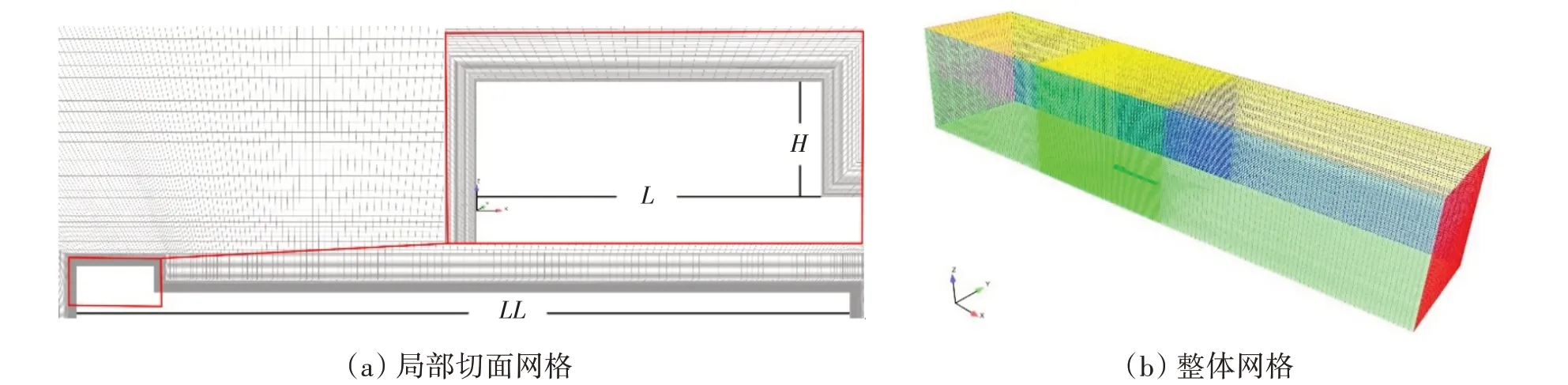
图6 MSFS网格示意图Fig.6 Schematic of MSFS grids

为了验证网格无关性，对L=3H的模型进行了三种不同网格划分，包括网格数量约为320 万的粗网格、720 万的中网格和1100 万的细网格。在纵向对称面上取一观测点，和机库等高，距机库门0.05 m，对不同网格下观测点的速度分量进行对比，如表2所示，可以发现三个方向的速度大小基本不受网格数量的影响，因此，为了提高计算效率，采用粗网格进行本文的研究。

表2 不同网格中观测点的速度分量Tab.2 Velocity components at observation points for different grids

3 流场结构分析

MSFS 纵向中切面上的流动类似于二维后台阶流动，是一种经典的分离流动，图7 中给出了机库后方的速度云图和二维流线分布，来流通过机库时会发生分离再附现象，附着的边界层在机库边缘分离，和下游的低速流动接触后，由于黏性作用形成了很薄的剪切层[38]，在机库后方产生了较大的回流区，同时剪切层中有明显的旋涡存在，当流体绕过旋涡后重新与壁面接触，形成了再附区，然后继续沿着壁面向下游流动。而对于护卫舰后体这种三维结构，来流不但在机库门上边缘发生了流动分离，还在机库门左右边缘产生了流动分离现象，最终在机库后方形成了三维回流区，导致不稳定的马蹄涡结构和呈抛物线型的再附线。图8 给出了MSFS 周围的三维流线分布图，显示了回流区的位置，包括机库上方的回流区A，机库左右两侧的回流区B，以及机库后方的回流区C。由于MSFS 为典型的尖锐边缘钝体，来流在经过前壁面后，首先在上边缘和左右边缘发生了流动分离现象，形成了1/2椭球状的回流区A和回流区B，并且再附到壁面。随着流动的发展，在机库门的三个边缘再次形成了三股分离流，并向机库后方的中心汇合，进而形成了1/4 椭球状的回流区C，可以看到其中马蹄涡的涡核位置和甲板表面的再附线，分别用蓝色线和黑色线表示。同时，图9 给出了涡结构示意图，用λ2等值面表示。λ2是一种描述涡量的方法，可以呈现出流场中的涡结构，图中用湍动能大小着色。可以看到来流在经过MSFS尖锐边缘后，在机库周围形成了不同尺度的分离涡，具有较大的速度脉动量，特别是在机库后方形成了复杂紊乱的涡结构。由于回流区中的压强较低，属于低压区，如果舰载直升机在靠近回流区的甲板上方进行起降作业时，会受到压差的影响，使机身产生向前的推力，从而引起舰载直升机的“前冲”现象。而且直升机的旋翼也会受到剪切层附近的下洗流的影响，产生俯仰力矩，可能会危及飞行安全。因此，机库后方的回流区大小对舰载直升机作业过程中的操稳性能影响极大，有必要采取相应的措施来减小回流区。

图7 机库后方二维流动结构Fig.7 2D flow structure behind the hangar

图8 MSFS周围回流区示意图Fig.8 Schematic of recirculation zone around the MSFS

图9 MSFS周围涡结构示意图Fig.9 Schematic of vortices structure around the MSFS

3.1 机库长度对回流区的影响

图10 给出了不同机库长度下MSFS 流场中的流线分布，其中所有机库的宽度W都为2H。该流线位于MSFS 的纵向中切面，用速度大小着色，蓝色表示低速区。对于不同的模型，其流场中有着相似的结构，即机库上方和后方都存在一个顺时针旋转的回流区。不同的是，当L=H时，来流在机库前壁面的上边缘发生了流动分离，形成了一个很大的回流区，在甲板面上再附，该回流区受到机库门上边缘的挤压，被分割成了两部分，一部分位于机库上方，另一部分占据了机库后方较大的空间。对于L=3H的模型，两个回流区的形成类似于L=H的模型，只是机库上方的回流区变大，机库后方的回流区变小。当L=6H时，机库上方回流区的形成是由于流动在机库前壁面的上边缘分离，之后在机库顶部末端附近发生了再附现象，而机库后方的回流区是由于流动在机库门上边缘再次发生了流动分离现象所导致，且该回流区相比前两个模型进一步减小。可以注意到，随着机库长度L的继续增加，流场结构基本不变，机库后方的回流区只有微小的变化。对于机库长度小于6H的模型，机库上壁面长度有限，机库顶部的回流区无法在机库上壁面再附，会延伸到机库后方，对甲板表面的再附位置影响比较大，所以机库后方的回流区出现了明显的变化；而对于机库长度大于6H的模型，机库上壁面有足够的空间使得机库顶部的回流区在机库上壁面再附，该回流区的扰动基本局限在机库上方，如L=9H和L=12H中所示，机库顶部末端附近的流动相对稳定，因此对机库后方的回流区影响不大。

图10 不同机库长度下的流场结构Fig.10 Flow structure of recirculation zone for different hangar lengths

3.2 机库宽度对回流区的影响

图11 中给出了不同机库宽度下MSFS 流场中的流线分布，其中所有机库的长度L都为6H。通过对比可以发现，随着机库宽度的增加，机库上方的回流区逐渐增大，再附位置不断后移至机库门上边缘，最终与机库后方的回流区混合在一起，如W=2.8H模型中的流动所示。同时，甲板上的再附位置（黑点表示）不断后移，表明机库后方的回流区也是随着机库宽度的增加有所变大，一方面是受机库上方回流区的变化影响，另一方面是由于甲板展向的空间增加。因此可以认为，机库宽度W的变化对机库后方回流区的大小也有一定的影响，可以初步推测，机库宽度W越小，则机库后方的回流区越小。

图11 不同机库宽度下的流场结构Fig.11 Flow structure of recirculation zone for different hangar widths

3.3 机库高度对回流区的影响

图12 给出了不同机库高度下MSFS 流场中的流线分布，其中所有机库的长度L都为6H，宽度都为2H。定义新的机库高度为NH，随着机库高度的增加，上方回流区的再附现象消失，并逐渐向后方移动，有和机库后方回流区混合的趋势。可以注意到，机库后方回流区的中心基本与机库等高，因此随着机库高度的增加，机库后方的回流区也被逐渐拉大。

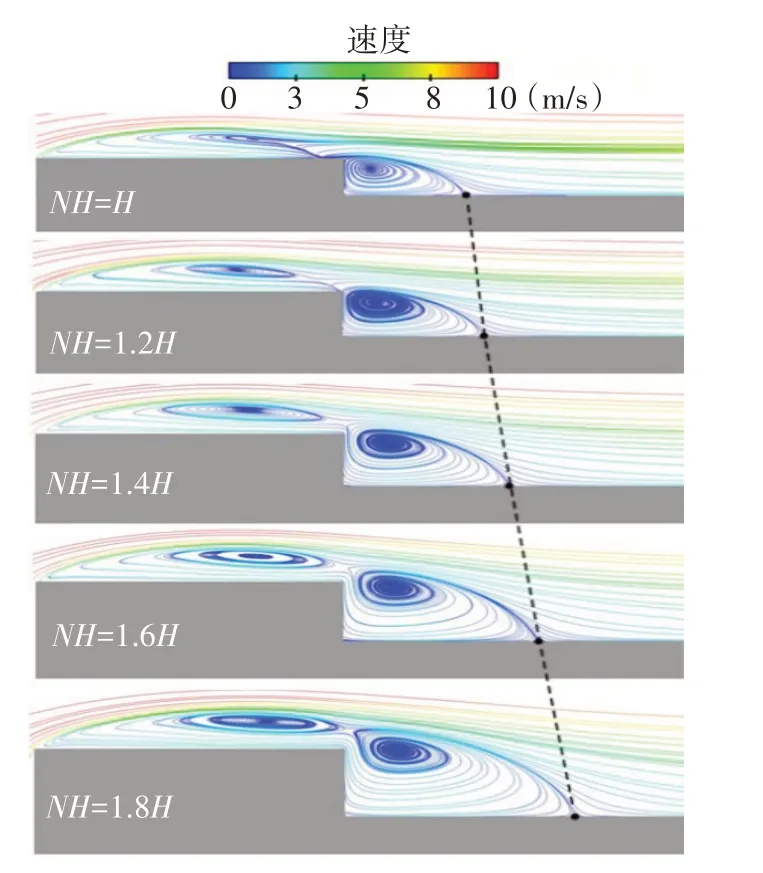
图12 不同机库高度下的流场结构Fig.12 Flow structure of recirculation zone for different hangar heights

由于本文只关注机库后方回流区的大小，所以为了描述方便和不引起混淆，下文所提到的回流区均代表机库后方的回流区。

4 流场预测与优化

通过对舰面流场的数值模拟结果分析，发现机库后方回流区的大小随着机库尺寸的变化，呈现出规律性的变化，因此神经网络可以较好地预测回流区大小。本文分别采用BP神经网络和RBF 神经网络，仅以机库长度和宽度这两个输入参数建立学习模型来进行初步研究，得到回流区的预测响应面，在该响应面上使用粒子群优化算法找出最小回流区对应的MSFS模型。

4.1 BP神经网络

首先使用Fluent 对不同模型的流场进行数值计算，所有的样本数据总和为108 个，随机抽取其中90 个样本作为训练集，剩下的18 个样本作为测试集。输入层的参数为机库的长度L和宽度W，输出层的参数为回流区的长度。采用的神经网络包含一层隐藏层，由于隐藏层的节点数对神经网络模型的预测效果有一定的影响，因此通过对隐藏层节点数从1～20 进行多次重复遍历，根据预测误差的大小，选取比较好的节点数，本文最终选取的隐藏层节点数为8。同时，使用粒子群算法，对BP神经网络的初始权值和阈值进行优化后，再开始训练网络，能较快地达到预期误差范围。网络训练算法选取Levenberg-Marquardt 算法，隐藏层激活函数为tansig函数，输出层激活函数为purelin函数。最终的网络模型结构如图13所示。

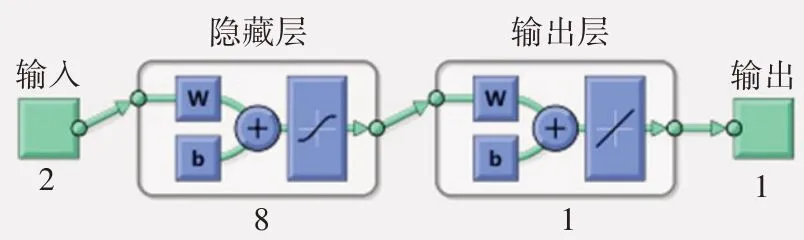
图13 网络模型结构Fig.13 Structure of network model

4.1.1 预测效果

图14给出了训练样本（Train）、验证样本（Valida⁃tion）和测试样本（Test）的均方差随训练次数的变化曲线。当训练样本在对网络训练时，网络的输出会逐步逼近目标输出，从而减小目标误差，但是在这一训练过程中，每训练一次都会利用验证样本来检验网络对验证样本的拟合能力，即网络在验证样本的输入下其输出误差是否也呈现下降的趋势，如果连续多次验证样本的输出误差都不再减小或者甚至增大，那么训练就会终止，防止训练出的网络过拟合。从图中可以看到，验证样本的均方差在第65 次训练后逐渐变大，因此最好的网络是经过65 次训练的网络。

图14 均方差变化趋势Fig.14 Variation of mean squared error

将测试集中的18 个样本在训练后的BP 神经网络中进行预测，图15 中给出了回流区长度的预测值和期望值的对比，其中回流区长度已用高度H无量纲化。对比可以发现，测试集中的预测值和期望值基本一致，无明显偏差。在图16 中能直观地看到预测值和期望值之间的相对误差，对于这18 个测试样本，最大相对误差约为0.9%。

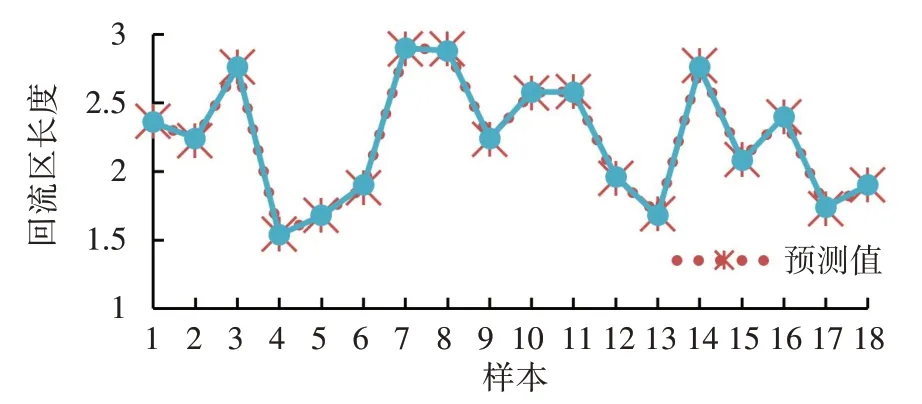
图15 BP预测结果对比Fig.15 Comparison of BP predicted results

图16 BP相对误差分析Fig.16 Analysis of BP relative error

4.1.2 流场优化

基于SFS 和SFS2 的机库宽度都为2.25H，机库长度分别为7.5H和11.5H，如果机库过窄或过短会导致机库空间狭小，机库太宽或太长会导致整个舰船的尺寸增加，因此在优化过程中限定MSFS 机库宽度范围为1.5H～3H，机库长度范围为4H～20H。

根据得到的BP 神经网络，作出了回流区长度的预测响应面，如图17所示，图中的坐标已用高度H无量纲化。可以看出：当W保持不变时，回流区长度随着L的增加先减小后增大；当L保持不变时，回流区长度随着W的增加呈现出不同程度的增大。由响应面可以推测出最小的回流区存在于W=1.5H，L=6.5H附近。

图17 BP预测结果响应面Fig.17 Response surface of BP predicted results

通过粒子群优化算法对舰面流场进行优化，找到了最小的回流区长度为1.93H，对应的机库宽度为1.5H，机库长度为6.47H。为了验证优化结果的准确性，在Fluent 中对优化模型进行数值模拟计算，得到纵向中切面的流线图，如图18 所示。其中横坐标表示距MSFS前端的长度，已用高度H无量纲化，机库门的位置为6.47H，甲板再附位置约为8.41H。得到回流区长度为1.94H，和优化预测结果相比，相对误差约为0.5%，可以认为优化效果比较好。

图18 BP优化模型流场结构Fig.18 Flow structure of BP optimized model

4.2 RBF神经网络

在RBF神经网络中使用的训练样本和预测样本与BP神经网络中的样本保持一致，采用的是正规化RBF 神经网络，即隐藏层神经元个数和输入样本数量相等，需要调整的参数为扩展常数spread，其值越大，输出结果越光滑，但太大的值会导致数值计算上的困难，影响预测效果。因此通过遍历不同的spread值，找到误差较小的神经网络，最终选取spread的值为3.01。

4.2.1 预测效果

同样将测试集中的18个样本在训练后的RBF神经网络中进行预测，从图19中的对比结果可以发现测试集中的预测值和期望值基本一致，也无明显偏差。在图20中能直观地看到预测值和期望值之间的相对误差，RBF神经网络得到的最大相对误差约为2.2%，比BP神经网络的相对误差稍大，但在可接受范围内。

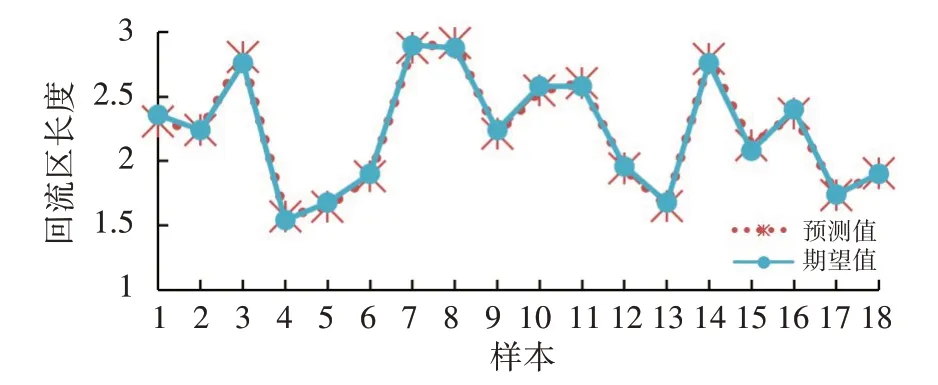
图19 RBF预测结果对比Fig.19 Comparison of RBF predicted results

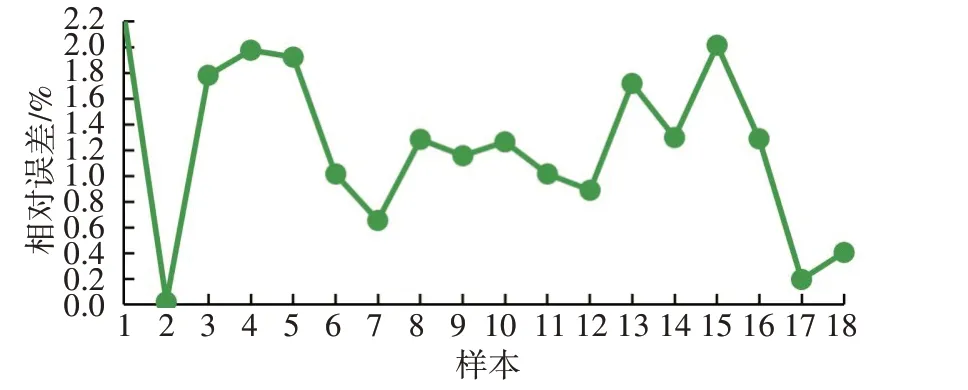
图20 RBF相对误差分析Fig.20 Analysis of RBF relative error

4.2.2 流场优化

根据得到的RBF 神经网络，作出了回流区长度的预测响应面，如图21所示，图中的坐标已用高度H无量纲化。对比图17 中的BP 预测结果响应面，两种神经网络得到的预测响应面在整体上较为相似，都是回流区长度随着L的增加先减小后增大，随着W的增加呈现出不同程度的增大，且回流区长度的最大值出现在W较大、L较小的模型中。不同的是，在L=4H和L=5H对应的模型中，两种方法得到的回流区长度出现了偏差，RBF 神经网络预测的回流区长度最大值超过了5.8H，而BP神经网络预测的回流区最大值不超过5.4H。这是因为初始样本中没有包括L=4H和L=5H的数据，在预测响应面的边界时主要通过外插法进行，导致对两种方法下学习模型的建立有较大的影响，但是从RBF 预测结果响应面中也可以推测出最小的回流区存在于W=1.5H和L=6.5H附近，和BP 神经网络推测一致，因此两种预测响应面的差异对流场优化没有明显影响。

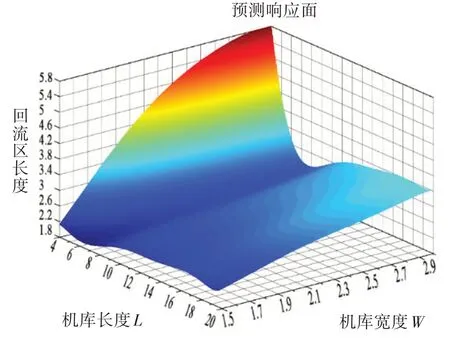
图21 RBF预测结果响应面Fig.21 Response surface of RBF predicted results

最后通过粒子群优化算法找到了RBF神经网络中最小的回流区长度也为1.93H，对应的机库宽度为1.5H，但是机库长度为6.33H，和BP优化结果有所不同，因此对该优化模型进行数值模拟计算，得到纵向中切面的流线图，如图22 所示。机库门的位置为6.33H，甲板再附位置约为8.27H，得到回流区长度为1.94H，和BP优化模型的数值计算结果相同，相对误差也约为0.5%，可以认为RBF 神经网络和BP 神经网络得到了较为一致的优化结果。

图22 RBF优化模型流场结构Fig.22 Flow structure of RBF optimized model

5 结 论

由于流动分离现象，机库后方会产生不稳定的回流区，影响舰载直升机的甲板作业。因此本文基于CFD方法和人工神经网络方法的结合，在舰面流场优化方面做了初步尝试。将BP和RBF两种神经网络方法应用到舰船尾流场的预测中，结合粒子群优化算法，来探寻机库后方最小回流区对应的MS⁃FS模型。

研究结果表明，回流区长度随着L的增加先减小后增大，随着W和NH的增加呈现出不同程度的增大。和数值模拟结果相比，BP 神经网络预测得到的回流区长度最大相对误差约为0.9%，RBF 神经网络预测得到的最大相对误差约为2.2%，都在可接受范围内。BP和RBF两种神经网络得到的预测响应面在整体上较为相似，且预测的最小的回流区长度相同。因此，使用人工神经网络方法预测舰船尾流场信息具有可行性和准确性，舰船在设计初期可以考虑结合CFD 和人工神经网络方法对舰船上的目标结构进行优化，以达到改善舰面气流场的目的。特别地，对于驱逐舰或护卫舰这种具有尾部甲板结构的舰船，为了减小机库后方的回流区以利于舰载直升机起降，可以基于本文的研究结果，在保证机库内部空间足够的情况下，尽可能地减小机库的高度和宽度，机库的长度建议大于6 倍的机库高度，但要注意过长的机库会占据飞行甲板的空间，具体的长度应该在确定高度和宽度后，以长度为输入参数建立学习模型，得到最终的优化结果。

本文目前的研究内容是对神经网络应用在舰面流场中的初步探索，采用模型较为简单，后期将对学习模型的输入参数和输出参数增加复杂性，一方面以复杂机库的多种尺寸和位置作为输入来预测回流区响应面，进而得到多维度下的优化结构；另一方面以来流风速风向和舰船的运动参数等作为输入参数，来预测机库后方的回流区范围和涡结构区域，期望建立舰面流场预警系统，来保障甲板作业的安全性。