热工过程海量数据的高质量样本提取方法及应用
何 康, 汪 勇, 陈荣泽, 任少君, 司风琪
(1. 东南大学 能源与环境学院, 南京 210096;2. 上海发电设备成套设计研究院有限责任公司, 上海 200240)
机器学习以训练样本集为基础,采用一系列数学方法从数据中提取变量间的关联性,并且形成相应的数学表达式。实际上,根据系统特性的不同,变量间的关联性会呈现出不同的特点,如静态特性和动态特性、线性和非线性、单模态和多模态等。神经网络作为常用的数据驱动建模方法之一[1-3],由于该方法直接面对样本本身,因此当训练样本无法体现变量间的关联性时,所建立的模型也难以反映系统真实的特性。因此,高质量样本是保证神经网络模型准确性的重要前提。一般而言,高质量样本需要具备以下性质:
(1) 静态特性。电站信息化系统保存了设备海量的运行数据,虽然这些数据能够真实地反映出系统实际的运行状态,但其中也包含了大量的动态过程数据,而这些数据无法准确反映系统的静态特性。因此,需要对原始数据进行筛选才能得到适用于静态模型的训练样本。
(2) 分布均匀。在实际运行过程中,电站设备的运行模式会周期性发生变化,进而产生大量冗余数据。因此,对原始数据进行样本约简不仅可以找到反映过程特性的主要因素,而且能够减小样本规模,提升神经网络模型的学习速率和精度。此外,还会存在设备在某些工况下运行样本不足的情形,对于这类样本则需要进行扩展和补充,从而提升训练样本分布的均匀性。
综上所述,为了提高神经网络模型的建模效果,以自联想神经网络为研究对象,提出了一种面向海量过程数据的高质量样本提取方法,主要包括基于隐变量的系统级稳态因子计算、海量样本约简和少数类工况样本过采样均衡三个步骤,最后利用实际工程案例验证了所提方法的有效性。
1 基于隐变量的系统级稳态因子计算
1.1 单变量稳态因子计算方法
研究学者们已经通过提取固定时间序列的趋势特征[4]和统计特征[5]来反映系统单变量的稳态程度,并通过与经验值进行比较来剔除动态样本。相比于趋势特征法,统计特征法不依赖于趋势的提取速度,对训练样本及滑动窗口的敏感度低。R检验法[6]作为一种统计特征法,其对滤波后的数据采用两种不同方法得到方差的无偏估计并建立检验统计量。该方法不需要时间窗,采用的逻辑运算少,占用存储空间小,且具有较高的计算速度。因此,采用R检验法进行单变量的稳态因子计算。假设样本X∈Rn×p(R为实数组成的矩阵),n为样本数量,p为参数个数,Xi表示X的第i组样本。R检验法的具体步骤如下。
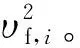
Xf,i=λ1Xi+(1-λ1)Xf,i-1
(1)
(2)
式中:λ1、λ2均为滤波系数,均取0.2[7]。
(3)
式中:λ3为滤波系数,取0.1[7]。
(4)
(5)
(5) 计算Xi的稳态因子Ri[7]。
(6)
(6) 返回步骤2进行计算,直至所有的Xi计算完毕。
1.2 多变量稳态因子计算
热工过程常涉及到多变量,通过单变量稳态判定并不能反映多变量系统工况的变化,因此需要研究面向系统级的多变量稳态因子计算方法。
隐变量分析作为一种特征提取方法,它将高维度数据经过映射转换到低维度空间,并且将新得到的特征变量作为系统的隐变量[8]。主成分分析(PCA)法是一种常见的隐变量分析方法,它通过线性映射将原始数据映射到低维度空间,只需要使用少量特征就能够解释原始数据间的相关性。图1为PCA法的基本原理示意图,原始高维数据X经过线性映射投影到低维空间得到低维数据Z,即完成了对原始数据的降维处理。因此,为了更好地提取数据的特征,采用PCA法[9]提取系统隐变量,并通过隐变量的稳态程度来表征系统数据的稳态程度。

图1 PCA法的基本原理示意图
图2为基于隐变量的系统级稳态因子计算原理示意图。具体计算步骤如下:
(1) 使用PCA法得到关于X的系统级隐变量Z及第k个隐变量对应的贡献率Gk。
(2) 根据1.1节中的方法计算第i组样本Xi的第k个隐变量的稳态因子Rk,i。
(3) 计算第i组样本Xi的系统级稳态因子Rsys,i,并得到系统级稳态因子序列Rsys。
(7)
Rsys={Rsys,1,Rsys,2,…,Rsys,n}
(8)
式中:m为隐变量的个数。

图2 基于隐变量的系统级稳态因子计算流程
2 基于稳态权重的压缩近邻(SWCNN)的样本约简
机组设备常常在一个或多个工况下长时间运行,所产生的运行数据中会存在大量冗余信息。为减少冗余信息的影响,有学者提出了一种压缩近邻(CNN)法[10],按照最近邻规则将原始数据集压缩成一个新的数据集。但CNN法依据样本和压缩集已有各样本之间距离与阈值的关系决定样本是否加入压缩集,并没有考虑样本的稳态属性。结合系统级稳态因子计算方法,提出了SWCNN法,其具体计算步骤如下。
(1) 初始化压缩集X’为空集,初始距离阈值为D,稳态权重序列集合W为空集。计算样本X的稳态因子序列Rsys。
(2) 判断X是否为空,如果为空进入步骤7。
(3) 按照式(9)计算Xi的稳态权重Wi,按照式(10)计算权重阈值Di。
(9)
Di=D/Wi
(10)

(i=1,2,…,l;s=1,2,…,l)
(11)
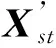
(5) 从样本集X中剔除样本Xi并记作:
X=X-Xi
(12)
如果Dmin大于权重阈值Di,则将Xi归入压缩集X’并记作:
X’=X’∪Xi
(13)
同时,将Xi对应的稳态权重Wi归入稳态权重序列W,并记作:
W=W∪Wi
(14)
(6) 返回步骤2进行下一次计算。
(7) 输出压缩集X’及对应的稳态权重序列W。
3 基于稳态权重的合成少数类过采样(SWSMOTE)
机组在某些工况下的运行时间较短,所产生的运行数据量较少甚至没有运行数据,从而造成样本分布不均。为减少样本分布不均匀对模型的影响,主要从欠采样[11]和过采样两个方面进行研究。欠采样通过减少多数类样本数量以实现样本的均匀分布,但这种方法会遗失部分有用信息。与欠采样相比,过采样增加少数类样本以实现样本的均匀分布,这种方法在降低过拟合的可能性的同时还可以避免信息遗失,因此更适合处理热工过程数据。现有的过采样算法研究基本只考虑了样本的距离因素,未考虑样本间的差异性。因此,提出了一种基于稳态权重的合成少数类过采样(SWSMOTE)法,其具体计算步骤如下。
(1) 对于原始数据集X,采用SWCNN法得到压缩集X’和对应的稳态权重序列W,并且利用1.2节计算得到的系统隐变量将压缩数据集X’分成J类,将第j类的样本个数记作dj。初始化新样本集合Q’为空集,j=1和该类的样本需求数量dj,max。
(2) 如果dj=dj,max,则进入步骤4。
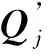
(15)
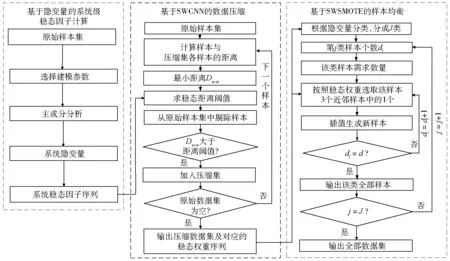
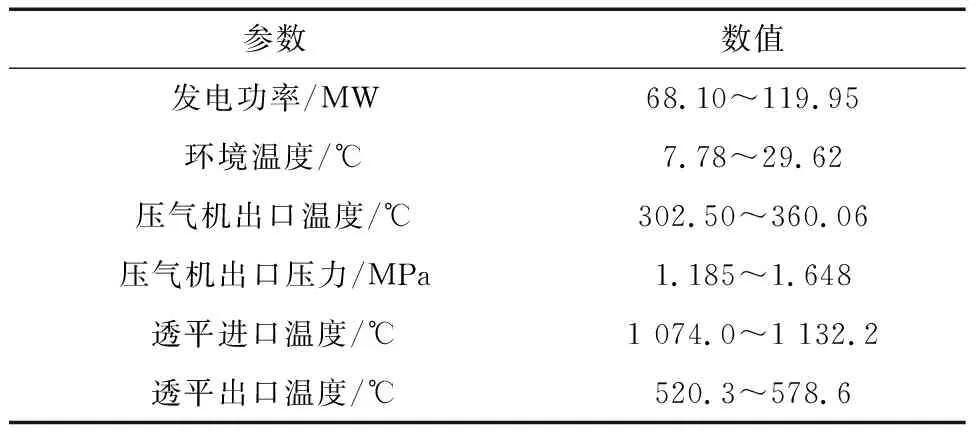
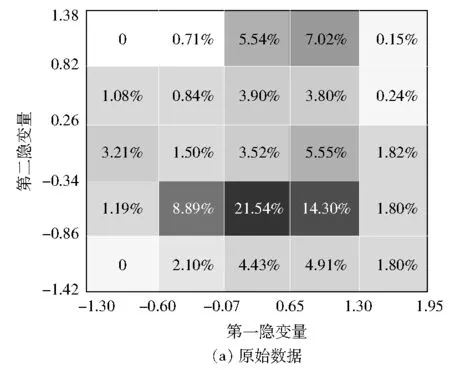
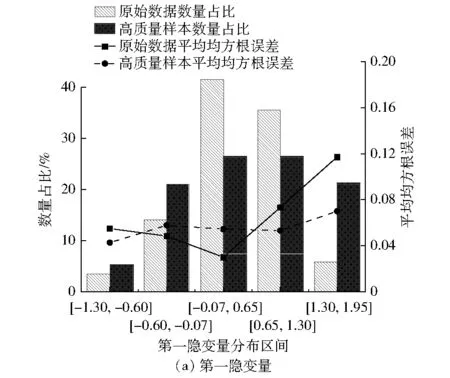
(4) 如果j (5) 将压缩样本集X’和生成的新样本集Q’合并,输出全部样本集Xnew,记作: Xnew=X’∪Q’ (16) 图3为热工过程海量数据的高质量样本提取流程图,整个算法的步骤总结如下: (1) 使用系统级稳态因子的计算方法获取关于X的系统隐变量和稳态因子序列。 (2) 根据计算得到的系统稳态因子,利用SWCNN法对原始数据进行压缩约简,得到压缩集及对应的稳态权重序列,并将其作为SWSMOTE法的输入。 (3) 根据SWCNN法得到的压缩集和稳态权重序列,以及系统级稳态因子计算得到的系统隐变量,利用SWSMOTE法对样本进行均衡,得到高质量样本集。 图3 热工过程的高质量样本提取方法 燃气轮机是燃气-蒸汽联合循环机组的核心设备,其运行状态对机组的安全稳定运行有着重要作用。研究对象是某额定功率为130 MW的燃气轮机,其系统结构见图4。 图4 燃气轮机系统结构 选用该燃气轮机的发电功率、环境温度、压气机出口温度、压气机出口压力、透平进口温度、透平出口温度这6个过程参数作为模型变量,各参数运行范围见表1。从分散控制系统(DCS)中采集14 385组运行数据作为原始训练样本。同时,采用MATLAB软件进行计算分析。 表1 6个过程参数的运行范围 对这6个参数进行主成分分析,选择2个主成分作为隐变量,其对系统的贡献率之和为94.26%。计算样本稳态因子序列作为近邻压缩计算的权重阈值,并且对原始样本进行约简。采用系统级隐变量对约简后的数据进行分类,获得每种类别的样本数量。根据样本数量的不平衡率,用SWSMOTE法进行插值,并且设定dj,max=max{d1,d2,…,dJ}。在插值过程中,当类别中样本数量小于6时,插值效果较差,因此针对该类情况不进行插值。 图5为原始数据和高质量样本的分布,图中数值表示该类样本数量占总样本数量的比值。由图5可得:原始数据分布不均匀,而提取后的高质量样本分布得较为均匀,除个别类别样本数量太少的工况以外,其他工况样本数量均占总样本数量的5%左右。 图5 原始数据和高质量样本的分布 自联想神经网络(AANN)是在1987年由Ballard针对编码/解码问题首先提出的,其网络原型是一种具有对称拓扑结构的五层前馈传递网络。AANN首先通过输入层、映射层和瓶颈层实现了输入数据信息的压缩。从网络输入的高维参数空间中提取了反映系统结构的最具代表性的低维子空间,同时有效地滤去了测量数据中的噪声和测量误差,再通过瓶颈层、解映射层和输出层实现数据的解压缩,将前面压缩的信息还原到各个参数值,实现各测量数据的重构。AANN的具体结构可见参考文献[12]。采用AANN[12]分别对经过稳态筛选的原始数据和高质量样本进行训练,得到2个模型,并且从模型精度和训练时间对模型性能进行评价。模型学习率设为0.015,训练结束条件为各样本达到最大迭代次数(2 500)或者模型精度达到预设精度(0.05)。训练完成后利用原始数据进行测试,同时采用均方根误差衡量模型效果。均方根误差ERMS的计算公式为: (17) 图6展示了测试样本在不同第一隐变量和第二隐变量区间下平均均方根误差的分布情况。 图6 不同第一隐变量和第二隐变量分布区间下样本测试平均均方根误差 由图6可得:从精度来看,原始数据在样本分布密集处的平均均方根误差较小,精度较高。第一隐变量在[-0.07,0.56],样本数量占比为41.09%,平均均方根误差为0.03;第二隐变量在[-0.86,-0.34],样本数量占比为50.25%,平均均方根误差为0.04。而在样本数量较少的区域,模型测试误差呈现出直线上升的趋势。第一隐变量在[1.30,1.95],样本数量占比为5.81%,平均均方根误差为0.12;第二隐变量在样本分布较少的[0.26,0.82],样本数量占比为8.85%,而平均均方根误差已经达到2.78。经过SWSMOTE法处理后的数据,虽然在样本分布密集处的精度有所下降,但是在其他区域内的平均均方根误差有明显的下降,第一隐变量在[1.30,1.95]和第二隐变量在[0.26,0.82]时,平均均方根误差已经分别降至0.07和0.05,其他区域样本的平均均方根误差在0.06左右。总体来说,由于个别区域只有0~6个样本,无法采用SWSMOTE法,但是所提出的算法大大改善了原始数据分布不均匀所带来的误差不均衡的问题,总体平均均方根误差也较为均衡。 图7为使用原始数据和高质量样本建模时的预处理时间和训练时间的对比。从学习时间来看,由于样本数量的增加,采用原始数据对AANN模型进行训练的时间高达535.25 s,使用高质量样本进行数据预处理和模型训练时间加起来仅为49.68 s,模型训练时间减少90%。综上所述,采用高质量样本所建立的模型不但提高了模型精度,还减少了模型学习时间。 图7 预处理时间和训练时间的对比 提出了一种面向热工过程海量运行数据的高质量样本提取方法,该方法通过PCA法提取了参数主要特征的贡献率,结合SWCNN法对原始样本进行约简,降低了样本规模。此外,该方法引入了SWSMOTE技术对少数类工况进行过采样,进一步提升了训练样本的均匀性。以燃气轮机为对象进行案列分析,分别采用原始数据和高质量样本建立AANN模型,结果表明:提出的高质量样本提取方法将燃气轮机的原始数据数量压缩到10%左右,模型平均均方根误差从0.042下降至0.031,模型训练时间减少90%。在剔除了冗余信息的同时,最大程度地保留了样本稳态信息,改善了样本的不均匀属性所带来的精度不高的问题,具有广阔的工程应用前景。4 高质量样本提取流程
5 结果分析
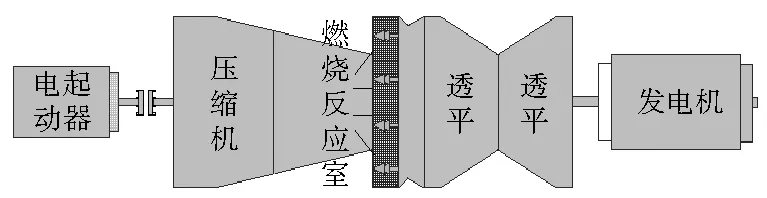
5.1 燃气轮机系统模型
5.2 高质量样本提取
5.3 模型训练与测试


6 结语

