基于改进最小二乘支持向量机的一次风机状态预测方法研究
王 帝, 李 治, 汪 勇, 邓志成, 孙 猛,方 超, 丁 刚, 肖伯乐
(上海发电设备成套设计研究院有限责任公司, 上海 200240)
在“双碳”目标下,大电网的稳定运行离不开火电机组的调度、调控和管理[1],而风机作为火电厂的重要辅机,其运行状态与发电机组的安全性和经济性密切相关。准确预测风机状态对于减少火电机组的非计划停机,降低火电厂的运行成本,提高电力系统的安全性具有重要意义。
国内外学者对风机及其他电厂设备的状态预测和故障预警开展了大量研究[2]。潘岚川[3]以一次风机为研究对象,分别建立了卷积神经网络(CNN)和遗传算法-卷积神经网络(GA-CNN)的风机轴承振动模型,并验证了这2种算法的有效性。欧阳刚[4]通过对风机典型运行特性的分析,提出一种基于最小二乘支持向量机(LSSVM)的一次风机振动状态估计和故障预警方法,但未对模型中的超参数进行寻优。潘召涛[5]以一次风机为研究对象,使用数据挖掘技术优化风机故障预警系统,使预警时间提前了2.5 h。何玉柱[6]针对一次风机常见的轴承温度异常和风机振动异常故障,应用相关算法设计了智能预警系统,结果表明该系统能够快速排除故障。范海东等[7]提出一种基于自编码网络与dropout机制的发电设备故障预警模型,利用该模型能在发电设备故障潜伏期准确发出预警信息。高泽明等[8]建立了一种基于多元状态估计技术(MEST)的故障预警模型,通过Matlab仿真程序验证了模型的可行性和有效性。彭道刚等[9]提出一种基于长短期记忆网络(LSTM)和支持向量机(SVM)的燃气轮机压气机故障预警方法。牛玉广等[10]为了有效识别辅机在运行过程中的故障,提出了一种基于多元状态估计与自适应阈值的电站辅机故障预警方法。Amirkhani等[11]采用一种基于蒙特卡罗仿真的自适应阈值方法,研究了电厂燃气轮机作为非线性不确定系统的鲁棒故障诊断问题。Kordestani等[12]总结了各领域设备和系统故障诊断预测的通用数学方法,并展望了未来的研究方向。Li等[13]基于一次风机油泵电流的实时数据,采用万有引力神经网络方法建立了一次风机振动故障诊断模型,通过仿真验证了该模型的精度。上述研究仍存在以下2点不足:(1) 风机系统工况复杂,故障种类繁多,且历史数据不完整,仅靠增大输入数据的时间尺度无法有效提高预测精度;(2) 训练机器学习模型时,模型中超参数的选择有较大的主观性,超参数质量低会导致训练过程出现过拟合、局部最优或算力浪费等问题。
针对上述问题,笔者提出了一种基于改进天牛须搜索算法(IBAS)优化的LSSVM一次风机状态预测模型。首先,基于“系统+部件”的思想多维度地构建了原始特征体系,采用皮尔逊相关系数对各维度数据降维处理;其次,改进了天牛须搜索算法(BAS),应用IBAS对LSSVM模型中的超参数进行寻优,建立了完整的一次风机状态预测模型;最后,采用国内某电厂的一次风机实测数据进行了算例分析。
1 算法原理
1.1 最小二乘支持向量机
1999年,Suykens和Vandewalle等在支持向量机的基础上提出LSSVM,该算法在目标函数中加入了平方误差项,约束条件从SVM的不等式约束变为等式约束,从而将SVM的求解从二次规划问题转化为线性方程组问题,降低了计算复杂程度,提高了训练速度,有助于利用海量电厂数据有效地预测并分析设备状态[14]。LSSVM的具体步骤如下。
给定1组训练样本集S为:
S={(xi,yi)},i=1,2,…,N
(1)
式中:xi为预测的输入向量,xi∈Rn;n为输入向量的维数;yi为预测的输出向量,yi∈Rn;N为训练样本的数量。
LSSVM的目标是构造如下的预测函数:
f(x)=ω·φ(x)+b
(2)
式中:ω为权重向量;φ(x)为LSSVM的核函数,可以将输入样本映射到高维特征空间进行线性回归求解;b为偏差向量;f(x)为预测函数。
根据结构风险最小化原理,LSSVM优化问题的目标函数表达式为:
式中:J(·)为目标函数;ei为拟合误差向量;γ为惩罚因子,用来控制误差的惩罚程度。
对于等式约束的优化问题,可采用构造拉格朗日函数L(·)求解,引入拉格朗日乘子向量λi,有表达式如下:
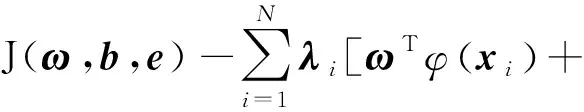
b+ei-yi]
(5)
根据KKT(Karush Kuhn Tucker)条件,对式(5)优化如下:
(6)
通过消去特征空间的权重向量ω和拟合误差向量ei,得到如下线性方程:
(7)
式中:I为单位矩阵,IN∈RN;Ωij=φT(xi)φ(xj)。
根据Mercer条件,记核函数为K(xi,xj)=Ωij=φT(xi)φ(xj),表示输入空间到高维特征空间的非线性映射。
通过求解式(7)线性方程组,得到一次风机状态预测的回归函数[14]:
(8)
核函数的选择对LSSVM的预测性能有很大影响,选择恰当的核函数可以提高预测算法的效率,减少预测时间,提升预测性能。常见的核函数有傅里叶核函数、径向基核函数、Sigmoid核函数和多项式核函数等。由于径向基核函数具有径向对称、光滑性好及泛化能力强的特点,笔者选取径向基核函数作为预测模型的核函数。其表达式为:
(9)
式中:σ为核函数的标准化参数。
在径向基核函数的LSSVM预测模型中,标准化参数反映了训练样本数据分布特性,惩罚因子决定了训练误差大小和泛化能力的强弱,这2个超参数直接影响模型的预测效果。在传统的LSSVM预测中,这2个超参数往往根据经验选取[14],为提高模型的预测性能,选取智能优化算法对2个超参数进行寻优。
1.2 天牛须搜索算法
天牛须搜索算法是由Jiang等[15]于2017年提出的智能优化算法,与其他仿生类算法不同,BAS是一种单体搜索算法,具有原理简单、参数少、计算量少等优点,在处理低维优化目标时具有较大优势。BAS的原理为模仿自然界中天牛的觅食行为,通过位于头部的触角感知食物的气味强弱,当其左触角感受到更强烈的食物气味时,天牛向左飞行,反之,向右飞行。天牛的觅食过程在本质上是寻优的过程,通过一次次迭代,最终找到食物的位置[15]。BAS的具体步骤[15]如下。
步骤(1):参数初始化。设初始化天牛质心位置x0、天牛左右须间距d、步长收缩因子和迭代次数t。天牛须朝向定义为随机的方向向量。
(10)
式中:k为寻优维度;rank(·)为随机函数。
步骤(2):建立天牛左右须的空间坐标。其表达式为:
(11)
式中:xr,t、xl,t分别为天牛的右须和左须在第t次迭代时的空间坐标;xt为第t次迭代时天牛质心的位置。
步骤(3):建立适应度函数。
(12)
式中:f(·)为适应度函数,适应度函数代表了气味浓度的判断标准;fl,t、fr,t分别为天牛左右须第t次迭代时的适应度值。
通过比较天牛左右须的适应度值大小,决定天牛下一步的移动方向。
步骤(4):建立天牛移动模型。
(13)
式中:δt为第t次迭代时的步长因子,δt=c·d·ηt-1,其中c为大于1的常数,η为步长收缩因子;sign(·)为符号函数。
传统的BAS通过计算比较天牛左右须的适应度值选择寻优方向,进而不断迭代质心的位置坐标,实现最优化搜索。该方法在实际应用中存在以下问题:(1) 作为从单点出发寻优的算法,BAS具有陷入局部最优缺陷,其寻优结果严重依赖初始化参数;(2) 算法中对天牛左右须位置坐标和适应度值的计算仅仅是为了比较下一步质心移动的方向,属于一次性计算量,当质心位置移动后,上一步计算的位置坐标和适应度值就再无意义,造成算力浪费,降低了算法的效率;(3) 算法中质心移动的搜索步长是递减的,即如果前期搜索过程错过了全局最优值,后期迭代可能因步长变短无法接近全局最优值,使搜索结果陷入局部最优。
1.3 IBAS
为了提升预测模型的精度并充分利用模型算力,针对上述问题对传统BAS改进如下:(1) 为解决天牛须搜索算法因初始值选择不当而导致的局部最优问题,采用网格化寻优方法对参数初始值进行快速初筛。首先利用网格搜索法的较广搜索范围和较大步长获取2个超参数的全局优化初始值,然后以全局寻优获得的2个超参数值作为BAS的质心初始值进行寻优计算;(2) 为充分利用算力,并使算法跳出局部最优,采用混合步长的方法改进BAS,IBAS提升了算法的效率和稳定性。
改进后的天牛质心移动模型为:
(14)
改进后的天牛质心坐标更新路径有3种选择。在每一步更新时,计算fl,t、fr,t后,与fm,t比较。如果fl,t最小,表示xl,t更接近最优值,质心坐标更新为xl,t;如果fr,t最小,表示xr,t更接近最优值,质心坐标更新为xr,t;如果fm,t最小,表示xm,t更接近最优值,质心坐标更新为xm,t。在前2种路径下,xt与xt-1间隔的步长为d,远小于第3种路径下xt与xt-1间隔的步长δt。改进后的BAS利用原算法中的一次性计算量参与模型寻优流程,实现了基于混合步长的寻优搜索,提高了BAS的效率,增强了全局寻优能力。
2 模型搭建
2. 1 特征选择
一次风机监测信号包括振动、温度、压力、流量、电流和开度等信号特征,其变量较多,各参数之间存在一定的耦合性。输入特征过多会增大模型的计算量,降低模型的效率和精度,因此需要对其降维处理。根据皮尔逊相关系数r选择特征变量,在统计学中,皮尔逊相关系数可表征2个变量之间的线性相关强度,2个变量的相关系数计算公式[3]如下:

(15)
式中:cov(·)为协方差函数;E(·)为数学期望函数;ξ为均方差;U、V为2个变量。
如果相关系数的绝对值大于0.5,则认为这2个变量具有强相关性。
2.2 基于IBAS-LSSVM的预测模型
由第1.1节中LSSVM模型可知,在一次风机状态预测中,超参数的选择会直接影响预测精度。因此,选择IBAS优化LSSVM的2个超参数(γ,σ)。IBAS-LSSVM预测模型流程如图1所示。

图1 IBAS-LSSVM预测模型流程
具体步骤如下:
步骤(1):搜集历史数据,依次完成数据预处理、归一化处理和特征选择。
步骤(2):初始化LSSVM参数(γ,σ);初始化网格搜索参数,将超参数γ和σ的范围设置为0~30,步长设置为5。
步骤(3):依次计算每个网格点的计算精度,获取超参数γ和σ的全局优化值。
步骤(4):初始化IBAS参数,包括天牛初始质心位置x0、天牛左右须间距d、步长收缩因子和迭代次数。将全局寻优获得的2个超参数值作为天牛须质心初始值x0,设最优位置xbest=x0,根据式(11)计算出天牛左右须的空间坐标。
步骤(5):确定适应度函数,作为天牛须气味浓度判断标准。本算法采用模型预测值和实际值的方差作为适应度函数。
(16)

步骤(6):计算初始适应度函数值fbest=f(xbest)。
步骤(7):更新天牛左右须位置坐标xl,t、xr,t及其适应度值fl,t、fr,t;计算质心预更新位置坐标xm,t及其适应度值fm,t。
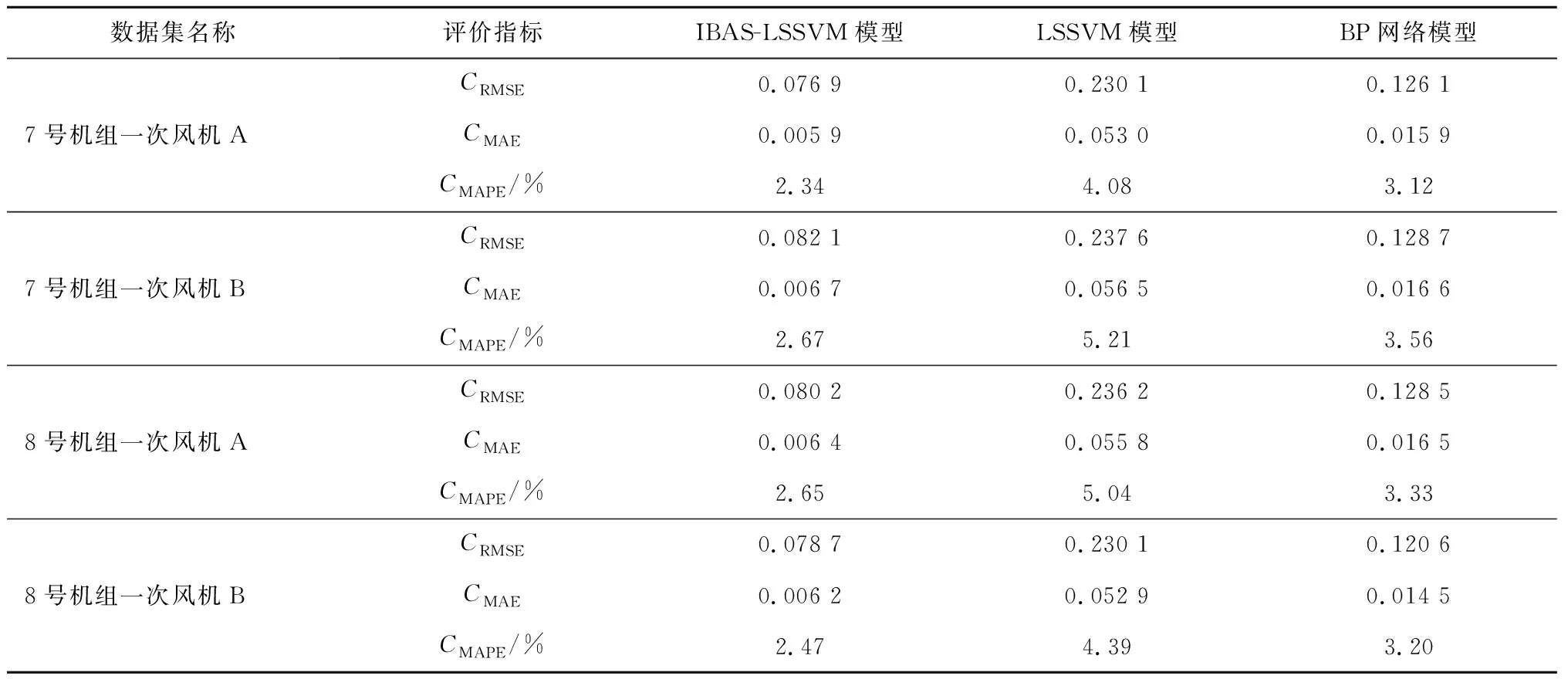
步骤(8):根据式(13)和式(14)更新天牛质心坐标xt,并计算出适应度函数f(xt)。检验质心更新条件, 若f(xt) 步骤(9):判断是否达到最大迭代次数(100)或适应度值是否达到预设精度(e-10)。若达到条件则继续,否则跳转至步骤(7),更新天牛步长后继续迭代。 步骤(10):生成γ、σ的最优解,代入到LSSVM模型中完成一次风机状态预测。 所使用的一次风机运行数据来自某电厂7号和8号发电机组。每台机组配备A、B 2台轴流式一次风机,共收集4套一次风机运行数据。轴流式一次风机的结构如图2所示。一次风机测点数据由电厂监控信息系统(SIS)采集与存储,并导出成csv数据文件。数据采集时间为2021年1月1日至12月31日共365 d,每天采集24个时间点,采样间隔为1 h。 图2 轴流式一次风机结构示意图 有效地分解和聚合原始特征能更好地反映问题的本质,提高预测模型的精度。根据一次风机的结构和运行机理,按照“系统+部件”的思想,多维度选取一次风机的状态特征,构建特征体系,见图3。 图3 一次风机状态预测模型特征体系 系统级维度的特征系统包括发电机组的输出电气量参数、锅炉运行参数及机组负荷,表征发电机组总体运行状态,将一次风机的运行状态映射到系统级层面;部件级维度的子特征体系分为风机本体部件和驱动电机部件2部分,风机本体考虑风量参数、轴承状态参数和控制系统参数,驱动电机考虑电机绕组参数和轴承状态参数,这些参数表征风机本体和驱动电机的运行状态。 3.2.1 开关量清洗 从SIS系统导出的原数据包含大量描述一次风机部件状态、运行模式和系统安全警报的开关量,通过此类离散型数据可以监控一次风机及其附属系统的工作状态,实现系统安全的直观反馈。但对于连续型状态数据的预测,离散型开关量会增加训练数据的冗余,降低模型的精度和效率,因此预处理需要剔除开关量特征。剔除开关量特征后的一次风机特征参数见表1。 表1 一次风机特征参数 3.2.2 异常值清洗 在实际生产中,一次风机需要进行故障检修或定期点巡检,因此数据集会记录一次风机停机时的各测点数据,此类数据不属于本文关注的一次风机正常运行状态,不能用于建立风机状态预测模型,应视为异常值数据,对其进行清洗。以7号机组一次风机A为例,选取一次风机电流作为判断其停机的标准,清洗数据集中的停机数据和显著异常值点。 (1) 停机数据清理。 在电厂实际生产中,机组的大小检修和临停及单台风机的临时检修对应的数据均会被记录为无用的样本数据。一次风机电流为零的样本点被判定为停机状态点,应删除该类少数样本点。 (2) 显著异常值点数据清理。 对一次风机电流参数的剩余样本数据进行方差分析,对于超限的噪音数据,采用分箱中位数法进行平滑处理。 数据清洗前后各采样点的一次风机电流如图4所示。 (a) 数据清洗前 计算表1中33个特征参数的相关系数,其热力图如图5所示,其中x1,x2,…,x33为表1中列出的33个特征参数。热力图方块的颜色越深,相关系数绝对值越大,代表2个变量之间的相关性越强。 图5 相关系数热力图 根据文献[3],一次风机运行时的气体温度变化、进风管道堵塞或破裂、叶轮磨损和转速故障会引起一次风机入口风量及出口压力的异常变化,若不及时处理会影响锅炉燃烧,进而影响整个电厂机组发电。一次风机通过压力、流量和振动等相关参数表征的故障可达到总故障数的80%。以出口压力作为状态特征预测量,构建与其有关的一次风机故障状态预测模型,从而控制风机状态,实现对风机故障的预警。 根据式(14)计算一次风机入口、出口压力与其他特征参数的相关系数,各维度相关系数大于0.5的特征参数见表2。 表2 出口压力与其余特征参数的相关系数 经过相关性分析,选取与出口压力具有高相关性的特征参数,将原有的33个特征参数减至10个,实现了数据降维。最终选取这10个特征参数作为一次风机状态预测模型的输入参数,建立预测模型。 本文模型的输入变量较多且量纲不统一,需将数据进行归一化处理。其表达式如下: (17) 采用均方根误差(CRMSE)、平均绝对误差(CMAE)和平均绝对百分比误差(CMAPE)作为预测模型精度的测试标准,这些数值越小,代表模型的预测精度越高。采用均方误差(CMSE)作为适应度函数,其表达式[14,16]如下: (18) (19) (20) (21) 在Windows10系统python3.9环境下对上述方法进行计算分析。将2021年1月1日至12月31日共4×8 416×10个数据组成数据集,随机挑选70%的样本数据作为训练集,剩余30%的样本数据作为测试集,输入一次风机状态预测模型中进行建模预测。将2个超参数的网格寻优范围设置为0~30,步长设置为5进行搜索,计算网格点的计算精度,获取2个超参数的全局优化初始值。将网格寻优的结果作为天牛初始质心输入IBAS模型中进行二次参数寻优,获取全局最优超参数。改进前后的适应度值迭代收敛曲线如图6所示,具体运行参数见表3。 图6 寻优迭代曲线对比 表3 算法运行参数对比 由表3可知,与BAS相比,IBAS提高了算力利用率,增加了有效迭代次数,收敛速度更快,收敛精度更高。 IBAS的迭代历程如图7所示。图中上方色块部分为网格搜索寻优的结果,获取了2个超参数的全局优化初始值,网格寻优的结果作为IBAS的初始天牛质心,进行进一步搜索寻优;线条为天牛爬行轨迹,即IBAS的寻优轨迹。 图7 改进天牛须搜索算法的迭代历程 使用最优超参数构建完整的一次风机状态预测模型,最终预测结果如图8所示。为方便观察规律,放大了局部曲线。 (a) 7号机组一次风机A局部 计算本文所提模型在实测数据集下的评价指标,并将其与LSSVM模型和BP网络模型在同一数据集下的评价指标进行对比,结果见表4。 表4 模型预测精度对比 经过4组数据集的建模测试,IBAS-LSSVM模型的CRMSE、CMAE和CMAPE均低于其他2种模型。由图8可知,所提模型的拟合效果优于BP网络模型,与实际值最为接近。所提模型的平均绝对百分比误差为2.53%,相比LSSVM模型降低了2.41%,相比BP网络模型降低了0.77%。所提模型在一次风机出口压力的预测上平均精确度达到97.47%。综上所述,所提一次风机状态预测模型预测精度高,且收敛速度快,可满足一次风机状态预测及故障预警工程实践的需求。 (1) 提出基于IBAS优化的LSSVM一次风机状态预测模型。利用IBAS参数少、计算量少的优点,对LSSVM模型中的超参数进行高效率智能寻优,提高了模型精度,降低了一次风机状态预测的误差。 (2) 基于“系统+部件”的思想,构建一次风机多维特征体系,挖掘同维度下的特征耦合性规律进行数据降维,减少模型冗余,提高了预测的效率。 (3) 针对BAS运行时会出现局部最优的情况,应用网格化搜索算法确定2个超参数的全局初始值;重新利用天牛左右须的位置坐标和适应度值,并采用混合步长代替原有的递减步长。仿真结果表明,与BAS相比,IBAS提高了算力利用率,增加了有效迭代次数,收敛速度更快、收敛精度更高。 (4) 算例分析结果表明,所提模型在CMAPE上比LSSVM模型降低了2.41%,比BP网络模型降低了0.77%,在一次风机出口压力的预测上平均精确度达到97.47%,验证了本文模型的优越性。3 算例分析
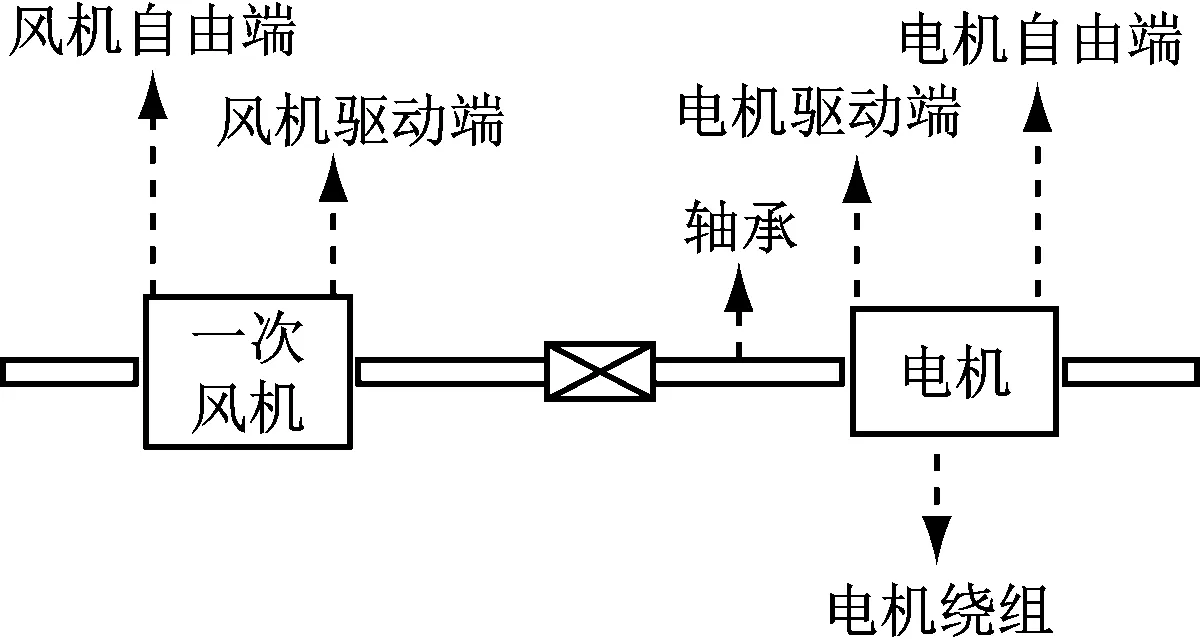
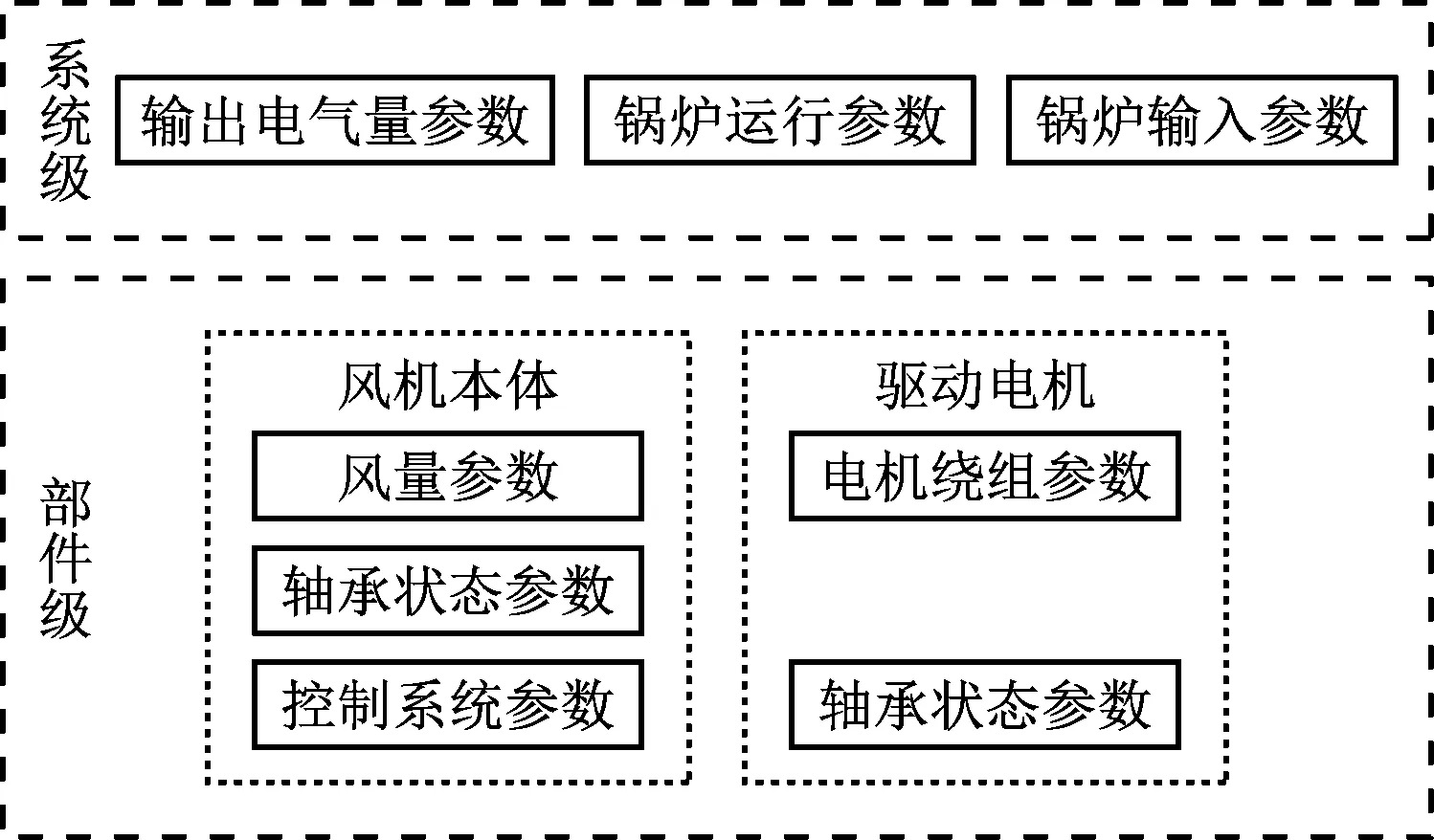
3.1 基于“系统+部件”思想的多维特征体系构建
3.2 数据预处理
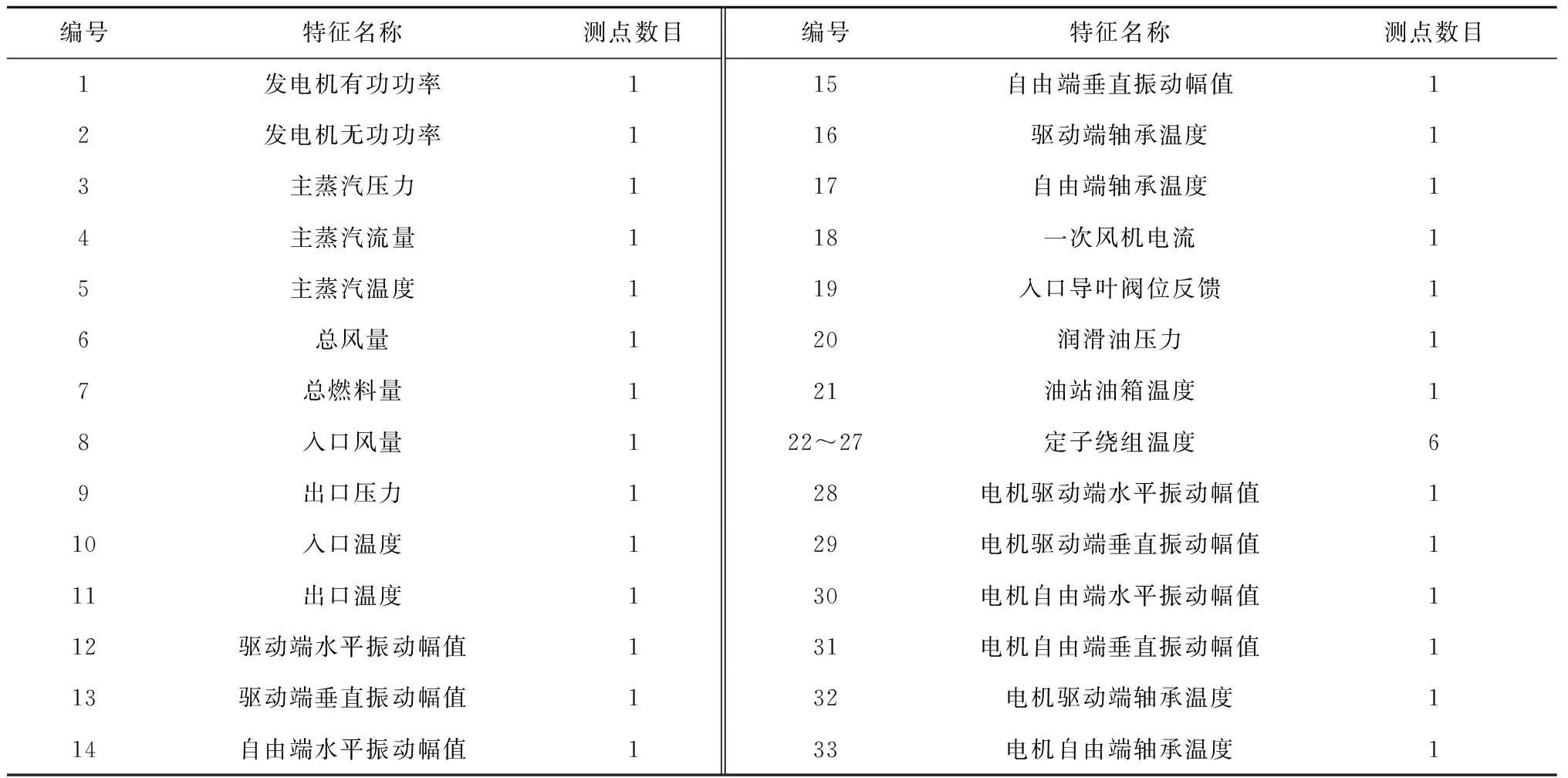
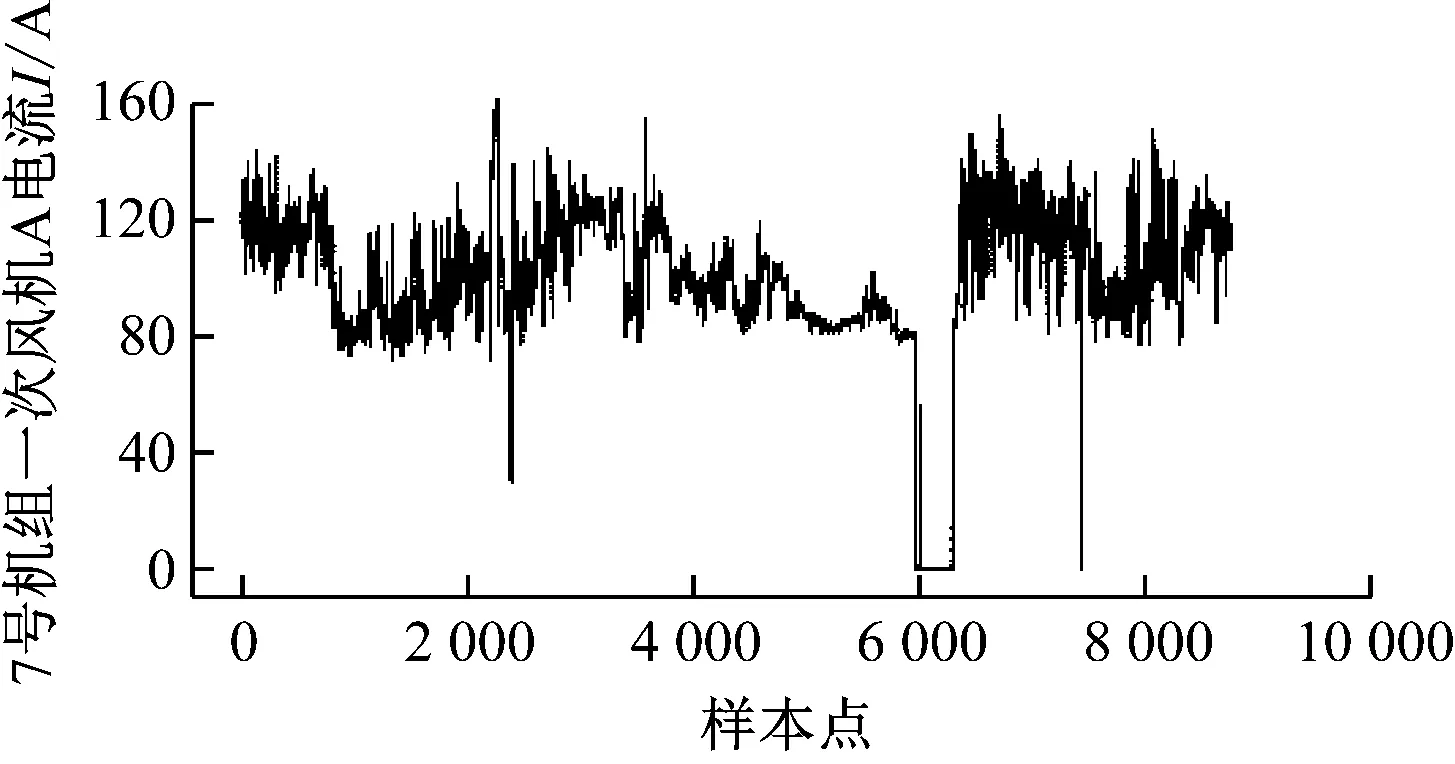
3.3 特征选择

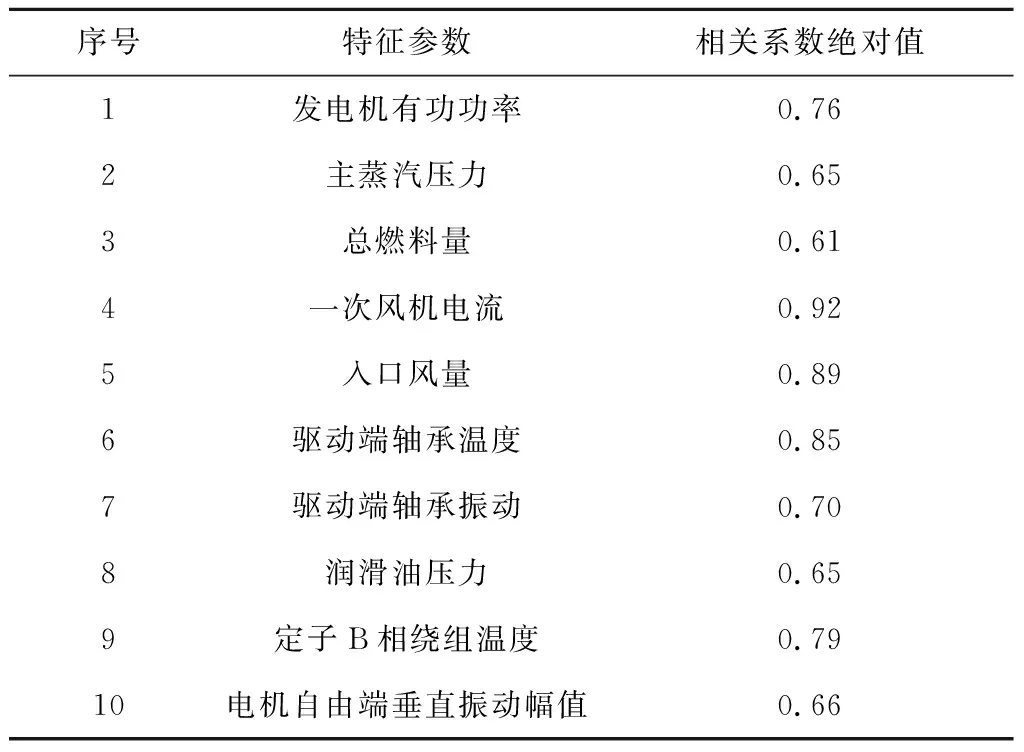
3.4 归一化处理与模型评价指标

3.5 训练结果分析

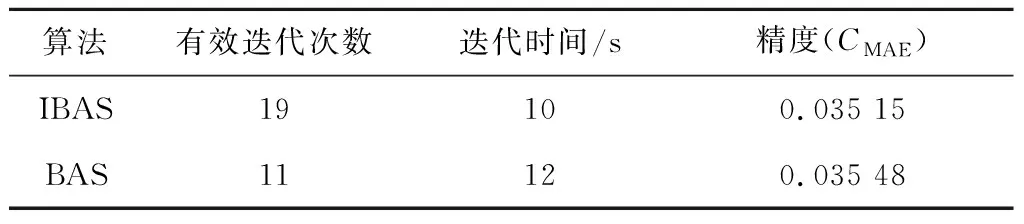

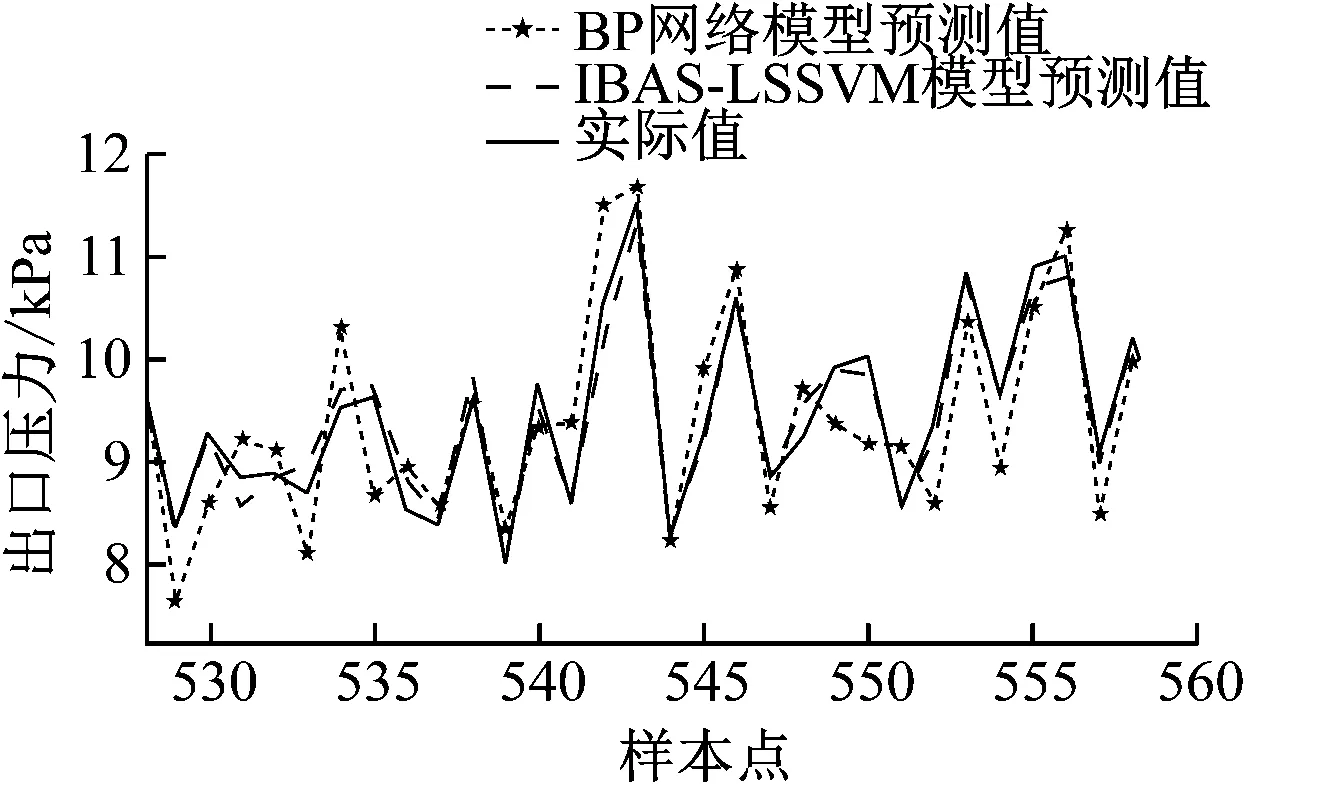
4 结 论

