海上漂浮式风电场高比例并网一次调频控制策略研究
宋子秋, 余照国, 胡 阳, 刘吉臻
(华北电力大学 控制与计算机工程学院,北京 102206)
随着海上风电在全球能源转型背景下的迅猛发展,我国海上风电装机并网数量不断增加,2021年新增装机容量达16.9 GW,约占全球新增装机总量的50%[1]。我国海上风能资源禀赋丰裕,但目前已开发利用的近海风能远小于深远海域蕴含的风能[2-3]。围绕“碳达峰”、“碳中和”战略目标[4],构建以新能源为主体的新型电力系统,远海漂浮式风电高比例并网成为未来电力系统发展的必然结果。
由于风能资源的波动性、间歇性和随机性,大规模风电并网会破坏电力系统有功功率与负荷之间的平衡[5],引发电网频率的波动,威胁供电系统的安全经济运行。海上漂浮式风电与陆上风电存在明显的差异,复杂的海上风浪环境使得漂浮式风电机组在现有控制策略下很难保持参数稳定和输出功率平滑[6-7],缺乏惯量支撑和一次调频能力,其大规模并网后给电网造成更为严重的冲击[8]。海上漂浮式风电受风、浪载荷的影响,漂浮平台和风机塔体会发生位移和俯仰运动[9-11],导致风电场输出功率在期望值附近波动,并网后将引起电力系统频率的变化。随着电力系统区域互联程度的增加和漂浮式风电渗透率的提高,电网频率波动的问题将会愈发严重,因此需要为其配备频率响应系统,参与一次调频。
目前,风电机组参与电力系统一次调频的研究主要涉及陆上风电和近海固定桩风电,主要方法包括转子动能控制、减载运行控制及储能参与调频控制。转子动能控制可分为虚拟惯量控制和下垂控制。Morren等[12]最早提出虚拟惯量控制的思路,通过附加频率控制单元计算风力机输出功率参考值,使风力机具备惯性响应能力。Miller等[13]在有功功率控制中引入系统频率偏差信号,使风电机组具备频率-功率下垂特性。文献[14]和文献[15]将风力机运行区间划分为低、中和高风速区域,不同运行区间采用不同优化指标整定下垂系数,实现风力机最优下垂特性。一般情况下,由于风电机组转子动能有限,转子动能控制调频只能维持较短时间,且在风力机退出调频后的转速恢复阶段,其输出功率大幅减少,可能会导致系统频率的二次跌落。减载运行控制主要分为转子超速控制和变桨距控制。张昭遂等[16]分析了转子超速控制和变桨距控制的局限性,提出将两者相结合的协调控制方法,在一定程度上改善了风电机组的调频特性,但同时降低了风能转化效率。储能系统具有快速响应和灵活控制的能力,是在高风电渗透率下维持电力系统频率稳定性的重要手段。刘忠仁等[17]利用电池储能系统缓解了风电并网引起的电力系统频率波动,进一步分析了储能电池容量对区域电力系统频率控制的影响。颜湘武等[18]利用超级电容组模块协调风电机组一次调频,在改善机组惯性响应性能的同时,提高了风力机运行的稳定性和经济性。
上述研究均对风力机参与电力系统一次调频领域有一定的贡献,但在此基础上,该领域仍应在以下几个方面需要加强研究:(1)含漂浮式风电场的混合电力系统频率特性;(2)高比例漂浮式风电场并网对电力系统定性和定量的影响;(3)在高比例漂浮式风电场并网背景下的一次调频控制策略。为此,笔者首先建立了含漂浮式风电场和电池储能系统的风-火-储混合电力系统一次调频模型,为对含漂浮式风电场或含高比例漂浮式风电场电力系统的频率特性的定量和定性研究提供了理论基础;然后,提出储能电池协调高比例漂浮式海上风电场的一次调频控制策略;最后,以Matlab/Simulink软件和FAST风电仿真软件为基础,以半潜漂浮式风电场为对象,搭建仿真实验平台,分析波浪载荷对电力系统性能的影响,并在阶跃负荷和随机负荷2种场景下,仿真对比了转子动能与超速减载联合一次调频控制策略和基于电池储能的海上风电机组调频策略,以验证所提方法的有效性。
1 含漂浮式风电场的混合电力系统一次调频模型
1.1 漂浮式风电场一次调频模型
与陆上和近海风力机相比,漂浮式海上风力机的运行环境更加复杂恶劣,在风、浪载荷作用下,海上风力机的漂浮基础平台和机身塔架会发生横向摇动和纵向俯仰运动,造成机组输出功率持续波动。以美国国家可再生能源实验室(NREL)开发的5 MW半潜漂浮式海上风电机组为风电场的单机对象,半潜漂浮式风力机模型和风、浪等环境载荷模型的建模采用FAST风电仿真软件中相关模型,其参数参考文献[19]。
为实现变速恒频漂浮式风电机组参与电力系统调频,附加频率控制十分必要,通过为机组配备频率响应单元,确保风电机组的出力响应电网频率变化。频率响应单元采用虚拟惯性控制和下垂控制的综合控制方式,根据漂浮式海上风电场并网频率偏差计算风力机的额外有功功率参考信号,表达式为:
(1)
式中:KH和KD分别为虚拟惯性控制和下垂控制系数,KH与漂浮式风电机组的惯性时间常数、额定容量和发电机转速标幺值有关,KD与漂浮式风电机组的额定功率和调差系数有关,这2个系数的整定方法见文献[20]和文献[21];Δf*为漂浮式海上风电场并网频率变化量,Hz;ΔP*为风力机的额外有功功率参考信号,W;t为时间,s。

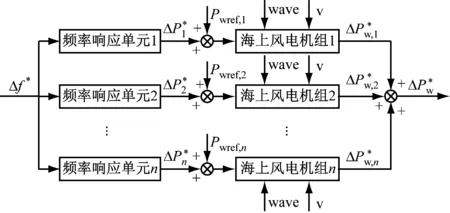
图1 漂浮式风电场一次调频模型
电网调度中心给出的海上风电场输出功率的参考值为Pwref,表达式为:
Pwref=Pwref,1+Pwref,2+…+Pwref,n
(2)
正常运行时,电场调度中心根据海上风电机组的额定功率按比例分配初始功率Pwref,i,即
(3)
式中:Pmax,i为第i台海上漂浮式风电机组的额定功率,W。

(4)
式中:μi为第i台海上漂浮式风电机组的发电机效率;Tg,i为发电机电磁转矩,N·m;ωg,i为发电机转速,rad/s。
发电机电磁转矩和转速的动态方程及控制方式可以参考文献[22]。
1.2 电池储能系统一次调频模型
电池储能系统主要包括储能单元、能量管理系统和功率转换系统,其中变换器和储能电池最关键,其等效电路如图2所示。其中:Et为电网相电压,Ed为变换器端电压,Eb为电池端电压,Ebt为电池过电压,Eoc为电池开路电压,单位均为V;Rc为连接电阻,Rt为过电压电阻,Rb为内部电阻,Rp为放电电阻,单位均为Ω;Cbt为过电压电容,Cbp为放电电容,单位均为F;α为变换器触发角,(°);Xco为变换器电感的阻抗,Ω;Ib为电池储能系统输入电流,Ibc为流经电池过电压电容的电流,单位均为A。
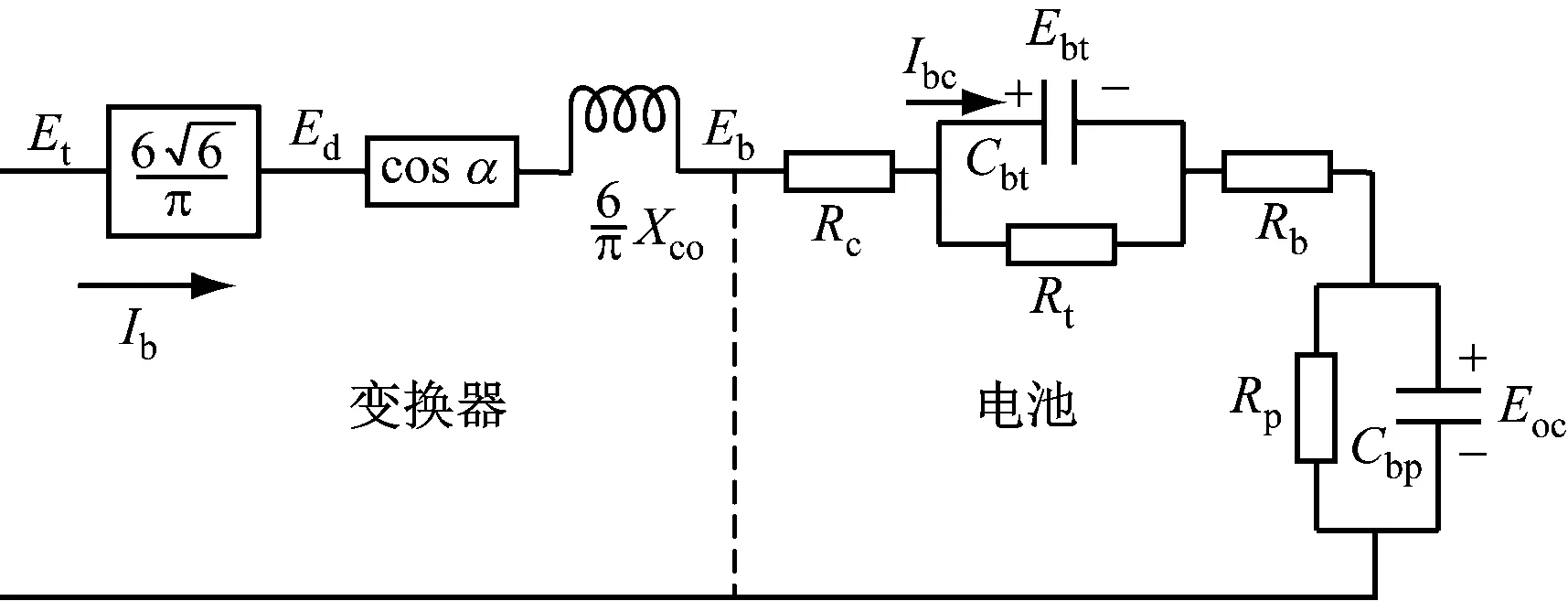
图2 电池储能系统等效电路
忽略无功功率和电压对电力系统频率的影响,储能电池充放电的有功功率Pb为:
(5)
式中:Ec为储能电池电压,V ;Ed0为变换器空载时最大的直流电压,V。
将式(2)线性化,得到如下表达式:
ΔPb=Ec0ΔIb+Ib0ΔEc
(6)
式中:ΔPb为储能电池的有功功率,W;Ib0和ΔIb分别为线性点处电池储能系统的稳态输入电流和输入电流变化量,A;Ec0、ΔEc分别为线性点处储能电池稳态电压及其变化量,V。
变换器通过调节晶闸管触发角α来使电池处于恒功率充放电模式,因此将ΔEc分为2部分:一部分补偿因输入电流变化产生的偏差ΔEp,另一部分补偿系统频率扰动引起的偏差ΔEd,得到表达式如下:
ΔPb=Ec0ΔIb+Ib0ΔEp+Ib0ΔEd=Ib0ΔEd
(7)
通过测量电网频率反馈信号(即频率变化量)Δf可以计算得出ΔEd:
(8)
式中:Km为测量回路控制增益;Tm为测量装置的时间常数,s;s为拉普拉斯算子。
引入符号函数,储能电池的充放电功率表达式为:
(9)
当sgn=1时,ΔPb>0,储能电池充电;当sgn=-1时,ΔPb<0,储能电池放电。
另一方面,通过分析充放电过程中电池内部电容与电流之间的关系,得出:
(10)
式中:Xbt为储能电池充电阻抗,Ω;Xbp为储能电池放电阻抗,Ω;ΔEbt为储能电池过电压电容电压变化量,V;ΔEb和ΔEoc分别为储能电池端电压和开路电压的变化量,V。
对式(7)进行拉普拉斯变换,电池储能系统一次调频模型结构如图3所示。其中:Tbt为电池充电等效时间常数,s;Tbp为电池放电等效时间常数,s。
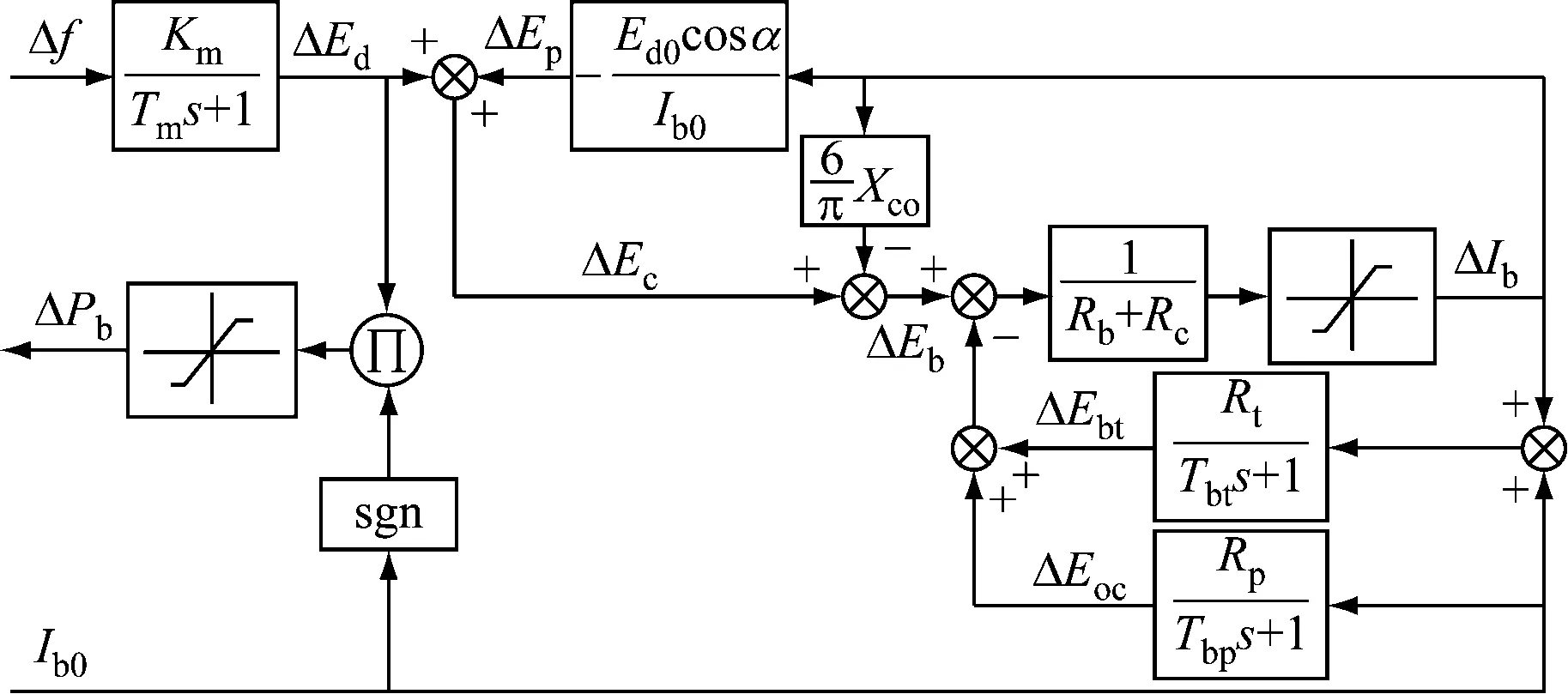
图3 电池储能系统一次调频模型
1.3 火电机组一次调频模型
火电机组一次调频模型主要包括调速器模型和汽轮机模型,调速器模型关系式如下:
(11)
非再热型汽轮机模型关系式如下:
(12)
再热型汽轮机模型关系式如下:
(13)
1.4 风-火-储混合电力系统一次调频模型
根据电力系统负荷频率特性,可以得到如下表达式:
(14)
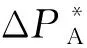
利用电池储能系统协调海上风电机组参与一次调频,为所有并网的海上风电机组装配储能电池,合并储能电池输出功率与海上风电机组输出功率。对于含m台火电机组、风电场含n台海上风电机组的电力系统,需满足:
(15)
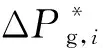
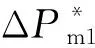
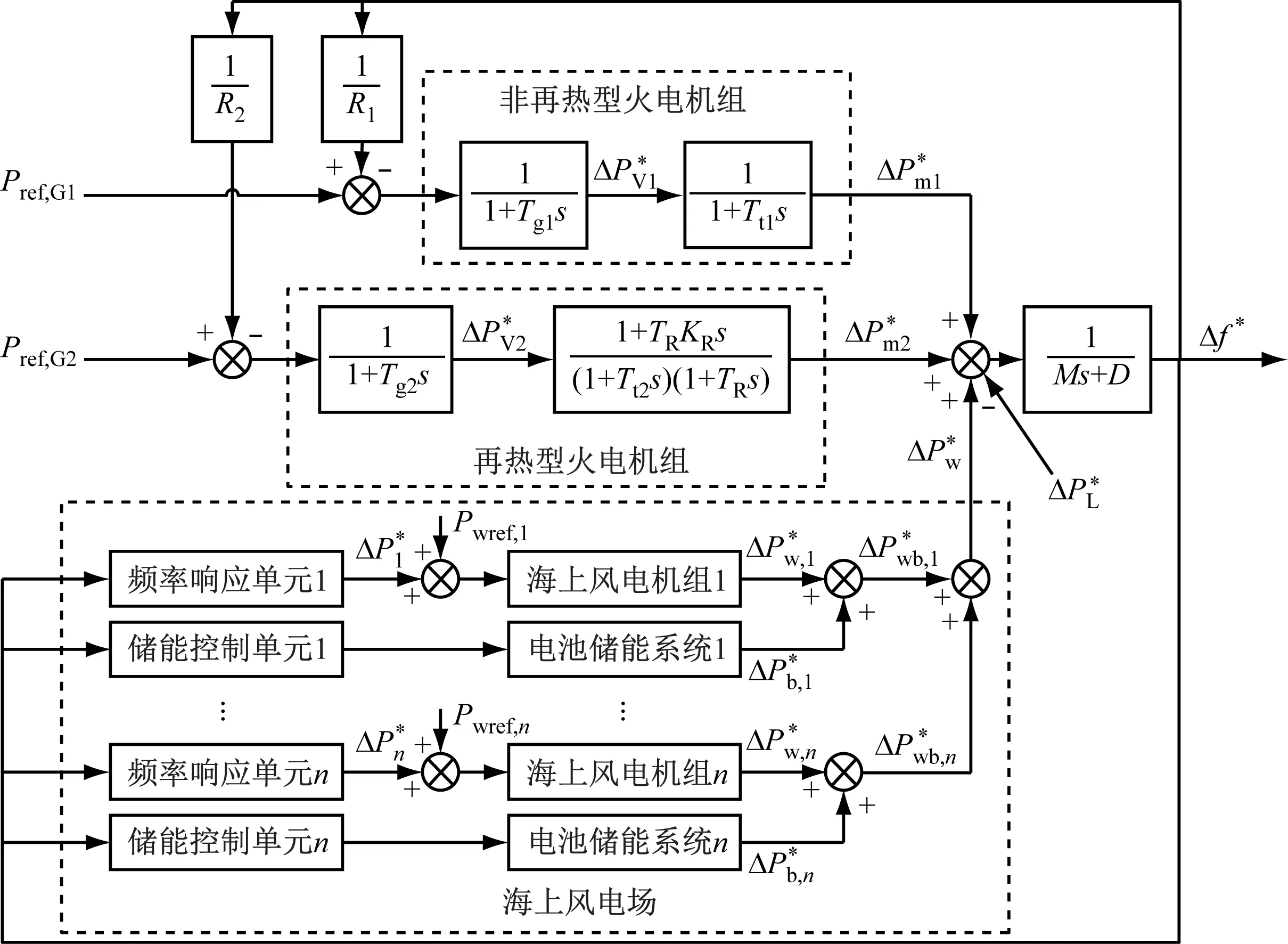
图4 风-储-火混合电力系统一次调频模型
2 基于电池储能的海上风电场一次调频策略
2.1 电池储能系统一次调频控制策略
电池储能系统一次调频运行特性如图5所示。其中:Δfu和Δfd分别为调频死区的上限和下限,Hz,一般分别取值0.03 Hz和-0.03 Hz;ΔfU和ΔfD分别为电池储能可调频的上限和下限,Hz。电力系统正常运行时,对于特定范围内的频率小幅扰动,无需调节,因此对储能电池设置一次调频死区环节。
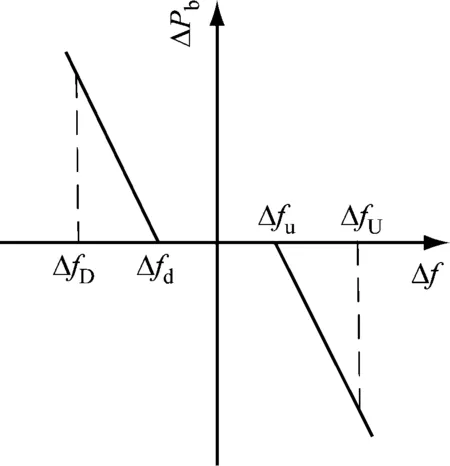
图5 电池储能系统一次调频运行特性
储能电池的充放电状态与电池的荷电状态(SOC)有关,且储能电池的充放电动作深度存在限度。电池荷电状态Sc可定义为剩余电量与额定容量之比,即
(16)
式中:E0和EN为储能电池的初始电量和额定容量,J;tc为电池充放电时间,s;Sc0为初始荷电状态。
为了保证储能电池的稳定运行,延长其使用寿命,要求电池不能过充和过放,规定储能电池SOC的约束范围为:
Sc,min≤Sc≤Sc,max
(17)
式中:Sc,min和Sc,max分别为储能电池SOC的下限和上限,一般取20%~100%。
在研究电力系统频率偏差与电池储能系统输出功率的关系时,可以将电池储能系统等效为一阶惯性环节[23],即
(18)
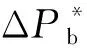
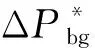
(19)
式中:MB为虚拟惯性控制增益。
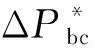
(20)
式中:KB为下垂控制增益。
2.2 漂浮式风电机组一次调频控制策略
漂浮式风电机组主要使用转子动能与超速减载联合一次调频控制策略。当电力系统频率下降时,利用风电机组虚拟惯量将转子动能快速转化为电磁功率;惯性响应后,超速减载控制开始作用,使风电机组运行保持在原减载运行曲线之上,从而增大机组输出功率,参与系统一次调频;当系统频率稳定在允许范围之内时,超速减载控制停止作用,此时风电机组以新的减载率稳定运行。
采用风电机组转子动能控制调频,需为机组配备附加频率响应单元,将电力系统频率偏差转化为风电机组的额外有功功率参考信号,利用风电机组虚拟惯量实现转子动能与有功功率之间的短暂性交换。正常运行时,风电机组转子中蕴含的动能可表示为:
(21)
式中:Ew为风电机组转子动能,J;Jw为风电机组等效惯量,kg·m2;ωr为风电机组转速,rad/s。
风电机组通过释放转子动能获得的电磁功率Pw为:

(22)
在转子超速控制减载运行下,风电机组的输出功率表达式为:
(23)
式中:Pmax为风电机组最大机械功率,W;Pd、ΔPd分别为风电机组超速减载运行时的输出功率及其变化量,W;Cp,d(λ,β)为超速减载运行下的风能利用系数;d为减载率;ρ为空气密度,kg/m3;v为风速,m/s;rw为风轮半径,m;Cp,max(λopt,β)为风电机组最大风能利用系数。
2.3 一次调频控制策略总体设计

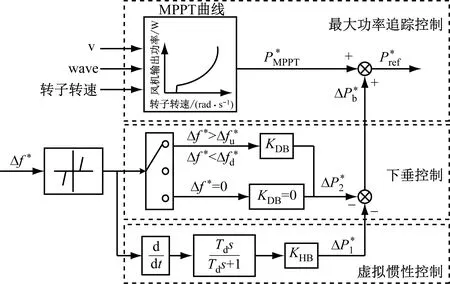
图6 基于电池储能的海上风电机组一次调频控制结构框图
为了满足电力系统一次调频的要求,避免储能电池发生过充和过放,在每次充放电动作前,首先判断当前SOC是否在正常运行范围内;在电池的充放电过程中,当SOC达到上限或下限时,电池主动退出调频。基于电池储能的海上风电机组一次调频控制策略控制逻辑如图7所示。
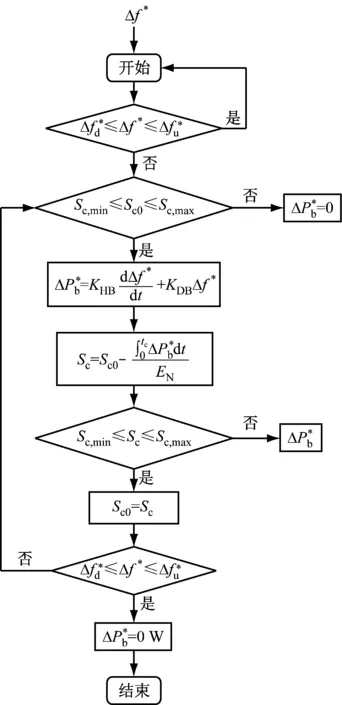
图7 基于电池储能的海上风电机组一次调频控制逻辑
当SOC满足储能电池正常运行的范围要求时,在一次调频过程中,电池储能系统输出功率与电力系统频率变化量之间的关系如下:
(24)
3 结果与分析
3.1 实验参数设置
以NREL 5 MW半潜漂浮式海上风电机组组成的高比例海上风电场作为研究对象,采用FAST风电仿真软件,在Matlab/Simulink仿真平台中搭建混合电力系统一次调频模型,设计并搭载储能和海上风电机组一次调频控制器,仿真验证了波浪特性参数对电力系统性能的影响,以及所提的转子动能与超速减载联合一次调频控制策略和基于储能电池的海上风电机组一次调频控制策略的有效性。
搭建的电力系统结构如图8所示。系统电源仅包含同步发电机组和漂浮式海上风电场,系统负荷基准为1 000 MW,同步发电机组装机容量为1 600 MW,系统含5 MW半潜漂浮式海上风电机组100台,装机容量共500 MW,同时给每台漂浮式海上风电机组配备容量为1 500 kW×60 s的电池储能系统。设定漂浮式海上风电机组的输入风速为8 m/s,正弦波浪载荷的浪高为2 m,风电机组初始减载率为20%,虚拟惯性控制系数和下垂控制系数分别为10.08和10.00,高通滤波器的时间常数设置为8 s,储能电池的初始SOC为70%。
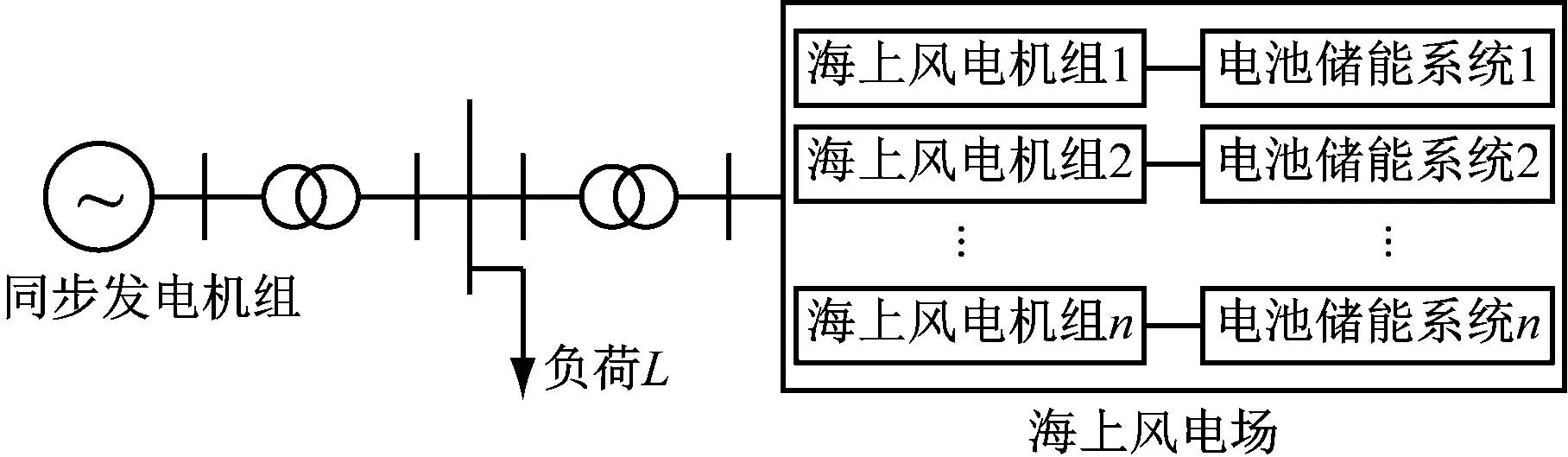
图8 电力系统结构仿真示意图
3.2 波浪载荷影响
在额定风速以下和额定风速以上时,漂浮式风电场在有效浪高分别为1 m、3 m和5 m的正弦波浪下,对海上风电场并网频率的变化动态进行仿真。仿真结果如图9和表1、表2所示,其中Max、MAE和SD分别为频率变化量的最大值、平均绝对误差和标准差,以下各参数均以标幺值来表示。
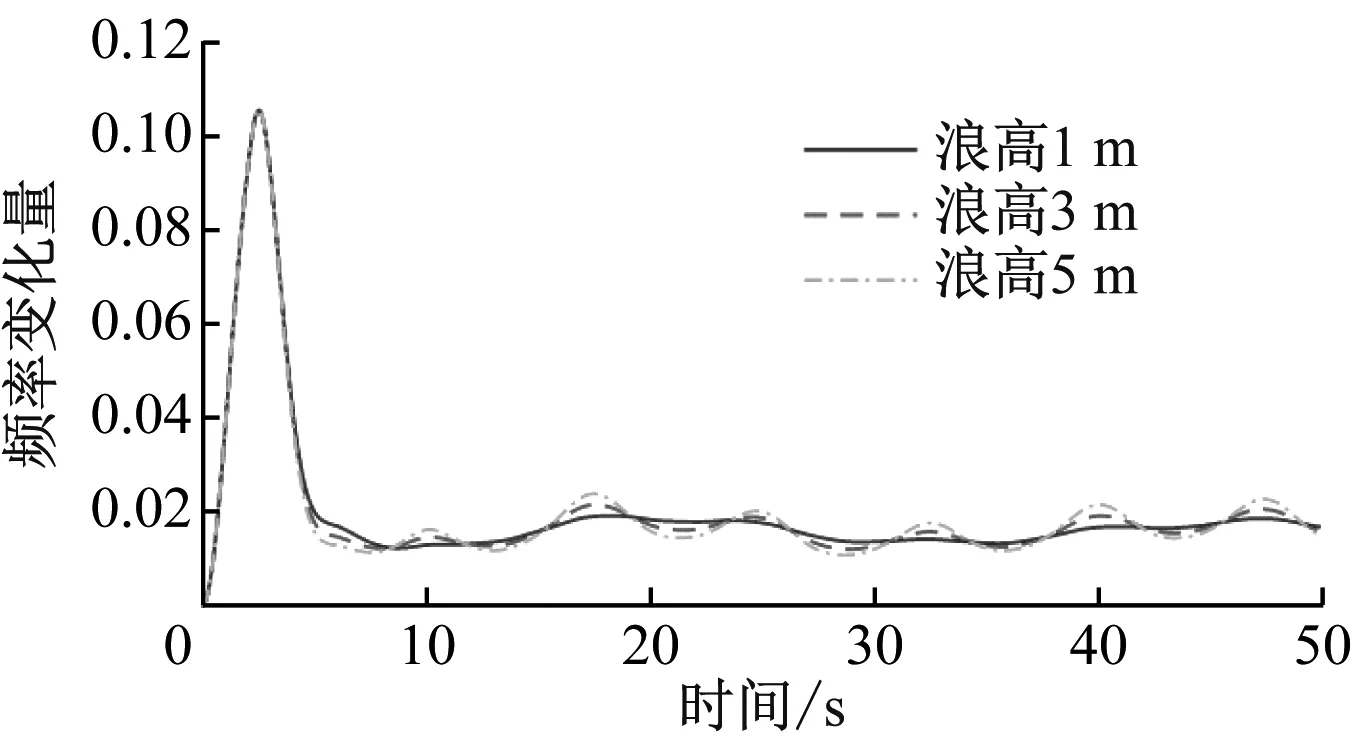
图9 不同浪高正弦波浪载荷下海上风电场并网频率变化量
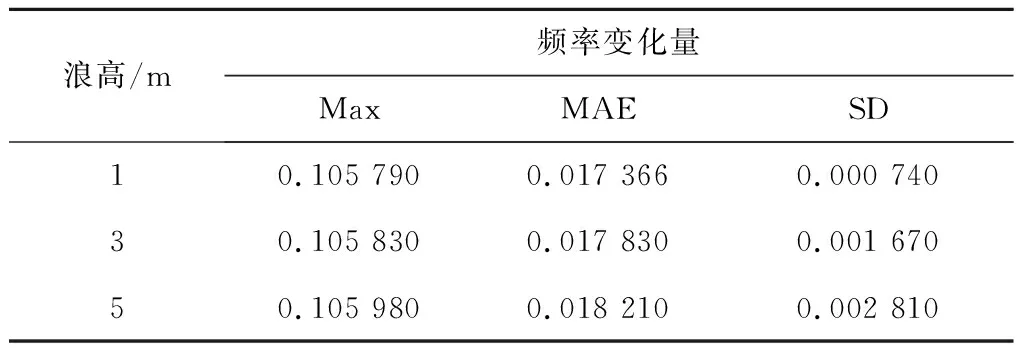
表1 海上风电场并网频率对浪高的响应(8 m/s)

表2 海上风电场并网频率对浪高的响应(15 m/s)
额定风速以下,当输入稳态风速为8 m/s时,在3种不同浪高正弦波浪载荷下,海上风电场并网引起的电力系统频率偏差大体一致,海上风电场并网频率变化量的Max和MAE均约为0.106和0.018,但海上风电场并网频率上升的幅值随着波高的增加呈微弱增大的趋势。在浪高为5 m的正弦波浪载荷下,海上风电场并网频率变化量的SD最大约为0.003,与浪高为1 m时相比增大了279.7%。
额定风速以上,当输入稳态风速为15 m/s时,在3种不同浪高正弦波浪载荷下,海上风电场并网频率变化量的Max和MAE均约为0.147和0.051。在浪高为5 m的正弦波浪载荷下,海上风电场并网频率变化量的SD约为0.003,与浪高为1 m时相比增大了229.9%。因此,正弦波浪载荷浪高的增加对海上风电场并网引起电力系统频率偏差幅值的影响不大,但会加剧电力系统频率的波动。
3.3 阶跃负荷情景
初始时刻电力系统正常运行,在10 s时负荷突增0.35,电力系统频率变化量、电源输出功率和储能电池输出功率如图10所示。
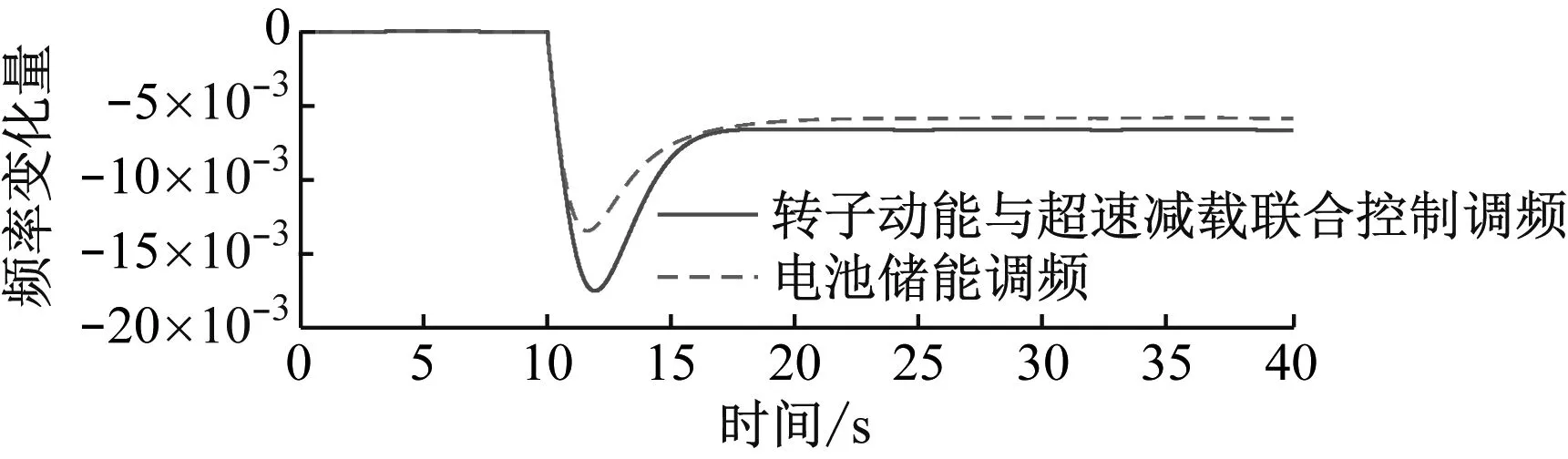
(a) 频率变化量
从电力系统频率变化量曲线可知,在电池储能调频下,与转子动能与超速减载的联合控制调频相比,电力系统一次调频的性能较优,电力系统频率变化量的最大偏差为-0.013,稳态频率偏差为-0.005 8,分别减小了22.4%和12.2%,同时电池储能调频的响应速度也明显更快。
从储能电池输出功率曲线可知,当负荷突增0.35时,电池输出功率为正,电池放电,相当于电力系统中的电源,其最大输出功率为0.128,一次调频后电池的稳态输出功率为0.052。
从火电机组输出功率变化量曲线可知,因为储能电池放电,电池储能调频下火电机组输出功率增量减小,与转子动能与超速减载的联合控制调频相比,其输出功率减少了24.9%。
3.4 随机负荷情景
为了更贴近现实中负荷变化的场景,当负荷连续随机变化时,对电池储能调频控制下的电力系统一次调频过程进行了仿真。当负荷发生连续变化的随机扰动时,电力系统频率变化量、电源输出功率和储能电池输出功率如图11所示。
由图11可知,在随机负荷扰动下,一次调频过程中电力系统频率发生剧烈的振荡波动。与转子动能与超速减载联合控制调频相比,电池储能调频具有明显的优越性,可以有效地减小电力系统频率的变化幅值和波动程度,改善了电力系统一次调频性能。
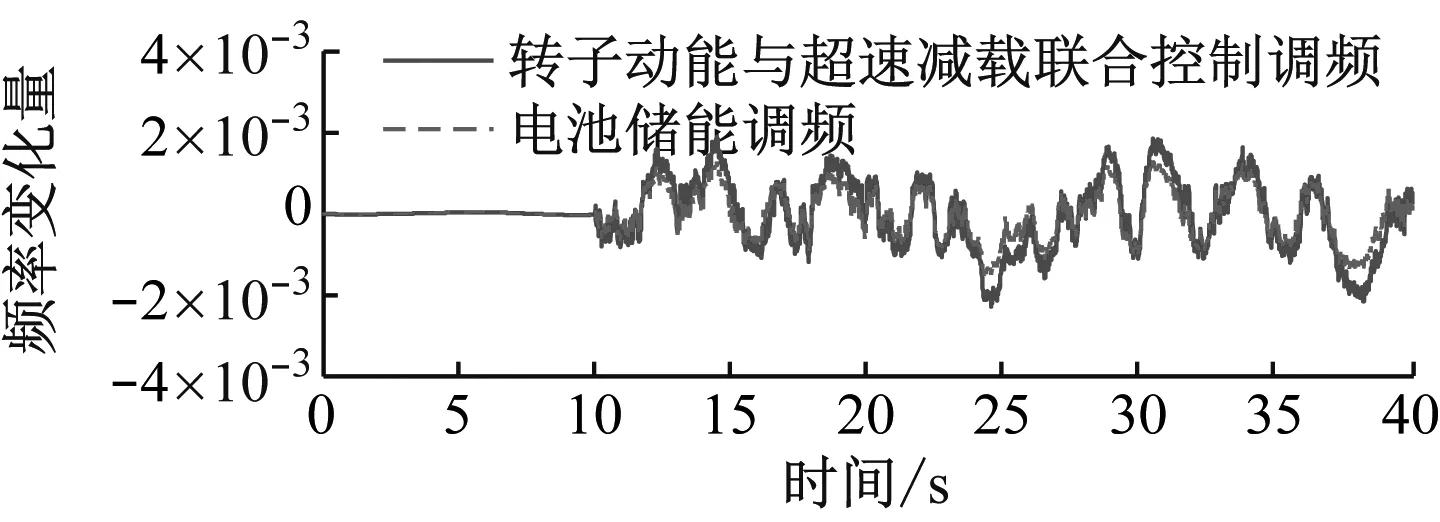
(a) 频率变化量
从储能电池输出功率曲线可知,在随机负荷扰动下,一次调频过程中储能电池输出功率可正可负,储能电池能快速、双向地吞吐功率,响应电力系统频率的变化,且电池输出功率与系统频率偏差呈负相关。电力系统频率升高,电池输出功率为负,迅速吸收系统有功功率充电;电力系统频率下降,电池输出功率为正,迅速输出有功功率放电;当系统频率偏差在调频死区范围之内时,电池不作任何响应。
从火电机组输出功率变化量来看,电池储能调频时火电机组输出功率变化量较小,有利于减轻火电机组快速变负荷的压力,降低机组运行成本。
4 结 论
(1) 建立含漂浮式风电场的风-储-火混合电力系统一次调频模型,可以准确模拟高比例漂浮式风力机渗透下电力系统的频率特性。
(2) 所提电池储能协调漂浮式风电场一次调频控制策略,可有效减小阶跃负荷和随机负荷场景下电力系统频率的变化幅值和波动程度,并提高调频响应速度。
(3) 电池储能参与一次调频可以有效减轻火电机组快速变负荷的压力,并使漂浮式海上风电机组的输出功率更加均匀。

