书画时序感采集系统设计*

律睿慜， 邢红姹， 梅莉琳， 晏 涛

(江南大学 人工智能与计算机学院，江苏 无锡 214122)

0 引 言

如今美学研究的前沿中，神经美学是一个重要分支，具身模仿是其中的重要研究主题[1]。它描述了一种关于审美心理的现象，即观赏者可以从静态视觉作品中感受到运动感，观者不仅可以回溯运笔动作，还能将其按照一定的时序衔接起来，书法理论家陈振濂将其称之为“时间性”，并认为这种从结果找过程的审美方式是书法独有的，体现了书法艺术最深刻的美学价值。本文设计了一个时序感采集系统，并基于马尔科夫链的熵率对时序感进行了度量[2]，对不同风格作品的时序感作了比较，发现传统书法具有最高的时序感，且不同风格的作品具有各不相同的时序感。

1 总体方案设计

本文参考以往对书画审美问卷的基本形式[3,4]，并针对“时序感”的特性，引入了“排序”题型进行时序感采集系统的设计，还引入了马尔科夫链模型，对实验数据进行分析。图1为研究框架。整个时序感采集系统是基于Windows操作系统，利用Mono工具衍生出的软件之一Unity进行编程设计的。实验支持跨平台测试，采用鼠标与系统进行交互的操作方式进行数据采集。

图1 研究框架

2 时序感采集实验

邀请1名书画方面的专业人士挑选作品，共选出6类，72幅作品，在本文分别用a-f代表，a为传统东方书法，b为抽象表现主义，c为日本现代书法，d为连续笔画，e为写意时尚插图，f为传统东方水墨。根据预实验以及查阅相关参考文献，考虑到复杂度可能会对时序感产生一定影响[5]，故本文实验先利用复杂度测试系统对72幅作品在1～100进行评分，并将评分转换为Z分数，再进行复杂度的比较。根据结果选出同一风格作品复杂度差异较大，不同风格复杂度相似的作品。如图2所示，为了方便展示对作品进行了不同程度的缩放。

图2 选出的34幅书画作品

2.1 “关键点”测试

在作品上任意选取两点，则人们有多大程度可以判断两点绘制的先后次序，这种判断方法的关键在于点的选取。本文实验在34幅作品上选取一些比较“关键”的点，用来代表整幅作品。

召集10名人员，男性5名，女性5名，都有绘画基础。每幅作品要标记一定数量重要的点。首先，在电脑上利用“关键点”测试系统进行测试。测试者可以利用鼠标在作品的任意位置进行标记，点击“删除”按钮可以进行已标记点的删除，点击“清除”可以删除所有已标记点，视野旁边的按钮可以对作品进行缩放和移动。随后，让测试者找出重要的线条，对线条的起点和终点以及具有明显变化的位置进行标记。最后，记录每幅作品标记点的数量和位置。分别将每幅作品的标记点经过K-Means聚类得到k个标记点，其中k根据具体作品确定[6]。聚类具体步骤：首先，选取k个初始聚类中心；然后，根据初始聚类中心把作品上所有标记点分为k类；最后，计算出聚类平均值，调整每个聚类中心，不断循环上述过程，直到聚类结果不再改变，其中,排除了距离和较远的孤立点。聚类结果作为代表该幅作品的“关键点”。

2.2 “时序感”测试

“时序感”测试系统包括3个方面，界面设计、获取鼠标数据和存储数据。界面设计采用按钮、文本框等实现作品以及关键点显示。获取鼠标数据是鼠标点击作品上的关键点触发Circle Collider 2D，根据触发顺序进行排序得到数据。存储数据如表1，每幅作品会记录关键点名称以及测试者的排列序号。

表1 作品的存储数据

召集了64名在读大学生，男生31名，女生33名，均不是艺术专业，右利手，年龄在19～22岁之间，视力或矫正视力正常，在电脑上进行实验。首先，进行测试，比如，点击第一个点时会有1生成，代表此点是排序的第一个点，且其颜色会从红色变成蓝色，再次点击以上操作会被取消。当所有点被标记后会出现“下一个”按钮，点击按钮即可显示下一幅作品，测试者继续测试。当34幅作品的关键点排序完成后，测试结束。每幅作品的排序数据形成一系列序列，参考已有文献对随机序列的处理，这里用马尔科夫链对排序序列建模并对其随机性进行度量[7]。

3 基于马尔科夫链的计算方法

3.1 马尔科夫链模型的建立

定理1若X(t)是随机过程，其中,t∈{0,1,…,T},x1,x2,x3,…,xt∈χ。且,对于随机过程X(t)而言，t时刻的取值仅与其前一个时刻t-1有关而与其他时刻无关。即满足条件Pr(Xt=xt|Xt-1=xt-1,…,X1=x1)=Pr(Xt=xt|Xt-1=xt-1)，此时称X(t)为马尔科夫链。满足该等式即符合马尔科夫性质。

本文选取一幅作品对其如何转换成马尔科夫链进行详细介绍。图3是已进行关键点标记的作品，首先对书画书写过程进行回溯，整个回溯过程会经过各个“关键点”，对每个关键点进行命名。图3是一个测试者的回溯过程，x1,x2,x3,x5,x6,x7,x8,x9,x4,x11,x14,x16,x15,x17,x18,x19,x13,x12,x10。

图3 该作品关键点及回溯过程

将此序列建模为一系列动作随着时间变换的序列[8]，把经过某个关键点当作进行某个动作，比如进行动作x3时只与它的上一个动作x2有关系，跟其他动作无关，故所形成的序列符合马尔科夫链的性质。若有q个测试者，将该幅作品测试的q个马尔科夫链连接到一起，本文称其为总马尔科夫链。总马尔科夫链可以看作一个由q幅图3组成的一幅大作品，每幅作品由q个人进行排序测试，每人测试一幅图3，得到序列同样符合马尔科夫性质。

3.2 以马尔科夫链的熵率度量时序感

本文用熵率量化书画的时序感，采用基于Lempel-Ziv压缩算法的方法来计算熵率对其时序的随机性进行度量。

(1)

式中 log2n/Li(χ)用作熵计算器，对长度为n的序列进行编码，n为同一幅作品所有测试者的动作变换连成序列的长度，计算在这个过程编码的平均位数。滑动窗口的熵率计算为

(2)

3.3 利用Stationary Bootstrap计算标准误差

对于有相关性的时间序列常用的抽样方法是块抽样，Stationary Bootstrap是块抽样的一种变体[10]。

块抽样是把序列分为不同的Block，在每个Block中数据的关联性就可以被保留下来。应用在序列长度为n的数据中，Moving Block Bootstrap把连续b个数据定义为一个Block，从序列第一个数值开始，Block每次前进一个值，共得到n-b+1个Block，再进行随机抽取。而在Stationary Bootstrap中Block长度是一个随机变量，长度概率满足几何分布。

这个方法的优点是给定原始观测序列，形成新序列是固定的。困难的地方是要确定参数的大小，在这里文献[7]采用p=H(χ)/log2n。仿真模拟生成1 000条序列计算标准误差，用以衡量熵率计算值的偏离程度。

3.4 实验结果

对34幅，6类书画进行分析，得到结果如下:

1)第一个方面如图4所示，除图4(a)外，同一风格内不同作品的熵率变化差异较大，每种风格的标准误差差异较小，每个作品的时序感都是可以被度量出来的;

图4 不同类型内作品熵率的大小以及标准误差

2)第二个方面如图5所示，对不同类型作品熵率平均值进行比较。熵率越小说明测试者排序越统一，回溯程度越高，作品的时序感越强；反之则说明测试者排序越分散，作品的时序感越弱。根据结果可得，a代表的传统书法时序感最强。由熵率平均值得出时序感强弱变化：a>c≈d>b≈e≈f，可以看出：不同作品的时序感有比较显著的差异，时序感可以作为书画分类的标准。

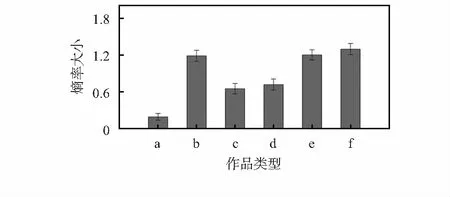
图5 不同类型作品熵率平均值及标准误差

4 结束语

提出了一种基于人主观感受的书画评价指标—时序感，基于本文设计的时序感采集系统对作品时序感进行测试并进行定量分析，得出了不同作品的时序感关系：传统书法最高；日本现代书法和连续笔画次之；抽象表现主义、写意时尚插图和传统水墨画最弱。此研究提出了新的书画分类标准并将技术应用于艺术领域进行测量，为以后研究书画提供参考依据，并有利于学科的交融，具有研究价值。