基于决策树算法的文科类科研人员数学知识模型需求研究

●吴俊杰

一、引言

现代科学一体化的趋势使得数学知识模型应用的领域更加广泛，数学知识模型不仅是处理自然科学的重要手段，也成为了文科类科研人员学习、科研中普遍需要的方法，其在处理文科类问题中已经得到了充分的运用。如查志杰等[1]根据现有具备一定代表性的教学质量评价指标，运用“遗传算法优化后的BP神经网络”建立了考察教学质量的综合评价模型对教学质量进行综合评估和排名，这一研究有助于教育工作者的反思和总结；杜德斌等[2]在研究法学中“城市犯罪的空间分布和过程”这一问题时，用数学中动态规划的方法建立了区位选择的微观模型来模拟罪犯在城市内选择犯罪区位的规律，这一方法的应用将极大提升对“不同区域犯罪”的针对性打击力度。续建宜等[3]在《历史研究中的数学方法——数量史学评介》中提出数学知识模型与历史学的结合越来越紧密，“数量史学”这门新学科的兴起正是两者结合的一个重要产物，该学科中一个重要部分就是制作各种数理模型来促进对历史现象与过程的数量化研究。而作为人工智能算法之一的决策树算法在文科类中的运用也愈加广泛。CART决策树算法是Breiman[4]于1984年提出的一种构建决策树的方法，该算法采用基尼分割系数作为属性选择的判别度量。易俗等[5]运用CART决策树算法构建了高校教师亚健康决策模型，有利于客观高效地对教师亚健康程度进行评估。蓝传锜等[6]首次把CART决策树算法应用在关键词抽取工作中，对网络新闻的数据信息进行了有效提取和开发。这些相关文献中对文科类科研人员数学知识模型需求的探究较少，而本文主要通过CART决策树算法探究了主修专业、科研所在城市、对数学量化方法普及性认可度等差异下的文科类科研人员对数学知识模型的个性化需求情况，并结合已有数据对文科类科研人员从“提供数学知识模型的科研辅助网站”中获益程度的期望进行了分析，综合上述结果为未来数学知识模型如何更好的辅助文科类科研人员提出了展望。

二、CART决策树算法

（一）CART决策树算法步骤

CART决策树算法是一种常用的非参数分类和回归方法，本文主要运用其中的分类方法，以下将介绍该方法中的选择特征、递归、剪枝三个重要步骤[7]。

1.选择特征。本文中所用的CART决策树使用基尼分割系数作为划分属性的判据,基尼分割系数数值越低则不纯度越低，特征越好，属性划分越有效。若整个训练样本集共包含n个属性，则基尼系数可以定义如下[5]：

其中Pt为决策属性值t在训练样本DX中的相对概率，如果集合DX中共有x条训练数据，在给定条件下分成DX1和DX2两部分，数据条数分别为x1和x2，则基尼分割系数可以表述如下[5]：

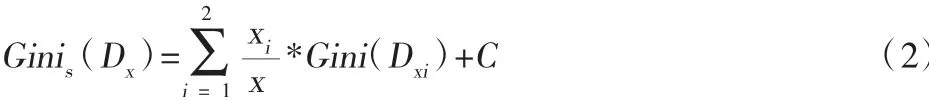
其中C为本文定义的扰动常量。一般地，我们可以写出其通项表达式：

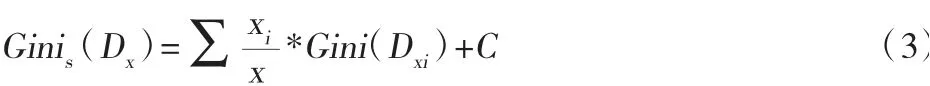
2.递归。在CART决策树算法的递归过程中需要将输入设置为训练集、基尼分割系数的阈值和切分的最少样本个数阈值；将输出设置为分类树。本文所进行的两个板块分析，算法分别从根节点“您在文科类科研、学习过程中对数学知识、模型需求量大吗”、“如果有这样一个能够将数学知识、方法、模型按照文科类科研、学习需求板块化分类的网站，您认为这样的网站能多大程度提高您的科研、学习效率？”开始，用训练集递归建立CART分类树。

3.剪枝。在运用CART决策树算法构建决策树的过程中，容易出现由于节点划分太细而产生过拟合的情况。当遇到此种情况时，可通过剪枝解决。本文在构建决策树过程中主要采用了“后剪枝”的方法进行修剪使得“文科类科研人员对数学知识模型需求”与“从网站中获益提高科研学习效率”相关参量能够得到有效利用的同时又不至于信息冗杂。

（二）CART决策树算法特点

决策树(decision tree)算法是一种基于树结构来进行决策的算法，典型决策树算法有ID3、C4．5和CART算法，本文所使用的CART算法采用基尼系数替代熵模型作为划分子树的依据，使得整体运算量较低，极大地提高了运算效率。同时该算法将多叉树改为二叉树（如本文所构建第一个二叉树的分类变量为“您所在的主修专业或科研方向”），因此，其对于子树拆分的次数没有限制。另外，值得提出的一点是，在CART算法之中所提取的特征可以重复使用，这一点使得该算法对于信息的利用率更高。CART决策树算法包含分类决策树和回归决策树，本文主要应用其中的分类决策树进行文科类科研人员对数学知识模型的需求分析，并进一步对他们从“提供数学知识模型帮助的网站中获益程度的期望”进行探究。

三、基于决策树算法的分析

（一）不同类型文科类科研人员对数学知识模型的需求情况决策树结果及解读

基于对“文科类科研人员的数学知识模型需求”这一主题进行探究的目的，我们展开了抽样调查。本次抽样调查采用多阶段抽样方法、PPS抽样、分层随机抽样和系统抽样相结合的概率抽样调查方式，对不同层次城市的文科类科研人员进行抽样调查，调查为期16天，采用线上线下调研相结合的模式共发放问卷1164份，其中806份来自线下调研，其中358份来自网络调查。通过对无效问卷的剔除，最终回收有效问卷1001份，总有效回收率为86.0%，问卷回收的具体情况如表1所示。

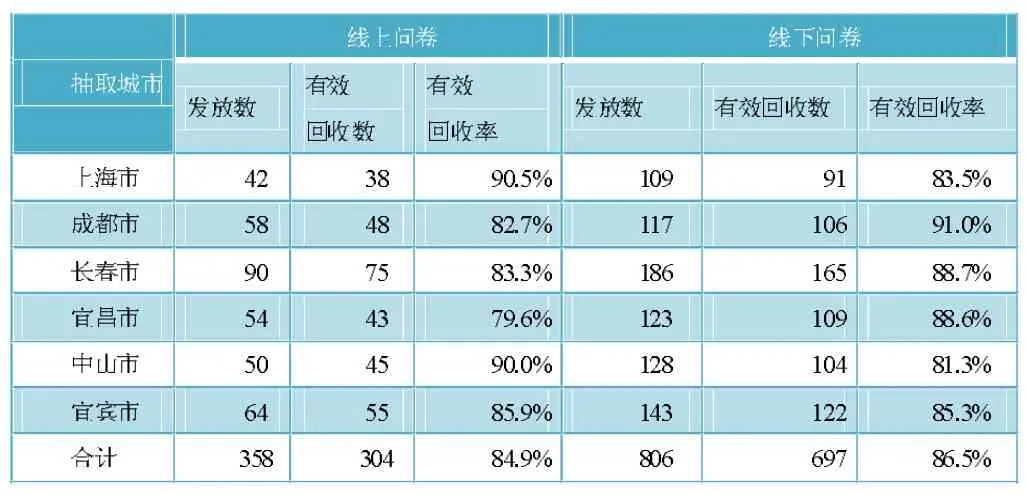
表1 问卷回收统计表

我们以有效问卷中的“文科类科研人员在文科类科研、学习过程中对数学相关知识、模型需求情况”内容为核心进行探究，可以直观观察到仅有13%的文科科研人员对数学知识模型的需求量较小或几乎不需要；而13%的受调查者表示对数学模型的需求一般；74%的受调查者对数学模型的需求量较大或很大。这表明大部分文科科研工作者在学习科研中存在对数学知识模型的依赖，但他们自身又缺乏相关的知识结构和获取途径。因此，对数学知识、模型进行系统整理和分类，将简化后实用易懂的数学知识模型提供给文科类科研人员这一尝试很有必要，且能够很大程度地提高文科类科研人员的工作效率。

我们对抽样所得到的数据进行预处理剔除无效数据后，基于不同类型文科类科研人员的情况构建了CART决策树探究了其对数学知识模型的需求。针对这一问题的决策树共有四层，根节点共包含866个样本，其中倾向类别1（几乎不需要数学知识模型）的有110人，倾向类别2（需求量一般）的有317人，而倾向类别3～5（有较大或很大需求量的）有439人，分别占比12.7%、36.6%、50.7%，这一数据表明有很大一部分文科类科研人员在进行学术科研和工作的过程中都需要数学知识模型的辅助，因此，对数学知识模型进行整理、分类和简化处理这一尝试具有很大的发展前景。在选择的变量里，决策树的第一最佳分组变量为“您所在的主修专业或科研方向”，并以此形成二叉树，最终得出结论和建议如下：

选择主修专业或科研方向为文学、管理类、教育学、法学、哲学（编号为6.0、8.0、3.0、5.0、1.0）的占比97.0%，作为重点探究对象，下一级分组变量是从事学术科研所在的城市，选择三线城市和其他（编号分别为4.0、5.0）的占总比重的70.2%，这可能是由于三线城市和其他层次城市科研压力相对较小所导致的。而选择二线城市、新一线城市、一线城市的占总比重的26.8%，这部分文科类科研人员在下一级分组变量——“您认为数学量化的方法已经是人文科研中普遍需要的方法了吗”的选择中差异化较明显（选择“不是”或“不清楚”的占总比重的20%，选择“是”的占总比重的6.8%），而在选择“是”的科研人员当中选择“对数学知识模型需求量较大”的占比最高，可以看出这类人群在学术科研中所需要数学知识模型支撑较多，且对数学量化的方法在文科科研的广泛应用持肯定态度。而选择“不是”或“不清楚”的文科类科研人员多从事教育学或文学相关工作，且选择对数学知识、模型需求量较少的占大多数。对于这类人群我们可以对他们进行数学知识模型成功辅助文科类科研案例的宣传，并针对他们的理解能力提供相应的数学知识、模型支撑。

重新聚焦第二级分组变量，选择三线城市和其他层次城市的文科类科研人员在“所在的专业或科研方向”上选择差异较大，其中从事文学或管理类学术科研的人员占总比例的56.9%，值得重点关注。这部分文科类科研人员在下一级分组变量——“您认为数学量化的方法已经是人文科研中普遍需要的方法了吗”的选择中差异较明显（选择不清楚”的占总比重的24.7%），这类科研人员对数学量化方法的应用广泛程度不太清晰，可能是由于他们在平时的学习科研中对数学量化方法的应用信息接触较少所导致的。当然，从决策树数据不难看出这类人群对数学知识模型的需求也相对较低。而从事哲学、教育学、法学的科研人员对数学量化的方法在文科类科研的广泛应用持肯定态度，且其中从事哲学、法学的科研人员选择对数学知识模型需求量为较高及以上的达到55.9%，对于这类人群我们应当在未来多提供相关数学知识模型的帮助，也可以为他们建立满足个性化需求的数学知识模型简化版辅助网站。

根据对决策树数据中根节点和叶子节点信息的综合分析，我们不难发现文科类科研人员对于数学知识模型是有一定需求量的，且他们也希望能够有一些辅助类网站或者其它辅助方案为他们提供满足个性化需求的数学知识模型。综上所述，未来的文科类学术科研将进一步融合数学理论方法，进一步提升其工作的创新性。

（二）文科类科研人员对提供数学知识模型帮助网站的受益程度期望认知情况

我们以有效问卷中的“文科类科研人员对提供数学知识模型帮助的网站的受益认知期望情况”内容为核心进行探究，发现仅有8%的文科类科研人员认为从提供数学知识、模型的网站中获益较小，而有超过60%的受调查者认为从此类网站受益较大或对此种辅助类网站对其非常有帮助。可见针对他们的个性化需求搭建和完善提供数学知识、模型的辅助类网站是一个有较广阔前景的研究方向。

在此分析基础上，本文进一步构建了CART决策树探究了文科类科研人员对提供数学知识模型帮助的网站的获益程度期望，此决策树一共有四层，根节点共包含784个样本，其中倾向类别1（受益程度较小）的有67人，倾向类别2（受益程度一般）的有242人，而倾向类别3和4（受益程度较大及以上）有475人，分别占比10.3%、30.2%、59.5%，表明有很大一部分文科类科研人员对提供数学知识模型帮助网站的受益程度较高，也说明对数学知识模型进行分类和简化处理后并发布到网站上这一尝试受到很大认可。在选择的变量里，决策树的第一最佳分组变量为“您认为数学量化的方法已经是人文科研中普遍需要的方法了吗”，并以此形成二叉树，最终得出结论和建议如下：

对第一级分组变量所对应的问题持“不清楚”态度的占比37.9%，在这类人群中以在“新一线城市”“二线城市”“三线城市”中从事学术科研的居多，占总比例的28.8%。而对于第一级分组变量所对应问题持清晰态度“是”或“不是”的占比62.1%，其所对应的第二级分组变量“您所在的主修专业或科研方向”选择差异性较大，其中选择“经济学”“管理学”的具有较高的一致性，占总比例的12.2%，对于这类人群，其对应的下一级分类变量为“您从事文科类学术科研所在的城市”，在这一级分类下，在“三线城市”从事学术科研的科研人员较多，且这类人群对提供数学知识模型帮助网站的受益程度期望较高及以上达到50%，由此可见，我们可以针对该类主要位于三线城市人群进行“经济学”“管理学”所涉及的数学知识模型运用引导，尽可能给他们提供一些去一线城市交流学习的机会，并针对他们的个性化需求不断完善现有辅助网站或努力打造更加智能化的辅助网站。

进一步分析发现，选择“哲学”“教育学”“法学”“文学”的科研人员具有较高的一致性，占总比例的49.9%，对于这类人群，在“一线城市”“二线城市”“三线城市”从事学术科研的人群后续信息具有较高的一致性，占总比例的27.8%，选择“新一线城市”“其他层次城市”的人群后续信息具有较高的一致性，且这一分类下对应的下一级分类变量“您所在的主修专业或科研方向”特征上具有差异性，其中选择“教育学”和“文学”的人员比例较高，这类人群中对提供数学知识模型帮助网站的受益程度期望较高及以上达到57.2%。由此可见，对于该类人群我们可以进行其所涉及的数学知识模型运用引导，同时基于在不同城市从事学术科研人群的需求进行数学知识模型的普及和辅助网站的更新。

大多数的文科类科研人员认可数学知识模型对于其所从事的科研发展具有重要意义，但他们自身对数学知识模型的需求存在差异，主要是由工作地为不同层次城市以及从事的文科科研方向不同所导致的差异。因此，根据不同类型科研人员的差异化需求整理出针对他们需求的简化版本数学知识模型并在辅助类网站中进行展示是很有意义的一项工作。

（三）结论

首先，在学科融合、学科交叉的时代背景下，数学与文科实现进一步的交流融合是历史发展的潮流，对于文科进一步的研究提供数学模型是推动两者交融发展的重要一步。其次，文科科研需要注入新活力，在数字信息时代，大多数的文科科研人员以及相关学生对于数学知识具有需求。最后，面对社会文科发展的差异性，区别具体化信息服务尤为重要，搭建平台提供数学模型，满足各个层面各个阶段文科研究具有现实意义。

四、结语

基于学科交叉应用逐渐加强，文科类科研人员存在对数学知识、模型需求的现状，本文通过CART决策树算法分析了不同类型、不同需求文科类科研人员对数学量化方法影响度及数学知识模型的需求，并结合调研数据进行了文科类科研人员对提供整理封装好的数学知识模型的辅助类网站的获益程度分析，综合上述结果为未来数学知识模型如何更好地为文科类科研人员提供帮助提出了建议。