基于交互信息的两阶段特征选择算法
刘 强,降爱莲
(太原理工大学 信息与计算机学院,山西 晋中 030600)
0 引 言
传统基于相关-冗余性分析的特征选择算法[1,2]表现出良好性能[3,4],这类算法可以有效选取强相关特征、去除无关特征和冗余特征,但是会遗漏部分与类标签相关度不高,与其它特征组合后有较强相关性的特征。为提高特征选择的精度,一些算法同时利用特征相关性、冗余性及互补性。如文献[5]在搜索过程中考虑互补性,基于自适应损失函数惩罚冗余并奖励互补,对于小样本数据,它在三者之间提供最佳的权衡,但会受到所选搜索策略的影响。文献[6]采用两阶段方式提高特征子集的选择效率,去除不相关特征和冗余特征的同时,选择与已选特征集合互补性最大的特征,但忽略了候选互补特征与已选特征集合间的冗余性。
基于上述情况,本文提出一种基于交互信息的两阶段特征选择算法。该方法能有效消除不相关特征并保留强相关特征,其次兼顾候选冗余特征与已选特征之间的互补性和冗余性,准确选取与已选特征发挥正向协同作用的“冗余”特征。实验结果表明,该方法能准确选择重要特征,有效提升数据分类准确率。
1 相关工作
最早使用互信息的方法是互信息最大化(mutual information maximization,MIM)[7],是一种直接的特征选择策略,利用互信息度量特征与类标签之间的相关度,选取重要特征。尽管MIM具有较低的时间复杂度,但它忽略了特征之间的冗余性。为了减少冗余信息,Battiti等[8]提出基于互信息的特征选择算法(mutual information based feature selection,MIFS),该方法通过度量候选特征与类别标签之间的相关性,以及候选特征与已选特征集合的冗余度,对候选特征打分,选取重要特征。但随着数据维数的增大,MIFS的冗余项相较于相关项会变的很大,这意味着该方法可能选择不相关的特征。最大相关-最小冗余算法(maximum relevance minimal redundancy,mRMR)[4],则利用候选特征与已选特征之间的平均冗余度,表示损失函数的冗余项,防止冗余项过大。但是,关于互信息有一个潜在的问题,它倾向于取值较多的特征。为了避免这种情况,一些研究通过将互信息的值缩放到 [0,1], 对互信息进行归一化处理,例如归一化互信息特征选择算法(normalized mutual information feature selection,NMIFS)[9]。上述方法都较为有效地考虑了特征的相关性和冗余性,但都存在一定局限性:①需预设特征个数;②利用贪心搜索策略,计算代价高;③忽略了特征间的交互作用。
针对前两个问题,基于相关性的快速过滤器(fast correlation-based filter,FCBF)[10]提出近似马尔可夫毯理论,从而达到快速消除冗余的目的。FCBF无需预设所选特征个数,并且利用对称不确定性,克服使用互信息带来的偏置。但该方法在某些情况下存在将强相关特征误判为冗余特征的问题,意味着该方法可能会漏选重要特征。为了准确选择强相关特征,基于特征分组的过滤器(filter-based feature selection by feature grouping,FFSG)[11]在近似马尔可夫毯理论的基础上提出了强近似马尔可夫毯理论。对于交互问题,为了识别交互特征,一些方法引入其它标准来选择特征。例如,联合互信息最大化方法(joint mutual information maximization,JMIM)[12],通过联合互信息考虑已选特征与候选特征的交互作用,并利用“最大最小”准则来选择最相关的特征。基于交互权重的特征选择算法(interaction-weight-based feature selection,IWFS)[13],则利用交互信息评估候选特征。该方法通过交互权重因子来反映候选特征是交互还是冗余的。
一般情况下,大多数方法都是通过最大化交互信息来考虑互补性,通过评价函数的方式对特征打分,根据分值选取前K个特征。但这些方法需要预设所选特征个数。因此,有必要制定更简便的方法。
2 相关概念
定义1 互信息[14]。互信息可以用来衡量一个随机变量中包含另一个随机变量的信息量。给定两个离散型随机变量X={x1,x2…xn} 和Y={y1,y2…ym},X和Y之间的互信息定义为
(1)
其中,p(xi) 表示值xi在X中发生的概率,p(xi,yj) 为xi和yj分别在X和Y中同时发生的概率。
定义2 对称不确定性[10]。对称不确定性是归一化的互信息,其值限制在 [0,1]。X和Y之间的对称不确定性定义为
(2)
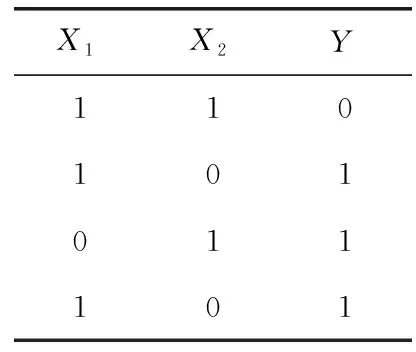
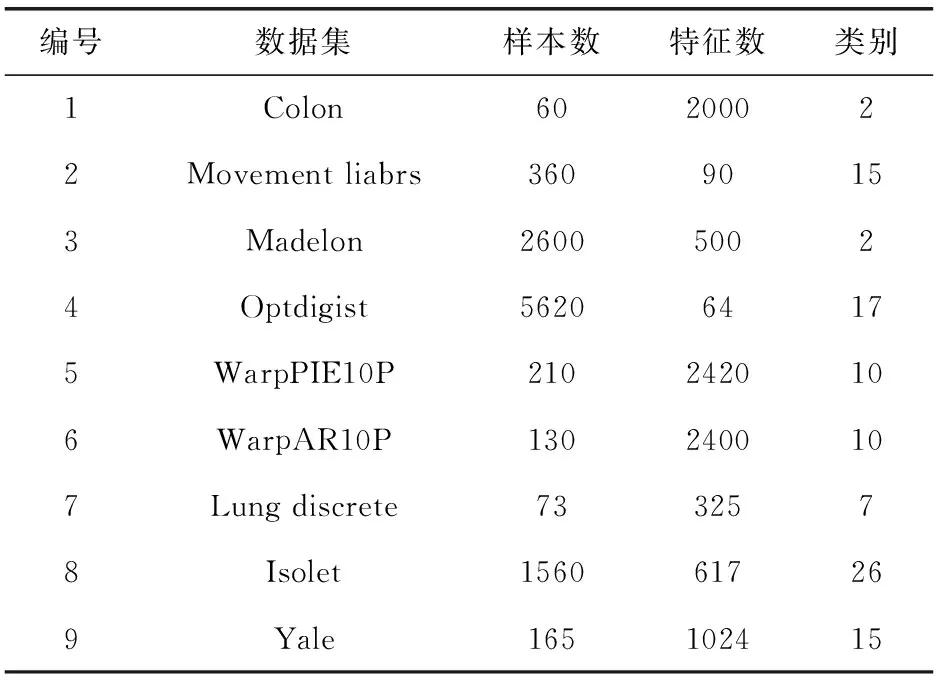
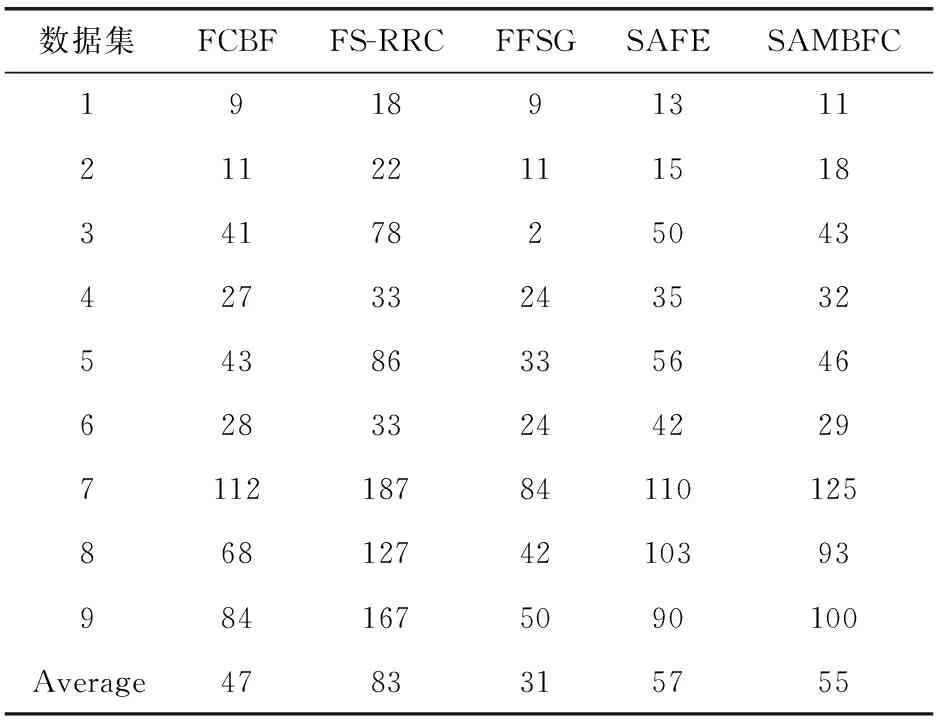
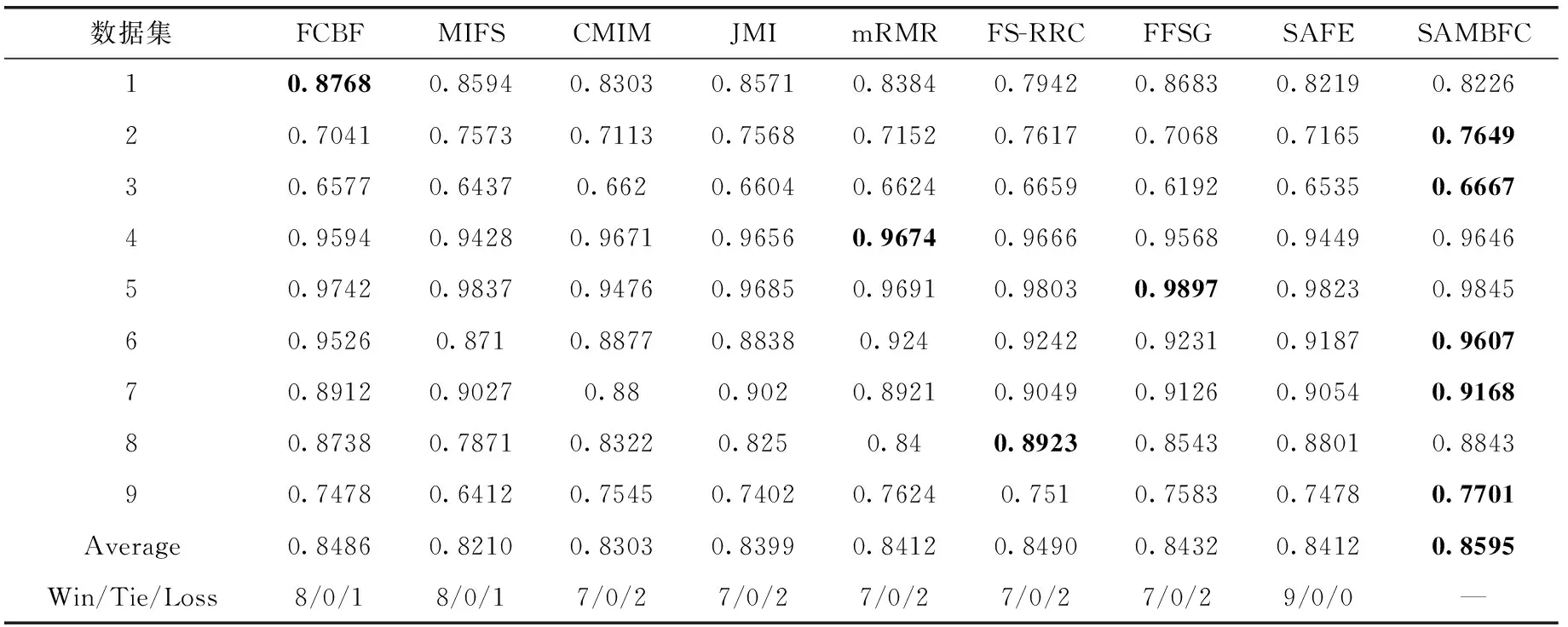
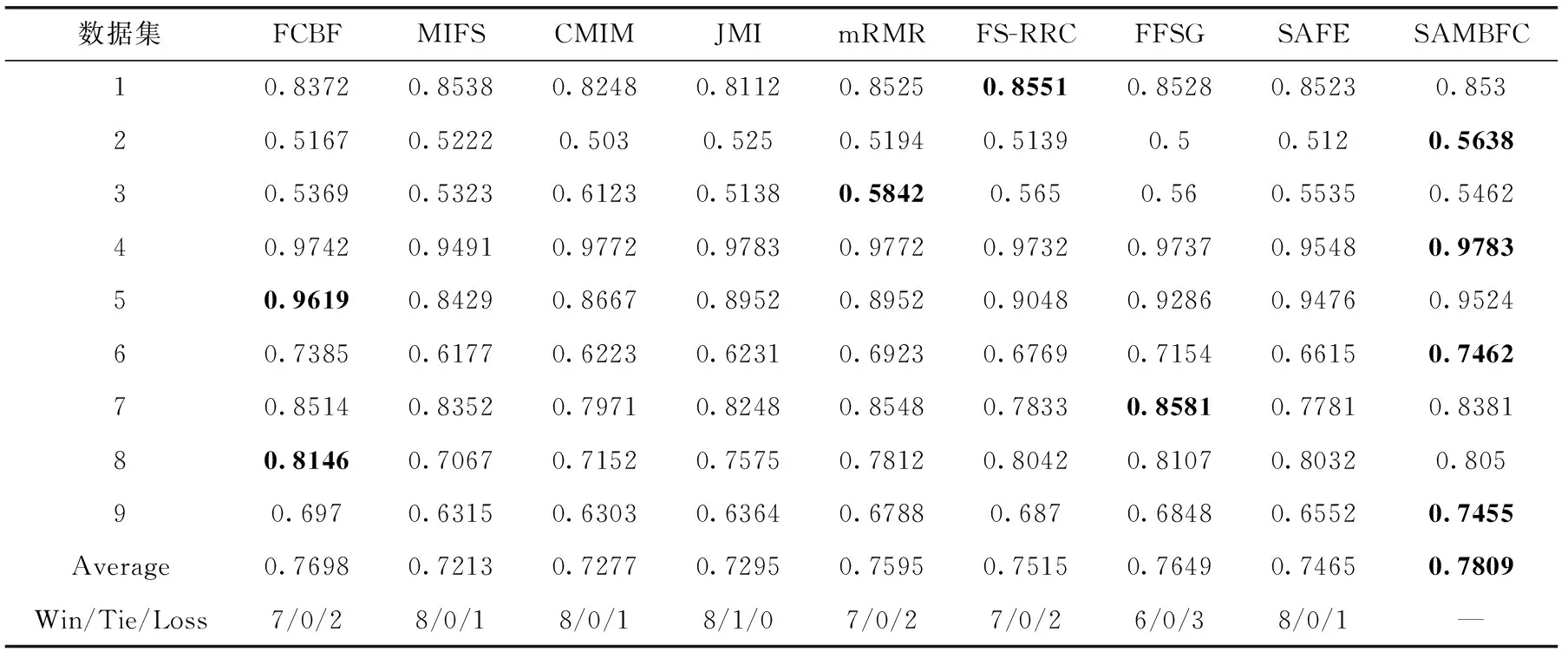
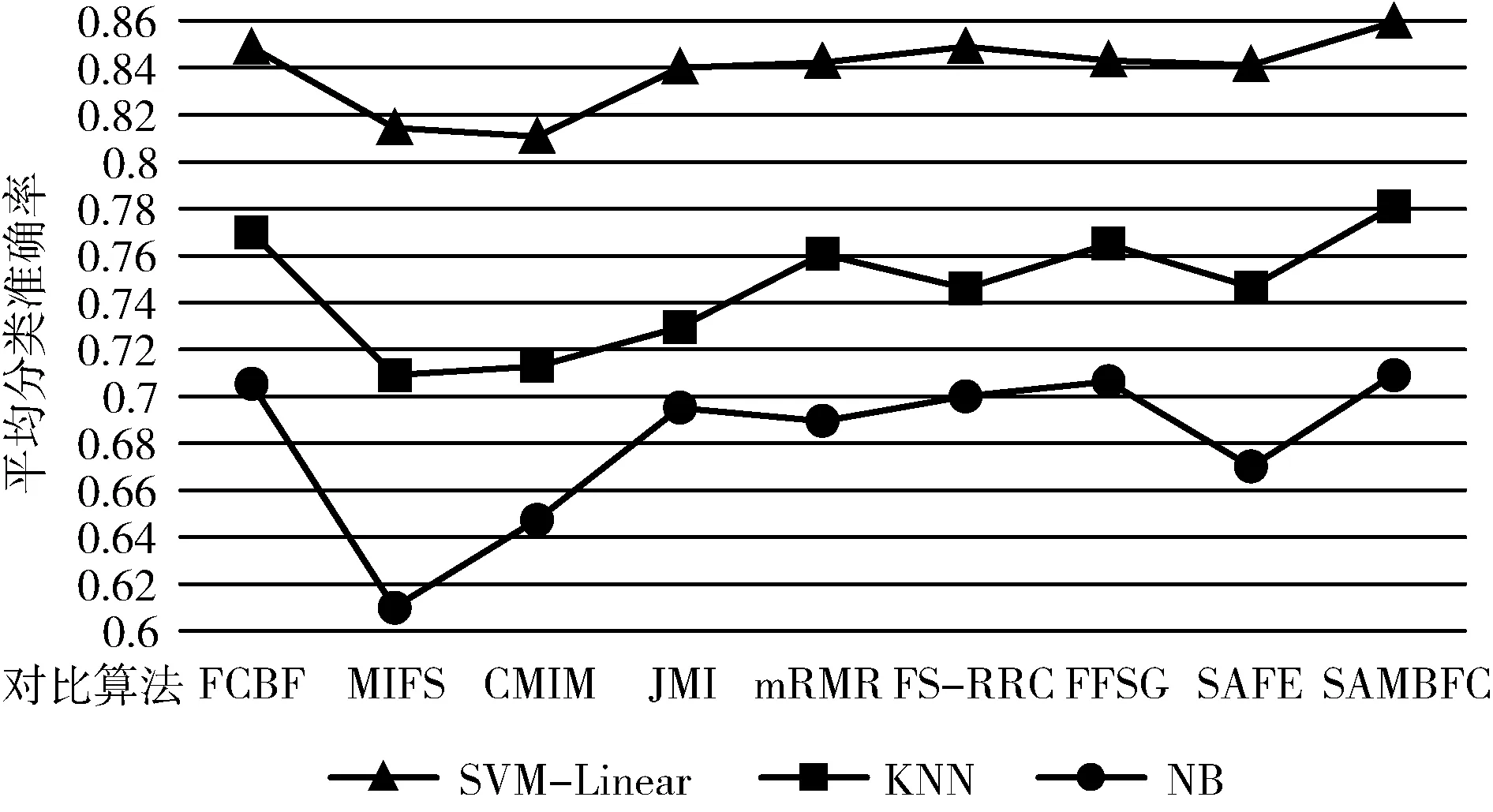
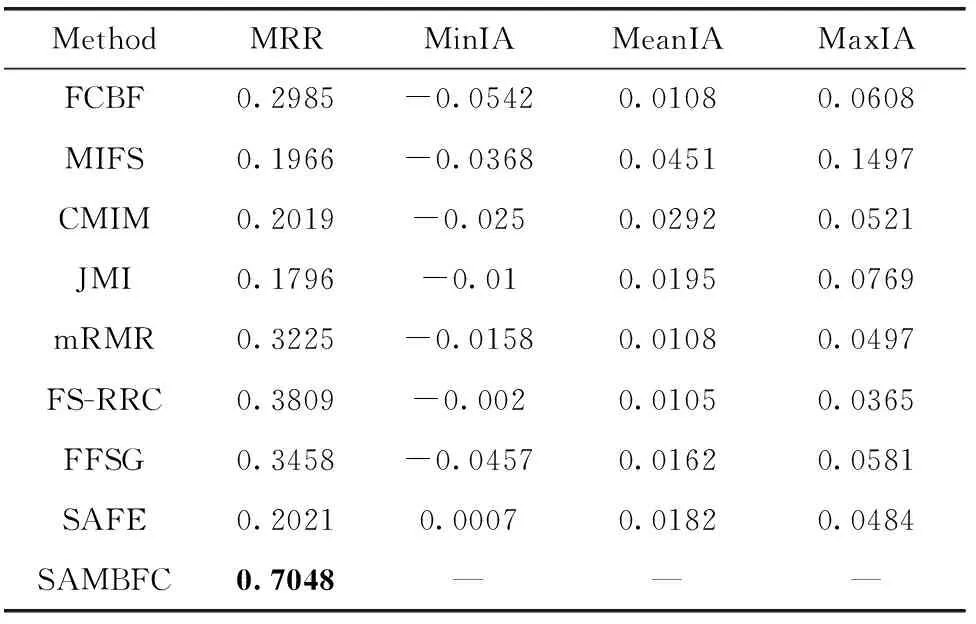
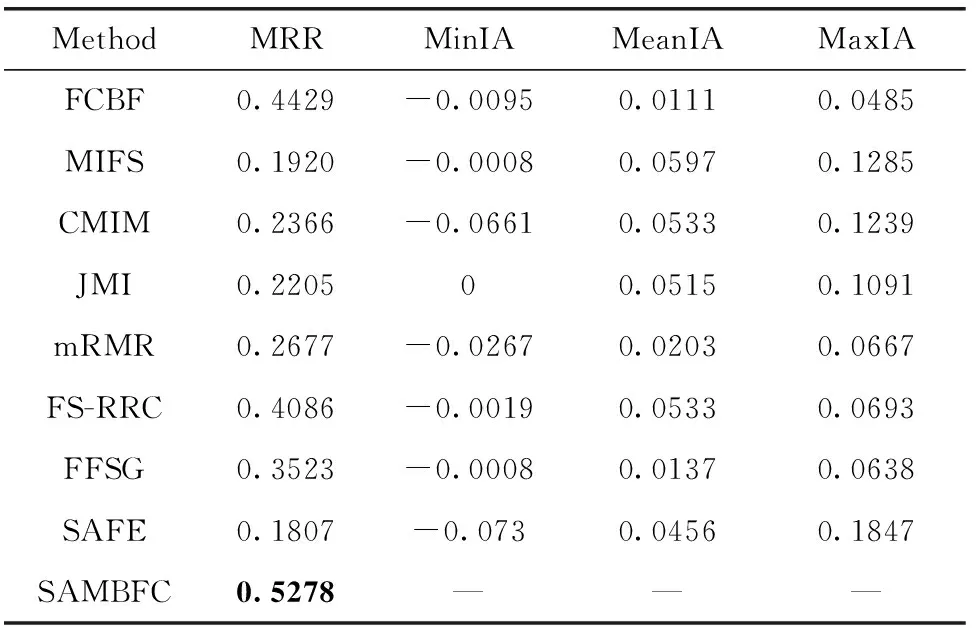
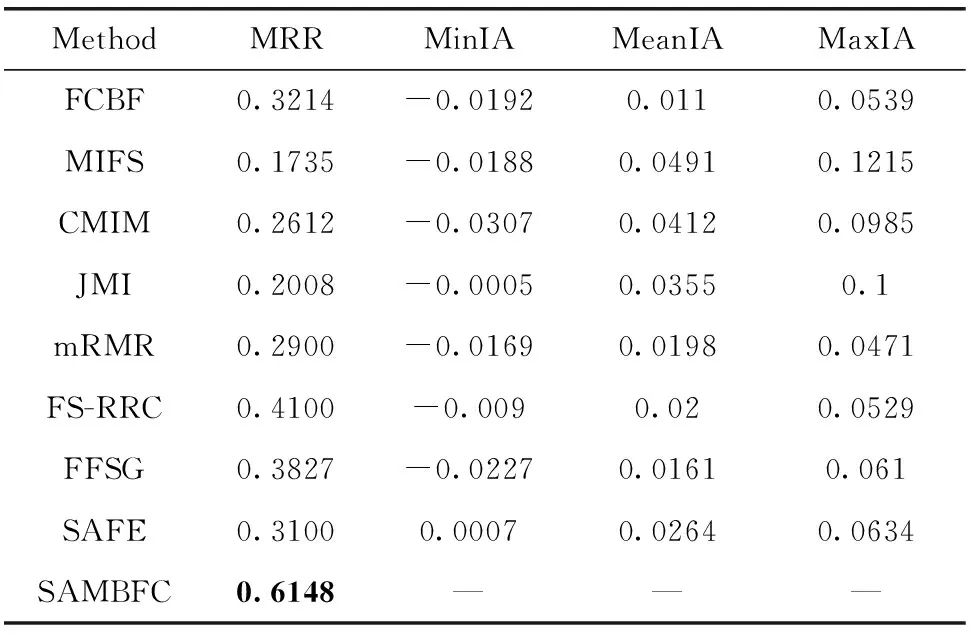
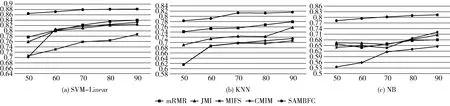
其中,H(X) 为X的信息熵,表示X中包含的信息量。SU(X,Y)=0时,表示两个变量之间相互独立。 0 定义3 马尔可夫毯[15]。给定一个特征Xi∈F, 其中类标签为Y,若特征子集Mi⊂F(Xi∉Mi) 为Xi的马尔可夫毯,当且仅当Xi⊥{F-Mi-{Xi},Y}|Mi。 其中⊥表示独立, |Mi表示在给定Mi的条件下。即在给定Mi的条件下,Xi独立于特征集合F-Mi-{Xi} 和类标签Y。 说明Mi中包含了Xi对类标签Y和其它特征集合F-Mi-{Xi} 的所有相关信息,则Xi相对于Mi为冗余特征。 定义4 强近似马尔可夫毯[11]。给定两个相关特征Xi,Xj≠i∈F, 若Xi构成Xj的一个强近似马尔可夫毯,当且仅当满足 (3) 定义5 交互信息[16]。给定两个特征Xi和Xj,Xi和Xj之间的交互信息定义为 I(Xi;Xj;Y)=I({Xi,Xj};Y)-I(Xi;Y)-I(Xj;Y)= (4) I(Xi;Xj;Y)>0, 表示Xi和Xj组合后发挥正向协同作用,提供Xi或者Xj单独存在时不能够提供的信息;I(Xi;Xj;Y)=0, 表示Xi和Xj包含相同的信息;I(Xi;Xj;Y)<0时,表示Xi和Xj组合后会带来更多冗余信息。 定义6 冗余特征。Xj为特征集合F中任意一个特征。若Xj为冗余特征,当且仅当存在Xi≠j∈F构成Xj的一个强近似马尔可夫毯。 定义7 强相关特征。Xi为特征集合F中任意一个特征。若Xi为强相关特征,当且仅当F中没有任何特征是该特征的强近似马尔可夫毯。 定义8 基于相关性特征选择算法[17]。基于相关性算法(correlation based feature selection,CFS)通过评估特征间以及特征与类别标签之间的相关性来评估特征子集。该算法保留与类标签高度相关,但与其它特征无关的特征,可以有效去除对类预测不起作用的特征变量,评价函数为 (5) 为防止漏选重要特征,而导致有用信息的丢失。本文提出基于交互信息的两阶段特征选择算法,主要分为以下两个阶段:①相关-冗余性分析。首先去除无关特征,然后利用强近似马尔可夫毯原理选取强相关特征,得到一个高相关、低冗余的次特优子集。②互补-冗余性分析。首先分析冗余特征,从中选取主互补特征,然后利用CFS算法分析该特征的优劣,确定是否将该特征加入已选特征集合中。最终得到一个兼顾特征相关性和互补性的最优特征子集。 为准确去除无关特征,并保留强相关特征,本文利用对称不确定性和强近似马尔可夫毯理论分别对特征进行相关性和冗余性分析,具体过程如下: (1)相关性分析。对于特征集合F={X1,X2…Xn}, 根据式(2)计算F中所有特征与类标签的相关度,并从F中去除所有与类标签相关度为0的无关特征,保留与类标签具有一定相关度的特征。 (2)特征排序。计算F中每一个特征与其它特征间的冗余度,如式(6)所示,并按照特征间冗余度对F中特征降序排序 (6) 由所有强相关特征组成的特征子集为次特优子集,该集合中特征与类标签相关度高,并且特征间冗余度低。基于强近似马尔可夫毯原理,可以有效防止强相关特征被误判为冗余特征;而且所有被删除的特征都能从该集合中找到相应的强近似马尔可夫毯。 现有的大多数特征选择算法都通过最大化特征与类标签之间的相关性、最小化特征间冗余来选择重要特征。但特征间关系较为复杂,部分特征之间可能存在交互作用。即单个特征与类标签的相关性较小,但与其它特征组合后却与类标签有较强相关性。表1中的示例说明了这一现象。 表1 互补性示例 表1中特征X1和X2都不能提供较多的分类信息:I(X1;Y)=0.085、I(X2;Y)=0.216。 若不考虑特征间的交互作用,X1和X2有可能被误判为冗余特征。但X1和X2组合后I({X1,X2};Y)=0.477>I(X1;Y)+I(X2;Y), 却可以提供更多分类信息,说明X1和X2不是真正的冗余特征。因此,在选出强相关特征的基础上,冗余特征的分析决定了最终所选特征子集的优劣。为准确、简便地分析特征间的交互信息,本文提出一种分析候选冗余特征与已选特征间交互作用的方法。该方法将互补-冗余性分析相分离,分别对冗余特征进行互补性分析和冗余性分析。具体方法为: C(Xi,Xj,Y)=SU(Xi,Y|Xj)-(1+λ)SU(Xi,Y) (7) (8) (3)冗余性分析。对于主互补特征Xc, 与Xi组合后发挥正向协同作用,但与Xlist中其它已选特征组合后可能发挥负向协同作用,因此有必要分析加入Xc后给整个已选特征集合带来的影响。首先,根据式(5)计算Xlist的整体价值;然后将Xc加入Xlist中,并计算此时Xlist的整体价值。若加入Xc后Xlist的整体价值有所提升,则保留该特征,否则不加入该特征。 (4)以此类推,直至分析完Xlist中所有已选特征的主互补特征,得到最优特征子集Xbest。 根据SAMBFC的两阶段选取过程,给出下面相应的两部分算法。其中,阶段1为选取强相关特征,阶段2为分析冗余特征。 第一阶段:选取强相关特征 输入:数据集D,特征集合F={X1,X2…Xn} 其中Xi={x1,x2…xm}, 标签集合为Y={y1,y2…ym} (1)Xlist←∅SC←∅Xbest←∅F*←∅ (2)for eachXi∈Fdo (3) ifSU(Xi;Y)=0 (4)F←F (5)end for (6)for eachXi∈Fdo (8)end for (9)F←sort(F) whereRi>Rj (10)for eachXi∈Fdo (11)Xlist←Xlist∪{Xi} (12) for eachXj≠i∈Fdo (13) IfSU(Xi,Xj)>δandSU(Xi,Xj)≥SU(Xj,Y) andSU(Xi,Y)≥SU(Xj,Y) (15) end for (16)end for 阶段1中主要是利用强近似马尔可夫毯原理,将原始特征空间,划分为强相关、无关以及冗余子集,其中(2)~(5)行筛选无关特征,第(11)行选取强相关特征,(13)、(14)行识别冗余特征。 第二阶段:分析冗余特征 输出:最优特征子集Xbest (1)SC←∅Xbest←∅Xc←∅ (2)for eachXi∈Xlistdo:Xj∉SC (4) ifC(Xi,Xj,Y)>0 (5)XC←Xj∪{XC} (6) end for (8)SC←SC∪{XC} (9)end for (10)for eachXc∈SCdo (11)Xbest←Xlist∪{Xc} (12) ifJ(Xbest)>J(Xlist) (13)Xlist=Xbest,J(Xlist)=J(Xbest) (14)end for 阶段2主要是分析冗余特征,选择出能增强已选特征集合与类标签相关性的互补冗余特征,其中(2)~(9)行选出主互补特征,(12)、(13)行分析该特征的优劣。 第一阶段中计算特征与类标签间相关性的时间复杂度为O(n), 计算特征间冗余度的时间复杂度为O(mn2), 特征排序的时间复杂度为O(nlogn), 删除冗余特征的时间复杂度为O(n2), 因此第一阶段的时间复杂度为O((m+1)n2+nlogn+n)=O(mn2)。 由于在第一阶段已经去除大量无关和冗余特征,会减小第二阶段的特征计算规模,所以第二阶段所需时间复杂度远小于第一阶段。因此,SAMBFC算法的总时间复杂度为O(mn2)。 本文在UCI和ASU上的多个公开数据集进行对比实验,数据集涉及医学、生物信息学、图像等领域,具体参数见表2。实验前利用类别属性依赖最大化方法[18](class-attribute interdependence maximization,CAIM)将连续型数据离散化。 表2 实验所用数据集 为了验证本文所提SAMBFC算法的有效性,实验过程中将与以下3类算法进行对比: (1)MIFS[8]、mRMR[4]以及条件互信息最大化(conditional mutual information maximization criterion,CMIM)[13],这3种算法是传统的基于相关-冗余性分析的。 (2)FCBF[10]和FFSG[11]分别基于近似马尔可夫毯理论和强近似马尔可夫毯理论进行相关-冗余性分析。 (3)自适应特征评估(self-adaptive feature evaluation,SAFE)[5]算法、基于特征相关性、冗余性和互补性(feature selection based on relevance、redundancy and complementarity,FS-RRC)[6]算法以及基于联合互信息(joint mutual information,JMI)[12]算法在特征选择的过程中考虑特征互补性。 实验中分别使用支持向量机(support vector machines,SVM)、朴素贝叶斯(Naive Bayesian, NB)和k-最近邻(K-nearest neighbor,KNN)分类器评估SAMBFC算法的性能。其中SVM来自LIBSVM工具包,内核选择线性核函数,该工具包中利用网格搜索确定惩罚因子等具体参数。KNN中的K值设为10,MIFS的β设置为0.5,FCBF的δ设置为0,SAMBFC的λ设置为0.1。实验采用5折交叉验证的方式,为保证公平,每个数据集都进行50次实验,通过计算50次结果的平均值来求得算法的分类表现。 由于SAMBFC算法无需预设选择的特征个数。为保证对比实验的有效性。所以,实验将分两部分算法进行对比。一部分为FCBF、FS-RRC、FFSG以及SAFE,4种无需预设特征个数的算法,另一部分为MIFS、mRMR、JMI、CMIM,4种需预设特征个数的算法。 4.4.1 分类性能 本节实验主要与4种无需预设特征个数的算法进行对比。此处将MIFS、mRMR、JMI、CMIM,4种特征选择算法选择的特征个数设置为SAMBFC选择的特征个数。表3给出了FCBF、FS-RRC、FFSG、SAFE和SAMBFC算法在9组数据集上选择的特征个数。 表3 5种算法选择特征个数 图1是9种算法在3种分类器上的分类表现。表4和表5分别是9种算法在SVM和KNN分类器上的具体分类准确率。Win/Tie/Loss,其中Win表示SAMBFC表现优于当前算法,Tie表示与SAMBFC算法表现一致,Loss表示当前方法优于SAMBFC算法。 表4 SVM-Linear分类器的分类准确率 表5 KNN分类器的分类准确率 图1 9个算法在不同分类器上的分类效果 (1)FFSG与SAMBFC算法对比 SAMBFC相较于FFSG,在SVM-linear上提升1.63%,KNN上提升1.6%。在SVM-Linear分类器上,FFSG方法除了在Colon、WarpPIE10P数据集上的表现优于SAMBFC方法,其余数据集上表现较差,在KNN分类器上,在Colon、Madelon和Lung discrete数据集上表现优于SAMBFC方法。SAMBFC相较于FFSG方法平均多选择了24个特征,多出的特征一部分是具有互补信息的特征,另一部分是FFSG筛选次特优子集后删除的特征,由于次特优子集中绝大部是相关性较强的特征,删除部分特征后导致分类效果下降。SAMBFC虽然选择更多的特征,但总体表现优于FFSG方法。 (2)FS-RRC与SAMBFC算法对比 在SVM-Linear分类器上,SAMBFC算法相较FS-RRC算法提升了1.05%,在KNN上高出2.94%。表4中SAMBFC仅在Optdigist和Isolet数据集上低于FS-RRC算法。表5中在Colon、Optdigist数据集上低于FS-RRC算法,但在其它7个数据集上均高于FS-RRC算法。SAMBFC较于FS-RRC平均少选28个特征,但在9个数据集上表现优于FS-RRC算法或与其相近。因此SAMBFC相较于FS-RRC对于互补信息的评价更为准确,并且充分考虑到候选特征和已选特征集合间的冗余性,获得更优的特征子集。 (3)FS-RRC、FCBF与SAMBFC算法对比 FS-RRC是在FCBF的基础上加入了特征互补性。在SVM-Linear分类器上,FS-RRC除了在Colon和Warp-AR10P数据集上差于FCBF,其它7个数据集上表现均优于FCBF,表明互补特征能够带来更多信息,但也可能带来更多冗余。选择的特征个数增多但降低了分类准确率,表明FS-RRC算法中通过特征互补性加入的部分特征带来的冗余信息超过了互补信息,从而造成分类准确率的下降。而SAMBFC算法所提的度量方法能够较为有效衡量特征间的互补信息,从而提升分类效果。 (4)SAFE和SAMBFC算法对比 在两个分类器上,SAMBFC表现均优于SAFE,而且相较于SAFE方法平均少选择两个特征。SAFE以启发式的方式,从整个特征集合的角度来衡量特征之间的关系,虽然从整体衡量特征空间的相关、冗余及互补性更为准确,但SAFE算法在高维数据上表现较差,而且该方法会受到搜索策略的影响。 (5)MIFS、CMIM、JMI、mRMR和SAMBFC算法对比 从表4~表5中可以看到将MIFS、CMIM、JMI、mRMR算法选择的特征个数设置为SAMBFC选择出的特征个数时,SAMBFC整体表现优于其它算法。但将这几种算法选择的特征个数直接预设为SAMBFC选择的特征个数不能很好地对比几种方法的差异。在实验的最后部分本文对这几种算法选择特征的能力进行了更详细的对比。 由实验结果可知,SAMBFC算法总体优于这4种算法。从相关、冗余性的角度而言,SAMBFC算法利用强近似马尔可夫毯选出与类别高度相关、更有区分能力的特征,并且防止了强相关特征的误判。从互补性的角度来看,SAMBFC利用对称不确定性度量特征间的互补性,利用CFS算法度量候选特征与已选特征集合间的冗余度,能够更为公平、准确选择互补特征,获得更好的分类效果。 4.4.2 单独分类性能的统计表现 为了更加直观地描述特征选择算法的优劣程度,表6、表7是对表4、表5数据的统计分析,其中MRR是平均倒数秩[19],用来衡量一个方法的综合排名。例如SAMBFC在SVM上的表现排名为:7,1,1,5,2,1,1,2,1。则SAMBFC的MRR为 (1/7+1+1+1/5+1/2+1+1+1/2+1)/9=0.7048。 MinIA、MeanIA和MaxIA是SAMBFC的分类准确率减去每个方法的分类准确率后的最小值、平均值和最大值。表5、表6中的数据表示,SAMBFC在两个分类器上的综合表现均为最优。 表6 9种方法在SVM-Linear上的统计表现 表7 9种方法在KNN上的统计表现 4.4.3 平均分类性能的统计表现 由于每种方法都有它各自的特点或优势,因此单个分类模型上的性能好坏,并不足以说明选择算法的性能优劣。为了能从整体上描述不同选择方法的性能,将在表4和表5中的分类表现求和后取平均值,对其统计表现进行分析,其具体数值见表8。表8中结果表明SAMBFC的平均分类表现在几个方法中也是最优。 表8 平均分类性能的统计表现 为了更好对比MIFS、CMIM、JMI、mRMR与SAMBFC算法之间的性能。通过约束SAMBFC方法选择的特征个数,将这几种方法选择的特征个数预设为50、60、70、80、90。由于SAMBFC算法在Lung discrete、Isolet以及Yale数据集上选择特征个数较多,所以此处在这3个数据集上进行对比实验。 图2~图4则是几个方法在选择不同特征个数时的表现。从图2中可以看出,在Isolet数据集上SAMBCF算法的分类效果明显优于其它MIFS、CMIM、JMI、mRMR算法。图3(c)中,SAMBFC算法在分析Lung discrete数据集时,在NB分类器上选择较少特征个数时表现与其它方法相近,随着所选特征个数的增多,分类表现逐渐优于其它算法。图4(b)中,SAMBFC除了在KNN分类器上,选择特征个数为50和60时表现不佳,其余情况下表现均优于其它方法。因此,SAMBFC算法选择特征能力总体优于其余4种特征选择算法。 图2 5种方法在Isolet数据集上的分类效果对比 图3 5种方法在Lung discrete数据集上的分类效果对比 图4 5种方法在Yale数据集上的分类效果对比 针对传统特征选择中,因忽略特征间协同作用而漏选部分重要特征的问题,本文提出了一种基于交互信息的两阶段特征选择算法。该方法对特征进行两阶段选取,在选取强相关特征后,对冗余特征进行互补-冗余性分析,选取具有交互作用的冗余特征。在9个公共数据集上将本文算法与FCBF等8种特征选择算法进行对比实验。实验结果表明,相较其它算法SAMBFC选择了更优的特征子集,提高了分类准确率,然而本文算法仅考虑了两两特征间的交互作用。未来将对候选特征与整个已选特征集合间互补性的度量进行研究。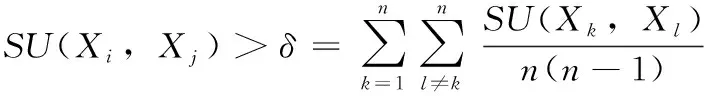
I(Xi;Y|Xj)-I(Xi;Y)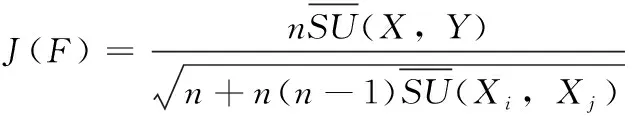
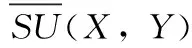
3 本文算法
3.1 相关-冗余性分析
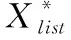
3.2 互补-冗余性分析
3.3 算法伪代码
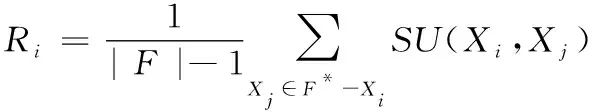
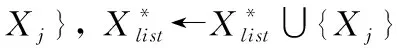
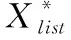

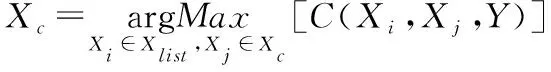
4 实验与结果分析
4.1 实验数据
4.2 实验对比算法
4.3 实验设置
4.4 结果分析


5 结束语

