海洋条件下安注水箱晃荡特性实验研究

魏天一，张 彪，谭思超,*，李东阳，李忠意

(1.哈尔滨工程大学 黑龙江省核动力装置性能与设备重点实验室，黑龙江 哈尔滨 150001；2.哈尔滨工程大学 核安全与先进核能技术工信部重点实验室，黑龙江 哈尔滨 150001；3.中广核研究院有限公司，广东 深圳 518000)

浮动核电站在风浪涌、地震及海啸等海洋环境中受到复杂的运动激励，安注水箱等储液设备在运动条件下会发生晃荡，晃荡导致的液面波动会干扰液位测量和压力控制，且引入的流体抨击载荷将影响结构强度和设备寿期，不利于浮动核电站的安全运行[1-2]。

自由液面容器的晃荡研究长期以来受到国内外学者青睐。在理论方面，解析晃动固有频率对实验研究和工程实践具有指导意义，基于模态分析已证明圆柱腔等规则容器内固有频率等晃动特征问题存在解析解[3]。在实验方面，能表征液位高度和流体抨击的压力信号是反映晃荡特性的核心参数，故压力测量的高频响应和空间布置是晃荡实验研究的关键。卫志军等[4-5]在不同运动振幅和频率下借助比例模型研究了水平晃动条件下压力载荷的分布，明确了实验测量在复杂晃荡研究中的必要性。吴文军等[6]和Pistani等[7]在实验中发现共振频率附近为水跃冲击多发区域，但其测量和分析对象多为液舱和燃料箱等非核设备。陈佳睿等[8-9]用激光诱导荧光法记录了横荡条件下液面瞬态晃动过程，并讨论了液面变化和压力波动的关系。研究结果表明，可视化分析可为晃荡研究提供直观依据。此外，浮动核电站设计中关于海上强耦合运动对安全运行的影响问题愈发受到重视，故在运动频率和耦合形式上对实验研究提出了更高要求[10-11]。

本文选择安注水箱为研究对象，依托哈尔滨工程大学六自由度运动平台开展海洋条件下晃荡特性实验，通过多方位布置高频传感器采集压力信号，使用高速相机记录液面瞬时晃动过程，同时基于固有频率计算和时频域分析，研究典型海洋条件下安注水箱的压力变化规律和晃荡演化特征。

1 实验系统

运动条件下多参数综合测量系统示意图如图1所示，本实验系统主要由安注水箱缩比模型、六自由度运动平台、光学测量系统、惯性导航设备、循环水箱、各类泵阀及管道等构成。安注水箱模型材质为有机玻璃，中间部分为规则圆柱腔，通过粘结和螺栓连接装配上下半球形封头；六自由度运动平台高约2 250 mm，承重能力高达2 t，可完成单自由度摇荡运动及多类复合运动；实验工质采用常温蒸馏水，其中添加适量水溶色素以辨别自由液面；安注水箱侧壁面多点开孔，与微型高频压力传感器连接，压力传感器量程为0～10 kPa，延迟为μs级别，且与流体接触面积小于28 mm2；船用BZD271惯性导航系统放置在平台边缘且处于摇摆轴位置，可实时输出三轴角度、角速度等姿态数据；高速相机和LED光源位于横摇中轴的远端并与平台连接固定，与其同步运动，以20 Hz频率记录瞬时晃动过程；操作人员通过上位机输入运动信号来模拟真实海洋条件。

图1 海洋条件下多参数综合测量系统Fig.1 Multi-parameter measurement system under ocean condition

压力传感器布置示意图如图2所示。该布置形式参考ACPR50S原型实际压差测量方案，在摇摆(或晃动)条件下，与运动轴线垂直(或重合)平面处的流体所受影响最大。为得到显著的运动激励反馈，将4块配置相同的压力传感器对称布置在安注水箱模型壁面，均位于运动中轴线附近，其中测点P1距离底部中心247.5 mm，以测点P1的位置高度为基准，测点P′1相对高度为55.5 mm， 测点P2相对高度为-30.3 mm，测点P′2相对高度为-81.2 mm。

图2 压力测量点位置Fig.2 Pressure measurement point position

2 工况设定与结果分析

本文所描述的海洋条件通常指海洋运动条件[12]，参照船舶与海洋工程学科中的运动形式分类以及《船舶环境条件要求 机械环境》(GJB 1060.1—1991)中标准定义，将复杂海洋条件拆解为图3所示的运动形式，包含横摇、纵摇、横荡、纵荡、艏摇和垂荡等6种基本单自由度运动。考虑实际运行中，艏摇为非典型运动条件，垂荡无显著液晃特征，故选择摇摆运动、水平晃动及其耦合运动作为代表性激励条件，结合实验研究依次阐述分析。

图3 海洋运动条件Fig.3 Motion form under ocean condition

2.1 摇摆运动

摇摆运动(横/纵摇)是海洋条件中典型的绕轴运动，摇摆一方面使得安注水箱的空间位置发生相对变化，另一方面引入周期性力场造成液面波动。中广核研究院有限公司在浮动堆设计中的摇摆测验发现，8级海况使得摇摆角度可达20°～22.5°，且最小运动周期约为12.11 s，该程度的摇摆条件整体诱发概率约为1.09%。结合实际海试数据, 同时为包络浮动反应堆在海洋环境中面临的极限场景，本文设置摇摆角度最大为22.5°，周期处于5～20 s。

50%载液率条件下的液体晃荡过程如图4所示。在该严峻工况下自由液面整体上呈现平面驻波形式，即液面整体水平且与重力方向垂直，但运动至最大摇摆角度时壁面边缘处流体会有水跃上升。在极端高频率或大角度摇摆运动下，惯性影响超过重力下的自稳能力，液面难以建立或保持平稳状态，流体在动势能转换下向一侧迅速积聚后或出现水跃和行进波等非均匀波动，此时的压力波动规律会相应出现明显反馈。

图4 22.5°-5 s摇摆运动下的典型相位图Fig.4 Typical phase diagram under 22.5°-5 s rolling motion

摇摆条件和测点位置是影响压力测量的关键因素。不同摇摆条件下测点P2的压力对比结果示于图5a，可见测点压力波动周期同摇摆周期一致且压力振幅受摇摆角度影响，整体压力波动规律和外部运动激励信号一致。不同测点位置对压力测量的影响示于图5b，可见压力波动规律具有时空特性，测点P1和P′1的波动周期为运动周期的1/2，且因其位于横摇中轴位置，受液面晃动的影响相对轻微，所以压力波动幅值仅为测点P2和P′2的10%。

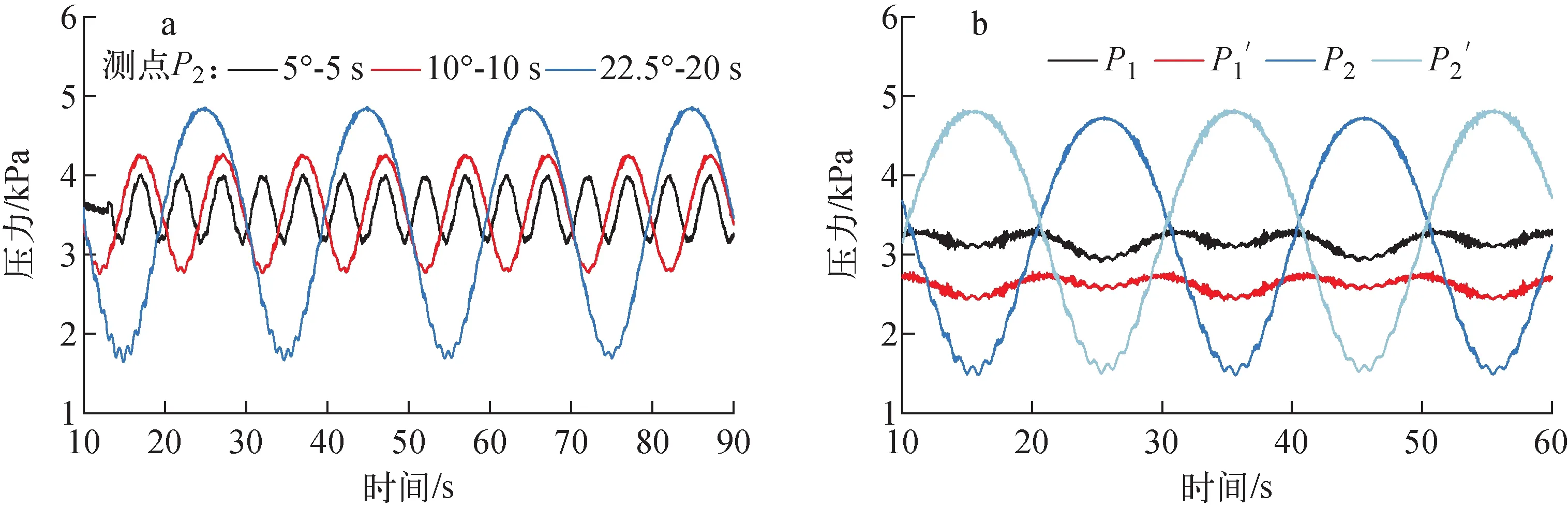
a——运动条件影响；b——测点位置影响图5 摇摆运动压力测量结果Fig.5 Pressure measurement result under rolling motion

摇摆与倾斜条件下70%载液率的压力结果对比如图6所示。由图6a可见，测点P2在22.5°-5 s和22.5°-20 s摇摆条件下的压力振幅与静态倾斜时基本吻合，可依此对摇摆运动模型分析进行相应的简化。由图6b可见，在5°小幅值摇摆时将运动频率提至0.5 Hz，此时壁面附近的自由液面出现水跃和行进波等，压力波动出现明显反馈，即压力振幅明显超出静态倾斜时的压力范围，但其整体压力变化仍呈规律余弦波动，实际工程中可设定测量裕度或偏差因子来覆盖罕发的高频摇摆条件。

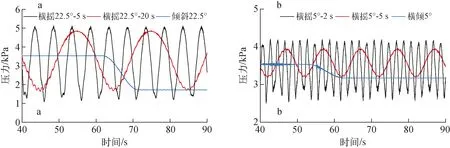
图6 摇摆与倾斜条件下压力结果对比Fig.6 Comparison of pressure results between rolling motion and tilting motion

2.2 水平晃动

水平晃动(横/纵荡)是海洋条件中典型的直线运动，水平晃动过程中壁面阻碍和横向激励引发动势能转化，发生晃荡并产生多种类型的液面波，此时的晃荡过程与运动频率及模型固有频率密切相关。对中压立式储罐晃荡建立等效圆柱腔模型，依据的建模准则[13]为：1) 根据自由液面面积相同确定半径；2) 根据液体体积相同确定圆柱腔内液体高度。通过边界条件、线性液面运动和动力条件求解三维Laplace方程，得到该立式储罐模型自由液面的固有频率：

(1)

式中：ω为晃动(圆)频率；ξ为第一类1阶贝塞尔函数导数根；R为等效半径；H为等效液面高度；g为当地重力加速度。

不同晃动频率下的典型相位图如图7所示。50%载液率条件下，固有频率在1.05 Hz附近；16%载液率条件下，固有频率在0.95 Hz附近。当运动频率小于固有频率时，液面波动较为平缓，当晃动频率接近容器固有频率时，外部激励引发共振，液面破碎并伴随大量液滴飞溅，水中所含气体迸出，产生泡沫。当频率小幅增加后液面形式由平面波变为复杂旋转[14]。以上结果证明了与激励方向垂直模态在晃荡过程中的支配性：当激励频率略大于液体晃动固有频率时，由于外界干扰和初始能量，面外主模态被激发，其与面内主模态相互耦合，产生非平面运动[15]。此时面内波和面外波相位相差90°，晃动波沿内壁顺(逆)时针方向旋转，此时晃荡和抨击现象得到抑制，当激励频率进一步增加，内部流体会彼此来回碰撞，耗散能量，液面呈现整体无序震颤的特征。此外，液面晃荡的演化规律也进一步证实了固有频率理论解析的适用性。

a——0.9 Hz，平面驻波；b——1.0 Hz，水跃破碎；c——1.1 Hz，复杂旋转；d——1.2 Hz，整体震颤图7 不同晃动频率下的典型相位图Fig.7 Typical phase diagram at different swaying frequencies

压力波动时间序列如图8所示，基于测点P2的压力时间序列进一步阐述了不同频率下晃荡现象的演化过程，低频运动时内部流体运动与容器位移之间存在相位差，经过若干个周期，反向流体会在容器中心区域汇合对撞，生成一个压力峰值降低的区间；固有频率邻域内，液面晃荡和模型运动构成典型共振现象，此时压力波动具有明显的双峰结构，第1个波峰为晃荡冲击所致，由于壁面阻碍高速流体微团的动压形成脉冲载荷，其峰值较大且具有强随机性；后一个波峰为惯性所致，流体发生动势能转换沿壁面爬升，且此时上扬的流体处于失重状态，当达到最高点后，下落形成第2个非抨击性波峰且其峰值较小。超过固有频率时抨击导致的压力双峰形式则逐渐消失。

图8 压力波动时间序列Fig.8 Pressure fluctuation time sequence

测点P2不同激励频率下的压力载荷与静压比值如图9所示。由图9可见，在激励频率逐步增加的过程中，测点P2的压力载荷峰值与初始静压比值逐步上升，且在固有频率附近发生阶跃，当激励频率进一步增加至远离共振区域后，该比值缓慢下降，与压力波动和晃荡现象的演化过程均相符。

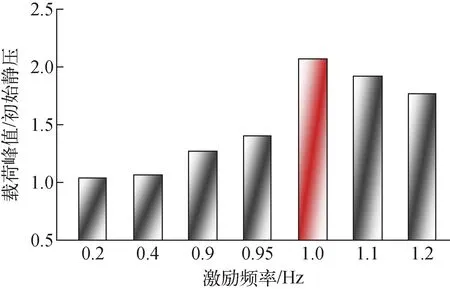
图9 不同激励频率下的压力载荷与静压比值Fig.9 Ratio of pressure load to hydrostatic pressure under different swaying frequencies

通过快速傅里叶变换(FFT)进行频域分析，得到图10所示的频率-幅值曲线。可见，压力波动的振幅主要受到固有频率、运动激励频率和其倍频的支配，在固有频率附近振幅存在显著峰值，且幅度谱由多个连续错杂的波峰构成，压力波动的混沌特性相对明显。

失稳过程和非线性稳态响应如图11所示。可见，压力时序存在失稳过程和非线性稳态响应，这是因为晃荡冲击压力主要受激励频率和固有频率的共同调制。当外部能量输入与内部能量耗散平衡时晃荡达到稳态阶段，即压力波动存在瞬态到非线性稳态的转换过程，在经历失稳过程后液体阻尼将双峰结构抹平且压力振幅限制在固定位置，该现象在载液率较低条件下易发生，且效果明显。根据多维模态分析，初始条件相同时液面波高响应存在不稳定区间，如图12所示，在50%载液率且初始液面静止条件下，重复实验中压力波动后期振幅和相位均有明显差异，即共振频率附近液体晃荡具有随机性的混沌特征，当改变初始液面位置后压力波动的演化过程不同，且在后期数十个周期内两者未能重合，证明该晃动条件下的压力波动具有初值敏感性的混沌特征。

a——16%载液率，20 mm-0.95 Hz晃动；b——36%载液率，20 mm-0.9 Hz晃动图11 失稳过程和非线性稳态响应Fig.11 Instability process and nonlinear steady state response

2.3 耦合运动

实际复杂海况中多种运动激励相互耦合。浮动核电站是小型反应堆技术与船舶工程的有机结合，但其设计和验收标准更为严格，故浮动核电站研究中关于海上多自由度强耦合运动对安全运行的影响问题越来越受到重视，其中典型的耦合形式有横摇-纵摇、纵摇-垂荡以及横摇-纵荡运动。

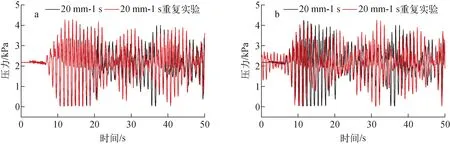
a——初始液面条件相同；b——初始液面条件不同图12 压力波动随机性及初值敏感性Fig.12 Randomness and initial value sensitivity of pressure fluctuation

当横摇同纵摇两种激励完全一致时，耦合运动是特殊的单自由度绕轴(绕x轴与y轴角平分线)运动。横摇与纵摇耦合运动下的压力波动如图13所示，此时4个方位的压力传感器响应基本一致；当横摇激励不同于纵摇激励时，模型在空间内进行复杂耦合运动，此时测点压力成对波动，由于测点P1和测点P′1连线与纵摇中轴垂直，其基本不受横摇的影响，压力波动同纵摇运动规律相符。同理可知测点P2和测点P′2的压力变化主要受横摇激励影响。

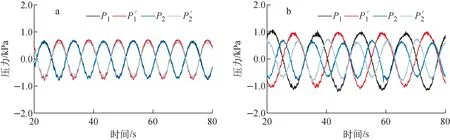
a——横摇10°-10 s+纵摇10°-10 s；b——横摇10°-10 s+纵摇15°-15 s图13 横摇与纵摇耦合运动下的压力波动Fig.13 Pressure fluctuation under coupled motion of rolling and pitching

船舶顶浪航行时，船体会绕其横轴做周期性转动，以及沿其垂直轴的上下往复运动，即纵摇-垂荡运动。垂荡造成压力波动的本质是重力方向附加加速度改变，压力波动和垂荡加速度高度匹配，其振幅受到测点上方水柱高度影响。纵摇与垂荡耦合运动下的压力波动如图14所示。由图14a可见，测点P1在纵摇(10°-10 s)与垂荡(300 mm-5 s)耦合条件下的压力波动与单独纵摇条件下压力波动的差异有限。两者之间的差值远小于重力方向附加加速度的影响。这是由于耦合形式使得各单自由度运动的影响效果非线性叠加，彼此之间存在的相位差会产生强化或削弱的作用。由图14b可知，由于测点P2位于纵摇中轴，纵摇激励对其影响有限，耦合条件下压力变化基本同垂荡一致，即压力波动主要由纵向加速度决定。

图14 纵摇与垂荡耦合运动下的压力波动Fig.14 Pressure fluctuation under coupled motion of pitching and heaving

船体受斜浪或垂直于航向波浪影响时，在向一侧倾斜的同时还有该方向的水平移动，此时即横摆和纵荡的耦合形式。横摇与纵荡耦合运动下的压力波动如图15所示，可见，横摇(10°-10 s)与纵荡(30 mm-2.5 s)耦合条件下，压力变化趋势与横摇运动相符，但局部存在诸多扰动。由图14a可知，耦合条件下测点P1的压力极大值附近出现“凹谷”，这是纵荡影响液面晃动过程进而破坏了中心区域的流体集聚过程，使得压力峰值减小。且摇摆运动受到高频的纵荡影响，压力波动曲线的平滑程度下降。此外，空间位置决定测点P1在纵荡条件下受液面波动和流体动压的影响较小，压力波动相对微弱。由图14b可见，测点P2的压力波动幅值与单独横摇条件下基本一致，但压力不再按规律的正余弦形式变化，横摇激励同纵荡造成的液面颤动互相影响后发展成一特定规律，在完整周期内，测点压力近似S型曲线上升后线性递减。

图15 横摇与纵荡耦合运动下的压力波动Fig.15 Pressure fluctuation under coupled motion of rolling and swaying

3 结论

本文依托六自由度运动平台开展了安注水箱晃荡实验，基于可视化测量和时频域分析，研究了典型海洋条件下的液面晃荡特征和压力波动规律。通过本文研究可得到如下结论。

1) 摇摆运动条件下，液面晃动形式为平面驻波和边缘水跃，测点的压力波动规律受运动激励和测点位置影响呈规律的正余弦变化，在考虑安全裕度的基础上可基于此对海洋条件系统分析模型进行合理简化。

2) 水平晃动条件下，压力振幅主要受固有频率、激励频率及其倍频支配，在共振邻域附近，随着激励频率的加剧，自由液面存在旋转和震颤等非平面波结构。压力时间序列存在失稳演化过程和混沌区间，在装备设计中可改进结构设计使其固有频率远离外部激励等危险频率。

3) 耦合运动条件下，测点压力受各单自由度运动规律及其耦合形式影响，压力波动序列存在彼此增强或削弱的区间，在考虑各运动间相位差的基础上可对耦合运动拆解分析。

本文研究可为工程设计提供较直观的分析和判断依据。