车载运动条件下铅铋堆LESMOR热工安全特性分析
陆定晟,魏诗颖,王成龙,*,田文喜,苏光辉,秋穗正
(1.西安交通大学 核科学与核技术学院,陕西 西安 710049;2.中广核研究院有限公司,广东 深圳 518000)
“十四五”规划指出我国将继续推行能源结构优化,并将重点建设模块式小型堆[1]。现有小型模块化反应堆(SMR)设计多以商业发电为用途,在机动性和灵活性方面存在一定的限制。为满足特殊任务能源供给需求,更具机动灵活性的车载超小型模块化反应堆(very small modular reactor,vSMR),受到了核能强国的广泛关注。美国分别采用空间热管堆KILOPOWER技术与氦气冷却技术研发可实现车载运输的MEGAPOWER和HOLOS系统[2-3]。韩国采用超临界二氧化碳冷却技术研发了车载一体化紧凑型微堆KAIST MMR[4]。国内中科凤麟团队结合铅冷快堆(LFR)研发了超小型移动式先进核能系统“核电宝”[5]。
LFR是目前SMR的主力堆型,也是有望最早实现工程示范的堆型。西安交通大学结合SMR固有特点并基于LFR小型化研究经验提出车载铅铋快堆LESMOR(lead-bismuth small modular reactor)系统方案,满足物理热工设计准则,具有良好的固有安全性。然而在实际运行时,车载反应堆系统会存在多自由度空间运动,这些运动形式将影响系统的自然循环能力以及热工水力特性。目前有关运动条件下的反应堆特性研究大多针对海洋条件。高璞珍等[6]通过建立海洋摇摆条件下冷却剂流动数学物理模型,分析附加惯性力对冷却剂的影响。Chang等[7]实验探究了海洋摇摆条件下运动周期与流量波动周期的一致性,并指出附加惯性力影响流量波动行为。不同于海洋条件下船体摇摆运动的影响显著,影响反应堆系统的车辆行驶运动尚不明确。铅铋快堆瞬态热工水力分析程序LETHAC比较了来自KYLIN-II 61棒绕丝束实验,相关性的误差均在2%以内。此外,通过TALL瞬态试验证实了LETHAC的瞬态计算能力[8]。因此本文将基于车载铅铋快堆LESMOR,运用铅铋快堆瞬态热工水力分析程序LETHAC[9-15],展开LESMOR自然循环热工水力及安全特性的计算分析。探究车载运行过程中对反应堆系统造成影响的运动工况,获得不同运动条件下LESMOR系统内冷却剂流量、温度等关键参数的变化规律。
1 车载运动条件非惯性系动量方程
车载核能系统在路面上行驶时,受道路条件影响,车体会产生复杂的运动形式。在汽车动力学中,按坐标系把整体问题分成局部问题,如图1[16]所示,x0、y0和z0为描述车辆运动时的固定坐标系。xA、yA和zA是固定在车身的坐标系,令其原点在车身重心SPA上,车身绕xA轴的转动称为侧倾运动kA,绕yA轴的转动称为俯仰运动φA,绕zA轴的转动称为横摆运动ψA。研究车辆行驶对反应堆系统内热工水力参数的影响时,考虑的汽车运动主要分为3类,即:1) 沿x0方向的直线行驶;2) 与x0方向垂直的运动,包括在y0方向上的横向运动(侧偏)和绕铅锤轴的转动(横摆);3) 在表面不平整的道路上行驶,考虑沿铅锤轴的跳动,以及绕横轴和纵轴的角运动(俯仰和侧倾)。

图1 描述车辆运动的坐标系及其名称Fig.1 Coordinate system describing movement of vehicle and its name
为便于分析运动条件所带来的影响,选择固定在车体上的坐标系对堆内流体进行受力分析,固定在车体上的坐标系相对于地面惯性系具有加速度,称为非惯性系。假设非惯性系(车体)(o-xA-yA-zA)相对于地面的惯性系(o-x0-y0-z0)同时做平动和旋转运动,平动速度为u0,转动角速度为ω,如图2所示。流体质点在非惯性坐标系(o-xA-yA-zA)中的位置矢量是r,在惯性系(o-x0-y0-z0)中的位置矢量则是r+r0,r0则是连接惯性系原点(o0)与非惯性系原点(o)的矢量。

图2 非惯性参考系Fig.2 Non-inertial reference frame
非惯性系下流体的动量方程为:
(1)
相应地,运动条件的附加力为:
(2)
式中:ur为流体质点在非惯性系(o-xA-yA-zA)中的速度,m/s;f为体积力矢量;a0为平动加速度;2ω×ur为科里奥利加速度(简称科氏加速度);ω×(ω×r)为向心加速度;(dω/dt)×r为切向加速度。
所开发的铅铋快堆系统程序LETHAC为一维程序,所采用一维单相守恒方程分别如下。
质量守恒方程:
(3)
动量守恒方程:
(4)
能量守恒方程:
(5)
式中:ρ为流体密度,kg/m3;W为质量流量,kg/s;A为流通面积/m2;p为压力,Pa;f为摩擦系数;De为等效直径,m;g为重力加速度,m/s2;h为冷却剂焓,J/kg;Uh为加热周长,m;z为轴向坐标,m。
液态铅铋合金流动压降采用常规牛顿流体的流动压降公式进行计算,沿程摩擦阻力压降采用达西(Darcy)公式并分别对圆管和棒束通道的摩擦阻力系数进行讨论选取:
(6)
式中:Δpfric为摩擦压降,Pa;L为流道长度,m。
液态铅铋合金的换热关系式一般整理成无量纲数——Pe的关系式。式(7)中,右边第1项和第2项分别代表导热和对流的效果。
Nu=a+bPec
(7)
式中,a、b和c均为常数。
Pe=Re·Pr
(8)
并对单相液态铅铋合金流经不同几何形状通道时传热关系式进行总结。在程序中保留的一些液态金属在圆管和棒束中的换热关系式[8]列于表1、2。

表1 圆管中液态金属换热关系式Table 1 Liquid metal heat transfer relationship in circular tube

表2 棒束中液态金属换热关系式Table 2 Liquid metal heat transfer relationship in rod bundles
考虑铅铋共晶合金LBE(lead-bismuth eutectic)流体的一维流动特性,动量方程可改写为:
(9)
针对不同的车载运动条件,分别在LETHAC程序中添加相应的运动条件附加力模型,从而实现对不同运动条件下移动式铅铋核电源的瞬态热工水力特性进行求解。
2 车载运动条件数学物理模型
2.1 直线行驶/侧偏
直线行驶为沿xA方向的直线运动,如图3a所示,车体沿前进方向以加速度a=a(t)i作直线运动,匀速运动时a=0,不考虑转动(ω=0),重力加速度矢量f=-gk。
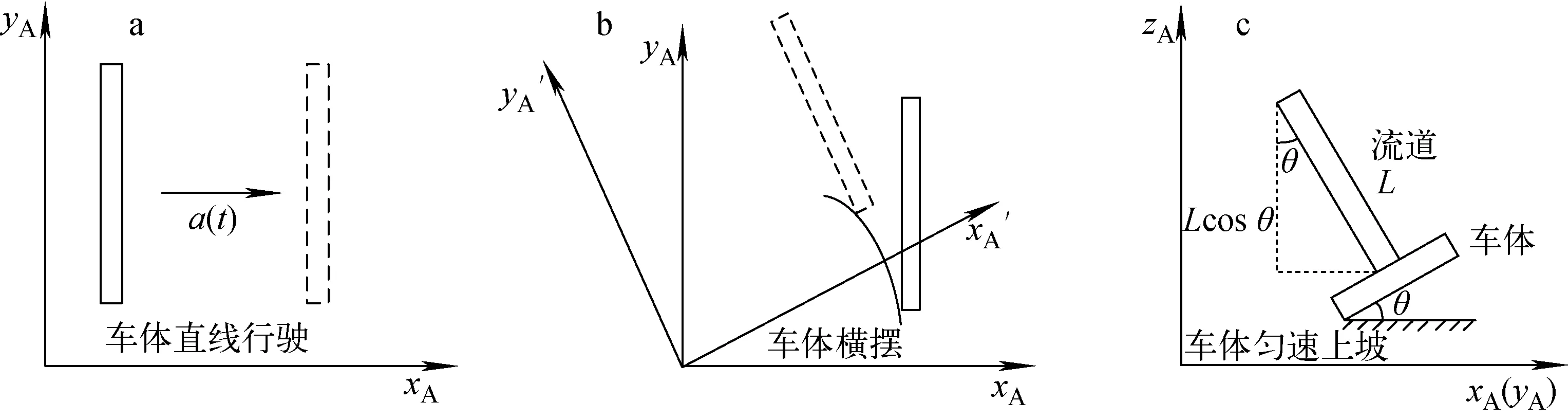
图3 车体行驶运动示意图Fig.3 Diagram of car body driving motion
故运动条件附加力为:
F·k=-ρa0·k=-ρa(t)i·k=0
(10)
运动条件对液态铅铋的影响为:
(F+ρf)·k=-ρg
(11)
因此,沿xA方向的直线行驶时,附加力沿流动方向分力为0,对流体无直接影响。侧偏运动为在yA方向上的横向运动,与沿xA方向的直线行驶类似,对流体无直接影响。
2.2 横摆
横摆为绕铅锤轴zA轴的转动,如图3b所示。不考虑xA、yA和zA方向的加速度(a=0),以逆时针为正方向,摆动角速度ω=ω(t)k,重力加速度矢量f=-gk。
故运动条件附加力为F·k=0,运动条件对液态铅铋的影响为(F+ρf)·k=-ρg。与直线行驶和侧偏运动相同,运动条件对冷却剂流动无直接影响。
2.3 俯仰/侧倾
车辆的俯仰运动主要体现在坡道行驶上,可归纳为绕yA轴作某一角度的倾斜运动,如图3c所示。不考虑xA、yA和zA方向的加速度(a=0)和绕xA轴,yA轴和zA轴的摆动(ω=0),重力加速度矢量为:f=-g·cosθk+g·sin θi(j)。
故运动条件附加力为:
F·k=0
(12)
体积力分量为:
ρf·k=-ρgcosθ
(13)
因此运动条件对液态铅铋的影响为:
(F+ρf)·k=-ρgcosθ
(14)
侧倾和俯仰类似,只是侧倾为绕yA轴作倾斜。侧倾条件下的运动条件附加力可参考俯仰条件。
2.4 垂直振动
垂直振动为车体沿zA轴的周期性跳动,可认为车体在zA方向引入一个周期性的加速度,即a=a(t)k,如图4a所示。不考虑其他方向的运动和摆动(ω=0),重力加速度矢量为f=-gk。
在接种疫苗的过程中,护士应密切关注儿童的具体情况,观察其是否出现汗出、心慌、头晕、发热、面色苍白等不良反应,如出现上述情况,应立即通知医生,给予妥善处理。
故运动条件附加力为:
F·k=-ρa·k=-ρa(t)
(15)
运动条件影响为:
(F+ρf)·k=-ρ(a(t)+g)
(16)

图4 车体振动运动示意图Fig.4 Diagram of vibration motion of car body
2.5 俯仰振动
俯仰振动时通道内流体质点位置为r=xi+yj+zk,流体质点在非惯性系中的速度为ur=u(t)k,重力加速度矢量为f=-g·cosθx(t)k+g·sinθx(t)j,故:
柯氏力:
2·ω×ur=2·ω(t)j×u(t)k=
-2·ω(t)·u(t)i
(17)
离心力:
ω×(ω×r)=-ω2(t)xi-ω2(t)zk
(18)
惯性力:
(19)
因此运动条件附加力为:
(20)
体积力分量为:
ρf·k=-ρgcosθx(t)
(21)
运动条件影响为:
(22)
2.6 垂直振动耦合俯仰振动
结合上述两种运动条件,如图4c所示,由于存在摆动角a=a(t)cosθx(t)k+a(t)sinθx(t)j。
故运动条件附加力为:
(23)
运动条件影响为:
(24)
(25)
3 车载铅铋快堆LESMOR系统
西安交通大学结合SMR固有特点并基于LFR小型化研究经验提出了5 MWt、寿期15 a、反应堆高度3.2 m、可用卡车装载、可双模式运行的车载铅铋快堆LESMOR系统方案,如图5的LESMOR系统整体布置图。该系统采用双模式运行机制,在汽车运行过程中采用低功率自然循环运行模式,在静止时采用满功率强迫循环运行模式,两种模式的运行参数列于表3。
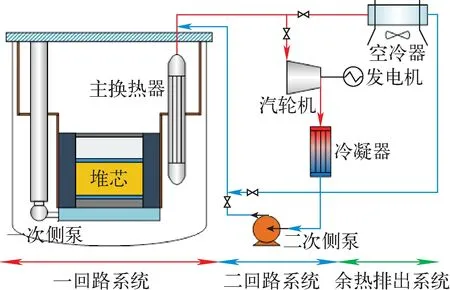
图5 LESMOR系统整体布置图Fig.5 Overall layout of LESMOR system

表3 LESMOR双模式稳态运行参数Table 3 LESMOR dual-mode steady-state operation parameter
LESMOR采用的结构材料为T91,T91在铅铋中可承受的温度为550 ℃,使用合适的涂层则可达到650 ℃,出于保守设计的考虑,采用550 ℃作为包壳的热工设计限值温度。此外,燃料中心峰值温度必须低于燃料材料的熔化温度。LESMOR采用的核燃料为UN燃料,该燃料可耐受1 700 ℃的高温运行,故芯块的安全温度定位1 700 ℃。
4 车载运动条件对系统瞬态特性的影响
4.1 坡道行驶
我国公路工程技术标准规定,最大坡度范围为3%~9%[17]。为探究坡道行驶对系统瞬态特性影响,故计算稳定运行100 s后坡度5%~50%工况。
图6~8为不同坡度对LESMOR系统流量和温度的影响。当倾斜发生时,由于驱动压头瞬间减小,堆内流量迅速下降,且随着坡度增大,堆芯流量下降幅度增大。当坡度达到50%时,堆芯流量最低降为358.5 kg/s,变化幅度达8%,此时冷却剂出口温度385.4 ℃,包壳和燃料峰值温度分别为411.3、442.4 ℃,均低于瞬态安全限值。在倾斜发生约150 s后,铅铋回路会重新建立稳定的自然循环。稳定时,坡度50%下流量下降幅度约为5%。在计算范围内,堆芯进出口温度差、包壳温度和燃料温度均随坡度增大而略有增大,当坡度达到50%时,包壳和燃料峰值温度分别为409.0 ℃和440.3 ℃,相对于稳态值增加了约2 ℃,处于瞬态安全限值内。因此在汽车正常行驶的坡度范围内,坡度对系统自然循环产生的影响较小,系统流量和温度变化幅值较小,LESMOR系统可平稳安全地运行。
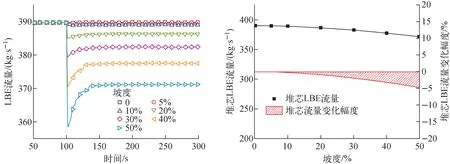
图6 坡道行驶时堆芯LBE流量变化Fig.6 Change of core LBE flow during ramp driving
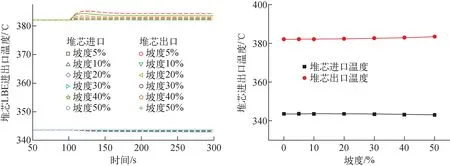
图7 坡道行驶时堆芯冷却剂进出口温度变化Fig.7 Core coolant inlet and outlet temperatures during ramp driving

图8 坡道行驶时包壳及燃料温度变化Fig.8 Ramp cladding and fuel temperatures during ramp driving
4.2 垂直振动
垂直振动在zA方向给液态铅铋引入了周期性的附加力,故分别展开相同周期、不同加速度工况计算(振动周期10 s,加速度振幅0.1g~0.5g)以及相同加速度、不同振动周期工况计算(加速度振幅0.3g,振动周期5~25 s)。
垂直振动在zA方向给液态铅铋引入了周期性的附加力,使得驱动压头呈现周期性变化,在该驱动压头下,系统流量也呈现周期性变化,进而导致系统内的摩擦阻力和局部阻力周期性变化。图9为堆芯流量和作用力瞬态响应。图10为堆芯LBE流量随加速度变化。由图9可知,由于阻力变化响应的滞后,在加速度为正时驱动力大于系统阻力,流量增加;加速度为负时,驱动力下降速度大于阻力下降速度,流量减小。而流量增加时,阻力系数增加,故流量向上的振幅略小于流量向下的振幅,堆芯流量为非等幅震荡。此外,图9a和图10显示,流量波动幅度随加速度振幅的增大而增大。当加速度振幅达到0.5g时,流量最大降为273.1 kg/s,下降幅度达约30%。由于阻力的影响,堆芯流量为非等幅震荡,因此平均流量相较于稳态时的流量,会向下产生一定的偏移,且加速度越大,流量均值相较于稳态流量值减少幅度越大。
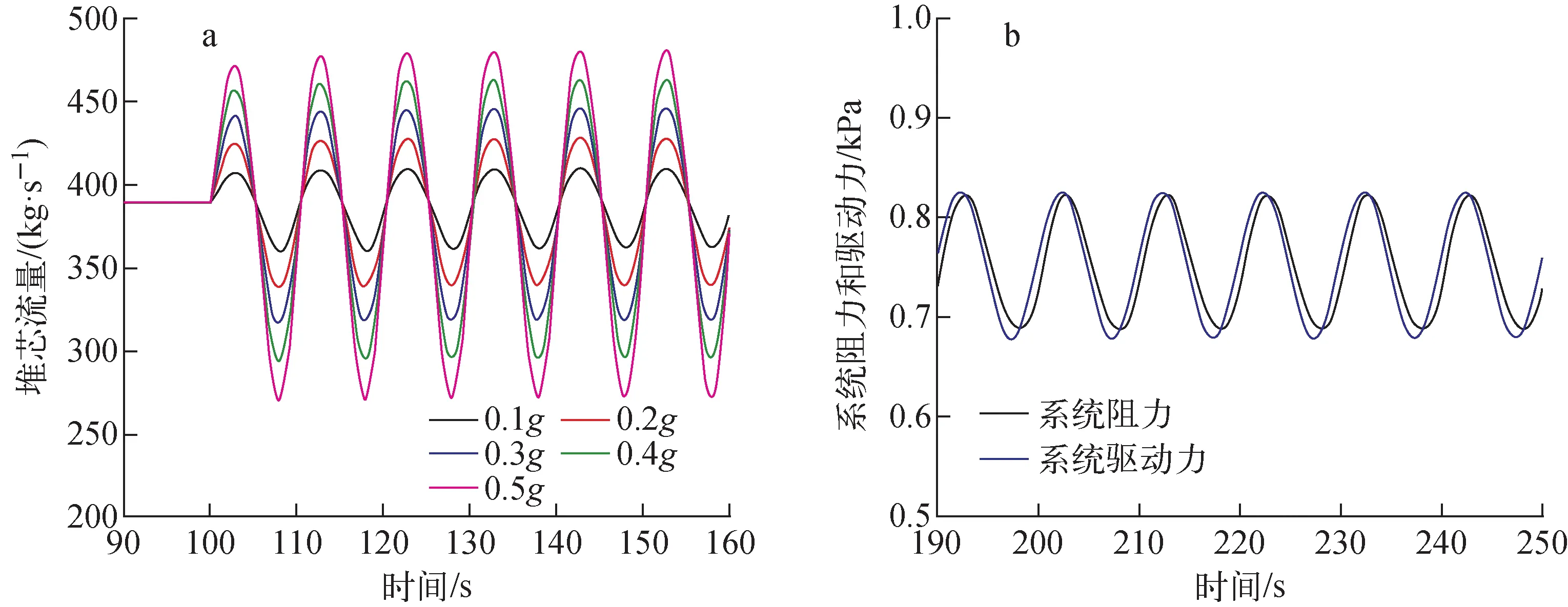
图9 堆芯流量和作用力瞬态响应Fig.9 Transient responses of core flow and force
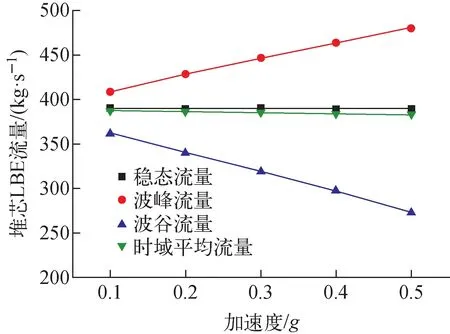
图10 堆芯LBE流量随加速度变化Fig.10 Core LBE flow vs. acceleration
图11为相同周期、不同振幅下堆内温度的瞬态响应。流量的波动将引起堆芯冷却剂进出口温度波动,尤其是堆芯出口温度,堆芯入口温度由于换热器的作用无明显波动。包壳和燃料峰值温度随着冷却剂温度的波动而呈现相同的波动规律。在稳定波动状态下,加速度为0.5g时,包壳和燃料峰值温度波动幅度最大,最高值分别达410.2、440.7 ℃,远低于一般瞬态的安全限值(包壳限值为650 ℃,燃料安全限值为1 700 ℃)。图11表明,周期改变对流量波动的幅度影响不明显,不同周期下,冷却剂流量的波峰、波谷相差不大,时域平均流量保持持平,略低于稳态流量。图12为相同振幅、不同周期下堆芯流量变化。图13为相同振幅、不同周期下堆内温度的瞬态响应。因流量波动引起的堆芯出口温度产生波动,且随着周期的增加,温度变化幅度越大。同样,入口温度由于换热器的作用,无明显波动。燃料包壳温度和燃料中心温度在冷却剂温度的作用下,呈现同样的波动规律。在周期为25 s时,温度波动幅值最大为±3 ℃,包壳和燃料峰值温度分别达410.8 ℃、441.6 ℃,均低于一般瞬态安全限值。

图11 相同周期、不同振幅下堆内温度的瞬态响应Fig.11 Transient response of temperature in reactor with the same period and different amplitudes
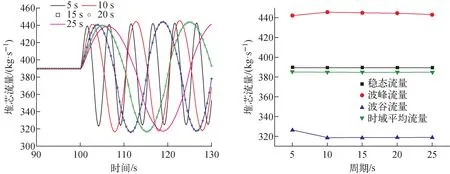
图12 相同振幅、不同周期下堆芯流量变化Fig.12 Core flow with the same amplitude and different periods
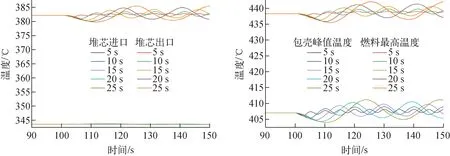
图13 相同振幅、不同周期下堆内温度的瞬态响应Fig.13 Transient response of temperature in reactor with the same amplitude and different periods
4.3 俯仰振动
同垂直振动工况,分别展开相同周期、不同最大俯仰角(俯仰周期15 s,俯仰角度5°~30°),及相同俯仰角、不同周期(俯仰角度10°,俯仰周期10~20 s)计算。
LESMOR系统中心对称布置了4台主换热器,图14为LESMOR系统中关于yA轴对称的两台换热器的流量波动情况。由图14可见,关于yA轴对称的换热器流量具有相同的波动效果,但为反相位,因此在堆芯处叠加后,堆芯流量波动幅值较小,如图15a所示。随着俯仰角度的增大,系统自然循环流量波动幅度增加。同垂直振动类似,由于阻力的影响,流量的波动为非等幅震荡,向下的振动幅度大于向上的振动幅度。在俯仰角度为30°时,换热器内波谷流量达到48 kg/s,变化幅度为51.6%。堆芯流量向下振幅达39 kg/s,变化幅度为10%,可见,由于系统布置的原因,俯仰振动对各换热器影响大于对堆芯的影响。此外,如图15b和图16所示,俯仰角度增加,系统时域平均流量下降,下降幅度达4.52%。

图14 不同俯仰角度下换热器流量瞬态响应Fig.14 Transient response of heat exchanger flow at different pitching angles

图15 相同周期、不同俯仰角度下堆芯冷却剂流量变化Fig.15 Core coolant flow rate under the same period and different pitching angles
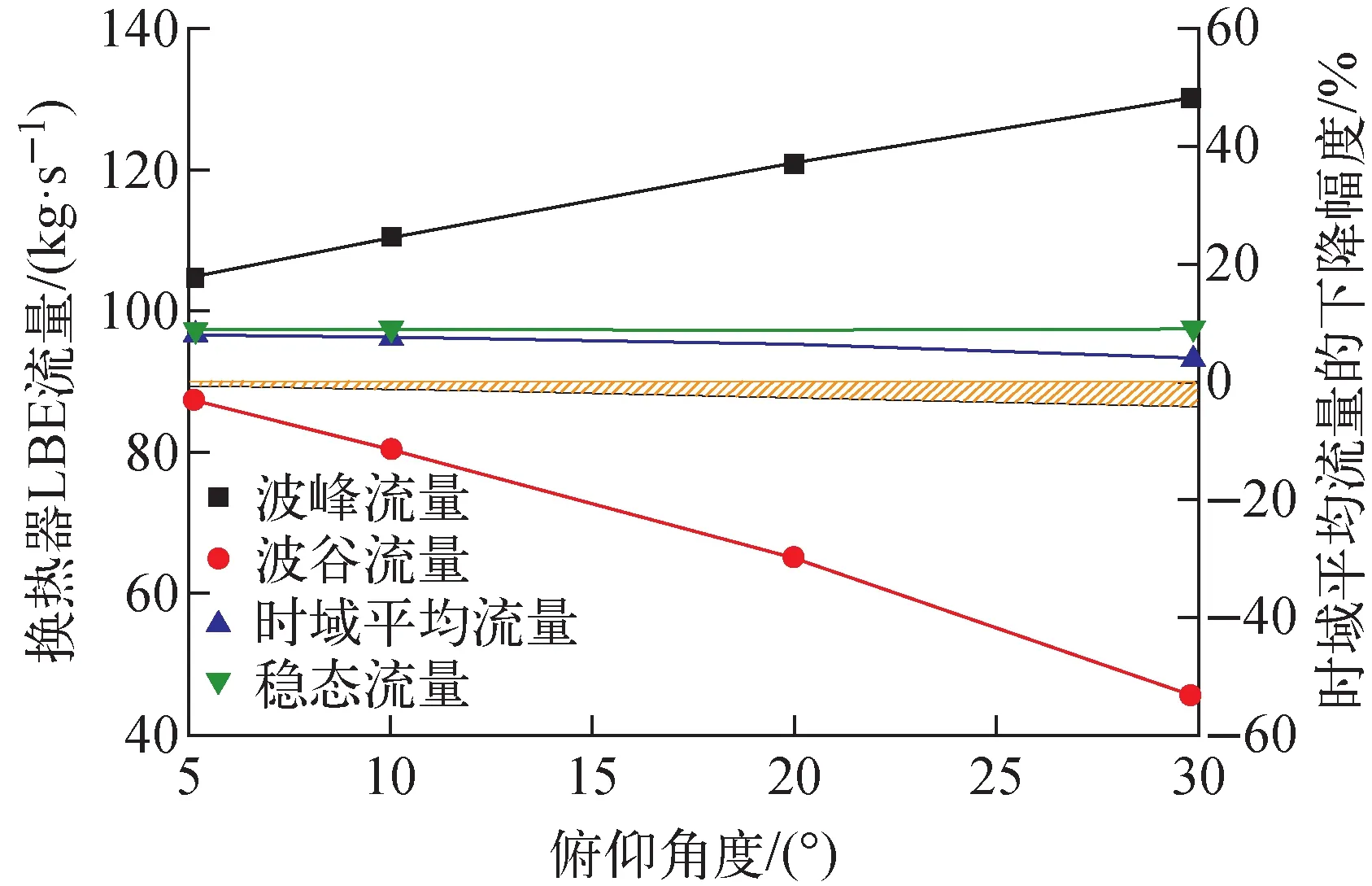
图16 不同俯仰角度下换热器流量变化Fig.16 Flow rate of heat exchanger at different pitching angles
图17为相同周期、不同俯仰角度下堆芯内温度的瞬态响应,由于流量波动幅度较小,故堆芯温度变化幅度也较小。倾斜角30°时,包壳和燃料峰值温度最高升高约3 ℃,分别为410 ℃和441 ℃,远低于瞬态运行安全限值。图18为相同俯仰角度、不同俯仰周期下堆芯和换热器流量的波动情况。俯仰角度为10°,周期为10~20 s。相同俯仰角度下,周期增大,流量波动幅值减小,这是因为周期增大,附加力减弱,流量波动的非对称性减弱,波动幅值减小。图19为相同俯仰角度、不同俯仰周期下堆芯及燃料元件温度的变化。由于俯仰振动对堆芯流量的影响较小,故对堆芯内温度的影响也较小。相对于稳定值,冷却剂温度、包壳峰值温度和燃料中心最高温度的变化幅值在2 ℃以内。
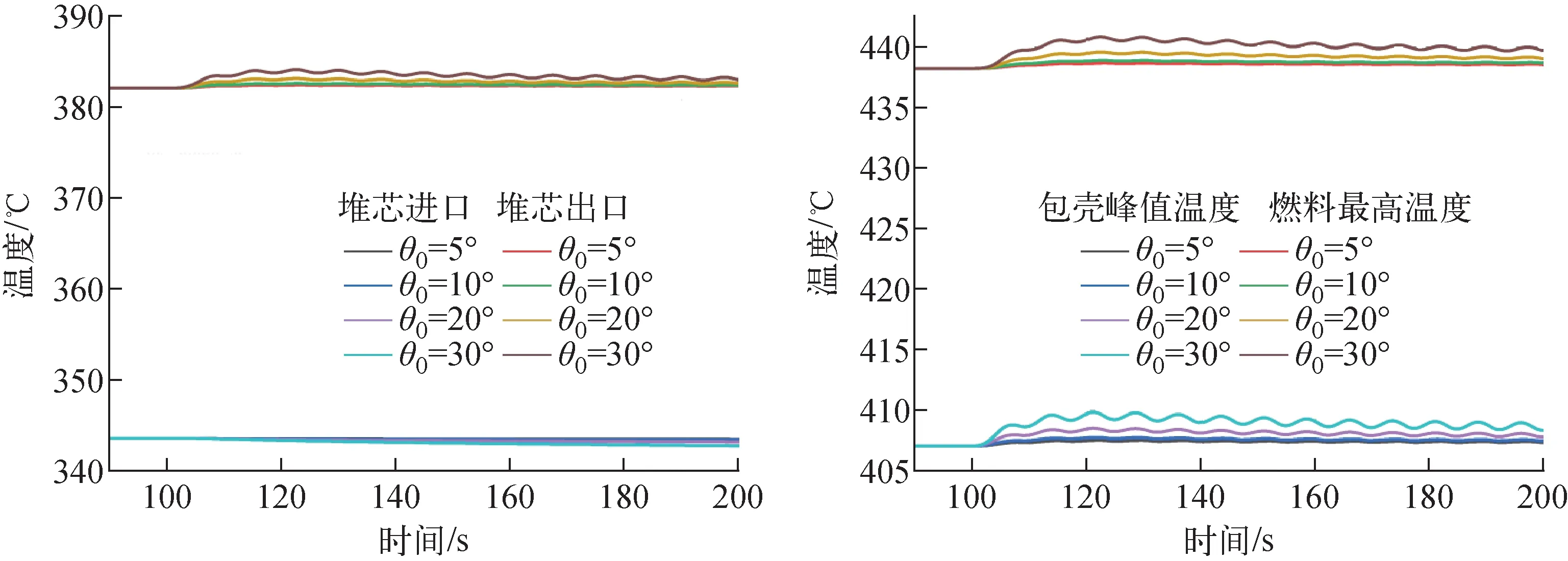
图17 相同周期、不同俯仰角度下堆芯内温度的瞬态响应Fig.17 Transient response of core temperature under the same period and different pitching angles
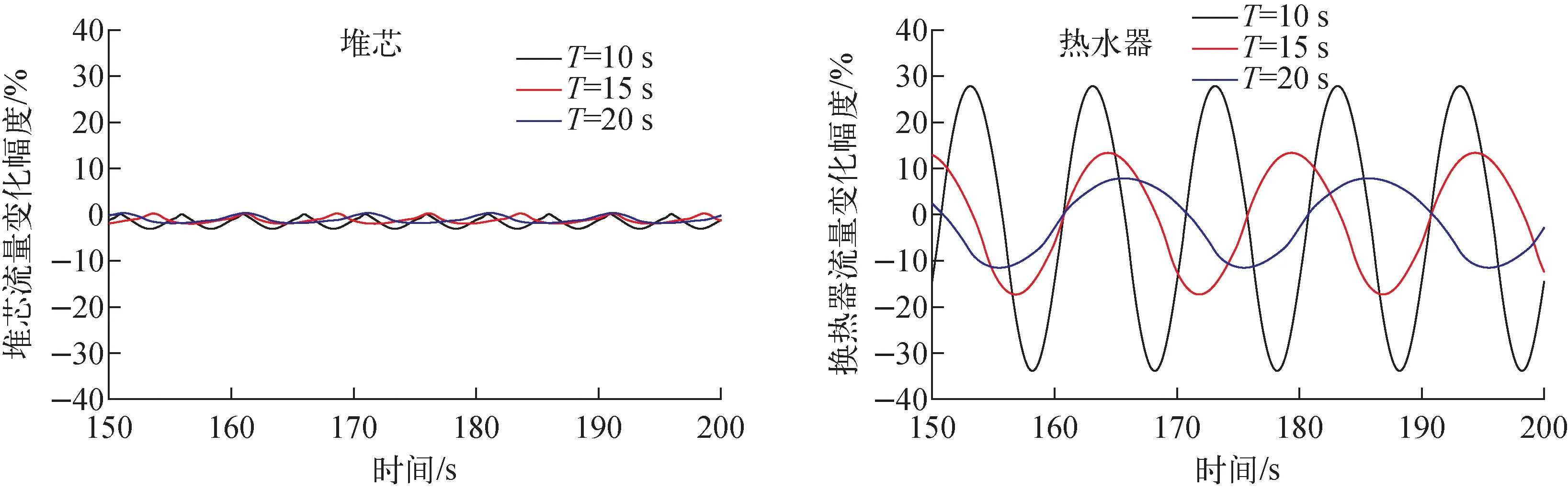
图18 不同俯仰周期条件下堆芯和换热器内冷却剂流量变化Fig.18 Coolant flow rates in core and heat exchanger under different pitching periods
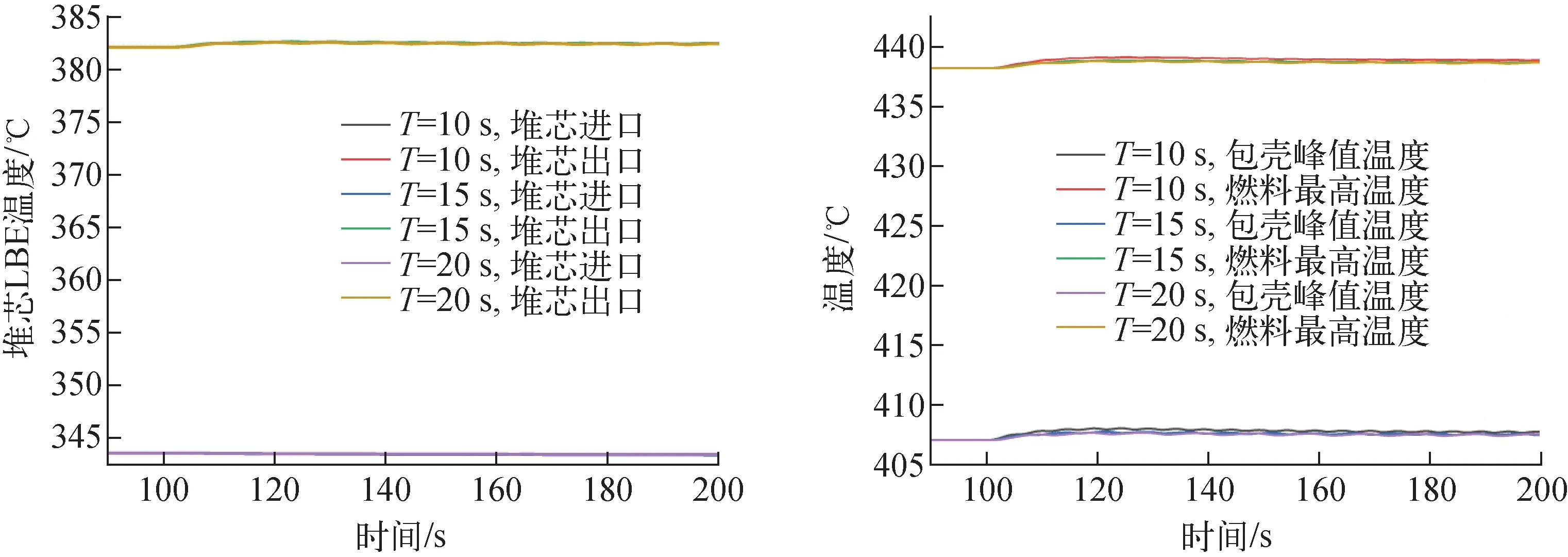
图19 相同俯仰角度、不同俯仰周期下堆芯及燃料元件温度的变化Fig.19 Temperatures of core and fuel element under the same pitching angle and different pitching periods
4.4 垂直振动与俯仰振动耦合
考虑垂直振动与俯仰振动耦合运行条件影响,对俯仰角度20°、俯仰周期20 s、垂直振动加速度0.3g、振动周期5~15 s耦合工况展开计算。耦合运动条件下,系统流量的波动情况如图20所示,两种运动条件周期和初始相位决定了对系统流量的影响(同相或异相)。当两类运动的影响为同相时,系统自然循环流量波动幅值增大;反之异相时,则幅值减小。由于换热器为yA轴对称布置,在俯仰条件下,沿yA轴对称的换热器流量波动为异相,故流量叠加后对堆芯流量的影响较小,因此俯仰和垂直振动耦合的情况下,垂直振动对堆芯流量的影响占主导地位。

图20 俯仰和垂直振动耦合条件下堆芯的流量变化Fig.20 Core flows under pitching and vertical vibration coupling conditions
由前述单一运动条件分析可知,垂直振动和俯仰振动会导致系统时域平均流量下降,耦合条件下同理。因此,堆芯出口冷却剂时域平均温度略有升高,如图21所示,相对于稳态值,包壳和燃料峰值温度最大变化幅度约为3 ℃。包壳峰值温度和燃料中心最高温度依然远低于安全限值。
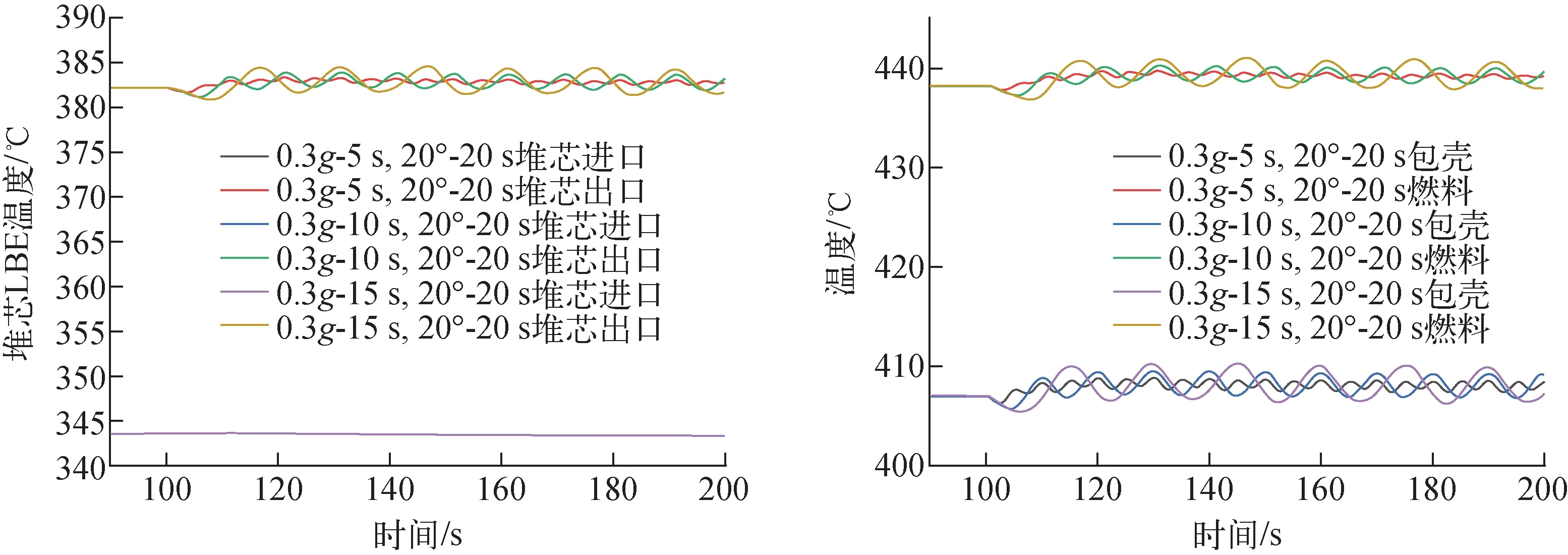
图21 俯仰和垂直振动耦合条件下堆芯冷却剂温度和燃料元件温度变化Fig.21 Core coolant temperatures and fuel element temperatures under pitching and vertical vibration coupling conditions
5 结论
本文通过对车辆运行的运动工况进行梳理,基于非惯性系下动量方程的推导,建立运动条件附加力模型,分析了运动条件对液态铅铋的影响。展开了对反应堆流体造成影响的运动工况下LESMOR自然循环热工水力及安全特性分析。
研究表明,坡道行驶、垂直振动、俯仰振动及垂直耦合俯仰振动运动工况下,LESMOR系统自然循环流量显著下降且堆芯内包壳和燃料温度显著上升。极限工况下,系统自然循环流量瞬态下降幅度不超过30%,包壳和燃料瞬态温度最高达411.3、442.4 ℃,上升不超过4 ℃,远低于瞬态运行安全限值。因此LESMOR系统在汽车正常行驶和可能出现的极限行驶范围内都能保持稳定安全运行。但需注意在俯仰振动条件下换热器内的流量波动,避免出现局部过冷凝固现象。

