基于图像噪声源的单粒子布朗运动模拟

杨凯宁，李井源，孟群康，江先阳，王晓峰

（武汉大学a.物理科学与技术学院；b.物理国家级实验教学示范中心，武汉 430072）

0 引言

自然界中有许多随机现象，人们尝试了解和计算这些随机现象的统计规律，将这些随机现象应用于通信安全［1］和芯片加密［2］等领域。本实验研究的图像噪声，是指存在于图像数据中不必要或多余的干扰信息，其通常表现为引起较强视觉效果的孤立像素点或像素块［3］。噪声可以描述为“不可预测的，只能用概率统计方法来认识的随机误差”。对于噪声的去除往往用一定的算法来实现。目前图像去噪的通常算法有变换域去噪算法，即将二维图像信号通过傅里叶分析等方法变换到频率域中，再利用噪声的高频特性将其滤除［4］。

布朗运动，作为人类最早认识微观世界的契机，苏格兰植物学家罗伯特·布朗发现水中的花粉及其他悬浮的微小颗粒不停地作不规则运动。1877 年，Delsaulx［5］提出，布朗运动的原因是微小颗粒受到周围分子不平衡的碰撞而导致的运动。1905 年，爱因斯坦发表了关于布朗运动理论的论文，布朗运动成为分子运动论和统计力学的基础［6］。对于布朗运动的展示，常用显微镜直接观察花粉在液滴内的运动，由于花粉布朗运动是随机的分子热运动，其具有快速、随机、大范围的特点，难以完全复现；大多数科技馆中的布朗运动演示仪是利用伪随机数电控小球进行撞击，仅仅演示出类似随机的现象，并不是真正的随机现象。为克服布朗运动难以测量和演示的困难，在实验中设计了基于图像噪声的随机源，并利用现场可编程逻辑门阵列（Field Programmable Gate Array，FPGA）驱动小车模拟单粒子的布朗运动，其使用简便、直观，具有较高的测量准确度。

1 实验原理

1.1 布朗运动

用显微镜观察液面悬浮的微粒，当微粒足够小时，受到来自各个方向的液体分子撞击作用是不平衡的。当微粒在某一个方向受到撞击作用较强时，致使微粒又向其他方向运动，这样就引起了微粒的无规则的运动。这种被分子撞击的悬浮微粒做无规则运动的现象，称为布朗运动［7］。

爱因斯坦建立的布朗运动扩散理论［8］，考虑了布朗粒子的一维无规则运动，粒子每隔r时间被撞击一次移动的距离为l，每次撞击后向左和向右运动的可能性各占一半。假设粒子从原点出发，在时刻t粒子已受到了n＝t／r次撞击。爱因斯坦指出：粒子的平均位移为零，均方位移与时间成正比，即

式中，D为扩散系数。

本实验利用图片噪声生成随机数控制小车进行一维和二维运动，在宏观上模拟布朗运动。

1.2 图像噪声的提取

（1）噪声产生。图像噪声分为外部噪声和内部噪声。外部噪声指系统受外部环境的干扰，以电磁波的形式进入系统内部而引起的噪声；内部噪声是指图像采集设备中的电子元件产生的噪声，器件中电子或空穴的随机性热运动产生的噪声，以及光传播过程中光量子密度受气体分子的散射产生的光量子噪声。所有噪声最终叠加在生成的图像中，表现为一种随机的二维高频噪声［3］。

（2）小波法提取噪声。小波变换是一种能对时间或空间频率的局部化分析，通过伸缩平移运算对信号逐步进行多尺度细化，能自动适应时频信号分析的要求，从而可聚焦到信号的任意细节的数据分析算法［9-10］。二维数据的小波变换的定义如下：

令f(x1，x2) ∈L2（R2）为一个二维信号，x1、x2分别为其横、纵坐标；ψ（x1，x2）为二维基本小波。

正变换和逆变换分别为

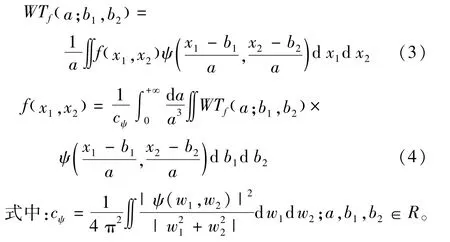
利用基本的二维小波变换对图像的二维信号作两级多分辨率分析，经过正变换之后通过临界阈值截断的部分，其逆变换结果即为图像中的噪声信号［3，10-12］。

处理步骤主要分为灰度化、两级小波变换、噪声提取和随机性优化。灰度化是将图像的RGB 信息转化为灰度信息，设定灰度值为0～255；两极小波变换是将灰度化后的图像去噪；噪声提取是对原灰度图像和去噪后的图像的灰度值求差，并将此差值的中间量偏移128，产生噪声图像；随机性优化是将噪声图像网格化为多个4 ×4 的灰度值矩阵，每个灰度值矩阵在相同位置取出一个元素组成优化后的噪声图像，目的是减少图像相邻像素点之间的关联性。

（3）小波法与高斯法噪声提取效果对比。本研究利用Matlab中小波函数sym4 对原图［图1（a）］进行2层小波变换去噪，再将噪声对应的小波变换参数进行逆变换，得到的结果为小波法提取出噪声图像［图1（b）］。

作为对比，利用Matlab 中的高斯滤波函数gausFilter做类似噪声提取处理，得到的噪声图像如图1（c）所示。

图1 噪声提取算法的对比

可见，高斯法得到的噪声图明显保留了一部分原图的信息，而小波法得到的噪声图基本去除了原图信息的影响［14］。

1.3 随机数的产生

取出噪声图像中每个像素点的灰度值，将灰度值数据转换为二进制随机数。统计噪声图片中每个像素点的灰度值出现的个数，绘出直方图（见图2），像素点灰度值分布呈现出数学期望μ 为128 的高斯分布，即提取出来的噪声为随机噪声。

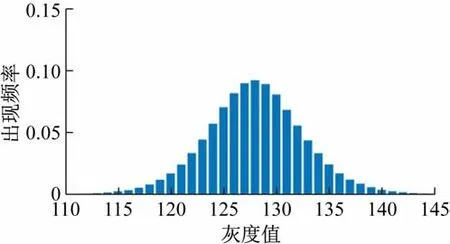
图2 噪声图像灰度值分布统计图

将灰度值转换为二进制随机数。以灰度中值128作为临界值，将灰度二值映射为0 和1，以实现二进制随机数的产生。

1.4 小车对布朗运动的模拟

（1）小车模拟粒子作一维布朗运动。将20 bit二进制随机数作为小车一维运动一次的指令，其中最高位控制前后方向，余下位控制小车每次所走的路程。小车每次所走的路程与控制位的关系：

（2）小车模拟粒子作二维布朗运动。将20 位二进制随机数作为小车一维运动运动一次的指令，其中前10 位控制小车转向的角度，后10 位控制小车每次所走的路程。小车转向角度与控制位的关系：

1.5 小车位置的测量

（1）超声波反射法测量小车位置（一维）。测量一维运动中小车位置的方法如图3 所示。

图3 超声波反射法测量小车位置

将超声波发射／接收模块置于小车前端，通过式（8）计算小车距离前方挡板的距离即可推断出小车现在所处位置，数据通过蓝牙传送给电脑端进行分析处理。

式中：tEcho为超声波从发射到接收过程的时间；vsound为超声波在空气中的传播速度。

（2）梯形校正法测量小车位置（二维）。测量小车在二维平面内运动位置的方法为梯形校正法，如图4 所示。

图4 梯形校正法测量小车位置

利用插值算法对图片进行逐行扫描和插值，以使得图像视觉对齐。通过读取校正后小车的位置，软件可以较为准确地计算出小车在地面实际位置［15］。

2 实验方法

2.1 小波法生成随机数

为避免外界环境对提取噪声准确度的影响，用相机拍摄单一颜色的环境得到原始图像。如1.2、1.3 节所述，将原始图像灰度化，利用小波法生成噪声图像，取出每个像素点的灰度值生成二维矩阵，将此二维矩阵进行4 ×4 网格化处理，生成新的噪声图像，取出每个像素点的灰度值并将其灰度值数据转换为二进制随机数。

2.2 小车模拟粒子运动

如1.4 节所述定义小车运动的方法，将从图像噪声中产生的随机数存入只读存储器（Read-Only Memory，ROM），通过FPGA 读取储存在ROM 中的随机数并控制小车运动，使小车走出单个粒子布朗运动的轨迹。

3 数据测量与理论验证

实验通过FPGA 驱动小车运动，利用Matlab 进行实现噪声的提取和处理以及对实验数据的统计和分析。实验用小车如图5 所示。

图5 实验所用小车

3.1 小车模拟一维粒子布朗运动

（1）实验装置如图6 所示。

图6 一维布朗运动模拟装置

（2）实验数据与分析。由于实验空间以及超声波模块测量距离的限制，小车单次行驶的最大距离设置为400 mm，在小车运动过程中，记录小车运动的第5、10、15、20 和25 次运动后的位置，进行100 次实验，算出平均值与平方平均值见表1，并画出平方平均值与运动时间的关系图，如图7 所示。

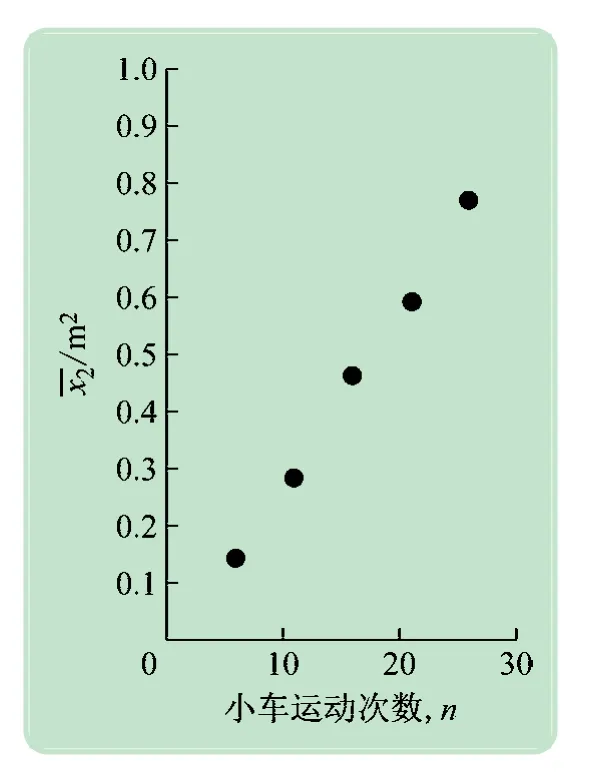
图7 均方位移与运动次数关系（一维布朗运动）

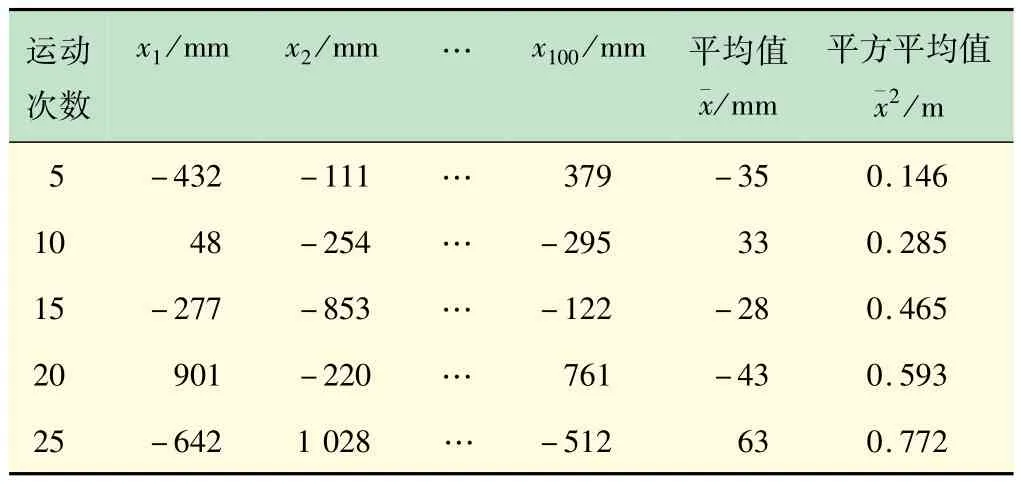
表1 一维布朗运动实验数据表（部分数据）

（3）一维单粒子布朗运动的仿真。因实验场地、小车电池电量等因素的限制，难以进行长时间的小车布朗运动的模拟，于是进行粒子一维布朗运动的仿真，并对布朗运动条件进行验证。

将粒子运动的最大距离归一化，规定每次实验粒子运动的次数为10，实验的次数n由10～10 000依次增加，计算n次实验中粒子的位移平均值，如图8（a）所示。可见，随着试验次数的增多，趋于0 附近，当粒子的平均数增加时，平均位移将稳定在原点附近，符合式（1）的布朗运动的规律。

将粒子运动的最大距离归一化，规定实验的次数n＝1 000，粒子每次实验运动的次数从1 依次增加到100，计算1 000 次实验中粒子分别运动1～100 次的位移的平方平均值2，如图8（b）所示。可见，位移的平方平均2风使舵与粒子的运动次数趋于成正比关系，粒子每次运动的时间是一定的，则粒子运动时间和运动步数成正比。由此，粒子运动的均方位移正比于运动时间，符合式（2）的布朗运动的规律。

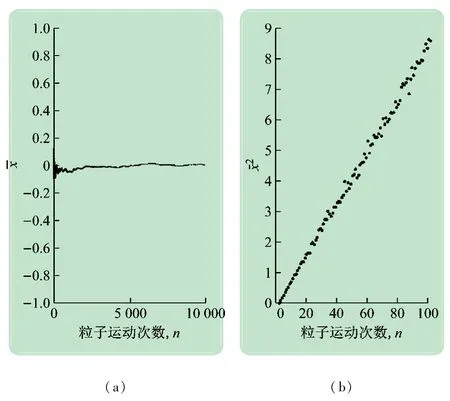
图8 一维布朗运动的仿真验证

3.2 小车模拟二维粒子布朗运动

（1）实验装置如图9 所示。

图9 二维布朗运动模拟装置

（2）实验数据与分析。小车单次行驶的最大距离设置为400 mm，在小车运动过程中，记录小车运动的第5、10、15、20 和25 次后的位置，进行100 次实验，算出平均值与平方平均值见表2，并绘制平方平均值与运动时间的关系图，如图10 所示。

图10 均方位移与运动次数关系（二维布朗运动）

表2 二维布朗运动实验数据表（部分数据）

4 实验误差分析

本实验是在宏观上对微观现象进行模拟，需要对模拟的准确度进行误差分析。误差主要来源于小车的转动惯性、与地面摩擦力的不均匀、小车电池电压不稳定等因素，还有在实验测量过程中的误差。在测量一维运动中，测量误差来自于超声波模块；在测量二维运动中，测量误差来源于梯形校正算法。

4.1 小车一维运动实验误差

设定距离为400 mm（单次运动的最大距离），记录超声波测距模块读出的测量距离见表3。

表3 小车一维运动实验误差测量数据表（部分数据）

根据表3 中L1和L2的数据以及超声波模块仪器手册读出的“Δ1＝0.1 mm”可算出不确定度为

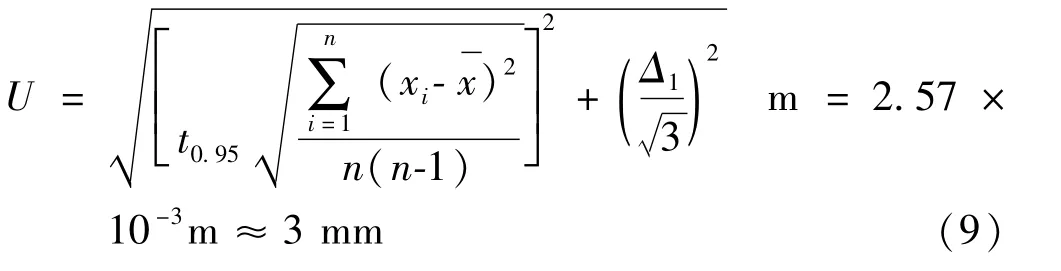
式中，n＝50。

在设定一维运动400 mm 的情况下，其测量距离为400 ±4 mm。

4.2 小车二维布朗运动实验误差

设定终点坐标为（400 mm，400 mm），用卷尺读出实际距离，用梯形校正法读出测量距离见表4。

表4 小车二维运动实验误差数据表（部分数据）

计算识别算法的误差“Δ2”：录像画面分辨率为1 920 ×1 080，每像素对应的实际长度约为0.15 mm，经过多次检验和边缘调整，小车识别点像素位置误差在x方向和y方向均不超过20 个像素点，即梯形校正后横、纵坐标测量误差均为8 mm，经计算可得Δ2＝3 mm。根据表4 中（x1，y1）和（x2，y2）的数据，算出不确定度分别为

式中，n＝50。

在设定二维运动目标坐标为（400 mm，400 mm）的情况下，其测量坐标为（400 ±9）、（400 ±9）mm。

5 结语

本实验通过图像噪声产生随机数，并用随机数控制小车作一、二维运动，作为微观布朗运动的宏观模拟。经Matlab仿真分析发现：小车运动的平均位移趋近于零，小车运动的均方位移和时间趋于正比关系，符合布朗运动的规律。通过本实验，将复杂和难以演示的微观粒子布朗运动，用简易的、易于展示的小车运动演示出来，对布朗运动的模拟展示具有一定的意义。