基于Maple的三铰斜拱力学分析及矢跨比优化

毛星波，盛冬发，朱 军

（西南林业大学土木工程学院，昆明 650224）

0 引言

中国作为基建大国，桥梁建设在促进国民经济发展和提高国民整体生活水平方面发挥了重大作用，拱桥作为一种历史悠久的桥梁结构在其中扮演着重要的角色。拱桥按受力体系可分为三铰拱、两铰拱和无铰拱，其中三铰拱因其良好的适用性与受力性能，在地势险峻偏远的地方得到广泛运用［1］。三铰拱实用理论的研究主要有力学分析与优化设计两个方面。在力学分析方面，李彤等［2-3］利用计算机编程求解三铰拱内力及其影响线，提高了三铰拱力学分析的精度与效率。夏健明［4］提出利用Excel数据计算及成图功能绘制三铰拱内力图，为三铰拱内力计算提供了一种新思路。也有学者对三铰拱的内力计算方法进行了研究［5-6］，或以现代流行语言为三铰拱内力计算编制相应程序［7-8］。在优化方面，任治章等［9-10］在合理拱轴线的基础上，推导出均布荷载作用下的三铰拱最优矢跨比理论解。邓小康等［11］基于拱圈自重建立微分平衡方程，解得了等截面空腹式三铰拱合理拱轴线。

上述研究的具体对象皆为三铰平拱，即两拱脚处于同一水平高度的三铰拱，对斜拱方面的研究则甚少。本文对三铰斜拱一些受力及优化的问题进行分析研究。首先，对竖向均布荷载下三铰斜拱的合理拱轴线分析求解，并对三铰斜拱约束反力及内力影响线函数进行推导；其次，建立以内力为目标函数的三铰斜拱矢跨比优化模型；最后，为便于本文理论在实际工程中的应用，使用Maple符号计算软件编制相应的计算程序，并通过案例验证文中理论推导的正确性及优化模型的优化效果。

1 三铰斜拱合理拱轴线分析求解

以拱的任一截面左边（或右边）所有外力的合力（包括数量、方向和作用点）作出合力多边形，该合力多边形称为拱的压力线。当拱的压力线与拱的轴线重合时，各截面的弯矩为零，拱处于无弯矩状态，这时各截面只受轴力作用。此时，使拱处于无弯矩状态的这一轴线称为合理拱轴线［12］。由此可知，拥有合理拱轴线的拱桥截面上应力均匀，能充分利用材料强度和圬工材料良好的抗压性能。

根据合理拱轴线定义，若使三铰斜拱的截面弯矩方程恒等于零，便有可能解出合理拱轴线函数。设三铰斜拱在均布荷载作用下截面弯矩恒等于零，其具体受力情况如图1 所示。

图1 三铰斜拱合理拱轴线推导简图

故有其任意截面的弯矩方程式

根据图1，建立B、C铰点的弯矩平衡方程组，以此解得A铰点支座水平反力FAx和A铰点支座垂直反力FAy。将FAx与FAy代回式（1），得其合理拱轴线式

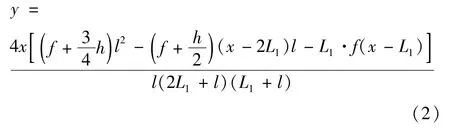
将A、B铰点拱脚高差h＝0、左右半拱跨长差L1＝0 代入式（2）得：

为三铰平拱在均布荷载作用下的合理拱轴线表达式［13-14］，表明式（2）对三铰平拱同样适用。

2 三铰斜拱影响线函数推导及内力计算

当一个指向不变的单位集中荷载（通常是竖直向下的）沿结构移动时，表示结构某一指定量值变化规律的图形，称为该量值的影响线［15］。在拱桥设计时，利用影响线确定拱桥关键截面上某量值的最不利荷载作用位置，并据此求出该量值在设计荷载作用下产生的最大值，以此作为关键截面尺寸和形状设计的依据。因此影响线的确定对拱桥设计至关重要。设三铰斜拱在单位竖向移动载荷FP作用如图2 所示，可分别推导支座垂直反力FAy、FBy，支座水平反力FAx、FBx，弯矩MK、剪力QK和轴力NK的影响线函数。

图2 三铰斜拱受力计算简图

2.1 支座反力影响线的推导

三铰斜拱与双铰拱、无铰拱具有明显不同的特征。双铰拱、无铰拱由于多余约束的存在为超静定结构，而三铰斜拱解除了多余约束，为静定结构。鉴于此，使用平衡方程可求解三铰斜拱支座反力影响线函数。另考虑到单位荷载的移动性，将支座约束反力影响线的求解分为单位荷载在左半拱时和右半拱时两种情况。依据图2 建立B、C铰点弯矩平衡方程组，求解出三铰斜拱A铰点支座反力影响线函数如下：

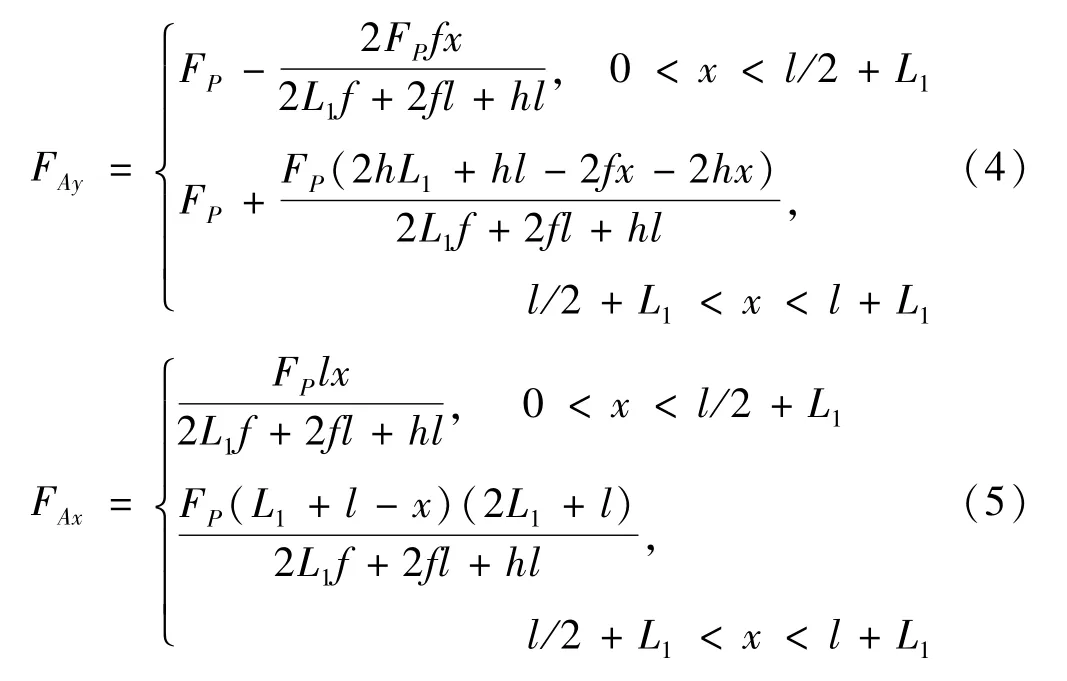
同理，建立A、C铰点弯矩平衡方程组，可求解出三铰斜拱B铰点支座反力FBy、FBx影响线函数。

2.2 内力影响线的推导

拱轴截面内力影响线可用截面法求得。左半拱截面的内力影响线计算简图见图3。图中：xK、yK为拟求解影响线的截面的形心坐标；φK为该截面处拱轴线倾角，可由拱轴线方程求导得出，其在右半拱时取值为负。另外，图3 中内力MK、QK、NK所示方向皆设定为正方向。根据图3，利用截面法对拟求解截面xK位于左半拱时的内力影响线函数进行推导，得内力MK、QK、NK影响线函数如下：

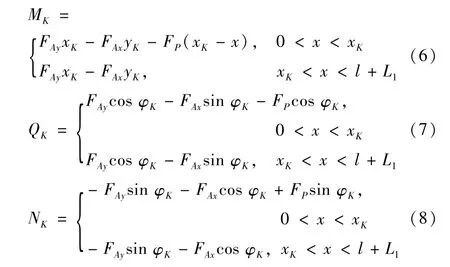
图3 左半拱内力影响线计算简图

同理，通过已知具体表达式的FBx、FBy影响线，可建立起拟求解截面xK位于右半拱时的内力影响线函数表达式。

2.3 三铰斜拱内力计算

因影响线描述了单位移动载荷作用下某量值的变化规律，故当荷载为集中荷载组或分布荷载组时，这些量值可以根据叠加原理利用影响线求得。考虑利用影响线计算三铰斜拱相关截面内力，其计算公式为

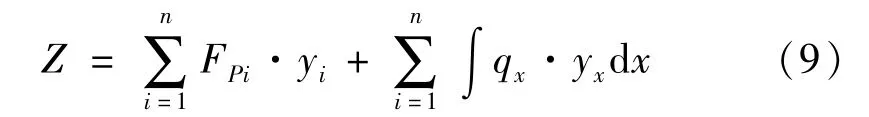
式中：Z为三铰斜拱因荷载作用所产生的量值大小，文中为指定截面弯矩MK、剪力QK、轴力NK的大小；FPi为若干竖向集中荷载；yi为与集中荷载相对应的影响线纵标；qx为分布荷载函数；yx为分布荷载相对应的影响线函数。

3 三铰斜拱矢跨比优化

虽然具有合理拱轴线形的拱桥截面应力均匀，能充分利用材料强度，但实际上拱桥不可能仅受均布载荷作用。此时，式（2）的合理拱轴线函数将变得不再那么“合理”，拱桥截面上也不再只有轴力。为使这种情况下的三铰斜拱受力更合理，考虑以拱轴各控制点内力平方和为目标函数对其进行矢跨比优化。所建立的矢跨比优化模型如下：

式中：设计变量f为矢高，其上下限值分别为fmax与fmin；Zi为各拱轴控制点处弯矩或轴力，其值大小用含矢高f的函数表示，具体表达式也可通过三铰斜拱Maple程序快速求得。各拱轴控制点的选取依据以下原则：若以弯矩为目标函数，则以集中力作用点、均布力作用范围起始点、均布力作用范围结束点、拱跨等分点为各控制点优先选择，其尽可能在拱轴线上均匀分布；若以轴力为目标函数，则优先将拱脚、拱顶选作为控制点，然后参考以弯矩为目标函数的选择方法选择其他控制点。得到优化模型具体表达式后，可利用数学计算软件对设计变量进行寻优，得到最优矢高。

4 三铰斜拱影响线绘制及内力计算的Maple编程

为便于工程实际应用，考虑将文中理论与方法编制成Maple程序，Maple软件提供的如符号计算、数值处理、二维与三维作图等广泛的数学计算功能得到了大量工程师及学者的青睐与使用［16］，故其也是目前世界上最为通用的数学和工程计算软件之一。Maple 程序编制的流程如图4 所示（具体代码可联系作者获知）。图中，拱形已知条件为三铰斜拱矢高f、跨长L、两拱脚高差h、左右半拱跨度差L1及拟求解影响线函数的截面的横坐标，荷载已知条件对于集中荷载，为其载荷作用点横坐标及载荷大小，对于分布荷载，为其载荷作用范围起始点、终止点及载荷函数。以上两已知条件皆由使用者根据工程实际情况输入。

图4 Maple程序运行流程

5 计算案例与验证

通过下面案例验证本文三铰斜拱力学推导的正确性及优化模型的优化效果。现已知有三铰斜拱如图5所示，其中拱脚高差h＝2 m、f＝4 m、L1＝2 m、l＝12 m。拱圈自重为均布荷载q＝58 kN／m，拱上车辆集中荷载FP1＝70 kN、FP2＝100 kN、FP3＝30 kN，其作用点横坐标分别为：x＝2 m，x＝6 m，x＝10 m。另外，该三铰斜拱设计矢高上下限为3.5～4.5 m，且x＝6 m 截面处为关键控制截面K截面。

图5 三铰斜拱案例

将案例拱形已知条件及拱圈自重荷载代入Maple程序，得到该三铰斜拱均布自重作用下的各截面内力。将上述内力数据与SAP2000 有限元内力分析结果进行对比，得到图6。从图6（a）、（b）知，SAP2000 和Maple对截面剪力及弯矩的分析结果都趋近于0。由此推断，本文给出的三铰斜拱合理拱轴线函数是正确的。另外，从图6（c）可以看出两者对于轴力的计算结果基本吻合，表明本文Maple 程序对案例截面内力的计算有较好的精度。

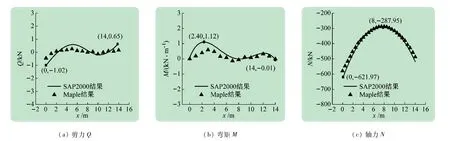
图6 均布自重作用下SAP2000和Maple求解内力对比

使用Maple程序与SAP2000 软件分别对该案例A铰点支座反力及K截面影响线进行分析及绘制，得到图7、8。图7 中，折线图为Maple 程序分析所得结果，其下方为SAP2000 软件分析结果。图8 布置与图7 相同，需注意的是，Maple 分析时设定的剪力正方向与SAP2000 软件相反。观察两图，图中两种方法所得的影响线的变化趋势及极值点特征基本一致。由此可推断，本文对三铰斜拱支座反力及内力影响线函数方程的推导也是正确的。

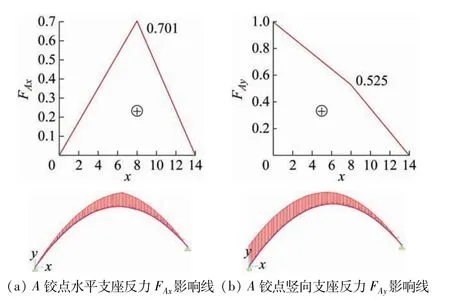
图7 A铰点支座反力影响线

图8 K截面内力影响线

对案例进行矢跨比优化。选取x＝0、2、6、8、10、14 m处截面作控制点，结合所给矢高约束条件，建立以轴力为目标的矢跨比优化模型。通过Maple程序得到优化模型具体表达式，并经数学计算软件寻优，得到优化矢高f为4.5 m，故其最佳矢跨比为9／28。优化前后的案例截面轴力对比见图9。由图9 知，优化后各截面轴力均有所减小，减小最大位置x＝6.5 m 处，减小了9.05%。以上结果说明，本文所提出的矢跨比优化模型取得了较好的优化效果。

图9 案例轴力N优化前后对比

6 结论

本文根据三铰斜拱受力特点，对其处于均布荷载下的合理拱轴线及相关影响线函数进行了推导，并以拱轴各控制点内力平方和为目标函数提出了一种矢跨比优化模型，最后编制了与文中理论相对应的Maple程序，得到的主要结论如下：

（1）推导得到了三铰斜拱合理拱轴线、支座反力及内力影响线函数表达式，对三铰斜拱的设计与建设有一定指导意义。其函数对于三铰平拱同样适用，统一了三铰拱受力计算公式。

（2）通过案例证明了文中矢跨比优化模型有较好优化效果，为三铰斜拱的矢跨比优化提供了明确且可行的理论支持。

（3）编制的Maple 程序为三铰斜拱支座反力、弯矩、剪力、轴力影响线的绘制及截面内力的计算提供了便利。同时，因程序中使用的函数对三铰平拱同样适用，故该程序也可用于三铰平拱相应问题的计算。